Некоторые символы математического языка — урок. Алгебра, 8 класс.
Натуральные числа — это числа, используемые для счёта предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
Множество всех натуральных чисел обычно обозначают буквой ℕ.Если к натуральным числам присоединить число \(0\) и все целые отрицательные числа: \(-1, -2, -3, -4…\) — то получится множество целых чисел. Это множество обычно обозначают буквой ℤ.
Если к множеству целых чисел присоединить все обыкновенные дроби: 13,5152,−85… и т. д. — то получится множество рациональных чисел. Это множество обычно обозначают буквой ℚ.
Множество ℚ рациональных чисел — это множество, состоящее из чисел вида mn;−mn (где \(m\), \(n\) — натуральные числа) и числа \(0\).
Понятно, что ℕ — часть множества ℤ, а ℤ — часть множества ℚ.
Для описания этой ситуации в математике также имеется специальное обозначение: ℕ⊂ℤ;ℤ⊂ℚ.
Математический символ ⊂ называют знаком включения (одного множества в другое).
Запись x∈X означает, что \(x\) — один из элементов множества \(X\).
А запись A⊂B означает, что множество \(A\) представляет собой часть множества \(B\). Математики чаще говорят так: \(A\) — подмножество множества \(B\).
Для записи, что элемент \(x\) не принадлежит множеству \(X\) или что множество \(A\) не является частью (подмножеством) множества \(B\), используют те же символы, но перечёркнутые косой чертой: x∉X,A⊄B.
Приведём несколько примеров использования введённых математических символов для сокращения записи верных математических утверждений — их называют также истинными высказываниями.
Пример:
7∈ℕ;7∈ℤ;7∈ℚ;−5∉ℕ;ℕ⊂ℚ;ℤ⊄ℕ;2∈1;6;1;3⊂−2;8.
Любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби:
722=0,3181818…=0,3(18);4=4,000…=4,(0);7,3777=7,37770000…=7,3777(0).
Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. Это значит, что любая бесконечная десятичная периодическая дробь есть рациональное число.
Переведём бесконечную десятичную периодическую дробь 4,5(28) в обыкновенную дробь.
Положим \(x=\) 4,5(28), т. е. \(x=\) 4,5282828… и т.д.
Умножим \(x\) на такое число,чтобы запятая передвинулась вправо до периода. Между запятой в числе \(x\) и началом периода стоит одна цифра, значит, запятую нужно передвинуть на одну цифру, т.е. умножаем \(x\) на \(10\). Получим 10x=45,282828… и т.д.
Теперь умножим \(x\) на такое число,чтобы запятая стояла после периода.
Поскольку в нашем случае после запятой и до периода стоит одна цифра, в периоде содержатся две цифры, нужно, чтобы запятая передвинулась вправо на три цифры. Для этого число \(x\) надо умножить на 1000. Получим 1000x=4528,282828… и т.д.
Вычтем из второго равенства первое равенство.
1000x=4528,282828…10x=45,282828…
990x=4483¯
Отсюда x=4483990=4523990.
Приведём примеры перевода бесконечной десятичной периодической дроби в обыкновенную в сокращённой записи.
Пример:
1,(23)=123−199=12299=12399;1,5(23)=1523−5990=1518990=1259495.
Откуда взялись плюс и минус?
На этот раз любопытные Кубик и Шарик решили выяснить, когда человечество стало использовать плюсы и минусы. Кажется, они были всегда…или нет?
– Шарик, расскажи, со знаками действий все же просто, да? Вот в Древнем Египте, как мне говорили, египтяне уже писали плюс и минус!
– Почти, Кубик.
Смотри, в древнем Египте был иероглиф , которым обозначали сложение и вычитание. Согласно некоторым источникам, это был специальный знак, используемый только в математике. Действительно, в Московском папирусе есть такие знаки. Поскольку египтяне писали и справа налево, и слева направо, то этот символ означал и “прибавить” и “отнять” – в зависимости от направления текста .
– А что такое Московский папирус?
– Московский папирус – это один из двух египетских математических папирусов, дошедших до наших дней. Он составлен примерно в 1850 году до нашей эры и считается одним из древнейших математических текстов. Посмотри внимательно! Видишь, там есть ноги? Значит, что-то складывали или вычитали.
То, что ты видишь, не совсем настоящий папирус. Это специальный текст, переведенный учеными на белый лист, чтобы было легче расшифровывать и изучать его.
– Слушай, Шарик, а почему этот папирус “Московский”? Его что, в Москве нашли? Вот это да!
– Нет, Кубик, нашел его в Египте один из основателей русской египтологии Владимир Голенищев.
А вот хранится “папирус Голенищева” в Москве, да не где-нибудь, а в Музее изобразительных искусств им. А. С. Пушкина. Ты его наверняка знаешь как “Пушкинский музей”.
– Теперь понятно. А что там с ногами?
– Ученые-египтологи тщательно расшифровывали и изучали папирус, и пришли к выводу, что эти знаки не были аналогами знаков “плюс” и “минус”, а были словами “добавить” и “отнять”. И в других, нематематических текстах они тоже встречаются.
– Наверное, дело в том, что в древние времена математика была практической дисциплиной, использовалась в основном для расчетов между людьми. Получается, абстрактные понятия и знаки были не нужны.
– Точно, Кубик. Ну что ж, символ есть, но это не знак, а слово…
– А я думал, мы уже все нашли и расследовали, а оказывается… Все начинать сначала! Где у нас там еще математикой занимались?
– Давай отправимся к шумерам, в Междуречье. До нас дошло огромное количество глиняных табличек, в том числе с математическими расчетами.
Вот, например, таблица умножения: таких табличек найдено очень много, а часть из них с ошибками. Есть предположение, что таблицу умножения изучали в школах.
Каждая строчка начинается со слова “умножить”.
– Шарик, ну вот же, мы нашли! Вот же оно, обозначение умножения, сложения, вычитания…
– Дорогой Кубик, ты снова путаешь! Для нас сегодняшних это выглядит, как знаки, но на самом деле это не математические знаки, а слова!
– умножить, – отнять, – сложить.
Есть множество табличек, где ученые только по числам догадываются, что же делали с числами, то есть знаки действий не обозначались никак. Математика – это очень практическая дисциплина, она служила бытовым и религиозным целям. Абстрактных понятий пока еще нет, значит, и специальных знаков не нужно.
– Ну надо же! Раз в Месопотамии знаков нет, значит, и в Древней Греции их тоже нет?
– Не совсем так, Кубик. Древнегреческая цивилизация была первой, где создавались философские школы и изучались науки не с практической, а с исследовательской, научной целью.
– Папирусов? Ты хочешь сказать, что и в Греции писали на папирусе?
– Конечно, потому что это был дешевый и легкий в изготовлении материал, очень удобный. Его использовали в средиземноморье вплоть до 12 века, пока он не был вытеснен бумагой.
Но вернемся к математике. В 3 веке до нашей эры, в Александрии, жил величайший математик Евклид. Он оставил огромный труд “Στοιχεῖα ” – “Начала” , или в английской традиции “Элементы”, которым, как учебником по геометрии, пользовались до середины 19 века. Сохранились несколько оригинальных листов, и многочисленные переводы на латинский и английский. Посмотри, вот греческий текст и перевод на английский, все описывается словами.
Чуть позднее, в работах Диофанта во 2 веке до нашей эры, появляются первые абстрактные символы, обозначающие возведение в степень и вычитание, а также символы для обозначения отрицательных чисел.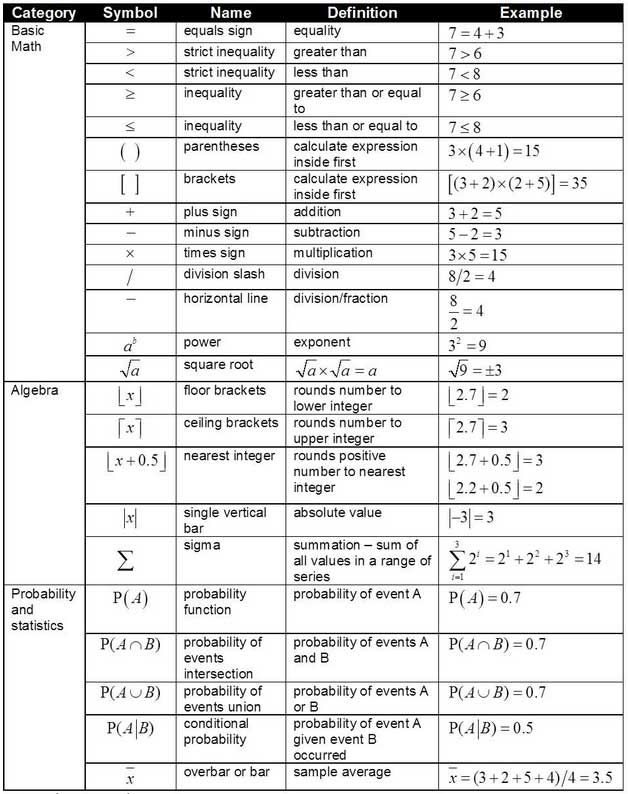
– Эврика! Нашли! Вот же они, первые математические символы!
– Да, Шарик, ты прав, это именно символы, не слова, но, увы, они остались только в книгах Диофанта и не были использованы другими математиками. Более того, каждая математическая школа придумывала свои символы или описывала действия словами. Никакой стройной системы не было.
– Как же так? Почему?
– Людей разделяли расстояния, войны и языки, одни философские школы и ученые не знали, что делается в других. Так продолжалось довольно долго, необходимость использовать символы вместо слов была, но единой записи пока не было. Самое удивительное, что аж до 15 века все действия даже в научных работах по-прежнему описывались словами или символами, используемыми только одним ученым.
Поскольку в те времена большинство научных книг писалось и издавалось на латыни, а все математические действия записывали словами, было не сразу понятно, что книга на самом деле посвящена математике.
– Вот бы их удивили наши учебники! Мало того, что везде какие-то непонятные знаки, так еще и язык не тот. Постой, Шарик, так кто же все-таки придумал плюс и минус?
– В 1417 году выходит “Книга о небе и мире” Николая Орема, в которой для обозначения сложения используется знак +. Поскольку книга была рукописная, то, скорее всего, это было сокращенное написание et, от которого осталась лишь буква t, похожая на привычный нам знак сложения. Писали, например, “4 et 5” , что в переводе с латинского означало “4 и 5”. До изобретения первого печатного станка оставалось еще почти 40 лет, поэтому записи легко могли сокращаться и писаться любыми символами, удобными автору.
– И что, вот теперь уже во всех книгах используют знак +?
– Нет, Кубик, информация в те времена распространялась медленно, и использование знака в одной книге не означало, что это увидели другие ученые. Некоторые из них использовали другие сокращения, которые им казались логичными и понятными.
– Шарик, я помню, что первая библия была напечатана Гутенбергом в 1455 году. Значит, после этого книги уже печатались, а не переписывались?
“Быстрый и наглядный счет для торговцев” Видмана– Не совсем так, но довольно быстро этим величайшим изобретением стали пользоваться. Книги, безусловно, стали доступнее. В 1489 году немецкий математик Иоганн Видман публикует (именно публикует и довольно большим тиражом) книгу “Быстрый и наглядный счет для торговцев”, где впервые появляется привычная для нас запись арифметических действий. Однако в этой книге + и – обозначали еще не знаки действий, а дебиторскую и кредиторскую задолженность.
Но это была уже печатная книга, доступная по цене не только ценителям книг, но и торговцам, для которых она и писалась. Получается, об этой удобной записи могли узнать многие! В 1518 году в Германии издается книга Генриха Грамматеуса, где + и – уже используются для арифметических действий.
– Ну вот же! Смотри, уже и арабские цифры, и плюсы, и минусы, все уже выглядит привычно! Но где же знак “равно”?
– До его появления еще почти 40 лет, но помнишь, в древности почти ничего не менялось за 300 лет, а тут все стремительно меняется.
– Да уж, прошло всего-то сто лет с печати первой книги!
– Правильно! В 1557 году выходит книга Роберта Рекорда, валлийского математика и врача, преподавателя Оксфорда, где он впервые использует одновременно плюс и минус, а также в первый раз использует знак равенства.
Книга Рекорда– Вот она, привычная нам запись! Знаки выглядят большими, но даже я могу разобрать, что там написано.
– Не только тебе понравилась такая запись, она довольно быстро распространилась среди ученого мира и стала общепринятой.
Вот такая непростая история у привычной нам записи математических действий. А вот знаки “умножить” и “разделить” даже сейчас в школах разных стран записывают по-разному!
Презентация по математике:»История символов»
Скрыть
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:История символов.
Что такое символ? Символ – это знак. Он используется для компактной записи математических уравнений и формул. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского), математический язык использует множество специальных символов, изобретённых за последние несколько столетий.
3 слайд Описание слайда:Десятичная запятая Десятичная запятая, отделяющая дробную часть числа от целой, введена итальянским астрономом Маджини (1592). Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62; некоторые авторы, следуя ал-Каши, употребляли чернила разного цвета. В Англии вместо запятой предпочли использовать точку, которую ставили посередине строки; эту традицию переняли в США, однако сдвинули точку вниз, чтобы не путать её со знаком умножения.
Знак умножения Знак умножения ввёл в 1631 году Уильям Отред в виде косого крестика. До него использовали чаще всего букву M, хотя предлагались и другие обозначения. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x.
5 слайд Описание слайда:Знаки деления Уильям Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также горизонтальная черта дроби, употреблявшаяся ещё у Герона, Диофанта и в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложил Иоганн Ран в 1659 году.
6 слайд Описание слайда: Уи́льям О́тред — английский математик.
В старых русских источниках может называться Вильям Отред или Вильям Оутред. Известен как изобретатель логарифмической линейки и один из создателей современной математической символики. Труды Отреда оказали значительное влияние на развитие алгебры.
Дробная черта «Двухэтажная» запись обыкновенной дроби использовалась ещё древнегреческими математиками, хотя знаменатель у них записывался над числителем, а черты дроби не было. Индийские математики переместили числитель наверх; через арабов этот формат переняли в Европе. Дробную черту впервые в Европе ввёл Леонардо Пизанский (1202), но в обиход она вошла только при поддержке Иоганна Видмана (1489).
8 слайд Описание слайда:Знаки плюс и минус Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов).
Они используются в учебнике Иоганна Видмана «Быстрый и приятный счёт для всех торговцев», изданном в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
Возведение в степень Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели, трактовку которых к этому времени уже предложили Стевин, Валлис и Жирар.
10 слайд Описание слайда:Квадратный корень Средневековые математики (например, Кардано) обозначали квадратный корень символом R или стилизованной комбинацией R_x (от лат.
Radix, корень). Современное обозначение знака корня впервые употребил немецкий математик Кристоф Рудольф, в 1525 году. Происходит этот символ от стилизованной первой буквы того же слова radix. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт (1637) для иной цели, и эта черта вскоре слилась со знаком корня.
Знак равенства Знак равенства предложил Роберт Рекорд в 1557 году; начертание символа было намного длиннее нынешнего. Автор пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. Некоторое время распространению символа Рекорда мешало то обстоятельство, что с античных времён такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным.
12 слайд Описание слайда:Символ процента Символ процента появляется в середине XVII века сразу в нескольких источниках, его происхождение неясно.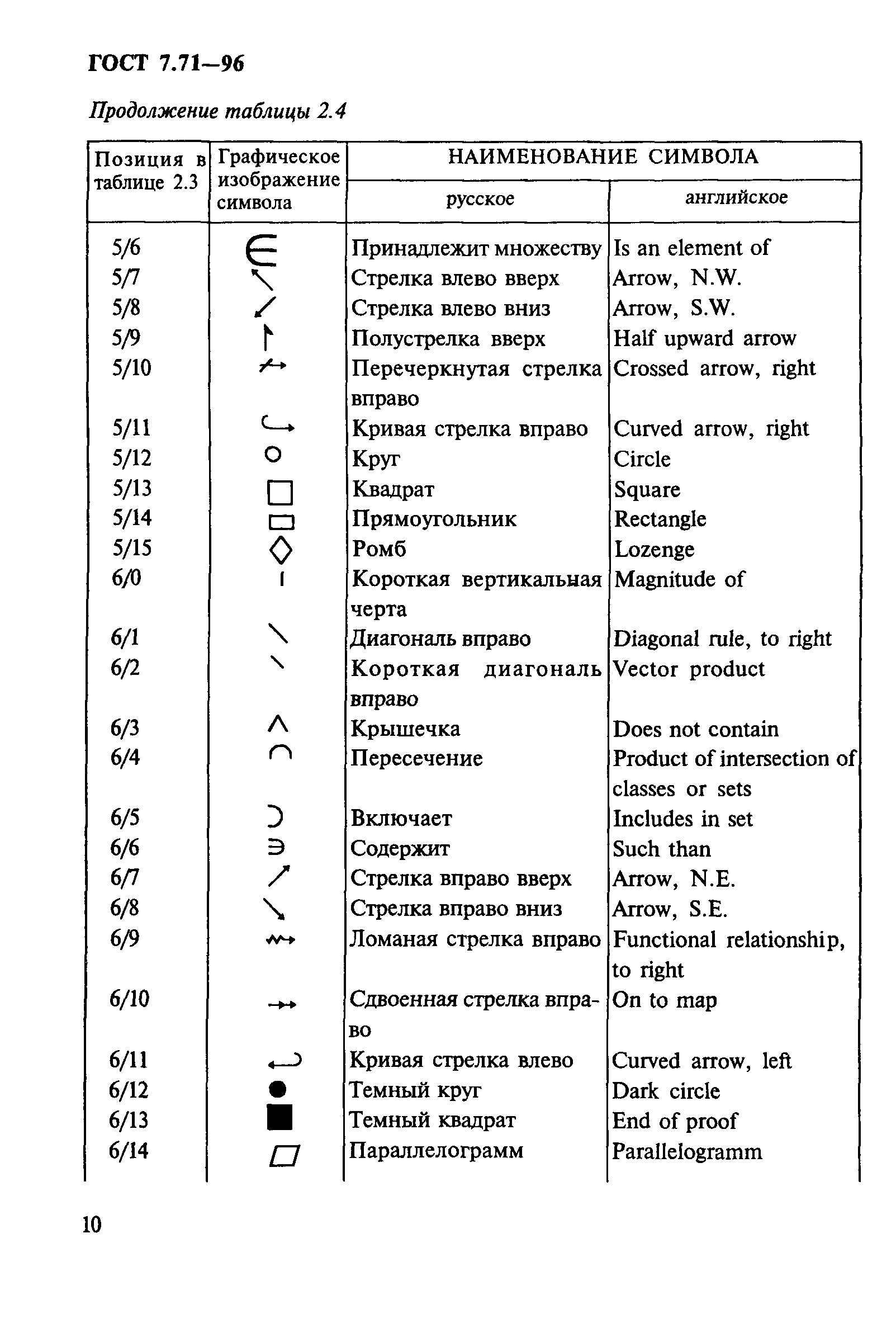
Есть гипотеза, что он возник от ошибки наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более вероятно, что это скорописный коммерческий значок, возникший лет на 100 раньше.
Знак интеграла Знак интеграла используется для обозначения интеграла в математике. Впервые он был использован немецким математиком и основателем дифференциального и интегрального исчислений Лейбницем в конце XVII века. Символ (∫) образовался из буквы ſ («длинная s»; от лат. ſumma (summa) — сумма).
14 слайд Описание слайда: Го́тфрид Ви́льгельм Ле́йбниц- немецкий философ, логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук.
Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон. Символ бесконечности придумал Валлис, опубликован в 1655 году.
16 слайд Описание слайда:Арабские цифры Написание арабских цифр состояло из отрезков прямых линий, где количество углов соответствовало величине знака. Вероятно, кто-то из древних математиков когда-то предложил идею — связать числовое значение цифры с количеством углов в ее начертании.
17 слайд Описание слайда: 0 — цифра без единого угла в начертании 1 — содержит один острый угол 2 — содержит два острых угла 3 — содержит три острых угла 4 — либо содержит 4 прямых угла, либо два прямых и два острых 5 — содержит 5 прямых углов 6 — содержит 6 прямых углов 7 — содержит 7 прямых и острых углов (правильное, арабское, написание цифры 7 отличается наличием дефиса, пересекающего вертикальную линию посередине) 8 — содержит 8 прямых углов, либо 6 острых и 2 тупых 9 — содержит 9 прямых углов (именно этим объясняется столь замысловатый нижний хвостик у девятки, который должен был достроить аж 3 угла, чтобы общее их число стало равно 9.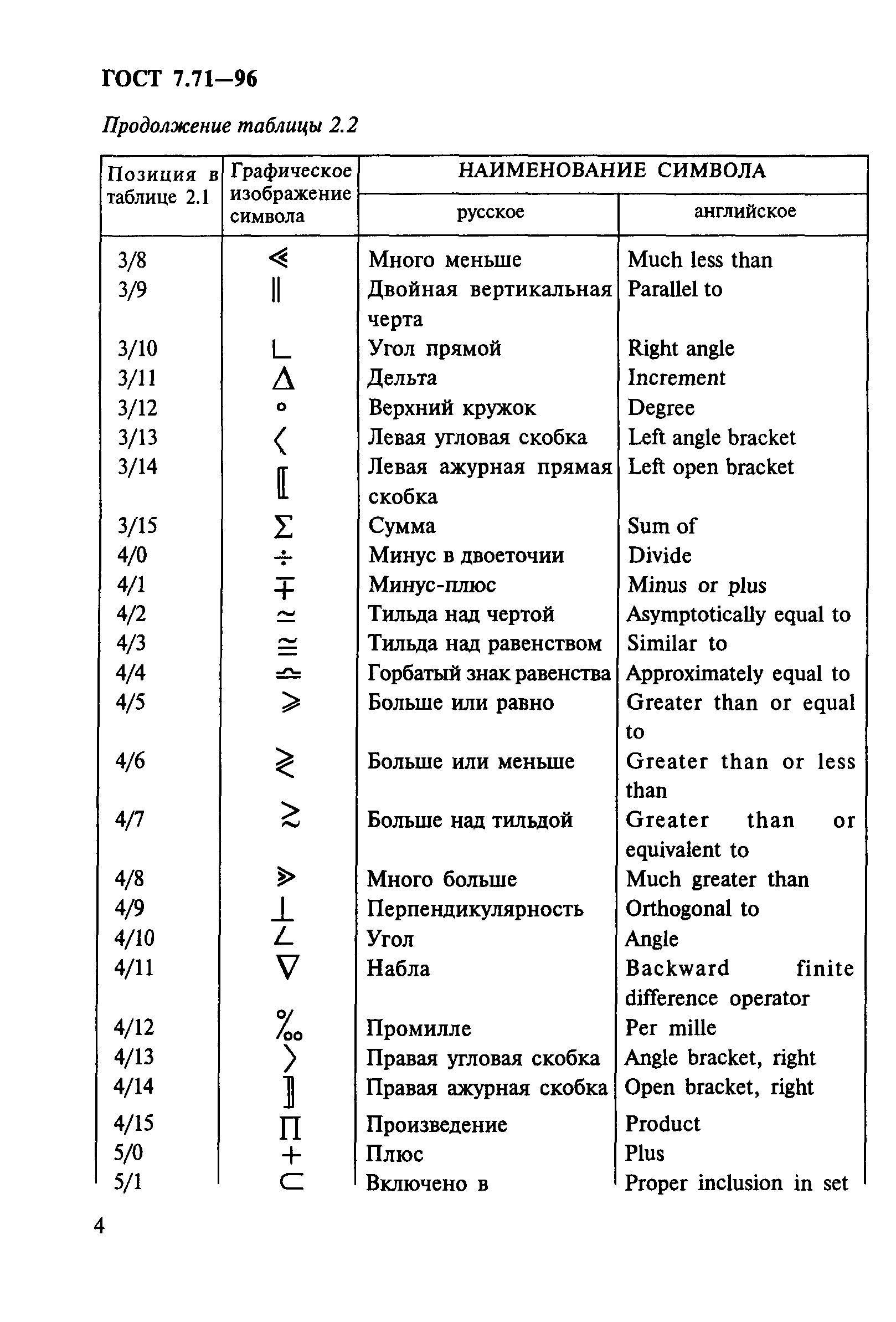
https://ru.wikipedia.org/wiki/%D0%9E%D1%82%D1%80%D0%B5%D0%B4,_%D0%A3%D0%B8%D0%BB%D1%8C%D1%8F%D0%BC http://pozitivno.in.ua/proisxozhdenie-arabskix-cifr/
19 слайд Описание слайда:Автор презентации: ученица 8 класса Хорошилова Екатерина.
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель математики
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп.
образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-403851
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике.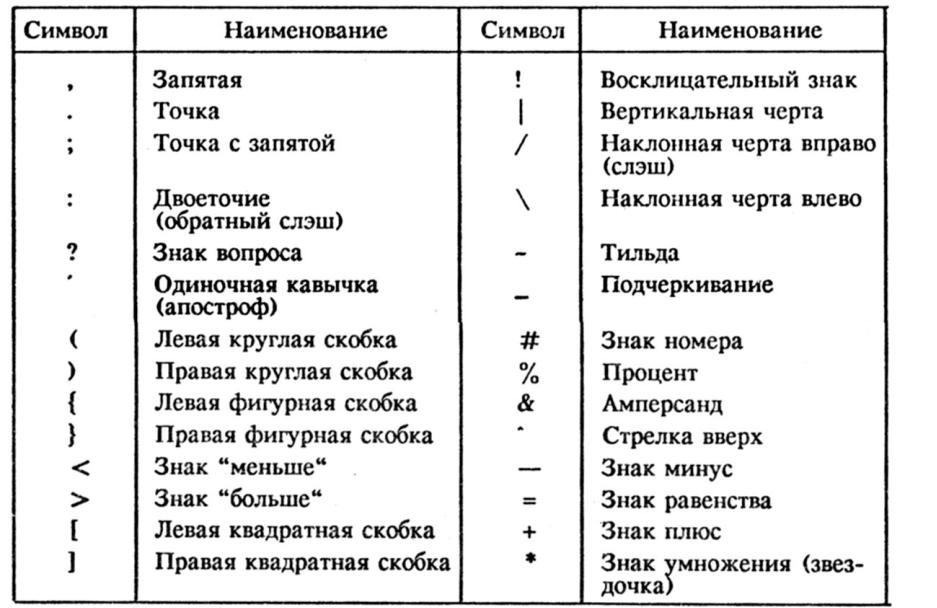
Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел.
Если мы умножаем «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Правила при умножении (делении) чисел | |||||||||||||||
| |||||||||||||||
Двойные математические знаки.
Необходимы ли они? : Пургаторий (М)FD.039Я не предлагаю знак двойного деления. Я предлагаю знак на замену вашей дробной черты. Чтобы писать в вашем духе
За предложение – благодарю. Но смысл введения двойного знака деления не в том, чтобы заменить дробную черту, а в том, чтобы обозначить вполне определенную математическую операцию – сокращение дроби (отношения). Для которого специального знака не было и мне его пришлось ввести.
В вашей записи народ будет путаться. Гораздо лучше, если так: Или так:
Есть и преемственность с операцией просто деления дроби, и сразу видно, что не делить нужно ее, а сокращать. Не так ли?
— 18.09.2012, 17:43 —
FD.040
Двойной интеграл — это просто повторный, то есть не специальный знак, а два раза использованный обыкновенный знак интеграла. Никаких специальных «двойных знаков» в математике никто не вводил и не вводит.
Тем лучше! Значит, я буду первым, кто это сделает. Тем более что формулы в моей «Теории цены» без этих знаков записывать трудно.
Впрочем, тут особого приоритета нет. Потому что, ведь, я тоже не ввожу новых знаков, а, также, как и в случае с двойным интегралом, повторяю уже известные знаки. Для обозначения новой операции. Всего лишь. Так что новизна, объективно, – небольшая. Но она – есть.
Кстати, у вас насчет двойных знаков немного неточная инфа. Двойной знак умножения, скажем, вводился. Но не прямо в математике, а в ФОРТРАНЕ. Правда, он там используется как символ не деления, а возведения в степень. (См. 04.955 — http://universal_de_ru.academic.ru/6493 … onszeichen .)
ДП
Сегодня нашел это в Нете. Фортран изучал еще в институте, но это было давно, и, естественно, я об этом благополучно забыл. Увы!
— 18.09.2012, 18:24 —
FD.041. Выводы предварительные
Таким образом, пока результаты обсуждения необходимости введения двойных знаков основных математических действий можно представить в следующем виде:
1. Против введения этих знаков никто принципиально не выступает. Ибо очевидно: они нужны.
Для обозначения операций, которые объективно существуют, но не имели до сих пор своих знаков.
2. Двойные математические знаки вводились и ранее, но для элементарных математических действий с дробями (отношениями) нет. (Использовался только знак двойного интеграла и двойного умножения в Фортране.)
3. За самими знаками следует закрепить следующие обозначения и названия:
• ++ …………… Знак двойного суммирования (интегрирования, объединения отношений в одно целое).
• ** ……………. Знак «расширения» дроби (отношения).
• :: или // ……. Знак сокращения дроби или отношения.
Ученые назвали правильный ответ в спорном примере из школьного курса математики — Общество
МОСКВА, 1 августа. /Корр. ТАСС Олеся Кулинчик, Александра Рыжкова/. Правильный ответ в примере из школьной математики с делением и умножением, породившем споры в социальных сетях, — «16». Об этом ТАСС заявили известные российские математики.
28 июля один из пользователей опубликовал в Twitter пример из школьной программы по математике: «8:2(2+2)=?».
Обсуждение примера вызвало широкий резонанс, и перешло на международный уровень, пользователи разных стран получали ответ «16» или «1».
Российский математик, доктор физико-математических наук, первый декан факультета математики Высшей школы экономики Сергей Ландо рассказал ТАСС, что правильный ответ в России будет 16. «На территории Российской Федерации деление и умножение имеют равные приоритеты. В США или Англии может быть другой порядок. В России сначала выполняется операция в скобках, потом деление на эту сумму, а потом результат умножается на следующий множитель. Правильный ответ — 16», — сказал он. Ландо добавил, что в подобных спорных случаях специалисты стараются обозначить порядок операций скобками.
Заведующий кафедры высшей математики Национального исследовательского университета «Московский институт электронной техники» (НИУ МИЭТ) Александр Прокофьев подтвердил ТАСС, что правильный ответ — 16, и объяснил, почему пример вызвал столько споров.
«Ошибаются, как я полагаю, преимущественно взрослые.
У школьников вопросов быть не должно. Первой выполняется операция в скобках, затем, согласно приоритету арифметических действий, деление и умножение — они являются равноправными и выполняются слева направо. Студенты привыкают отделять косой чертой числитель от знаменателя, поэтому путаются в данном примере, полагая, что умножение двойки на скобку расположено в знаменателе», — сказал Прокофьев.
С ними согласилась и заведующая кафедры «Математика» Российского университета транспорта Людмила Кочнева. «Если бы стояла скобка после знака деление, то правильным ответом была бы единица. Если бы после восьмерки была горизонтальная черта — знак дробного деления — а внизу 2(2+2), это была бы единица. А раз все это в строчку, вы должны делать операции в том порядке, в котором они написаны. Восемь делим на два, четыре умножаем на 2+2, получается 16. Это просто манера записи, ничего интересного — чисто арифметическая задача, но все-таки более опрятно надо писать сам пример», — пояснила она.
1 класс, знаки плюс, минус, равно
Дата публикации: .
Урок и презентация на тему:
«Знаки арифметических действий: плюс, минус, равно»
Знаки: плюс, минус, равно
В стране математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними.
Посмотрите на рисунок. Сколько белочек на рисунке?
А теперь сколько белочек? На 2 белочки больше, правильно?
В математике это действие называется сложением и ставится знак плюс.
Вот как это выглядит:
4 белочки + 2 белочки:
А теперь запишем это действие цифрами:
Я – нужный знак, и я горжусь,
Что для сложения гожусь.
Я добрый знак соединения.
И в том мое предназначенье.
Всем людям честно помогаю!
Я СКЛАДЫВАЮ и ПРИБАВЛЯЮ!
Но в математике есть ещё один нужный знак. Давайте посмотрим, какой.
Посчитаем, сколько на рисунке белочек?
Но, 2 белочки убежали. Сколько белочек осталось?
В математике это действие называется вычитание и обозначается знаком минус.
А теперь запишем это действие цифрами:
Я – тоже очень нужный знак,
Но, только не пойму никак
Почему люблю всё отнимать,
Отнимать и вычитать.
Все, что хочу, я забираю!
Я ВЫЧИТАЮ! ВЫЧИТАЮ!
Скажите, дети, вы знаете, кто это так поёт? Правильно, это Я — Математический знак минус.
Вы с Лисёнком уже узнали, что в математике самые главные знаки: ПЛЮС и МИНУС. Но, есть ещё один очень важный знак. Давайте посмотрим, что это за знак.
Давайте снова вспомним наших белочек. Мы сначала прибавили, но не записали, сколько их всего.
Чтобы записать, сколько всего белочек, нам на выручку придёт ещё один важный знак. Называется он РАВНО и выглядит вот так.
Я самый дружный в мире знак.
Я всех всегда равняю.
Я всех всегда мирю,
Ни про кого не забываю
И всех люблю.
Вы с Лисёнком уже познакомились с важными знаками. Давайте посмотрим, как будут выглядеть наши примеры.
Решаем задачки и используем знаки: ПЛЮС, МИНУС, РАВНО
А теперь, помогите Лисёнку решить три весёлых задачки.
Сели у окошка.
Тут одна к ним прибежала.
Сколько вместе кошек стало?
Пять весёлых медвежат
За малиной в лес спешат.
А один вдруг испугался.
Дома на печи остался.
Сколько смелых медвежат
За малиною спешат?
Ёжик стал грибы искать.
Под берёзой было пять.
Под осиной три нашёл.
И домой скорей пошёл.
Сколько грибочков нашел Ёжик?
Сегодня вы с Лисёнком узнали самые важные математические знаки. Вспомните их.
Знак
(математика) — Простая английская Википедия, бесплатная энциклопедия
Знаки плюс и минус используются для обозначения знака числа. Плюс означает положительный, а минус означает отрицательный. В математике слово знак обозначает свойство быть положительным или отрицательным. Каждое действительное число, отличное от нуля, может быть положительным или отрицательным и, следовательно, имеет знак. Сам по себе ноль без знака или без знака.
Помимо добавления знаков к действительным числам, слово «знак» используется в математике для обозначения частей математических объектов, которые означают положительность и отрицательность.Обычно, если числа отображаются без знака, они рассматриваются как положительные числа. В противном случае перед числом добавляется знак минус «- {\ displaystyle -}», чтобы указать, что это число является отрицательным для другого числа. [1] [2]
Слово «знак» также иногда используется для обозначения различных математических знаков, таких как знаки плюс и минус и знак умножения.
Действительное число считается положительным, если оно больше нуля, и отрицательным, если оно меньше нуля.Признак положительности или отрицательности называется знаком числа. Сам по себе ноль не считается знаком. [3]
В арифметике знак числа часто обозначается помещением знака плюс или минус перед числом. Например, +3 будет обозначать положительное число 3, а −3 — отрицательное число 3.
Когда не указан знак плюс или минус, основной способ увидеть это число — это положительное число. [2]
Знак любого числа, отличного от нуля, можно изменить на положительный с помощью функции абсолютного значения.Например, абсолютное значение −3 и абсолютное значение 3 равны 3. В символах это будет записано как | −3 | = 3 и | 3 | = 3.
Знак нуля [изменить | изменить источник]
Число ноль не является ни положительным, ни отрицательным, и поэтому не имеет знака. [3] В арифметике +0 и -0 означают одно и то же число 0.
Поскольку ноль не является ни положительным, ни отрицательным, для обозначения знака неизвестного числа иногда используются следующие слова:
- Число положительное , если оно больше нуля.
- Число отрицательное , если оно меньше нуля.
- Число неотрицательное , если оно больше или равно нулю.
- Число неположительное , если оно меньше или равно нулю.
Таким образом, неотрицательное число может быть либо положительным, либо нулевым, а неположительное — отрицательным или нулем. Например, абсолютное значение действительного числа всегда неотрицательно, но не обязательно положительно.
То же определение иногда используется для функций, которые принимают действительные или целые значения.Например, функция будет называться положительной, если все ее значения положительны, или неотрицательными, если все ее значения неотрицательны.
Знак угла [изменить | изменить источник]
Во многих текстах часто встречается знак вместе с величиной угла, в частности, локализованный угол или угол поворота. В такой ситуации знак говорит, идет ли угол по часовой стрелке или против часовой стрелки. Хотя могут использоваться разные соглашения, в математике принято считать, что углы против часовой стрелки считаются положительными, а углы по часовой стрелке считаются отрицательными.
Также можно поставить знак угла поворота в трех измерениях, предполагая, что ось вращения ориентирована.
В частности, правый поворот вокруг оси обычно считается положительным, а левый — отрицательным.
Знак направления [изменить | изменить источник]
В арифметике и физике принято обозначать определенные направления как положительные или отрицательные. В качестве базового примера числовая линия обычно рисуется с положительными числами справа и отрицательными числами слева:
На декартовой плоскости правое и восходящее направления обычно считаются положительными, при этом вправо считается положительным направлением x , а вверх — положительным направлением y .
Другие значения [изменить | изменить источник]
Помимо знака действительного числа, слово «знак» также используется по-разному в математике и других науках:
- В теории графов граф со знаком — это граф, в котором каждое ребро помечено положительным или отрицательным знаком.
- В физике у любого электрического заряда есть знак, положительный или отрицательный. По общим правилам, положительный заряд — это заряд того же знака, что и протон, а отрицательный заряд — это заряд того же знака, что и у электрона.
По общим правилам, положительный заряд — это заряд того же знака, что и протон, а отрицательный заряд — это заряд того же знака, что и у электрона.- ↑ «Список арифметических и общих математических символов». Математическое хранилище . 2020-03-17. Проверено 26 августа 2020.
- ↑ 2,0 2,1 «Сложение и вычитание положительных и отрицательных чисел». www.mathsisfun.com . Проверено 26 августа 2020.
- ↑ 3,0 3,1 «Числа — целые числа со знаком — подробно». www.math.com . Проверено 26 августа 2020.
| Символ | Значение | Пример |
|---|---|---|
| + | добавить | 3 + 7 = 10 |
| – | вычесть | 5−2 = 3 |
| × | умножить | 4 × 3 = 12 |
| ÷ | делить | 20 ÷ 5 = 4 |
| / | делить | 20/5 = 4 |
| () | группировка символов | 2 (а-3) |
| [] | группировка символов | 2 [a − 3 (b + c)] |
| {} | набор символов | {1, 2, 3} |
| π | пи | А = πr 2 |
| ∞ | бесконечность | ∞ бесконечен |
| = | равно | 1 + 1 = 2 |
| примерно равно | π 3. 14 | |
| ≠ | не равно | π ≠ 2 |
| <≤ | меньше, меньше или равно | 2 <3 |
| > ≥ | больше, больше или равно | 5> 1 |
| квадратный корень («корень») | √4 = 2 | |
| ° | градусов | 20 ° |
| следовательно | a = b b = a |
Математические символы и их значение
Математические символы — часто крошечные, неразборчивые и кажущиеся случайными — очень важны.Некоторые математические символы представляют собой греческие и латинские буквы, восходящие к древним временам.
Другие, такие как знаки плюса, минуса, времени и деления, кажутся простыми обозначениями на бумаге. Тем не менее, символы в математике — это, по сути, инструкции, которыми руководствуются ученые в этой области. И они имеют настоящую ценность в реальной жизни.
Знак «плюс» (+) может сказать вам, добавляете ли вы наличные на свой банковский счет, а знак «минус» (-) может указывать на предстоящие проблемы — что вы вычитаете средства и, возможно, рискуете исчерпать деньги.Круглые скобки, которые в английской пунктуации указывают на то, что вы вставляете несущественную мысль в предложение, в математике означают прямо противоположное: сначала вы должны проработать то, что находится внутри этих двух знаков препинания, и только потом решать остальную задачу. Читайте дальше, чтобы узнать, что такое общие математические символы, что они представляют и почему они важны.
Общие математические символы
Вот список наиболее распространенных символов, используемых в математике.
Символ | Что представляет собой |
| + | Добавляющий знак: часто обозначается как знак плюса или сложения. |
| — | Знак вычитания: часто обозначается как знак минус |
| x | Знак умножения: часто упоминается как знак умножения или таблицы умножения. |
| ÷ | Знак деления: Разделить |
| = | Знак равенства |
| | | | Абсолютное значение |
| ≠ | Не равно |
| () | Круглая скобка |
| [] | Квадратные скобки |
| % | Знак процента: Из 100 |
| ∑ | Знак большой суммы: суммирование |
| √ | Знак квадратного корня |
| < | Знак неравенства: менее |
| > | Знак неравенства: больше |
| ! | Факториал |
| θ | Тета |
| π | Пи |
| ≅ | Примерно |
| ∅ | Пустой набор |
| ∠ | Угловой знак |
| ! | Факторный знак |
| ∴ | Следовательно |
| ∞ | бесконечность |
Математические символы в реальной жизни
Вы используете математические символы чаще, чем думаете, во всех сферах своей жизни.
Как отмечалось выше, разница между символом плюс или минус в банковском деле может указывать на то, добавляете ли вы большое количество средств на свой банковский счет или снимаете средства. Если вы когда-либо использовали электронную таблицу бухгалтерского учета, вы, вероятно, знаете, что знак большой суммы (∑) дает вам простой — действительно мгновенный — способ добавить бесконечный столбец чисел.
«Пи», обозначаемое греческой буквой π, используется во всем мире математики, науки, физики, архитектуры и других сфер. Несмотря на происхождение числа пи в предмете геометрии, это число находит применение во всей математике и даже проявляется в предметах статистики и вероятности.А символ бесконечности (∞) не только является важным математическим понятием, но также предполагает бесконечное пространство Вселенной (в астрономии) или бесконечные возможности, которые исходят от каждого действия или мысли (в философии).
Советы по символам
Хотя в этом списке указано больше математических символов, это одни из наиболее распространенных.
Вам часто потребуется использовать HTML-код, чтобы символы отображались в Интернете, поскольку многие шрифты не поддерживают использование математических символов.Однако вы также найдете большинство из них на графическом калькуляторе.
По мере вашего прогресса в математике вы начнете использовать эти символы все больше и больше. Если вы планируете изучать математику, это будет стоить вашего времени — и действительно сэкономит вам бесконечное (∞) количество этого ценного ресурса — если вы держите эту таблицу математических символов под рукой.
Правила знаков — математика дыхания
Число — это математический объект, используемый для измерения, маркировки и других математических операций. Основные математические операции — это сложение, вычитание, умножение и деление.
Дополнение:
сложение двух целых чисел — это общая сумма этих количеств.
Дополнение пишется со знаком плюс «+» между терминами; то есть в инфиксной записи.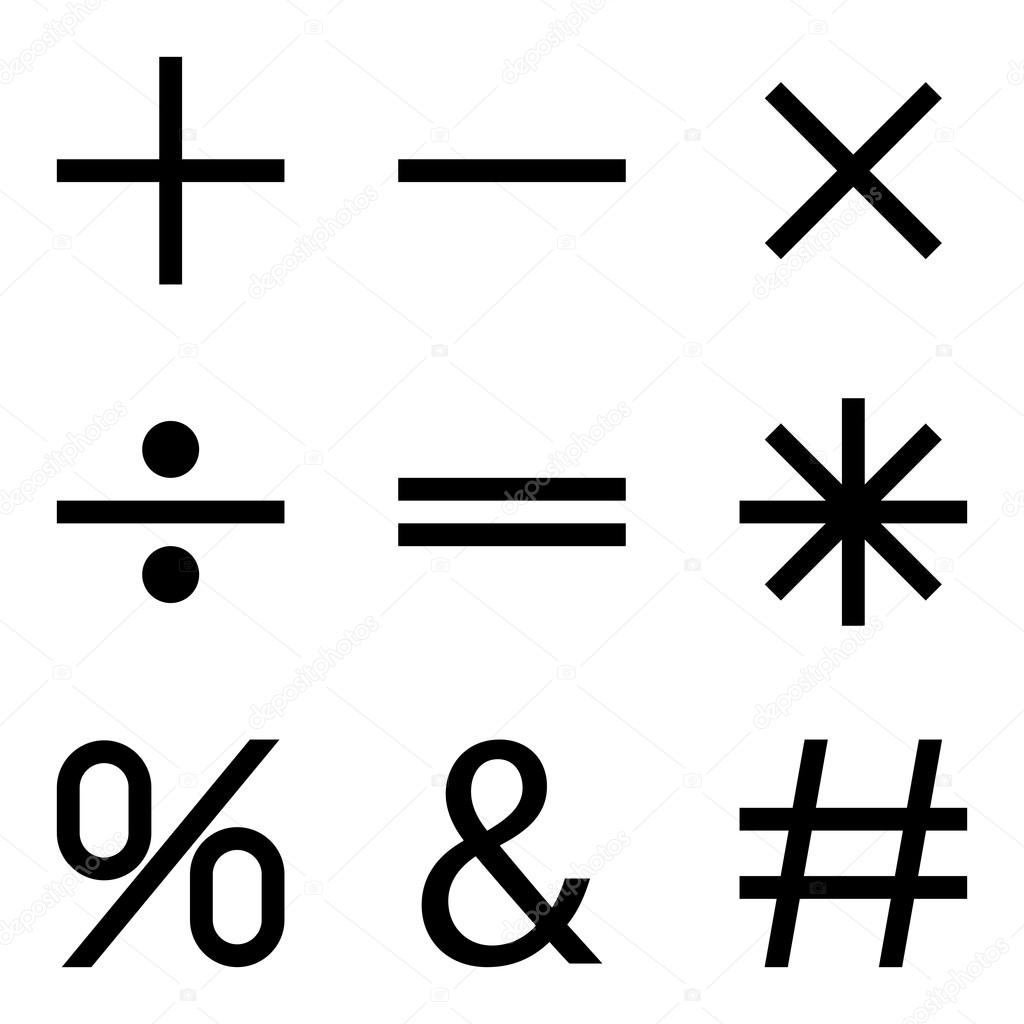
Результат обозначается знаком равенства. Например,
- («один плюс один равен двум»)
- («два плюс два равно четыре») и т. Д.
ПРАВИЛА ДОПОЛНИТЕЛЬНЫХ ЗНАКОВ:
Если знаки такие же, добавить знак и оставить прежним:
Случай 1: Если знак обоих чисел положительный, результат будет иметь положительный знак.
Например:
(а) (+3) + (+6) = (+9)
(б) (+18) + (+2) = (+20) и т. Д.,
Случай 2: Если знаки o оба числа отрицательны, результат будет иметь отрицательный знак.
Например:
(в) (-3) + (-6) = (-9)
(г) (-18) + (-2) = (-20) и т. Д.,
Если знаки разные, вычесть и оставить знак большего значения.
Случай 1: Если знак большего значения используется положительным знаком, то результат будет иметь положительный знак.
Например:
(д) (+6) + (-3) = (+3)
(ж) (-2) + (+18) = (+16)
Случай 2: Если для знака большего значения используется отрицательный знак, то результат будет иметь отрицательный знак.
Например:
(д) (-6) + (+3) = (-3)
(ж) (+2) + (-18) = (-16)
ВЫЧИСЛЕНИЕ:
Вычитание — это операция удаления объектов из коллекции. Он пишется со знаком «-» между терминами.Результат обозначается знаком равенства. Например,
- 2 — 1 = 1 («два минус один равно 1»)
- 5 — 3 = 2 («пять минус три равно два») и т. Д.
ПРАВИЛА ВЫЧИСЛЕНИЯ ЗНАКА:
Например,
Пр. 2: (-10) — (+8)
= (-10) + (-8) = (-18) [Изменил знак с (+8) на (-8), затем следовал правилу добавления знаков]
Пр. 3: (-10) — (-8)
= (-10) + (+8) = (-2) [Изменил знак с (-8) на (+8), затем следовал правилу добавления знаков]
Пр. 4: (+10) — (-8)
= (+10) + (+8) = (+18) [Знак изменен с (+8) на (-8), затем следовал правилу добавления знаков]
Пр. 5: (+10) — (+8)
= (+10) + (-8) = (+2) [Изменил знак с (+8) на (-8), затем следовал правилу добавления знаков]
Умножение:
Умножение можно рассматривать как повторное сложение; то есть умножение двух чисел эквивалентно сложению такого количества копий одного из них, множителя , и значения другого, множителя .
«Обычно множитель записывается первым, а множитель — вторым».
Умножение записывается со знаком «х» между членами. Результат обозначается знаком равенства. Например,
- 2 х 1 = 2
- 5 х 3 = 15.
Например, 4, умноженное на 3 (часто записывается как 3 x 4 и называется «3 умножить на 4»), можно вычислить, сложив 3 копии 4 вместе:
3 х 4 = 4 + 4 + 4 = 12
ПРАВИЛО ЗНАКА УМНОЖЕНИЯ:
ЕСЛИ ЗНАКИ ОДИНАКОВЫЕ, НЕСКОЛЬКО И ПОЛОЖИТЕ ПОЛОЖИТЕЛЬНЫЙ ЗНАК.
Случай 1: Если знаки положительные, умножьте и поставьте положительный знак.
Например:
(а) (+3) х (+6) = (+18)
(б) (+10) х (+2) = (+20)
Случай 2: Если знаки отрицательные, умножьте их и поставьте положительный знак.
Например:
(а) (-3) х (-6) = (+18)
(б) (-10) х (-2) = (+20)
ЕСЛИ ЗНАКИ ОТЛИЧАЮТСЯ, МНОЖЕСТВЕННО И ПОСТАВЛЯЙТЕ ОТРИЦАТЕЛЬНЫЙ ЗНАК, НЕ ОТВЕТИТЕЛЬНЫЙ ОТ ЗНАЧЕНИЯ НОМЕРА.
Например:
(а) (+3) х (-6) = (-18)
(б) (-3) х (+6) = (-18)
РАЗДЕЛ:
Деление противоположно умножению. Он пишется с использованием знака «÷ или /» между терминами. Результат обозначается знаком равенства.
Когда мы знаем факт умножения, мы можем найти деление факт:
ПРАВИЛО ЗНАКА ПОДРАЗДЕЛЕНИЯ:
ПРАВИЛО ЗНАКА РАЗДЕЛЕНИЯ ТАКОЕ, КАК УМНОЖЕНИЕ, ПОЭТОМУ СОБЛЮДАЙТЕ ПРАВИЛА ЗНАКА УМНОЖЕНИЯ.
Например:
(a) (-15) / 3 = (-5) [Правило знака умножения: если знаки разные, ставьте знак минус]
(b) (15) / (-3) = (-5) [Правило знака умножения: если знаки разные, поставить знак минус]
(c) (-15) / (-3) = (+5) [Правило знака умножения: если знаки одинаковые, то ставьте положительный знак]
(d) (+15) / (+3) = (+5) [Правило знака умножения: если знаки одинаковые, то поставить знак плюс]
Нравится:
Нравится Загрузка.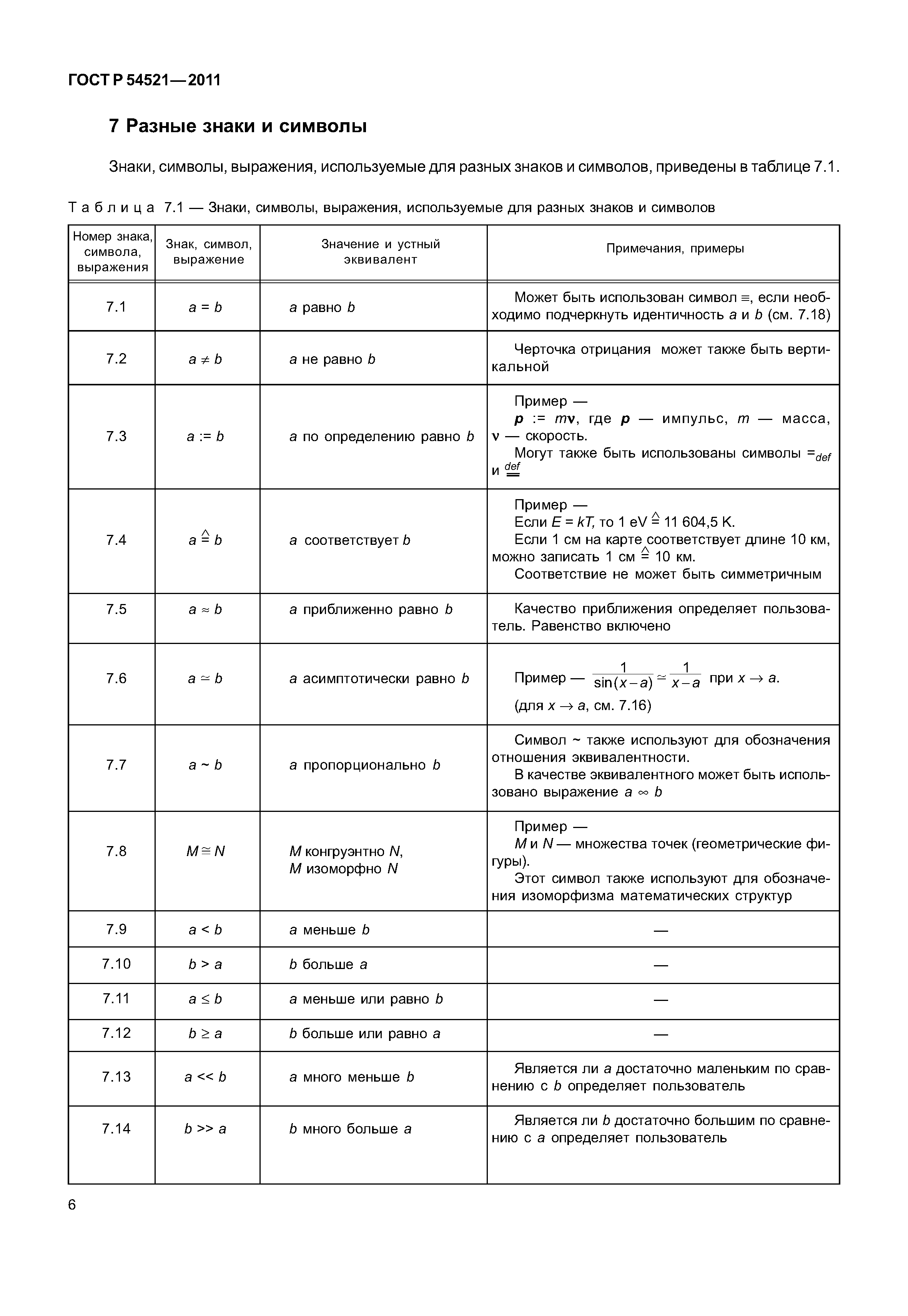
..
Некоторые математические символы
Умножение
Есть три широко используемых способа индикации умножения
- Символ « x », например, 5 x 6 = 30. Обратите внимание, что этого символа обычно избегают в алгебраических уравнениях из-за обычного использования «x» для обозначения неизвестной величины.
- Символ « * », например, 5 * 8 = 40. Использование звездочки для обозначения умножения обычно используется в электронных таблицах (например, в таблицах).g., Excel) и в алгебраических выражениях.
- Или просто число рядом с выражением в скобках, например, 5 (6 + 2) = 40
Дивизион
Есть три обычно используемых способа обозначения деления.
- «/», например, 40/5 = 8
- «÷», например, 30 ÷ 5 = 6
- Деление также можно указать, поместив одну величину (числитель) над другой величиной (знаменатель), как показано ниже.
44/123 = 0.3577
Равно (=) и не равно (≠)
2 + 3 = 5
2 + 3 ≠ 4
(Читается как «не равно» или «не равно».
Меньше (
<) и больше (>)- Символ <означает меньше . Например,
7 <8
200 <300
- Символ> означает больше . Например,
6> 4
3000> 2750
- Символ ≤ означает, что меньше или равно .
- Символ ≥ означает больше или равно .
Примерно равно
- Символ ≈ означает примерно равный .
Когда вам задают математическое выражение или уравнение, порядок выполнения математических операций очень важен. Правила для этого довольно простые. Рассмотрим следующий пример:
2 + (7 + 3) * 3 2 + 4 * (3-1) + 10
Сначала это может показаться устрашающим, но на самом деле это довольно просто.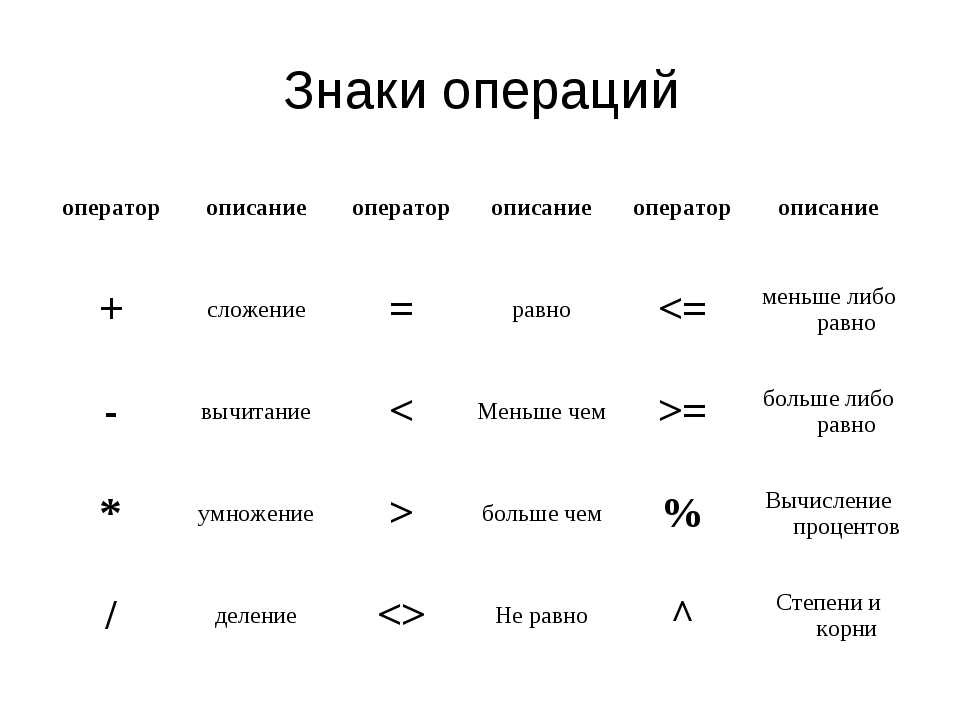
Правила приведены в таблице ниже.
Порядок действий
|
Итак, в приведенном выше примере вы бы:
- Решить в скобках
- Вычислить экспоненты
- Выполнить умножение и деление
- Выполнить сложение и вычитание
И правильный ответ — 110.
вернуться наверх | предыдущая страница | следующая страница
основных математических символов | Словарь
математика (BrE) | математика (AmE) — это краткая форма математики
На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.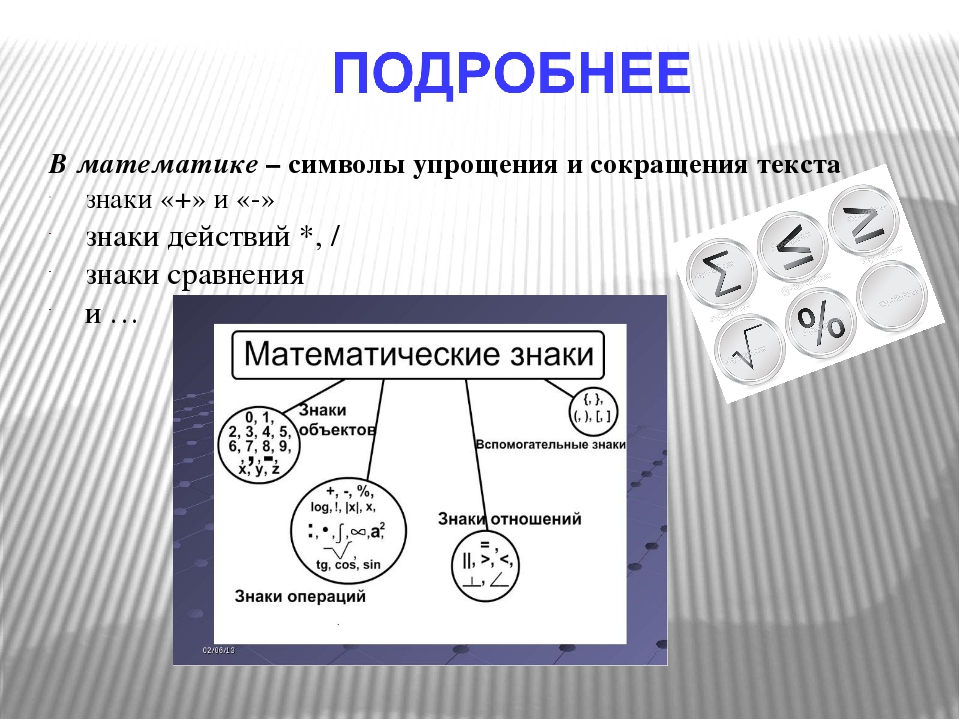
плюс / дополнительный знак
Знак плюс означает:
а.понятие
положительноеЛюбое число больше нуля является положительным числом и может быть написано со знаком плюс перед ним или без него.
Таким образом, +5 (плюс пять) и 5 (пять) — это одно и то же число.
г. операция сложения
3 + 5 = 8
три плюс пять равняется восьми
пять, добавленные к трем, составляют восемь
три, добавленные к пяти, составляют восемь
, если вы добавляете пять к трем, вы получаете восемь
Сложение дает нам сумму .В 3 + 5 = 8 получается восемь.
—
знак минус / знак вычитания
Знак минус означает:
а. понятие отрицательного
Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.
-3
минус три
г.
операция вычитания 8-5 = 3
восемь минус пять равняется трем
пять вычтено из восьми равняется трем
если вы вычтете пять из восьми, вы получите три
если вы вычтете пять из восьми, вы получите три
Вычитание дает нам разность .В 8-5 = 3 разница в три.
×
раз знак / знак умножения
Знак раз представляет:
умножение 5 x 6 = 30
пять умножить на шесть равно тридцать
пять умножить на шесть равно тридцать
пять шестерок равно тридцать
если умножить 5 на 6, получится тридцать
Умножение дает нам произведение . В 5 х 6 = 30 получается тридцать.
÷ ИЛИ /
делительный знак
Знак деления означает:
отдел
15 ÷ 3 = 5
15/3 = 5
пятнадцать делить на три равно пять
пять делятся на пятнадцать трижды
если пятнадцать разделить на три, получится пять
если три разделить на пятнадцать, получится пять
дает нам частное .
При 15 ÷ 3 = 5 частное равно пяти.
| рабочий | счет | ||
|---|---|---|---|
| дополнение | «плюс» | 2 + 2 = 4 | сумма |
| вычитание | «минус» | 5–3 = 2 | разница |
| умножение | «раз» | 3 х 5 = 15 | товар |
| отдел | «разделить на» | 21/7 = 3 | частное |
=
знак равенства
Знак равенства представляет равенство :
3 + 4 = 7
три плюс четыре равно семь
Обратите внимание, что мы обычно говорим, что равно НЕ равно:
- два плюс два равно четыре
-
два плюс два равны четыре
менее
3 <4
три меньше четырех
>
больше
4> 3
четыре больше трех
≠
НЕ равно
x ≠ z
x не равно z
≥
больше или равно
x ≥ z
x больше или равно z
≤
меньше или равно
z ≤ x
z меньше или равно x
¾
дробь
см.
Дроби
.
десятичный разделитель | точка
Десятичный разделитель отделяет целое число от дробной части справа:
1,23
В английском языке десятичным разделителем обычно является точка (.). Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,).
см. Десятичные числа
,
разделитель тысяч
В английском языке разделитель тысяч разделяет целые числа на группы по три справа.
10 987 654 321
В английском языке разделителем тысяч обычно является запятая (,).Обратите внимание, что в некоторых языках разделителем тысяч является точка (.) Или иногда пробел ().
см. Тыс.
%
знак процента
Знак процента указывает число или соотношение в виде доли от 100 ( процентов ).
40%
сорок процентов
За нее проголосовало всего сорок процентов людей.
Какой процент проголосовал за нее? Сорок процентов.
√
корень квадратный
√16 = 4
квадратный корень шестнадцати равен четырем
квадратный корень шестнадцати равен четырем
Запоминание знаков «больше, чем» и знаков «меньше»
Вы помните, как в школе изучали маленькие боковые указатели, похожие на маленькие наконечники стрел:
<>
Многие из нас знают, что эти знаки означают «больше» и «меньше», но, похоже, не могут вспомнить, какой знак какой.
Но сначала, что означают эти знаки?
Эти знаки используются, когда математические задачи не имеют однозначного ответа, что также называется неравенством. Неравенства сравнивают две вещи, показывая взаимосвязь между ними. Слово «неравенство» означает, что две вещи не равны.
Два знака <и> — это знаки, которые используются, когда вы сравниваете две вещи в математике. В математике вам обычно приходится решать проблему, но при использовании знаков больше или меньше вы показываете, больше или меньше число другого числа, а не решаете проблему.
Какой знак какой?
Символ> означает «больше». Он показывает, что одно число или значение больше другого числа. Например: 5> 2
Если вы видите символ <, это означает, что одно число меньше другого. Для экзамена: 2 <6
Символы выглядят одинаково, и их легко спутать, выбрав какой символ.
Открытые концы
Самый простой способ запомнить, какой символ — это запомнить, что открытый конец символа всегда обращен к большему числу, а стрелка указывает на маленькое число.
Метод аллигатора
Еще один способ запомнить знаки больше и меньше — это то, что вы, возможно, помните из начальной школы: метод аллигатора.
Представьте себе символы в виде пасти аллигатора с числами на каждой стороне, изображающими рыбки. Аллигатор всегда захочет съесть большее количество рыбы. Какое бы число ни было больше, пасть аллигатора открывается навстречу этому числу.