Таблица знаков в геометрии и их значения: пересечение, подобие
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
| Знак | Название | Значение/описание | |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | |
| ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />»> | острый угол | угол от 0 до 90 градусов | ∠AOB = 60° |
| прямой угол | угол, равный 90 граусам | ∠AOB = 90° | |
| угол от 90 до 180 градусов | ∠AOB = 120° | ||
| ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />»> | развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) | единица измерения угла, равна 1/360 окружности | 45° | |
| ′ | единица измерения угла, 1° = 60′ | α = 70°59′ | |
| ″ | единица измерения угла, 1′ = 60″ | α = 70°59′59″ | |
| ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />»> | линия | бесконечная прямая без начала и конца | |
| ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />»> | отрезок | участок на прямой между точками A и B | |
| ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />»> | луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | |
| ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />»> | дуга | дуга, образованная между точками A и B | |
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность | элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | 141592654…</nobr>» data-order=»<nobr>π = 3.141592654…</nobr>»>π = 3.141592654… |
| рад (rad) или c | радиан | единица измерения угла | 360° = 2π c |
microexcel. ru
ru
Знаки больше, меньше или ровно в математике
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
- Строгие неравенства — используют только знак больше (>) или меньше (<).

- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- неравенства a > b и b < a означают одно и тоже, то есть равносильны.
- Нестрогие неравенства — используют знаки сравнения ≥ (больше или равно) или ≤ (меньше или равно).
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
- Другие типы неравенств.
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Геометрия знак и символ
«Эта наука является воротами, через которые мы движемся к знанию сущности души,
потому что это – корень всего знания» (из текста «Братства чистоты»). За
символизмом геометрических форм стоит восприятие разнообразных форм природы как
облачений единого Бога и как проявление множественности, отражающей единство.
Через геометрические формы и их ритм раскрывается метафизическая значимость мира
и происходит распознавание небесных архетипов в космосе и в уме.
За
символизмом геометрических форм стоит восприятие разнообразных форм природы как
облачений единого Бога и как проявление множественности, отражающей единство.
Через геометрические формы и их ритм раскрывается метафизическая значимость мира
и происходит распознавание небесных архетипов в космосе и в уме.
Символ Инь и Ян
Точка, линия, круг
Крест кельтов
Определенные геометрические формы обладают силой глубокого проникновения в душу. Посетители Парфенона испытывают чувство глубочайшего успокоения, которое длится несколько дней. Напряженное величие готических соборов будит чувство безграничности и духовного дерзновения. Формы несут в себе чувство симметрии или асимметрии, баланса или неустойчивости, тревоги или успокоения.
Точка, линия и круг – это основные элементы геометрических форм.
Форма креста – одного из наиболее древних и распространенных символов – несет в себе чувство баланса и
уравновешенности земного и небесного принципов. Во многих культурах крест
представляет космос: вертикальная линия означает духовный мужской принцип,
горизонтальная – женский, земной. Точка их пересечения означает встречу неба и
земли, химическую свадьбу розенкрейцеров, и в результате этой встречи возникает
идея креста как человеческой судьбы.
Во многих культурах крест
представляет космос: вертикальная линия означает духовный мужской принцип,
горизонтальная – женский, земной. Точка их пересечения означает встречу неба и
земли, химическую свадьбу розенкрейцеров, и в результате этой встречи возникает
идея креста как человеческой судьбы.
Круг – это архетипическая форма всех геометрических форм, содержащихся внутри него. Круг означает идею совершенства, бесконечности и вечности. Используется как нимб для обозначения святости. Как монограмма Бога представляет собой не только совершенство, но и Его бесконечность: «Тот, кто был в начале и теперь, и кому не будет конца». Это – знак мужского духовного принципа. Является символом бога.
Квадрат по контрасту с кругом представляет плотность: статическое совершенство,
земной и материальный аспект бытия. Он означает устойчивость, безопасность, надежность. Используется
как нимб для обозначения святости живых. В индийской символике означает порядок
во Вселенной и равновесие противоположностей. Знак кватернера.
Знак кватернера.
Равнобедренный треугольник представляет цифру три, священную Троицу, стяжание трех принципов в один. Вершина треугольника, направленная вверх, означает устремленность энергии к небу. Это знак огня и активного мужского принципа. Треугольный нимб используется для представления Бога Отца или Троицы. Монограмму Троицы в западном христианстве выражает треугольник с тремя кольцами, означающими три ипостаси одного Бога: Бога Отца, Сына и Духа Святого. Треугольник, повернутый вершиной вниз, означает нисхождение энергии с неба. Это – знак воды и пассивного женского элемента.
Комбинация круга, треугольника и квадрата или прямоугольника,
помещенных один под другим, используется соответственно для обозначения мира
Божественного, человеческого и подземного. Верхний круг означает первопричину
творения с лучами творения, расходящимися во все стороны: изливающимся вверх и
вниз. Второй круг используется для обозначения мира ангелов и высшей духовной
иерархии, находящейся под Богом. Треугольник, вторгающийся в круг и обращенный
вершиной вверх, состоит из четырех треугольников. Его верхняя часть означает
небо со звездами, ангелами и изображенным здесь знаком планеты Меркурий как
гением астрологии. Земля представлена серой, камнями и зверями. Воздух –
метеорами, планетами и рыбами. Вода – металлами, рыбой и солью. Человечество
помещено в круге между небом и землей. Эта сложная композиция XVII века помещена
на прямоугольник, означающий объятый огнем ад, в центре которого помещен в
полукруге – знак незавершенности – Сатана.
Треугольник, вторгающийся в круг и обращенный
вершиной вверх, состоит из четырех треугольников. Его верхняя часть означает
небо со звездами, ангелами и изображенным здесь знаком планеты Меркурий как
гением астрологии. Земля представлена серой, камнями и зверями. Воздух –
метеорами, планетами и рыбами. Вода – металлами, рыбой и солью. Человечество
помещено в круге между небом и землей. Эта сложная композиция XVII века помещена
на прямоугольник, означающий объятый огнем ад, в центре которого помещен в
полукруге – знак незавершенности – Сатана.
В буддийском контексте круг означает постоянный цикл изменений. Графически это выражается в колесе жизни. Над ним
изображаются небесные реалии, сменяющиеся по движению часовой стрелки картинами
завистливых богов – титанов, привязанных к земле привидений – голодных духов,
потом миром зверей и человечеством. Колесо держит бог смерти Яма как воплощение
трех иллюзий, привязывающих человека к колесу жизни: сладострастие, воплощенное
фигурой красного петуха, зеленой змеей ненависти и черной свиньей невежества. Пентаграмма бесконечна как круг. Означает совершенство и полноту. Состоит из
треугольных компонентов, означающих четыре элемента и пятый – это духовный
принцип. Эти двойственные характеристики дают этому символу возможность
притягивать или отгонять злых духов и потому этот пятиугольник используется
магами. Впервые использовался последователями Пифагора. Известен также как
пентакль дьявола и как советский пентакль.
Пентаграмма бесконечна как круг. Означает совершенство и полноту. Состоит из
треугольных компонентов, означающих четыре элемента и пятый – это духовный
принцип. Эти двойственные характеристики дают этому символу возможность
притягивать или отгонять злых духов и потому этот пятиугольник используется
магами. Впервые использовался последователями Пифагора. Известен также как
пентакль дьявола и как советский пентакль.
Что означает знак дуга в геометрии
САТ Агни Партнеры Погружение в Новостной раздел. Страница, которую Вы пытаетесь открыть не найдена или была удалена.
Не круг, так дуга», не шунь, так ни», не само крутится, так все крутится» (слова Шэнь Цзячжэня). Что означает требование внутренняя поверхность бедер движется по нижней дуге»?
Знаки и символы часть 2 — Город Творцов
Геометрические символы стабильны и передаются из поколения в. Арка (дуга), в первую очередь, – символ небесного свода, бога Неба. В обрядах инициации прохождение через арку означает новое рождение после полного
В обрядах инициации прохождение через арку означает новое рождение после полного
Журнальный зал Апология математики, или О математике
Кстати, и имя Пан родственно имени Вишну, означая «все». Следовательно, Прото-Вишну тождественен Прото-Пану. Космический знак (как и всякий знак вообще) — всегда некоторое вторичное явление, указывающее на некоторую скрытую
—Паулус Александринус Венера, Лот Любви Дневной Лот = Asc. + Ve — PS Ночной Лот = Asc. + PS — Ve «Любовь означает неосознанную потребность и неконтролируемые желания.
Символ представляющий собой дугу «активности» и незавершенный знак бесконечности со стрелой на конце, характеризуется как система направляющая всю свою энергию на процессы изменения внутреннего содержания, то есть на совершенство. Крайние дуги, стремящиеся к сохранению и накоплению энергетического потенциала, сравнительно
По готовым рисункам определить радиусы, хорды, диаметры, дуги. Геометрия» означает землемерие». Презентация: Введение в геометрию, Урок: Геометрия, Класс: 7. Что изучает геометрия.
Презентация: Введение в геометрию, Урок: Геометрия, Класс: 7. Что изучает геометрия.
Тема: Геометрия Лобачевского» Выполнила: Зайнулина Г. Г.Бишкек 2010 Н.И. Лобачевский и его геометрия До начала XIX столетия ни одна из попыток доказательства V постулата не увенчалась успехом. Таким образом, проблема V постулата оставалась Пусть меньше полуокружности, и, значит, d(A,B) — длина этой дуги.
| |
Рассылка выходит раз в сутки и содержит список программ из App Store для iPhone перешедших в категорию бесплатные за последние 24 часа.
Математический знаки и символы
«Символы не являются только записью мыслей,
средством её изображения и закрепления, –
нет, они воздействуют на самую мысль,
они… направляют её, и бывает достаточно
переместить их на бумаге… для того, чтобы
безошибочно достигнуть новых истин».
Л.Карно
Математические знаки служат в первую очередь для точной (однозначно определённой) записи математических понятий и предложений. Их совокупность в реальных условиях их применения математиками составляет то, что называется, математическим языком.
Математические знаки позволяют записывать в компактной форме предложения, громоздко выраженные на обычном языке. Это облегчает их запоминание.
Прежде чем использовать в рассуждениях те или иные знаки, математик старается сказать, что каждый из них обозначает. Иначе его могут не понять.
Но математики не всегда могут сказать сразу, что отражает тот или иной символ, введённый ими для какой-либо математической теории. Например, сотни лет математики оперировали отрицательными и комплексными числами, однако объективный смысл этих чисел и действие с ними удалось раскрыть лишь в конце XVIII и в начале XIX века.
1. Символизм математических кванторов
Подобно обычному языку, язык математических знаков позволяет обмениваться установленными математическими истинами, но являясь лишь вспомогательным средством, присоединяемым к обычному языку и без него существовать, не может.
Математическое определение:
На обычном языке:
Пределом функции F (x) в некоторой точке X0 называется постоянное число А, такое что для произвольного числа Е>0 существует такое положительное d(E), что из условия |X – X0|<d вытекает неравенство |F(x)–A|<E
Запись в кванторах (на математическом языке)
|
2. Символизм математических знаков и геометрических фигур.
1) Бесконечность — концепция, используемая в математике, философии и естественных науках. Бесконечность какого-то понятия или атрибута некоторого объекта означает невозможность указать для него границы или количественную меру. Термин бесконечность соответствует нескольким различным понятиям, в зависимости от области применения, будь то математика, физика, философия, теология или повседневная жизнь. В математике не существует одного понятия бесконечности, она наделяется особыми свойствами в каждом разделе. Более того, эти различные «бесконечности» не взаимозаменяемы. К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Скажем, количество целых чисел бесконечно большое (оно называется счётным). Чтобы обобщить понятие количества элементов для бесконечных множеств, в математике вводится понятие мощности множества. При этом не существует одной «бесконечной» мощности. Например, мощность множества действительных чисел больше мощности целых чисел, потому что между этими множествами нельзя построить взаимно-однозначное соответствие, а целые числа включены в действительные. Таким образом, в этом случае одно кардинальное число (равно мощности множества) «бесконечнее» другого. Основоположником этих понятий был немецкий математик Георг Кантор. В математическом анализе ко множеству действительных чисел добавляются два символа, плюс и минус бесконечность, применяющиеся для определения граничных значений и сходимости. Нужно отметить, что в этом случае речь об «осязаемой» бесконечности не идёт, так как любое утверждение, содержащее этот символ, можно записать, используя только конечные числа и кванторы.
К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Скажем, количество целых чисел бесконечно большое (оно называется счётным). Чтобы обобщить понятие количества элементов для бесконечных множеств, в математике вводится понятие мощности множества. При этом не существует одной «бесконечной» мощности. Например, мощность множества действительных чисел больше мощности целых чисел, потому что между этими множествами нельзя построить взаимно-однозначное соответствие, а целые числа включены в действительные. Таким образом, в этом случае одно кардинальное число (равно мощности множества) «бесконечнее» другого. Основоположником этих понятий был немецкий математик Георг Кантор. В математическом анализе ко множеству действительных чисел добавляются два символа, плюс и минус бесконечность, применяющиеся для определения граничных значений и сходимости. Нужно отметить, что в этом случае речь об «осязаемой» бесконечности не идёт, так как любое утверждение, содержащее этот символ, можно записать, используя только конечные числа и кванторы. Эти символы (как и многие другие) были введены для сокращения записи более длинных выражений. Бесконечность также неразрывно связана с обозначением бесконечно малого, к примеру, ещё Аристотель сказал:
Эти символы (как и многие другие) были введены для сокращения записи более длинных выражений. Бесконечность также неразрывно связана с обозначением бесконечно малого, к примеру, ещё Аристотель сказал:
«… всегда возможно придумать большее число, потому что количество частей, на которые можно разделить отрезок, не имеет предела; поэтому бесконечность потенциальна, никогда не действительна, и какое бы число делений не задали, всегда потенциально можно поделить этот отрезок на еще большее число». Заметим, что Аристотель внес большой вклад в осознание бесконечности, разделив её на потенциальную и актуальную, и вплотную подошел с этой стороны к основам математического анализа, также указав на пять источников представления о ней:
- время,
- разделение величин,
- неиссякаемость творящей природы,
- само понятие границы, толкающее за её пределы,
- мышление, которое неостановимо.
Бесконечность в большинстве культур появилась как абстрактное количественное обозначение чего-то непостижимо большого, в применении к сущностям без пространственных или временных границ.
Далее бесконечность получила развитие в философии и теологии наравне с точными науками. К примеру, в теологии бесконечность Бога не столько даёт количественное определение, сколько означает неограниченность и непостижимость. В философии это атрибут пространства и времени.
Современная физика вплотную подходит к отрицаемой Аристотелем актуальности бесконечности — то есть доступности в реальном мире, а не только в абстрактном. Например, есть понятие сингулярности, тесно связанное с чёрными дырами и теорией большого взрыва: это точка в пространстве—времени, в которой масса в бесконечно малом объёме сосредоточена с бесконечной плотностью. Уже есть солидные косвенные доказательства существования чёрных дыр, хотя теория большого взрыва находится ещё в стадии разработки.
2) Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку. Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Если радиус равен нулю, то круг вырождается в точку. Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Круг – символ Солнца, Луны. Один из самых распространённых символов. А также является символом бесконечности, вечности, совершенства.
3) Квадрат (ромб) – является символом комбинации и упорядочивания четырёх различных элементов, например четыре основных стихий или четырёх времён года. Символ числа 4, равенства, простоты, прямоты, истины, справедливости, мудрости, чести. Симметрия является той идеей посредством которой человек пытается постичь гармонию и с давних времён считалась символом прекрасного. Симметрией обладают так называемые “фигурные” стихи, текст которых имеет очертание ромба.
Стихотворение – ромб.
Мы –
Среди тьмы.
Глаз отдыхает.
Сумрак ночи живой.
Сердце жадно вздыхает,
Шепот звёзд долетает порой.
И лазурные чувства теснятся толпой.
Всё забылось в блеске росистом.
Поцелуем душистым!
Поскорее блесни!
Снова шепни,
Как тогда:
«Да!»(Э.Мартов, 1894г)
4) Прямоугольник. Из всех геометрических форм это наиболее рациональная, наиболее надёжная и правильная фигура; эмпирически это объясняется тем фактом, что всегда и везде прямоугольник был излюбленной формой. С помощью него человек приспосабливал пространство или какой-либо предмет для непосредственного использования в своём быту, например: дом, комната, стол, кровать и т.п.
5) Пентагон – правильный пятиугольник в виде звезды символ вечности, совершенства, вселенной. Пентагон – амулет здоровья, знак на дверях для того, чтобы отогнать ведьм, эмблема Тота, Меркурия, кельтского Гавайна и др., символ пяти ран Иисуса Христа, благополучия, удачи у евреев, легендарный ключ Соломона; знак высокого положения в обществе у Японцев.![]()
6) Правильный шестиугольник, гексагон – символ изобилия, красоты, гармонии, свободы, брака, символ числа 6, образ человека (две руки, две ноги, голова и туловище).
7) Крест – символ высших сакральных ценностей. Крест моделирует духовный аспект, восхождение духа, устремление к богу, к вечности. Крест – универсальный символ единства жизни и смерти.
Конечно, с этими утверждениями можно и не соглашаться.
Однако никто не будет отрицать, что любое изображение вызывает у человека ассоциации. Но проблема в том, что одни предметы, сюжеты или графические элементы вызывают у всех людей (вернее, у многих) одинаковые ассоциации, а другие – совершенно различные.
8) Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Свойства треугольника как фигуры: прочность, неизменяемость.
Аксиома А1 стереометрии гласит: «Через 3 точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна!»
Чтобы проверить глубину понимания этого утверждения обычно задают задачу на засыпку: «На столе сидят три мухи, на трёх концах стола. В определённый момент они разлетаются по трём взаимно – перпендикулярным направлениям с одинаковой скоростью. Когда они снова окажутся в одной плоскости?». Ответом служит тот факт, что три точки всегда, в любой момент, определяют единственную плоскость. И именно 3 точки определяют треугольник, поэтому эта фигура в геометрии считается самой устойчивой и прочной.
В определённый момент они разлетаются по трём взаимно – перпендикулярным направлениям с одинаковой скоростью. Когда они снова окажутся в одной плоскости?». Ответом служит тот факт, что три точки всегда, в любой момент, определяют единственную плоскость. И именно 3 точки определяют треугольник, поэтому эта фигура в геометрии считается самой устойчивой и прочной.
Треугольник обычно относят к острой, «наступательной» фигуре, связанной с мужским началом. Равносторонний треугольник – мужской и солнечный знак, представляющий божество, огонь, жизнь, сердце, гору и восхождение, благополучие, гармонию и королевскую власть. Перевёрнутый треугольник – женский и лунный символ, олицетворяет воду, плодовитость, дождь, божественную милость.
9) Шестиконечная Звезда (Звезда Давида) – состоит из двух наложенных один на другой равносторонних треугольников. Одна из версий происхождения знака связывает его форму с формой цветка Белой лилии, имеющего шесть лепестков. Цветок традиционно располагался под храмовым светильником, таким образом, что священник зажигал огонь, как бы, в центре Маген Давида.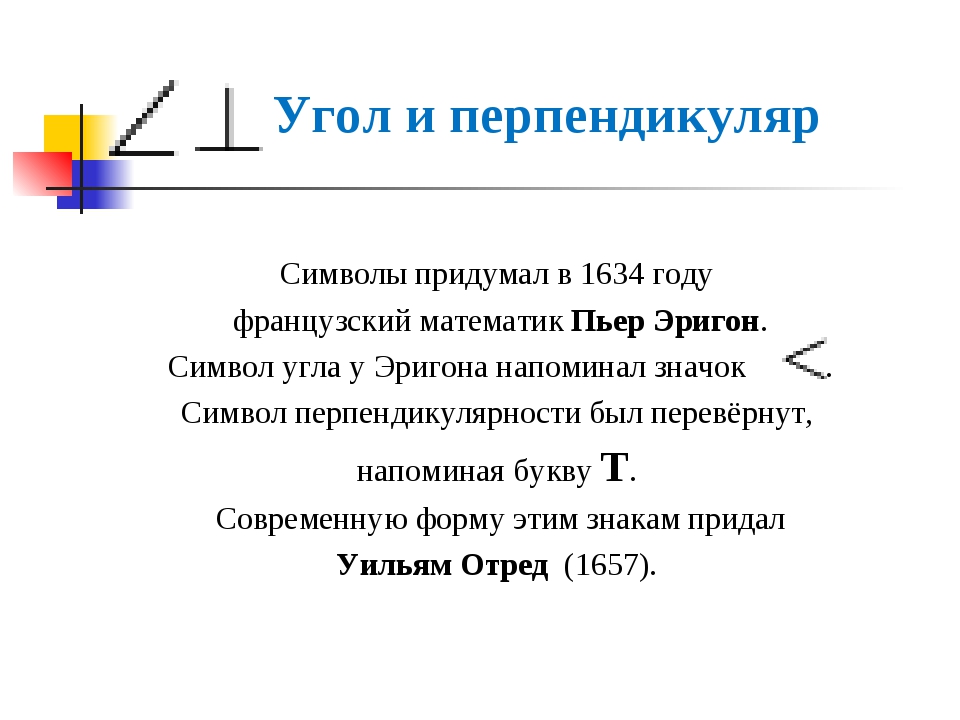 В каббале два треугольника символизируют свойственную человеку дуальность: добро против зла, духовное против физического и так далее. Треугольник, направленный остриём вверх, символизирует наши добрые дела, которые поднимаются на небеса и вызывают поток благодати, нисходящий обратно в этот мир (что символизирует треугольник, направленный вниз). Иногда Звезду Давида называют Звездой Творца и связывают каждый из её шести концов с одним из дней недели, а центр – с субботой.
В каббале два треугольника символизируют свойственную человеку дуальность: добро против зла, духовное против физического и так далее. Треугольник, направленный остриём вверх, символизирует наши добрые дела, которые поднимаются на небеса и вызывают поток благодати, нисходящий обратно в этот мир (что символизирует треугольник, направленный вниз). Иногда Звезду Давида называют Звездой Творца и связывают каждый из её шести концов с одним из дней недели, а центр – с субботой.
Государственные символы США также содержат Шестиконечную Звезду в разных видах, в частности есть она на Большой печати США и на денежных знаках. Звезда Давида изображена на гербах немецких городов Шер и Гербштедт, а так же украинских Тернополя и Конотопа. Три шестиконечные звезды изображены на флаге Бурунди и олицетворяют национальный девиз: «Единство. Работа. Прогресс».
В христианстве шестиконечная звезда – символ Христа, а именно соединения во Христе божественной и человеческой природы. Именно поэтому этот знак вписан в Православный Крест.
10) Пятиконечная Звезда – Основной отличительной эмблемой большевиков является красная пятиконечная звезда, официально установленная весной 1918 года. Первоначально большевистская пропаганда назвала её “ Марсовой звездой” ( якобы принадлежащей античному богу войны – марсу), а затем стала заявлять, что “ Пять лучей звезды, означает союз трудящихся всех пяти континентов в борьбе против капитализма”. В действительности же пятиконечная звезда не имеет никакого отношения ни к воинствующему божеству Марсу, ни к международному пролетариату, это – древний оккультный знак (очевидно ближневосточного происхождения), называющийся “пентаграммой” или “Звездой Соломона”.
Правительству”, находящемуся под полным контролем масонства.
Весьма часто сатанисты рисуют пентаграмму двумя концами вверх, чтобы туда было легко вписать дьявольскую голову “Пентаграмма Бафомета”. Портрет “Пламенного революционера” помещён внутри “Пентаграммы Бафомета”, являющейся центральной частью композиции проектируемого в 1932 году особого чекистского ордена “ Феликса Дзержинского” (далее проект был отклонён Сталиным, глубоко ненавидящим “Железного Феликса”).
Отметим, что зачастую пентаграмма размещалась большевиками на красноармейском обмундировании, в военной технике, различных знаках и всевозможных атрибутах наглядной агитации чисто по-сатанински: двумя “рогами” вверх.
Марксистские планы “всемирной пролетарской революции” имели явно масонское происхождение, ряд виднейших марксистов состоял в масонстве. К ним относился Л.Троцкий, именно он и предложил сделать масонскую пентаграмму опознавательной эмблемой большевизма.
Интернациональные масонские ложи тайно оказывали большевикам всестороннюю поддержку, особенно финансовую.
3. Масонские знаки
Масоны
Девиз: «Свобода. Равенство. Братство».
Общественное движение свободных людей, которые на основе свободного выбора позволяют стать лучше, стать ближе к богу следственно, они признаны улучшить мир.
Масоны – соратники Творца, сподвижники общественного прогресса, против инерции, косности и невежества. Выдающиеся представители масонства – Карамзин Николай Михайлович, Суворов Александр Васильевич, Кутузов Михаил Илларионович, Пушкин Александр Сергеевич, Геббельс Иозеф.
Выдающиеся представители масонства – Карамзин Николай Михайлович, Суворов Александр Васильевич, Кутузов Михаил Илларионович, Пушкин Александр Сергеевич, Геббельс Иозеф.
Знаки
Лучезарное око (дельта) – знак древний, религиозный. Он говорит о том, что Бог надзирает над творениями своими. Изображением этого знака масоны спрашивали у Бога благословения на какие-либо грандиозные действия, на труды свои. Лучезарное око расположено на фронтоне Казанского Собора в Санкт-Петербурге.
Сочетание циркуля и угольника в масонском знаке.
Для непосвящённого – это орудие труда (каменщика), а для посвящённых – это способы познания мира и соотношения божественной премудрости и человеческого разума.
Угольник, как правило, снизу – это человеческое познание мира. С точки зрения масонства, человек приходит в мир, что познать божественный замысел. А для познания необходим инструментарий. Самая эффективная наука в познание мира – математика.
Угольник – древнейший математический инструмент, известный с незапамятных времён. Градуировка угольника – уже большой шаг вперёд в математическом инструментарии познания. Человек познаёт мир с помощью наук математика из них первейшая, но не единственная.
Однако угольник деревянный, и он вмещает то, что может вместить. Его нельзя раздвинуть. Если ты попытаешься его раздвинуть, чтобы он вмещал больше, – ты поломаешь его.
Так люди, пытающиеся познать всю бесконечность божественного замысла, либо умирают, либо сходят с ума. «Знай, свои границы!» – вот, что сообщает Миру этот знак. Будь ты даже Эйнштейн, Ньютон, Сахаров – величайшие умы человечества! – понимай, что ты ограничен временем, в котором ты рождён; в познании мира, языком, объёмом мозга, самыми разными человеческими ограничениями, жизнью твоего тела. Поэтому – да, познавай, но понимай, что ты никогда до конца не познаешь!
А циркуль? Циркуль есть божественная премудрость. Циркулем можно описать круг, а если раздвинуть ему ножки, то будет прямая. А в символических системах круг и прямая – две противоположности. Прямая обозначает человека, его начало и конец (как тире между двумя датами – рождения и смерти). Круг – символ божества, поскольку является совершенной фигурой. Они друг другу противостоят – божественная и человеческая фигуры. Человек не совершенен. Бог – совершенен во всём.
А в символических системах круг и прямая – две противоположности. Прямая обозначает человека, его начало и конец (как тире между двумя датами – рождения и смерти). Круг – символ божества, поскольку является совершенной фигурой. Они друг другу противостоят – божественная и человеческая фигуры. Человек не совершенен. Бог – совершенен во всём.
Для божественной премудрости нет невозможного, она может принять и вид человеческий (–) и вид божественный (0), всё может в себя вместить. Таким образом, человеческий разум постигает божественную премудрость, объемлет ее. В философии это утверждение является постулатом об абсолютной и относительной истине.
Люди всегда познают истину, но всегда относительную истину. А абсолютная истина ведома только Богу.
Познавай всё больше, осознавая, что не сможешь познать истину до конца – какие глубины мы находим в обыкновенном циркуле с угольником! Кто бы мог подумать!
Вот в чём прелесть и очарование масонской символики, в её огромной интеллектуальной глубине.
Начиная с эпохи Средневековья циркуль, как инструмент для вычерчивания безупречных кругов стал символом геометрии, космического порядка и планомерных действий. В это время часто рисовали Бога Саваофа в образе творца и архитектора Вселенной с циркулем в руках (Уильям Блейк ‘‘Великий Архитектор’’, 1794 г).
Шестиугольная Звезда (Вифлеема)
Буква G – обозначение бога (нем. – Got), великого геометра Вселенной.
Шестиугольная Звезда, означала Единство и Борьбу Противоположностей, борьбу Мужчины и Женщины, Добра и Зла, Света и Тьмы. Не может одно существовать без другого. Напряжение, которое возникает между этими противоположностями, создаёт мир в том виде, в каком мы его знаем.
Треугольник вверх означает – «Человек стремится к Богу». Треугольник вниз – «Божество нисходит к Человеку». В их соединении и существует наш мир, который и есть соединение Человеческого и Божественного. Буква G здесь означает, что Бог живёт в нашем мире. Он реально присутствует во всём, им сотворённом.
Заключение
Математические знаки служат в первую очередь для точной записи математических понятий и предложений. Их совокупность составляет то, что называется математическим языком.
Решающей силой развития математической символики является не “свободная воля” математиков, а требования практики, математических исследований. Именно реальные математические исследования помогают выяснить, какая система знаков наилучшим образом отображает структуру количественных и качественных отношений, в силу чего могут быть эффективным орудием их дальнейшего применения в символах и эмблемах.
Что означает знак бесконечности? Происхождение и значение
Знак бесконечности
Прежде всего, давайте определим, значение этого знака. Этот знак, находит применение в таких науках как математика, геометрия, физика, философия, логика и в других. Характеризуется не исчисляемыми, беспредельными, величинами, предметами и явлениями, для которых невозможно выяснить ни количество меры, ни рамок границы.
Это знак в том виде, в котором мы его знаем, был начертан математиком Джоном Валлисом в 1655 году. Есть много предположений, о том, что именно вдохновило англичанина на выбор именно такого изображения бесконечности. Существует мнение, это была буква греческого алфавита омега. Также есть вероятность того что он имеет римское происхождение от числа 1000, в 16 веке оно выглядело как «CIƆ», и имело значение – «много».
Символу бесконечности часто придают мистическое значение. Все мы знаем арабское число «8», именно это число является мистическим в культуре многих народов. Для евреев восьмерка число Господа. Для греческого математика и мистика Пифагора восьмерка несла значение гармонии и стабильности. В Китае – символ удачи и т.д.
Считается, что восьмерка, если положить её на бок становится аналогом знака бесконечности. Но это не делает её бесконечностью как таковой. Не стоит путать древнее происхождение восьмерки со сравнительно недавно появившимся символом обозначающем бесконечность.![]()
Часто бесконечности, приписывают свойства одного из древнейших символов Уробороса. Они в чем-то схожи, но в отличие от Уробороса бесконечность гораздо более узкая и ограниченная по своей сути. Рассмотрим детальней. Понятие Уробороса включает постоянный цикличный переход одного в другое. Например, дня в ночь, создания и разрушения, бесконечного цикла действий не имеющих завершения. Уроборос изображается как змей, кусающий себя за хвост. Аналоги этого символа встречаются в мифологии практически всех народностей.
В заключении хотелось бы подчеркнуть, что символ бесконечности абсолютно самостоятельный, знак, а явление бесконечности активно исследуется математиками и философами нашего времени.
Что означает?
1. Знак пятиконечной звезды?
Значение имени Геометрия: происхождение, судьба, характер, национальность, перевод, написание
Что означает имя Геометрия? Что обозначает имя Геометрия? Что значит имя Геометрия для человека? Какое значение имени Геометрия, происхождение, судьба и характер носителя? Какой национальности имя Геометрия? Как переводится имя Геометрия? Как правильно пишется имя Геометрия? Совместимость c именем Геометрия — подходящий цвет, камни обереги, планета покровитель и знак зодиака. Полная характеристика имени Геометрия и его подробный анализ вы можете прочитать онлайн в этой статье совершенно бесплатно.
Полная характеристика имени Геометрия и его подробный анализ вы можете прочитать онлайн в этой статье совершенно бесплатно.
Содержание толкования имени
Анализ имени Геометрия
Имя Геометрия состоит из 9 букв. Имена из девяти букв – признак склонности к «экономии энергии» или, проще говоря – к лени. Таким людям больше всего подходит образ жизни кошки или кота. Чтобы «ни забот, ни хлопот», только возможность нежить свое тело, когда и сколько хочется, а так же наличие полной уверенности в том, что для удовлетворения насущных потребностей не придется делать «лишних движений». Проанализировав значение каждой буквы в имени Геометрия можно понять его тайный смысл и скрытое значение.
 Выступают в роли посредника в конфликтах. Проницательны, понимают мир тайн. Болтливы. Сильная любовь к путешествиям, в жизни такие могут часто менять место жительства, непоседливы.
Выступают в роли посредника в конфликтах. Проницательны, понимают мир тайн. Болтливы. Сильная любовь к путешествиям, в жизни такие могут часто менять место жительства, непоседливы. Часто желания не совпадают с возможностями. Стремятся сделать все быстро, не откладывая на завтра. Требовательность к окружающим и к себе. Стремление к поиску истины. Переоценка своих возможностей.
Часто желания не совпадают с возможностями. Стремятся сделать все быстро, не откладывая на завтра. Требовательность к окружающим и к себе. Стремление к поиску истины. Переоценка своих возможностей.Значение имени Геометрия в нумерологии
Нумерология имени Геометрия может подсказать не только главные качества и характер человека. Но и определить его судьбу, показать успех в личной жизни, дать сведения о карьере, расшифровать судьбоносные знаки и даже предсказать будущее. Число имени Геометрия в нумерологии — 1. Девиз имени Геометрия и единиц по жизни: «Я – первый!»
Но и определить его судьбу, показать успех в личной жизни, дать сведения о карьере, расшифровать судьбоносные знаки и даже предсказать будущее. Число имени Геометрия в нумерологии — 1. Девиз имени Геометрия и единиц по жизни: «Я – первый!»
- Планета-покровитель для имени Геометрия — Солнце.
- Знак зодиака для имени Геометрия — Лев и Овен.
- Камни-талисманы для имени Геометрия — аквамарин, берилл, медь, каури, магнит, слюда, мусковит, хризолит, сапфир, песчаник, бирюза.
«Единица» в числах для имени Геометрия – Числе Выражения, Числе Души и Числе внешнего облика – говорит о наличии у человека способностей, обеспечивающих его оригинальность и уникальность. Значение цифры 1 — для имени Геометрия, это прежде всего, способность находить пути и способы самореализации, принципиально отличающиеся от общеизвестных. Обладатели имени Геометрия свободолюбивы, часто эгоистичны. Такие люди стремятся к независимости, вкладывают силы в саморазвитие и реализацию себя.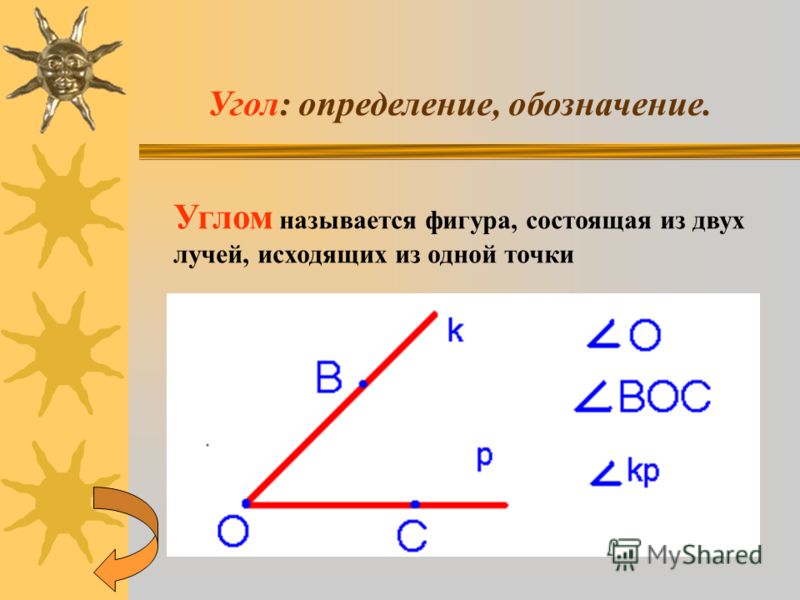 Способность направлять неуемную энергию в нужное русло поможет единицам добиться больших успехов в жизни. Среди них много творческих натур, активных и нуждающихся в постоянном движении вперед. Единица в имени Геометрия — это число лидера. Имя Геометрия обладает мощной энергией, имеет множество идей, которые пытается воплотить самостоятельно. Человек — Единица (Геометрия) имеет силу воли, харизму, держит свое слово, умело решает проблемы других людей. Его нельзя не заметить. Яркий индивидуалист с гипертрофированным эго. Геометрия часто ошибается в личной жизни, нередки разводы. Единица с именем Геометрия не должна быть агрессивной, злиться, иначе она разрушает свое здоровье и выстроенный ранее путь. Порадовать владельца имени Геометрия можно, дав ему уважение, постоянно отмечать его успехи и заслуги.
Способность направлять неуемную энергию в нужное русло поможет единицам добиться больших успехов в жизни. Среди них много творческих натур, активных и нуждающихся в постоянном движении вперед. Единица в имени Геометрия — это число лидера. Имя Геометрия обладает мощной энергией, имеет множество идей, которые пытается воплотить самостоятельно. Человек — Единица (Геометрия) имеет силу воли, харизму, держит свое слово, умело решает проблемы других людей. Его нельзя не заметить. Яркий индивидуалист с гипертрофированным эго. Геометрия часто ошибается в личной жизни, нередки разводы. Единица с именем Геометрия не должна быть агрессивной, злиться, иначе она разрушает свое здоровье и выстроенный ранее путь. Порадовать владельца имени Геометрия можно, дав ему уважение, постоянно отмечать его успехи и заслуги.
- Влияние имени Геометрия на профессию и карьеру. Что значит число 1 в имени Геометрия при выборе сферы деятельности? «Единица» в нумерологическом ядре – это практически всегда потенциально высокий уровень профессионализма.
 Но профессионализма совершенно особого толка – узконаправленного, избирательного, а иногда – единственного в своем роде. Подходящие профессии для имени Геометрия: менеджер, руководитель, предприниматель.
Но профессионализма совершенно особого толка – узконаправленного, избирательного, а иногда – единственного в своем роде. Подходящие профессии для имени Геометрия: менеджер, руководитель, предприниматель. - Влияние имени Геометрия на личную жизнь. Межгендерные отношения – это сфера, в которой положительные и отрицательные проявления личности настолько видоизменены, что дифференцировать их довольно сложно. В частности, число один для имени Геометрия наделяет своего обладателя импульсивностью, хвастовством и самоуверенностью. Эти черты характера для обладателя имени Геометрия обычно считаются недостатками, но «в делах любовных» часто выглядят неотразимыми достоинствами. А склонность к логическим построениям и твердость убеждений – вполне могут быть расценены, как излишняя осторожность и занудство. Единица – символ лидерства, а лидеры по имени Геометрия чаще всего ищут в отношениях заботу и тепло. Более всего им подходят активные тройки, семерки, девятки, а также спокойные двойки и шестерки.

Планета покровитель имени Геометрия
Число 1 для имени Геометрия означает планету Солнце. Единица для имени Геометрия – это изначальное, источник всего. Это число входите состав любого другого числа. Люди с именем Геометрия, чьей планетой-покровителем является Солнце, по натуре очень сильные личности, как правило – лидеры. Им свойственна импульсивность, они никогда не останутся незамеченными. Они добиваются успехов практически в любом деле. Людям Солнца по имени Геометрия присущи такие черты характера, как стремление к власти, великодушие, справедливость, ответственность, инициативность. Гармоничные отношения у этой категории сложатся с людьми этой же группы.
Знаки зодиака имени Геометрия
Для имени Геометрия подходят следующие знаки зодиака:
 Обладатели имени Геометрия ненавидят любые ограничения. К себе относятся требовательно, придирчивы ко внешности, поэтому уделяют ей много внимания. Львы с именем Геометрия стараются произвести на людей благоприятное впечатление, любят нравиться. Попал в милость ко Льву – считай, повезло. Тебя будут превозносить, везде брать с собой (чтобы похвастаться) и учить манерам – аристократы еще те. А вот ругаться со Львом по имени Геометрия не рекомендуется: они остры на язык и за словом в карман не полезут. Через пять минут будешь стоять с красными от злости щеками и негодовать, какого черта он смеет с тобой так разговаривать? Причем Лев Геометрия врать не станет – скажет мало, четко и по делу. С противной ухмылкой. Так что еще сам останешься виноват и в депрессии на тему «куда катится моя жизнь». Владельцы имени Геометрия жуткие эгоцентрики – обожают комплименты, быть в центре внимания и подарки (хотя им больше нравится слово «подношения»).
Обладатели имени Геометрия ненавидят любые ограничения. К себе относятся требовательно, придирчивы ко внешности, поэтому уделяют ей много внимания. Львы с именем Геометрия стараются произвести на людей благоприятное впечатление, любят нравиться. Попал в милость ко Льву – считай, повезло. Тебя будут превозносить, везде брать с собой (чтобы похвастаться) и учить манерам – аристократы еще те. А вот ругаться со Львом по имени Геометрия не рекомендуется: они остры на язык и за словом в карман не полезут. Через пять минут будешь стоять с красными от злости щеками и негодовать, какого черта он смеет с тобой так разговаривать? Причем Лев Геометрия врать не станет – скажет мало, четко и по делу. С противной ухмылкой. Так что еще сам останешься виноват и в депрессии на тему «куда катится моя жизнь». Владельцы имени Геометрия жуткие эгоцентрики – обожают комплименты, быть в центре внимания и подарки (хотя им больше нравится слово «подношения»). По-простому, баран. Обладалели имени Геометрия — самые упертые люди в мире. Даже если ты уже доказал им свою правоту и они в нее поверили, все равно будут уверять, что это они в белом пальто, а дебил тут ты. Переспорить невозможно, лучше даже не пытаться, сбереги свои нервные клетки, покивай головой на его ахинею и отойди в сторонку. Ненавидят конкуренцию: если кто-то в окружении Овна Геометрия будет в чем-то лучше него, то тот костьми ляжет, но сделает так, чтобы утереть противнику нос.
По-простому, баран. Обладалели имени Геометрия — самые упертые люди в мире. Даже если ты уже доказал им свою правоту и они в нее поверили, все равно будут уверять, что это они в белом пальто, а дебил тут ты. Переспорить невозможно, лучше даже не пытаться, сбереги свои нервные клетки, покивай головой на его ахинею и отойди в сторонку. Ненавидят конкуренцию: если кто-то в окружении Овна Геометрия будет в чем-то лучше него, то тот костьми ляжет, но сделает так, чтобы утереть противнику нос.Цвет имени Геометрия
Красный цвет имени Геометрия. Люди с именем Геометрия, носящие красный цвет, очень добрые и отзывчивые, они всегда придут на помощь, но будут ждать ответной реакции. И если она не последует, то, возможно, серьёзно обидятся, но не покажут этого, просто отдалятся от человека на некоторое время. Среди обладателей имени Геометрия много лидеров, ведущих до конца к цели, требуя от ведомых полной отдачи, из-за чего часто их и недолюбливают. Носители имени Геометрия верные друзья, но, увы, друзей у них не так уж и много. Положительные черты характера для людей с именем Геометрия – доброта, отзывчивость, лидерство. Отрицательные черты характера для людей с именем Геометрия – эгоистичность, нетерпимость к порокам других.
Положительные черты характера для людей с именем Геометрия – доброта, отзывчивость, лидерство. Отрицательные черты характера для людей с именем Геометрия – эгоистичность, нетерпимость к порокам других.
Как правильно пишется имя Геометрия
В русском языке грамотным написанием этого имени является — Геометрия. В английском языке имя Геометрия может иметь следующий вариант написания — Geometriya.
Склонение имени Геометрия по падежам
| Падеж | Вопрос | Имя |
| Именительный | Кто? | Геометрия |
| Родительный | Нет Кого? | Геометрии |
| Дательный | Рад Кому? | Геометрии |
| Винительный | Вижу Кого? | Геометрию |
| Творительный | Доволен Кем? | Геометрией |
| Предложный | Думаю О ком? | Геометрии |
Видео значение имени Геометрия
Как узнать своё число имени по буквице?» src=»https://www.youtube.com/embed/znAhBkmkCBs?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Вы согласны с описанием и значением имени Геометрия? Какую судьбу, характер и национальность имеют ваши знакомые с именем Геометрия? Каких известных и успешных людей с именем Геометрия вы еще знаете? Будем рады обсудить имя Геометрия более подробно с посетителями нашего сайта в комментариях ниже.
Если вы нашли ошибку в описании имени, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Геометрические символы
Все геометрические символы, которые я мог придумать, собраны на этой странице. Если вы не нашли символ, который искали, пожалуйста, напишите по электронной почте, и я добавлю его в этот список.
Символы Значение символов
Следовательно,
Если x, то y
конгруэнтно
не конгруэнтно
аналогично
Угол с вершиной A
относится к углам )
Измерение угла A в градусах
° Градусах
n ° n градусах
Перпендикулярно
не перпендикулярно
|| параллельно
не параллельно
∟ знак прямого угла
∆ABC Треугольники с вершинами A, B и C;
обозначает треугольники (более одного)
Параллелограмм с вершинами A, B, C и D
обозначает параллелограммы (более одного)
круг с центром A
Сегмент AB с конечными точками A и B
AB Длина отрезка AB
Луч AB с конечной точкой A, проходящей через точку B
Прямая, проходящая через точки A и B
π Отношение длины окружности к диаметру окружности.
с Обычно Длина стороны
b длина основания
A Площадь
h высота фигуры
d диаметр окружности
r радиус окружности
P периметр
C окружность
B Площадь основания
л.A. Боковое пространство
Площадь поверхности SA
Объем V
л наклонная высота
a апофема
b 1 , b 2 основания трапеции (параллельные стороны)
n-угольник с n сторонами
Дуга с конечными точками A и B
Дуга с конечными точками A и C, содержащая B
Дуга AB
Список геометрии и тригонома попробуйте Символы
Геометрия и тригонометрия — это разделы математики, связанные с геометрическими фигурами и углами треугольников.В следующем списке представлены некоторые из наиболее примечательных символов в этих темах, а также их использование и значение.
Для удобства чтения эти символы сгруппированы по их функции в таблицы. Другие исчерпывающие списки математических символов — с разбивкой по предметам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Другие исчерпывающие списки математических символов — с разбивкой по предметам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Предпочитаете версию в формате PDF?
Получите общую сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Символы, связанные с точками / линиями
В геометрии точек и линий образуют основу более сложных геометрических фигур, таких как треугольники, окружности, четырехугольники и многоугольники. В следующей таблице приведены некоторые из наиболее примечательных символов, связанных с ними, а также их значение и пример.
| Название символа | Пояснение | Пример |
|---|---|---|
| $ A $, $ B $, $ C $, $ D $, $ P $, $ Q $, $ R $, $ S $ | Переменные для точек | Если $ P_1 = P_2 $, то $ \ overline {P_1 Q} = \ overline {P_2 Q} $. |
| $ \ ell $ | Переменная для линий | $ \ ell_1 \ parallel \ ell_2 $ |
| $ \ overleftrightarrow {AB} $ | $(Бесконечная) линия $ A и $ B $ | $ \ overleftrightarrow {AB} = \ overleftrightarrow {BA} $ |
| $ \ overline {AB} $ | Отрезок линии между точками $ A $ и $ B $ | $ \ overline {AB} \ cong \ overline {PQ} $ |
| $ \ overrightarrow {AB} $ | Луч из точки $ A $ в точку $ B $ | $ \ overrightarrow {AB} \ ne \ overrightarrow { BA} $ |
| $ | AB | $ | Расстояние от точки $ A $ до точки $ B $ | $ | BC | \ le \\ | AB | + | AC | $ |
| $ \ ell_1 \ parallel \ ell_2 $ | Линии $ \ ell_1 $ и $ \ ell_2 $ параллельны | Если $ \ square ABCD $ — параллелограмм, то $ \ overline { AB} \ parallel \ overline {CD} $. 2. $ 2. $ |
| $ \ ell_1 \ not \ perp \ ell_2 $ | Линии $ \ ell_1 $ и $ \ ell_2 $ не перпендикулярны | Если $ \ overline {AB} \ not \ perp \ overline {BC} $, тогда $ \ square ABCD $ не является прямоугольником. |
Угловые символы
Угол по существу соответствует «раскрытию» геометрической фигуры, количественная оценка которой ведет к значительному развитию геометрии и тригонометрии. В следующей таблице приведены некоторые из наиболее известных символов, относящихся к углам, а также их значение и пример.{\ prime \ prime} = \ left (\ dfrac {38} {60} \ right) ‘$
Символы, относящиеся к кругу
Окружность может рассматриваться как набор всех точек, равноотстоящих от данного точка, и часто играет решающую роль в развитии евклидовой геометрии и тригонометрии. В следующей таблице приведены некоторые из наиболее примечательных символов, связанных с кругом, с их соответствующим значением и примером.
В следующей таблице приведены некоторые из наиболее примечательных символов, связанных с кругом, с их соответствующим значением и примером.
| Название символа | Объяснение | Пример | ||
|---|---|---|---|---|
| $ O $ | Переменная для круга (или центр круга ) | $ O $ O_2, если круги $ O_2 одинакового радиуса, то они конгруэнтны. | ||
| $ \ odot P $ | Окружность с центром вокруг точки $ P $ | Если $ P \ ne Q $, то $ \ odot P \ ne \ odot Q $. | ||
| $ r $ | Радиус окружности | $ r = \ sqrt {\ dfrac {A} {\ pi}} $ | ||
| $ d $ | Диаметр окружности | $ d = 2r $ | ||
| $ C $ | Окружность окружности | $ C = 2 \ pi r $ | ||
| $ \ overparen {AB} $ | Сегмент дуги между точками $ A $ и $ B $ | Если $ \ overline {AB} $ — диаметр, то $ \ overparen {AB} $ будет соответствовать полуокружности. {- 1} x $ {- 1} x $ | Функция арктангенса (Арктангенс) | $ \ displaystyle \ lim_ {x \ to \ infty} \ arctan x = \ dfrac {\ pi} {2} $ |
Другие символы, связанные с 2D / 3D-фигурами
В элементарной геометрии большая часть исследования вращается вокруг анализа многоугольников , многогранников и других трехмерных фигур .В следующей таблице приведены некоторые из наиболее примечательных символов в этих категориях, а также их значение и использование.
| Название символа | Пояснение | Пример |
|---|---|---|
| $ \ треугольник ABC $ | Треугольник с вершинами $ A $, $ B $ и $ C $ | $ \ треугольник \ треугольник A’B’C ‘$ |
| $ \ square ABCD $ | Квадрат / Четырехугольники с вершинами $ A $, $ B $, $ C $ и $ D $ | If $ \ overline {AB} \ parallel \ overline {CD} $, тогда $ \ square ABCD $ — трапеция. |
| $ \ Pi $ (Заглавная пи) | Переменная для плоскостей | $ \ Pi_1 \ parallel \ Pi_2 $ |
| $ F \ sim F ‘$ | Рисунок $ F $ равен аналогично к фигуре $ F ‘$ | $ \ треугольник ABC \ sim \ треугольник PQR $ |
| $ F \ nsim F’ $ | Рисунок $ F $ не похож на фигуру $ F ‘$ | Поскольку $ F $ — правильный пятиугольник, а $ F ‘$ — нет, $ F \ nsim F’ $. |
| $ F \ cong F ‘$ | Рисунок $ F $ соответствует фигуре $ F’ $ | $ \ треугольник ABC \ cong \ треугольник A’B’C ‘$ $ \ implies \ overline {AB} \ cong \ overline {A’B ‘} $ |
| $ F \ ncong F’ $ | Рисунок $ F $ не соответствует рисунку $ F ‘$ | $ \ square ABCD \ nsim \\ \ square A’B’C’D ‘\ подразумевает \\ \ square ABCD \ ncong \\ \ square A’B’C’D’ $ |
| $ \ varphi $ (phi) | Золотое сечение | $ \ varphi = \ dfrac {1 + \ sqrt {5}} {2} \ приблизительно 1.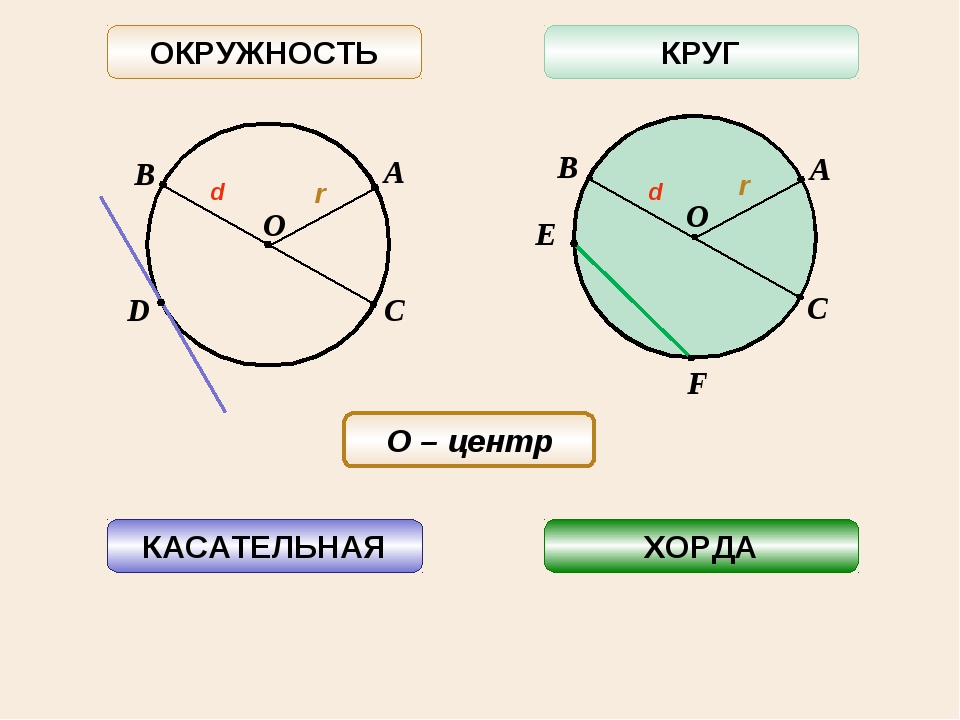 618 $ 618 $ |
| $ h $ | Высота треугольника / четырехугольника / 3D-фигур | Поскольку $ h = 5 $, $ A = \ dfrac {5 \ cdot 3} {2} $. |
| $ b $ | Основание треугольника / четырехугольника | Для тупого треугольника $ b $ соответствует расширенному основанию треугольника. |
| $ l $ | Длина прямоугольника / сплошного прямоугольника | Когда $ l = 10 $, $ A = 10 \ cdot 20 $. |
| $ w $ | Ширина прямоугольника / сплошного прямоугольника | $ A = lw $ |
| $ P $ | Периметр плоской фигуры | Для прямоугольника + $ P = 2 2w $. |
| $ A $ | Площадь плоской фигуры (или площадь поверхности 3D-фигуры) | Для треугольника $ A = \ dfrac {bh} {2} $. |
| $ V $ | Объем трехмерной фигуры | Для сферы $ V \ propto r ^ 3 $. {\ circ} $. {\ circ} $. |
| $ V $ | Количество вершин в многограннике | Для куба $ V = 8 $. |
| $ E $ | Количество ребер в многограннике | В общем, $ E \ ge V $ для многогранников. |
| $ F $ | Количество граней в многограннике | Для тетраэдра $ F = 4 $. |
| $ \ chi $ (chi) | Эйлерова характеристика | Для выпуклых многогранников $ \ chi = V-E + F = \\ 2.$ |
На следующих рисунках показаны 5 платоновых тел (правильные, выпуклые многогранники) вместе с их соответствующим количеством вершин, ребер и граней.
- Тетраэдр $ (V = 4, E = 6, \\ F = 4, \ chi = 2) $
- Куб $ (V = 8, E = 12, \\ F = 6, \ chi = 2) $
- Октаэдр $ (V = 6, E = 12, \\ F = 8, \ chi = 2) $
- Додекаэдр $ (V = 20, E = 30, F = 12 , \ chi = 2) $
- Икосаэдр $ (V = 12, E = 30, F = 20, \ chi = 2) $
Для основного списка символов см. математические символы.Список символов, разделенных на категории тип и предмет , см. На соответствующих страницах ниже.
математические символы.Список символов, разделенных на категории тип и предмет , см. На соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите общую сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Дополнительные ресурсы
Обозначения и символы в плоской геометрии — видео и стенограмма урока
Линейные отношения
Параллельные линии — это линии, которые никогда не пересекаются и не пересекаются. Перпендикулярные линии пересекаются под прямым углом. Вместо того, чтобы записывать слова «параллельный» и «перпендикулярный», мы используем геометрические обозначения.
Символ для двух параллельных линий — две вертикальные линии.
Символ для двух перпендикулярных линий — это перевернутая буква T.
Части линии
Линейный сегмент — это участок линии между двумя конечными точками.![]() Чтобы обозначить сегмент линии, укажите две конечные точки и поместите символ сегмента над ними.
Чтобы обозначить сегмент линии, укажите две конечные точки и поместите символ сегмента над ними.
Другая часть линии называется лучом. ray имеет одну конечную точку и продолжается в одном направлении вечно. Чтобы выразить это, используйте первую букву как конечную точку, а вторую букву как любую точку дальше по лучу.
На этом изображении луч AB не совпадает с лучом BA , потому что у них две разные конечные точки.
Геометрические фигуры
Плоскость — это плоская поверхность, существующая в пространстве. Думайте о плоскости как о потолке, полу или стене комнаты. Самолеты могут пересекаться друг с другом или никогда не соприкасаться. Плоскость названа с использованием трех неколлинеарных точек , что означает, что невозможно провести линию через точки.
Углы образованы двумя лучами с одинаковой конечной точкой.Все углы имеют вершину , которая является конечной точкой двух лучей. Если в вершине есть только один угол, мы можем определить угол, используя одну заглавную букву, где точка вершины — это имя угла. Мы также можем определить угол, используя три заглавные буквы, где первая и третья буквы — это точки на лучах, образующих углы, а вторая буква — вершина. Третий способ определить угол — вставить число внутри угла.
Мы можем определить следующий угол четырьмя различными способами, но мы всегда помещаем символ угла перед идентифицирующими буквами.
Чтобы определить треугольник, нарисуйте треугольник перед тремя вершинами треугольника.
Единицы измерения
Когда дело доходит до единиц измерения, длина сегмента может быть выражена как две конечные точки сегмента без символа над ним.
При обсуждении меры угла поместите м перед символом угла, чтобы показать эту меру.
Конгруэнтные фигуры имеют одинаковый размер и форму. Углы двух равных треугольников равны. Хотя углы равны, меры равны. Конгруэнтность относится к формам, а равенство — к числам.
Обратите внимание, как символ сравнения имеет волнистую линию над знаком равенства.
Символ равенства — это просто знак равенства.
Длины сторон двух равных треугольников равны. Однако стороны не равны; вместо этого стороны совпадают.
Резюме урока
Давайте рассмотрим. Целью геометрического обозначения является идентификация геометрических фигур или форм и размеров этих фигур, таких как их длина или размеры.Вот список всех геометрических обозначений, обсуждаемых в этом уроке.
Целью геометрического обозначения является идентификация геометрических фигур или форм и размеров этих фигур, таких как их длина или размеры.Вот список всех геометрических обозначений, обсуждаемых в этом уроке.
математических символов и их значение
Математические символы — часто крошечные, неразборчивые и кажущиеся случайными — очень важны. Некоторые математические символы представляют собой греческие и латинские буквы, восходящие к древним временам. Другие, такие как знаки плюса, минуса, времени и деления, кажутся простыми обозначениями на бумаге. Тем не менее, символы в математике — это, по сути, инструкции, которыми руководствуются ученые в этой области.И они имеют настоящую ценность в реальной жизни.
Знак «плюс» (+) может сказать вам, добавляете ли вы наличные на свой банковский счет, а знак «минус» (-) может указывать на предстоящие проблемы — что вы вычитаете средства и, возможно, рискуете исчерпать деньги.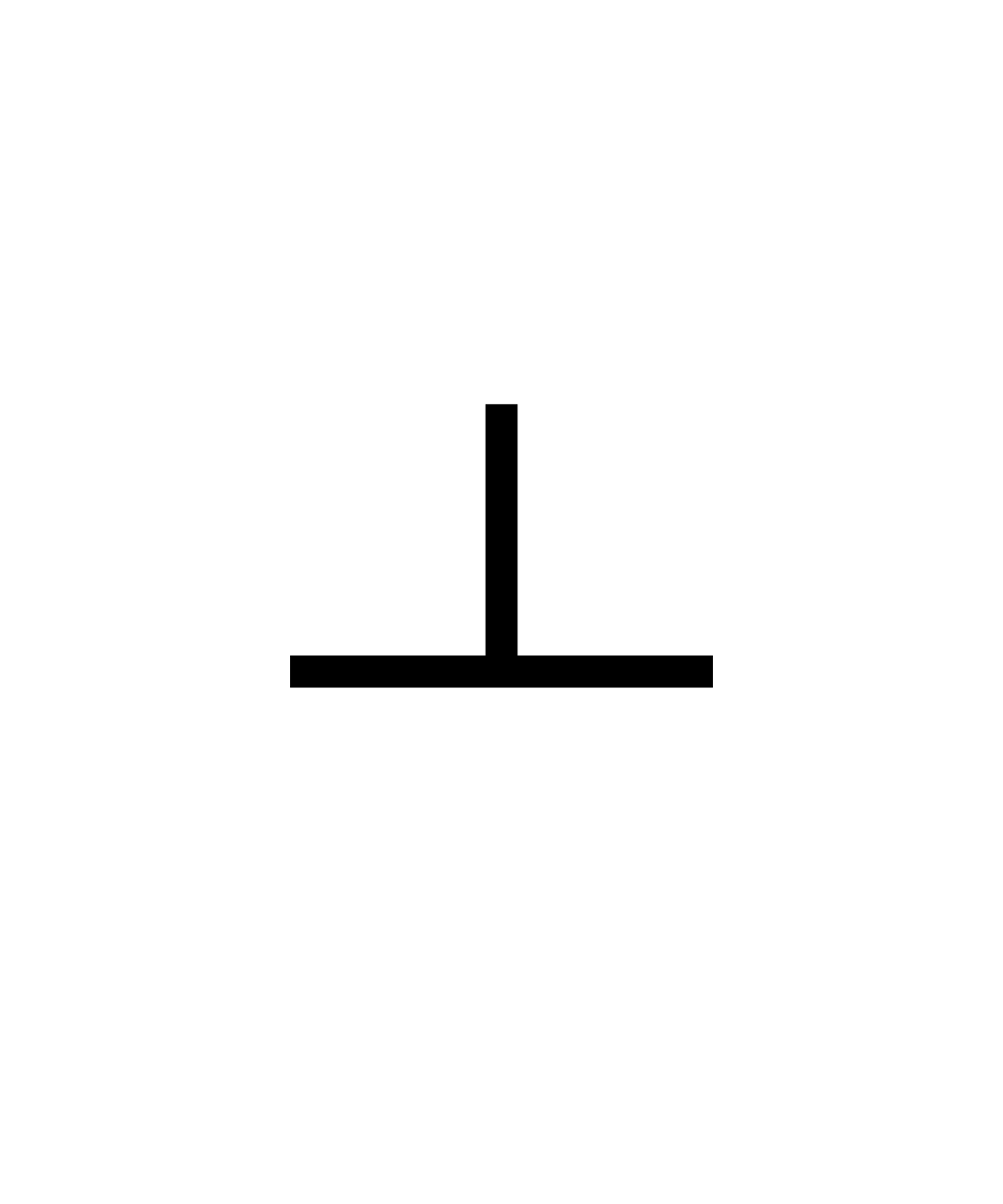 Круглые скобки, которые в английской пунктуации указывают на то, что вы вставляете несущественную мысль в предложение, в математике означают прямо противоположное: сначала вы должны проработать то, что находится внутри этих двух знаков препинания, и только потом решать остальную задачу.Прочтите, чтобы узнать, что такое общие математические символы, что они представляют и почему они важны.
Круглые скобки, которые в английской пунктуации указывают на то, что вы вставляете несущественную мысль в предложение, в математике означают прямо противоположное: сначала вы должны проработать то, что находится внутри этих двух знаков препинания, и только потом решать остальную задачу.Прочтите, чтобы узнать, что такое общие математические символы, что они представляют и почему они важны.
Общие математические символы
Вот список наиболее распространенных символов, используемых в математике.
Символ | Что представляет собой |
| + | Добавляющий знак: часто обозначается как знак «плюс» или «знак сложения». |
| — | Знак вычитания: часто обозначается как знак минус |
| х | Знак умножения: часто упоминается как знак умножения или таблицы умножения |
| ÷ | Знак деления: Разделить |
| = | Знак равенства |
| | | | Абсолютное значение |
| ≠ | Не равно |
| () | Круглая скобка |
| [] | Квадратные скобки |
| % | Знак процента: Из 100 |
| ∑ | Знак большой суммы: суммирование |
| √ | Знак квадратного корня |
| < | Знак неравенства: менее |
| > | Знак неравенства: больше |
| ! | Факториал |
| θ | Тета |
| π | Пи |
| ≅ | Примерно |
| ∅ | Пустой набор |
| ∠ | Угловой знак |
| ! | Факторный знак |
| ∴ | Следовательно |
| ∞ | бесконечность |
Математические символы в реальной жизни
Вы используете математические символы чаще, чем думаете, во всех сферах своей жизни. Как отмечалось выше, разница между символом плюса и минуса в банковском деле может указывать на то, добавляете ли вы большое количество средств на свой банковский счет или снимаете средства. Если вы когда-либо использовали электронную таблицу бухгалтерского учета, вы, вероятно, знаете, что знак большой суммы (∑) дает вам простой — действительно мгновенный — способ добавить бесконечный столбец чисел.
Как отмечалось выше, разница между символом плюса и минуса в банковском деле может указывать на то, добавляете ли вы большое количество средств на свой банковский счет или снимаете средства. Если вы когда-либо использовали электронную таблицу бухгалтерского учета, вы, вероятно, знаете, что знак большой суммы (∑) дает вам простой — действительно мгновенный — способ добавить бесконечный столбец чисел.
«Пи», обозначаемое греческой буквой π, используется во всем мире математики, науки, физики, архитектуры и других сфер. Несмотря на происхождение числа пи в предмете геометрии, это число находит применение во всей математике и даже проявляется в предметах статистики и вероятности.А символ бесконечности (∞) не только является важным математическим понятием, но также предполагает бесконечные просторы Вселенной (в астрономии) или бесконечные возможности, которые исходят от каждого действия или мысли (в философии).
Советы по символам
Хотя в этом списке указано больше математических символов, это одни из наиболее распространенных.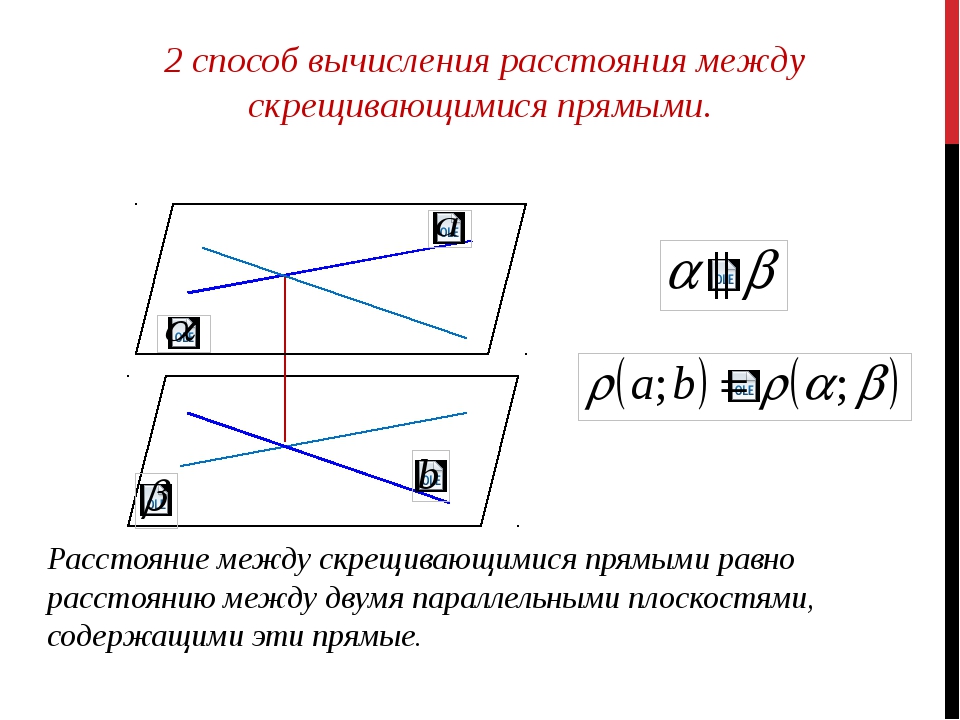 Вам часто потребуется использовать HTML-код, чтобы символы отображались в Интернете, поскольку многие шрифты не поддерживают использование математических символов.Однако вы также найдете большинство из них на графическом калькуляторе.
Вам часто потребуется использовать HTML-код, чтобы символы отображались в Интернете, поскольку многие шрифты не поддерживают использование математических символов.Однако вы также найдете большинство из них на графическом калькуляторе.
По мере вашего прогресса в математике вы начнете использовать эти символы все больше и больше. Если вы планируете изучать математику, это будет стоить вашего времени — и действительно сэкономит вам бесконечное (∞) количество этого ценного ресурса — если вы держите эту таблицу математических символов под рукой.
перпендикулярных линий
Перпендикулярные линии линии, сегменты или лучи которые пересекаются, образуя прямые углы.
Символ ⊥ означает перпендикулярно .
На рисунке
п р ⊥ Q S
Символ прямого угла на рисунке означает, что линии перпендикулярны.
В трех измерениях у вас может быть три линии, которые взаимно перпендикулярны.
Лучи п Т → , Т U → и Т W → перпендикулярны друг другу.
Пример :
Если А B ⊥ C D , найти м ∠ E О D .
С А B ⊥ C D , м ∠ B О D знак равно 90 ° .
Согласно постулату сложения углов,
м ∠ B О E + м ∠ E О D знак равно м ∠ B О D
Позволять
Икс
°
быть мерой
∠
E
О
D
.
Затем,
35 год ° + Икс ° знак равно 90 ° .
Вычесть 35 год ° с каждой стороны.
Икс ° знак равно 55 °
Следовательно,
м ∠ E О D знак равно 55 ° .
Nemeth Tutorial — Урок 4.5
Символы
и xutri; треугольник
⠫⠞
∠ угол
⠫⠪
индикатор пунктуации
⠸
Основные геометрические символы
Пояснение
Использование профилей
Математики разработали тип стенографии, включающий символы, знаки и сокращения, которые используются во всем мире. Такое использование позволяет математикам, ученым, инженерам, исследователям и другим специалистам во многих других областях иметь возможность общаться на разных языках и культурах, используя определенные согласованные символы. Поэтому символы, используемые в математике, лаконичны и имеют конкретное применение.
Поэтому символы, используемые в математике, лаконичны и имеют конкретное применение.
Формы используются для обозначения особых значений. Чаще всего форма используется для представления именно этого: миниатюрной формы или изображения, например геометрической формы. Эти миниатюрные фигуры не используются вместо обозначенных диаграмм. Символ формы должен использоваться только тогда, когда соответствующий миниатюрный символ формы используется в печатной продукции. Другое использование — нанесение символов формы аналогично другим математическим символам, например, использование их в качестве знаков операции или знаков сравнения.Часто символ фигуры комбинируется с другим символом, например, минусом, плюсом или знаком умножения. Символы формы также могут использоваться для обозначения пропущенных элементов или в качестве держателей замещающих значений во многом таким же образом, как общий символ пропуска представляет пропущенный элемент.
Индикатор формы является уникальным для шрифта Брайля и состоит из точек один-два-четыре-шесть.
Применение индикатора формы
Брайль включает использование индикатора формы, точки один, два, четыре, шесть, чтобы указать, что символ или символы, следующие за ним, представляют форму.Индикатор формы не имеет соответствующего напечатанного символа; он используется, чтобы указать, что фигура появляется в печати. Индикатор формы — это первый символ в серии символов Брайля, за исключением тех случаев, когда печатный символ отображается отмененным знаком отрицания, например косой чертой или вертикальной полосой. Буква или буквы, цифра или символы, указывающие на форму, помещаются в ячейки Брайля сразу после индикатора формы. Знак формы должен располагаться с интервалом в соответствии с заданным значением формы.Если, например, он представляет собой пропущенный знак операции, он будет размещен в соответствии с правилами для знаков пропуска.
Двухклеточные формы: буква или буквы предполагают форму
Многие символы фигур отображаются с индикатором формы, за которым следует буква или буквы, указывающие на форму. Сочетание индикатора формы с другими буквами позволяет отображать различные формы шрифтом Брайля. Индикатор формы, за которым следует буква s, представляет собой звезду. Индикатор формы, за которым следует буква t, представляет собой треугольник.Индикатор формы, за которым следуют точки два-четыре-шесть, представляет собой символ угла.
Сочетание индикатора формы с другими буквами позволяет отображать различные формы шрифтом Брайля. Индикатор формы, за которым следует буква s, представляет собой звезду. Индикатор формы, за которым следует буква t, представляет собой треугольник.Индикатор формы, за которым следуют точки два-четыре-шесть, представляет собой символ угла.
Интервал со знаками фигур
Фигурный символ, обозначающий букву или буквы, цифру или цифры, должен отделяться от идентифицированного символа или символов пробелом. Знаки формы — математические символы. Пунктуация должна выполняться в соответствии с инструкциями по нанесению знаков препинания математическим символам. В частности, когда формы образуются множественным числом или притяжательным числом с апострофом, индикатор пунктуации вставляется без пробела между знаком формы и апострофом.
Когда знак формы имеет множественное число или притяжательное окончание, знак формы и связанное с ним пространство прерываются и больше не считаются единым целым. Буква или буквы, следующие за пробелом после; s или апострофа, поэтому не считаются частью идентифицированного знака формы. Буква или буквы, идентифицирующие форму, следующие за индикатором формы, символом формы и; s или апострофом; s, будут набираться шрифтом в соответствии с правилами использования и неиспользования индикатора английской буквы.То есть для одной буквы требуется индикатор с английской буквой. Для двух или более букв в серии не требуется индикатор английской буквы.
Буква или буквы, следующие за пробелом после; s или апострофа, поэтому не считаются частью идентифицированного знака формы. Буква или буквы, идентифицирующие форму, следующие за индикатором формы, символом формы и; s или апострофом; s, будут набираться шрифтом в соответствии с правилами использования и неиспользования индикатора английской буквы.То есть для одной буквы требуется индикатор с английской буквой. Для двух или более букв в серии не требуется индикатор английской буквы.
Пример 1
& xutri; ABC
⠫⠞⠀⠠⠁⠠⠃⠠⠉
Пример 2
△ A
Пример 3
∠1
Пример 4
∠MNO
⠫⠪⠀⠠⠍⠠⠝⠠⠕
Пример 5
A & xutri; имеет три стороны.
⠠⠁⠀⠫⠞⠀⠓⠁⠎⠀⠞⠓⠗⠑⠑⠀⠎⠊⠙⠑⠎⠲
Пример 6
До появления UEB индикатор пунктуации широко использовался, поскольку в Nemeth он должен располагаться между любой литературной пунктуацией и математическим символом.Однако с UEB такие ситуации возникают редко, поскольку режим Nemeth обычно завершается до знаков препинания. Таким образом, это руководство не будет подробно охватывать индикатор пунктуации, но ниже приведен пример его использования.
Таким образом, это руководство не будет подробно охватывать индикатор пунктуации, но ниже приведен пример его использования.
Являются ли & xutri; ‘sAandBacute?
⠠⠁⠗⠑⠀⠸⠩⠀⠫⠞⠸⠄⠎⠀⠰⠠⠁⠀⠠⠄⠁⠝⠙⠀⠰⠠⠃⠀⠸⠱⠀⠁⠉⠥⠞⠑⠦
Пример 7
& xutri; sABCandDEF
⠸⠩⠀⠫⠞⠎⠀⠠⠁⠠⠃⠠⠉⠀⠠⠄⠁⠝⠙⠀⠠⠙⠠⠑⠠⠋⠀⠸⠱
Пример 8
(с признаками сравнения) ∠1 = 85 °
⠫⠪⠀⠼⠂⠀⠨⠅⠀⠼⠦⠢⠘⠨⠡
Пример 9
∠ABC = 100 °
⠫⠪⠀⠠⠁⠠⠃⠠⠉⠀⠨⠅⠀⠼⠂⠴⠴⠘⠨⠡
Пример 10
(с операциями) ∠1 + ∠2
⠫⠪⠀⠼⠂⠬⠫⠪⠀⠼⠆
Пример 11
∠ABC> ∠XYZ
⠫⠪⠀⠠⠁⠠⠃⠠⠉⠀⠨⠂⠀⠫⠪⠀⠠⠭⠠⠽⠠⠵
предыдущая — следующая (упражнения)
Примечание: доступность веб-сайтов APH
% PDF-1.5
%
52 0 obj>
эндобдж
xref
52 74
0000000016 00000 н.
0000002082 00000 н.
0000001776 00000 н.
0000002182 00000 п.
0000002377 00000 н.
0000003182 00000 н.
0000003621 00000 н.
0000003975 00000 н.
0000004009 00000 н.
0000004236 00000 п.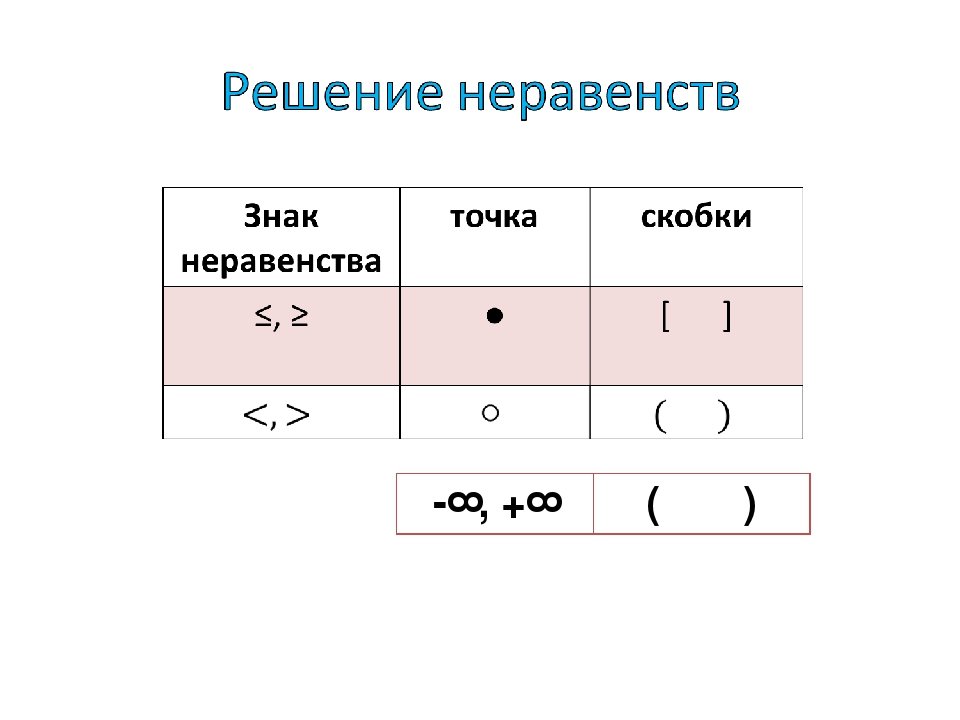 0000004457 00000 н.
0000004533 00000 н.
0000005563 00000 н.
0000006311 00000 н.
0000007202 00000 н.
0000008416 00000 н.
0000009535 00000 н.
0000010663 00000 п.
0000011712 00000 п.
0000012899 00000 н.
0000015568 00000 п.
0000015835 00000 п.
0000016072 00000 п.
0000016322 00000 п.
0000016551 00000 п.
0000016809 00000 п.
0000017019 00000 п.
0000017304 00000 п.
0000017549 00000 п.
0000017782 00000 п.
0000018050 00000 п.
0000018319 00000 п.
0000018585 00000 п.
0000018813 00000 п.
0000019045 00000 п.
0000019278 00000 п.
0000019496 00000 п.
0000019725 00000 п.
0000019954 00000 п.
0000020186 00000 п.
0000020413 00000 п.
0000020714 00000 п.
0000020967 00000 п.
0000021219 00000 п.
0000021444 00000 п.
0000021686 00000 п.
0000021898 00000 п.
0000022132 00000 п.
0000022364 00000 п.
0000022605 00000 п.
0000022814 00000 п.
0000023083 00000 п.
0000023295 00000 п.
0000023572 00000 п.
0000023818 00000 п.
0000024100 00000 п.
0000024356 00000 п.
0000024586 00000 п.
0000004457 00000 н.
0000004533 00000 н.
0000005563 00000 н.
0000006311 00000 н.
0000007202 00000 н.
0000008416 00000 н.
0000009535 00000 н.
0000010663 00000 п.
0000011712 00000 п.
0000012899 00000 н.
0000015568 00000 п.
0000015835 00000 п.
0000016072 00000 п.
0000016322 00000 п.
0000016551 00000 п.
0000016809 00000 п.
0000017019 00000 п.
0000017304 00000 п.
0000017549 00000 п.
0000017782 00000 п.
0000018050 00000 п.
0000018319 00000 п.
0000018585 00000 п.
0000018813 00000 п.
0000019045 00000 п.
0000019278 00000 п.
0000019496 00000 п.
0000019725 00000 п.
0000019954 00000 п.
0000020186 00000 п.
0000020413 00000 п.
0000020714 00000 п.
0000020967 00000 п.
0000021219 00000 п.
0000021444 00000 п.
0000021686 00000 п.
0000021898 00000 п.
0000022132 00000 п.
0000022364 00000 п.
0000022605 00000 п.
0000022814 00000 п.
0000023083 00000 п.
0000023295 00000 п.
0000023572 00000 п.
0000023818 00000 п.
0000024100 00000 п.
0000024356 00000 п.
0000024586 00000 п.


 Но профессионализма совершенно особого толка – узконаправленного, избирательного, а иногда – единственного в своем роде. Подходящие профессии для имени Геометрия: менеджер, руководитель, предприниматель.
Но профессионализма совершенно особого толка – узконаправленного, избирательного, а иногда – единственного в своем роде. Подходящие профессии для имени Геометрия: менеджер, руководитель, предприниматель.