Геометрические знаки и символы обозначения: Знак совмещения в геометрии

Математические знаки и символы на английском

Основные математические знаки и символы на английском языке (плюс, минус, деление, умножение и другие, менее распространённые знаки и символы).

* — для самостоятельно изучающих английский язык также могут быть интересными разделы «Фильмы на английском» и «Аудиокниги на английском».

 

В данной статье мы рассмотрим наиболее распространенные математические знаки и символы на английском языке. Графическое изображение математических знаков и символов универсально во всех языках, но их звучание и произношение значительно отличаются друг от друга. Если вы работаете за границей или даже просто общаетесь на английском с друзьями, вам необходимо знать произношение основных символов на английском языке.

 

Математические знаки, использующиеся для основных арифметических действий:

«+» — plus — плюс

«-» — subtraction sign – знак вычисления

«x» — multiplication sign – знак умножения

«/»  slash . .. divided by – косая линия. Этот математический символ в английском языке также употребляется в качестве знака деления.

«÷» division sign  — знак деления

«:» — сolon – двоеточие; или ratio sign — знак отношения или деления в английском языке

«=» еqual sign – знак равенства

Эти математические знаки известны всем и употребляются повсеместно, поэтому нужно знать, как они звучат на английском языке.

 

Следующие математические символы не так распространены, но всё же не помешает их знание на английском:

«%» Percent symbol – математический символ в английском языке, который употребляется для обозначения процентов

«[ ]» square brackets – квадратные скобки

«±» рlus/minus sign  — знак плюс/минус

«≈» аpproximate equal sign — приближенное равенство

«<» inequality sign (less than – меньше чем) — знак неравенства

«>» inequality sign (greater than – больше чем) — знак неравенства

« ≤ » inequality sign (less than or equal to . .. — меньше чем или соответствует …)

«{ }» сurly brackets (the quantity …… the set …- общее количество) — фигурные скобки

«√» surd (… root of … – корень из) — иррациональное число

«√» square root – квадратный корень

 

Математические знаки и символы очень разнообразны и отличаются сферой употребления. Ниже перечисленные математические знаки и символы менее распространены и употребляются в основном в специализированных областях. Вот написание ещё нескольких математических символов на английском:

«∫» — integral — интегральный

«i» — imaginary unit — мнимая единица

«z*» — complex conjugate — комплексно сопряжённая величина

«∇» — nabla/del — набла

«δ» — delta function — дельта-функция

«∞» — infinity symbol – символ бесконечности

«∅» null symbol — нуль или  недействительный; несущественный

 

Вот еще несколько математических символов, которые используют в геометрии, которые на английском выглядят следующим образом:

«|» — perpendicular – перпендикулярный

«||» — parallel – параллельный

«≅» — congruent to – соответствующий (эквивалентность геометрических форм и размеров)

«∠» angle symbol – знак, который используют в геометрии для обозначения угла

 

Это лишь небольшой список наиболее употребляемых математических знаков и символов на английском, но, если углубиться в специализированную тематику, можно увидеть еще много знаков и символов, характеризующих различные понятия в данной сфере.

Условные обозначения для векторных слоев—ArcGIS Pro

Если данные находятся в векторном слое, можно изменить способ отображения данных, отобразив с помощью символов векторный слой. ArcGIS Pro предоставляет множество методов символизации, известных как символы, для векторных слоев:

• Единый символ – отрисовывает все пространственные объекты слоя одним и тем же условным знаком.
• Уникальные значения – применяют разные условные знаки к разным группам пространственных объектов на основании одного или нескольких полей.
• Градуированные цвета – показывают количественные различия объектов благодаря спектру цветов.
• Градуированные символы – показывают количественные различия между картографируемыми объектами символами разных размеров.
• Двумерные цвета – используют градуированные цвета для отображения количественных различий в значениях объектов между двумя полями.
• Неклассифицированные цвета – показывают качественные отличия в значениях объектов с помощью цветового спектра, который не разбит на дискретные классы.
• Пропорциональные символы – представляют количественные значения в виде серии неклассифицированных пропорционально масштабированных символов.
• Плотность точек – отображение количеств как точечных символов, распределенных внутри полигонов. Этот метод доступен только для полигональных объектов.
• Диаграммы — отображает количественные значения в нескольких полях с помощью диаграмм.
• Карта интенсивности – отображает плотность точек при помощи непрерывного градиента цвета.
• Словарь – применяет символы к данным с использованием нескольких атрибутов.

Большинством векторных слоев используется один из этих типов символов. В зависимости от типа данных, вы можете выбрать из нескольких или всех типов символов. После применения эти варианты условных обозначений отобразят пространственные объекты слоя символами по умолчанию.

Также можно вернуться из режима форматирования символов на панели Символы, если щелкнуть символ на вкладке Основные символы. В режиме Форматировать символ есть две вкладки:

Если вы работаете одновременно лишь с одним символом, можете изменить любое из его свойств и даже структуру, добавив или удалив компоненты. При выборе нескольких символов можно изменять только основные свойства символов в зависимости от их типа, как показано в следующей таблице:

Тип символа	Основные свойства
Полигон	Цвет Цвет контура Ширина контура
Линия	Цвет Ширина линии
Точка	Форма символа заливки, полигональный символ, который используется для заполнения формы. Также доступны вложенные свойства для этого слоя: Цвет Цвет контура Ширина контура Размер Угол Гало Выравнивание по углу, только в контексте 2D-карты Рекламный щит, только в контексте 3D Порядок поворота, только в контексте 3D
Сетка

Применение символов к векторным слоям

1. Выберите векторный слой на панели Содержание, щелкнув его название.

   На ленте появится контекстная вкладка Векторный слой.

2. Для Векторный слой вкладки Отображение в группе Оформление щелкните стрелку под Символы , чтобы выбрать, как отображать слой:

   Появится панель Символы, позволяющая дополнительно настроить способ классификации и обозначения слоя.

3. Щелкните символ на панели Символы, чтобы открыть панель Символы в режиме Формат символа и внести изменения.

   Чтобы изменить основные свойства более чем одного символа за раз, нажмите Shift+щелчок или Ctrl+щелчок, чтобы выбрать символы, затем щелкните правой кнопкой мыши и выберите Формат символов. Чтобы изменить все символы, щелкните Больше > Форматировать все символы.

4. В режиме форматирования символов на панели Символы либо выберите новый стиль на палитре символов, либо измените имеющиеся символы:

   Если щелкнуть символ в Галерее, он сразу же применится к выбранному классу или классам слоя.

5. Вы можете изменить текущий символ или символы на вкладке Символ в Свойствах.
   1. Предварительный просмотр выбранных символов доступен в нижней части панели Символы в режиме форматирования символов. С помощью стрелок сбоку от предварительного просмотра можно просмотреть ряд символов одновременно, если выбрано несколько символов. Чтобы узнать, как предварительно просмотреть символы, см. Просмотр текущего символа.
   2. Щелкните Применить, чтобы подтвердить изменения условных обозначений и перерисовать карту.
6. Нажмите кнопку Назад , чтобы вернуться к панели Символы.

Подсказка:

Также можно вернуться в режим форматирования символов на панели Символы, если щелкнуть символ на панели Содержание.

Применение условного символа легенды

Для одного символа, уникальных значений, градуированных цветов и градуированных символов можно дополнительно обозначить данные векторного слоя, изменив участок легенды любого линейного или полигонального векторного слоя. Образцы символов легенды изменяют форму предварительного просмотра символа, отображаемую на панелях Символы и Содержание, а также в легендах компоновки.

Чтобы изменить форму образца легенды слоя, выполните следующие действия:

1. Выберите векторный слой на панели Содержание, щелкнув его название.

   На ленте появится контекстная вкладка Векторный слой.

2. В группе вкладок Векторный слой на вкладке Оформление в группе Отображение щелкните кнопку Символы .
3. На панели Символы на вкладке Основные символы щелкните стрелку ниспадающего списка Обновить форму условного символа легенды рядом с символом.
4. Выберите форму условного символа легенды из меню.

   Линия	Горизонтальный Зигзаг Под углом Дуга Кривая Тропа Река
   Полигон	Прямоугольник Скругленный прямоугольник Окружность Эллипс Здание Граница Водоемы Природная область Квадратная область Шестиугольная область (плоская вершина) Шестиугольная область (заостренная вершина)

Связанные разделы

---

Отзыв по этому разделу?

Прошлое и будущее / Блог компании Wolfram Research / Хабр

Перевод поста Стивена Вольфрама (Stephen Wolfram) «Mathematical Notation: Past and Future (2000)».
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации

---

Содержание

Резюме
Введение
История
Компьютеры
Будущее
Примечания

—

Эмпирические законы для математических обозначений

—

Печатные обозначения против экранных

—

Письменные обозначения

—

Шрифты и символы

—

Поиск математических формул

—

Невизуальные обозначения

—

Доказательства

—

Отбор символов

—

Частотное распределение символов

—

Части речи в математической нотации

---

Стенограмма речи, представленной на секции «MathML и математика в сети» первой Международной Конференции MathML в 2000-м году.

---

Большинство математических обозначений существуют уже более пятисот лет. Я рассмотрю, как они разрабатывались, что было в античные и средневековые времена, какие обозначения вводили Лейбниц, Эйлер, Пеано и другие, как они получили распространение в 19 и 20 веках. Будет рассмотрен вопрос о схожести математических обозначений с тем, что объединяет обычные человеческие языки. Я расскажу об основных принципах, которые были обнаружены для обычных человеческих языков, какие из них применяются в математических обозначениях и какие нет.

Согласно историческим тенденциям, математическая нотация, как и естественный язык, могла бы оказаться невероятно сложной для понимания компьютером. Но за последние пять лет мы внедрили в Mathematica возможности к пониманию чего-то очень близкого к стандартной математической нотации. Я расскажу о ключевых идеях, которые сделали это возможным, а также о тех особенностях в математических обозначениях, которые мы попутно обнаружили.

Большие математические выражения — в отличии от фрагментов обычного текста — часто представляют собой результаты вычислений и создаются автоматически. Я расскажу об обработке подобных выражений и о том, что мы предприняли для того, чтобы сделать их более понятными для людей.

Традиционная математическая нотация представляет математические объекты, а не математические процессы. Я расскажу о попытках разработать нотацию для алгоритмов, об опыте реализации этого в APL, Mathematica, в программах для автоматических доказательств и других системах.

Обычный язык состоит их строк текста; математическая нотация часто также содержит двумерные структуры. Будет обсуждён вопрос о применении в математической нотации более общих структур и как они соотносятся с пределом познавательных возможностей людей.

Сфера приложения конкретного естественного языка обычно ограничивает сферу мышления тех, кто его использует. Я рассмотрю то, как традиционная математическая нотация ограничивает возможности математики, а также то, на что могут быть похожи обобщения математики.

Когда собиралась эта конференция, люди подумали, что было бы здорово пригласить кого-то для выступления с речью об основаниях и общих принципах математической нотации. И был очевидный кандидат —

Флориан Каджори

— автор классической книги под названием «

История математических обозначений

». Но после небольшого расследования оказалось, что есть техническая проблема в приглашении доктора Каджори — он умер как минимум лет семьдесят назад.

Так что мне придётся его заменять.

Полагаю, других вариантов особо-то и не было. Поскольку оказывается, что нет почти никого, кто жив на данный момент и кто занимался фундаментальными исследованиями математической нотации.

В прошлом математической нотацией занимались обычно в контексте систематизации математики. Так, Лейбниц и некоторые другие люди интересовались подобными вещами в середине 17 века. Бэббидж написал тяжеловесный труд по этой теме в 1821 году. И на рубеже 19 и 20 веков, в период серьёзного развития абстрактной алгебры и математической логики, происходит очередной всплеск интереса и деятельности в этой теме. Но после этого не было почти ничего.

Однако не особо удивительно, что я стал интересоваться подобными вещами. Потому что с Mathematica одной из моих главных целей было сделать ещё один большой шаг в области систематизации математики. А более общей моей целью в отношении Mathematica было распространить вычислительную мощь на все виды технической и математической работы. Эта задача имеет две части: то, как вычисления происходят внутри, и то, как люди направляют эти вычисления для получения того, что они хотят.

Одно из самых больших достижений Mathematica, о котором, вероятно, большинство из вас знает, заключается в сочетании высокой общности вычислений изнутри и сохранении практичности, основанной на преобразованиях символьных выражений, где символьные выражения могут представлять данные, графику, документы, формулы — да что угодно.

Однако недостаточно просто проводить вычисления. Необходимо так же, чтобы люди каким-то образом сообщали Mathematica о том, какие вычисления они хотят произвести. И основной способ дать людям взаимодействовать с чем-то столь сложным — использовать что-то вроде языка.

Обычно языки появляются в ходе некоторого поэтапного исторического процесса. Но компьютерные языки в историческом плане сильно отличаются. Многие были созданы практически полностью разом, зачастую одним человеком.

Так что включает в себя эта работа?

Ну, вот в чём заключалась для меня эта работа в отношении Mathematica: я попробовал представить, какие вообще вычисления люди будут производить, какие фрагменты в этой вычислительной работе повторяются снова и снова. А затем, собственно, я дал имена этим фрагментам и внедрил в качестве встроенных функций в Mathematica.

В основном мы отталкивались от английского языка, так как имена этих фрагментов основаны на простых английских словах. То есть это значит, что человек, который просто знает английский, уже сможет кое-что понять из написанного в Mathematica.

Однако, разумеется, язык Mathematica — не английский. Это скорее сильно адаптированный фрагмент английского языка, оптимизированный для передачи информации о вычислениях в Mathematica.

Можно было бы думать, что, пожалуй, было бы неплохо объясняться с Mathematica на обычном английском языке. В конце концов, мы уже знаем английский язык, так что нам было бы необязательно изучать что-то новое, чтобы объясняться с Mathematica.

Однако я считаю, что есть весьма весомые причины того, почему лучше думать на языке Mathematica, чем на английском, когда мы размышляем о разного рода вычислениях, которые производит Mathematica.

Однако мы так же знаем, заставить компьютер полностью понимать естественный язык — задача крайне сложная.

Хорошо, так что насчёт математической нотации?

Большинство людей, которые работают в Mathematica, знакомы по крайней мере с некоторыми математическими обозначениями, так что, казалось бы, было бы весьма удобно объясняться с Mathematica в рамках привычной математической нотации.

Но можно было бы подумать, что это не будет работать. Можно было бы подумать, что ситуация выльется в нечто, напоминающее ситуацию с естественными языками.

Однако есть один удивительный факт — он весьма удивил меня. В отличие от естественных человеческих языков, для обычной математической нотации можно сделать очень хорошее приближение, которое компьютер сможет понимать. Это одна из самых серьёзных вещей, которую мы разработали для третьей версии Mathematica в 1997 году [текущая версия Wolfram Mathematica — 10.4.1 — вышла в апреле 2016 г. — прим. ред.]. И как минимум некоторая часть того, что у нас получилось, вошла в спецификацию MathML.

Сегодня я хочу поговорить о некоторых общих принципах в математической нотации, которые мне довелось обнаружить, и то, что это означает в контексте сегодняшних дней и будущего.

В действительности, это не математическая проблема. Это куда ближе к лингвистике. Речь не о том, какой бы могла быть математическая нотация, а о том, какова используемая математическая нотация в действительности — как она развивалась в ходе истории и как связана с ограничениями человеческого познания.

Я думаю, математическая нотация — весьма интересное поле исследования для лингвистики.

Как можно было заметить, лингвистика в основном изучала разговорные языки. Даже пунктуация осталась практически без внимания. И, насколько мне известно, никаких серьёзных исследований математической нотации с точки зрения лингвистики никогда не проводилось.

Обычно в лингвистике выделяют несколько направлений. В одном занимаются вопросами исторических изменений в языках. В другом изучается то, как влияет изучение языка на отдельных людей. В третьем создаются эмпирические модели каких-то языковых структур.

Давайте сперва поговорим об истории.

Откуда произошли все те математические обозначения, которые мы в настоящее время используем?

Это тесно связано с историей самой математики, так что нам придётся коснуться немного этого вопроса. Часто можно услышать мнение, что сегодняшняя математика есть единственная мыслимая её реализация. То, какими бы могли быть произвольные абстрактные построения.

И за последние девять лет, что я занимался одним большим научным проектом, я ясно понял, что такой взгляд на математику не является верным. Математика в том виде, в котором она используется — это учение не о произвольных абстрактных системах. Это учение о конкретной абстрактной системе, которая исторически возникла в математике. И если заглянуть в прошлое, то можно увидеть, что есть три основные направления, из которых появилась математика в том виде, в котором мы сейчас её знаем — это арифметика, геометрия и логика.

Все эти традиции довольно стары. Арифметика берёт своё начало со времён древнего Вавилона. Возможно, и геометрия тоже приходит из тех времён, но точно уже была известна в древнем Египте. Логика приходит из древней Греции.

И мы можем наблюдать, что развитие математической нотации — языка математики — сильно связано с этими направлениями, особенно с арифметикой и логикой.

Следует понимать, что все три направления появлялись в различных сферах человеческого бытия, и это сильно повлияло на используемые в них обозначения.

Арифметика, вероятно, возникла из нужд торговли, для таких вещей, как, к примеру, счёт денег, а затем арифметику подхватили астрология и астрономия. Геометрия, по всей видимости, возникла из землемерческих и подобных задач. А логика, как известно, родилась из попытки систематизировать аргументы, приведённые на естественном языке.

Примечательно, кстати, что другая, очень старая область знаний, о которой я упомяну позднее — грамматика — по сути никогда не интегрировалась с математикой, по крайней мере до совсем недавнего времени.

Итак, давайте поговорим о ранних традициях в обозначениях в математике.

Во-первых, есть арифметика. И самая базовая вещь для арифметики — числа. Так какие обозначения использовались для чисел?

Что ж, первое представление чисел, о котором доподлинно известно — высечки на костях, сделанные 25 тысяч лет назад. Это была унарная система: чтобы представить число 7, нужно было сделать 7 высечек, ну и так далее.

Конечно, мы не можем точно знать, что именно это представление чисел было самым первым. Я имею ввиду, что мы могли и не найти свидетельств каких-то других, более ранних представлений чисел. Однако, если кто-то в те времена изобрёл какое-то необычное представление для чисел, и разместил их, к примеру, в наскальной живописи, то мы можем никогда и не узнать, что это было представление чисел — мы можем воспринимать это просто как какие-то фрагменты украшений.

Таким образом, числа можно представлять в унарной форме. И такое впечатление, что эта идея возрождалась множество раз и в различных частях света.

Но если посмотреть на то, что произошло помимо этого, то можно обнаружить довольно много различий. Это немного напоминает то, как различные виды конструкций для предложений, глаголов и прочее реализованы в различных естественных языках.

И, фактически, один из самых важных вопросов относительно чисел, который, как я полагаю, будет всплывать ещё много раз — насколько сильным должно быть соответствие между обычным естественным языком и языком математики?

Или вот вопрос: он связан с позиционной нотацией и повторным использованием цифр.

Как можно заметить, в естественных языках обычно есть такие слова, как «десять«, «сто«, «тысяча«, «миллион» и так далее. Однако в математике мы можем представить десять как «один нуль» (10), сто как «один нуль нуль» (100), тысячу как «один нуль нуль нуль» (1000) и так далее. Мы можем повторно использовать эту одну цифру и получать что-то новое, в зависимости от того, где в числе она будет появляться.

Что ж, это сложная идея, и людям потребовались тысячи лет, чтобы её действительно принять и осознать. А их неспособность принять её ранее имела большие последствия в используемых ими обозначениях как для чисел, так и для других вещей.

Как это часто бывает в истории, верные идеи появляются очень рано и долгое время остаются в забвении. Более пяти тысяч лет назад вавилоняне, и возможно даже до них ещё и шумеры разработали идею о позиционном представлении чисел. Их система счисления была шестидесятеричная, а не десятичная, как у нас. От них мы унаследовали представление секунд, минут и часов в существующей ныне форме. Но у них была идея использования одних и тех же цифр для обозначения множителей различных степеней шестидесяти.

Вот пример их обозначений.

Из этой картинки можно понять, почему археология столь трудна. Это очень маленький кусок обожжённой глины. Было найдено около полумиллиона подобных вавилонских табличек. И примерно одна из тысячи — то есть всего около 400 — содержат какие-то математические записи. Что, кстати, выше отношения математических текстов к обычным в современном интернете. Вообще, пока MathML не получил достаточного распространения, это является достаточно сложным вопросом.

Но, в любом случае, маленькие обозначения на этой табличке выглядят слегка похожими на отпечатки лапок крошечных птиц. Но почти 50 лет назад в конце концов исследователи определили, что эта клинописная табличка времён Хаммурапи — около 1750 года до н.э. — фактически является таблицей того, что мы сейчас называем пифагорейскими тройками.

Что ж, эти вавилонские знания были утеряны для человечества почти на 3000 лет. И вместо этого использовались схемы, основанные на естественных языках, с отдельными символами для десяти, ста и так далее.

Так, к примеру, у египтян для обозначения тысячи использовался символ цветка лотоса, для сотни тысяч — птица, ну и так далее. Каждая степень десяти для её обозначения имела отдельный символ.

А затем появилась другая очень важная идея, до которой не додумались ни вавилоняне, ни египтяне. Она заключалась в обозначении чисел цифрами — то есть не обозначать число семь семью единицами чего-то, а лишь одним символом.

Однако, у греков, возможно, как и у финикийцев ранее, эта идея уже была. Ну, на самом деле, она была несколько отличной. Она заключалась в том, чтобы обозначать последовательность чисел через последовательность букв в их алфавите. То есть альфе соответствовала единица, бете — двойка и так далее.

Вот как выглядит список чисел в греческом обозначении [вы можете скачать Wolfram Language Package, позволяющий представить числа в различных древних нотациях здесь — прим. ред.].

(Думаю, именно так сисадмины из Академии Платона адаптировали бы свою версию Mathematica; их воображаемую -600-ю (или около того) версию Mathematica.)

С этой системой счисления сопряжено множество проблем. Например, есть серьёзная проблема управления версиями: даже если вы решаете удалить какие-то буквы из своего алфавита, то вы должны оставить их в числах, иначе все ваши ранее записанные числа будут некорректными.

То есть это значит, что есть различные устаревшие греческие буквы, оставшиеся в системе счисления — как коппа для обозначения числа 90 и сампи для обозначения числа 900. Однако я включил их в набор символов для Mathematica, потому здесь прекрасно работает греческая форма записи чисел.

Спустя некоторое время римляне разработали свою форму записи чисел, с которой мы хорошо знакомы.

Пускай сейчас и не совсем ясно, что их цифры изначально задумывались как буквы, однако об этом следует помнить.

Итак, давайте попробуем римскую форму записи чисел.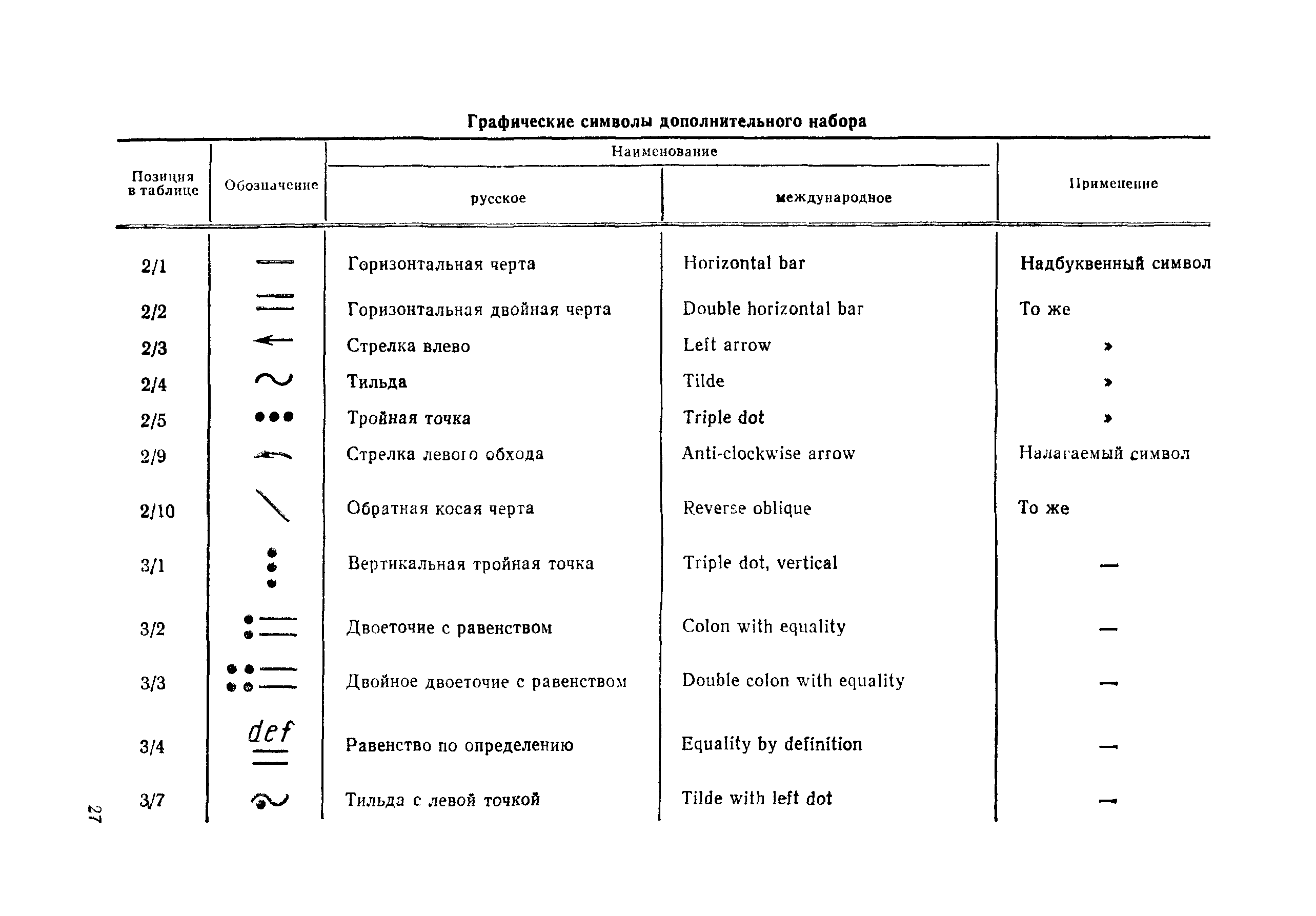

Это тоже довольно неудобный способ записи, особенно для больших чисел.

Тут есть несколько интересных моментов. К примеру, длина представляемого числа рекурсивно возрастает с размером числа.

И в целом, подобное представление для больших чисел полно неприятных моментов. К примеру, когда Архимед писал свою работу о количестве песчинок, объём которых эквивалентен объёму вселенной (Архимед оценил их количество в 10⁵¹, однако, полагаю, правильный ответ будет около 10⁹⁰), то он использовал обычные слова вместо обозначений, чтобы описать столь большое число.

Но на самом деле есть более серьёзная понятийная проблема с идеей о представлении цифр как букв: становится трудно придумать представление символьных переменных — каких-то символьных объектов, за которыми стоят числа. Потому что любую букву, которую можно было бы использовать для этого символьного объекта, можно будет спутать с цифрой или фрагментом числа.

Общая идея о символьном обозначении каких-то объектов через буквы известна довольно давно. Евклид, по сути, использовал эту идею в своих трудах по геометрии.

К сожалению, не сохранилось оригиналов работ Евклида. Однако имеются на несколько сот лет более молодые версии его работ. Вот одна, написанная на греческом языке.

И на этих геометрических фигурах можно увидеть точки, которые имеют символьное представление в виде греческих букв. И в описании теорем есть множество моментов, в которых точки, линии и углы имеют символьное представление в виде букв. Так что идея о символьном представлении каких-то объектов в виде букв берёт своё начало как минимум от Евклида.

Однако эта идея могла появиться и раньше. Если бы я умел читать на вавилонском, я бы, вероятно, смог бы сказать вам точно. Вот вавилонская табличка, в которой представляется квадратный корень из двух, и которая использует вавилонские буквы для обозначений.

Полагаю, обожжённая глина более долговечна, чем папирус, и получается, что мы знаем о том, что писали вавилоняне больше, чем о том, что писали люди вроде Евклида.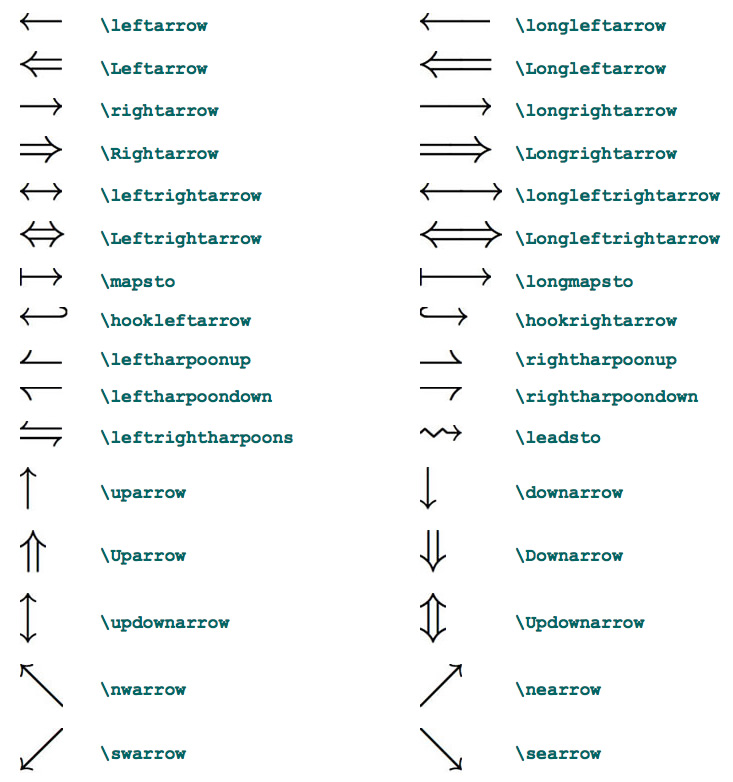

Вообще, эта неспособность увидеть возможность вводить имена для числовых переменных есть интересный случай, когда языки или обозначения ограничивают наше мышление. Это то, что несомненно обсуждается в обычной лингвистике. В наиболее распространённой формулировке эта идея звучит как гипотеза Сепира-Уорфа (гипотеза лингвистической относительности).

Разумеется, для тех из нас, кто потратил некоторую часть своей жизни на разработку компьютерных языков, эта идея представляется очень важной. То есть я точно знаю, что если я буду думать на языке Mathematica, то многие концепции будут достаточно просты для моего понимания, и они будут совсем не такими простыми, если я буду думать на каком-то другом языке.

Но, в любом случае, без переменных всё было бы гораздо сложнее. Например, как вы представите многочлен?

Ну, Диофант — тот самый, что придумал диофантовы уравнения — сталкивался с проблемой представления многочленов в середине 2 века н.э. В итоге он пришёл к использованию определённых основанных на буквах имён для квадратов, кубов и прочего.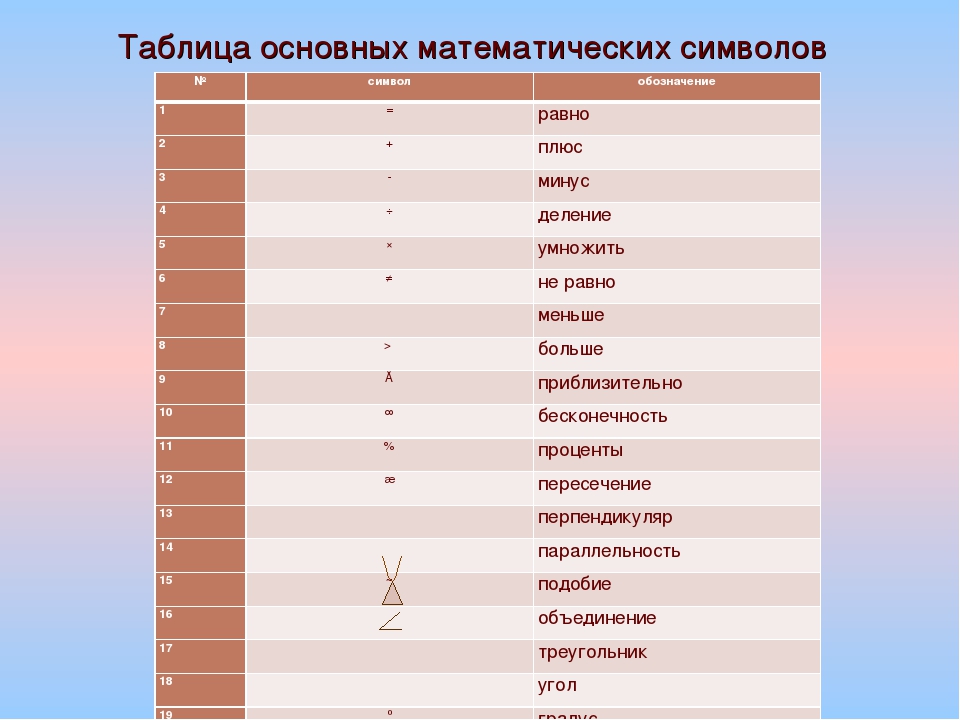 Вот как это работало.

По крайней мере сейчас нам показалось бы чрезвычайно трудным понять обозначения Диофанта для полиномов. Это пример не очень хороших обозначений. Полагаю, главная причина, помимо ограниченной расширяемости, состоит в том, что эти обозначения делают математические связи между полиномами неочевидными и не выделяют наиболее интересные нам моменты.

Есть и другие схемы задания полиномов без переменных, как, например, китайская схема, которая включала создание двухмерного массива коэффициентов.

Проблема здесь, опять-таки, в расширяемости. И эта проблема с основанными на графике обозначениями всплывает снова и снова: лист бумаги, папирус или что бы то ни было — они все ограничены двумя измерениями.

Хорошо, так что насчёт буквенного обозначения переменных?

Полагаю, что они могли бы появиться лишь после появления чего-то похожего на нашу современную нотацию. И она до определённого времени не появлялась. Были какие-то намёки в индо-арабских обозначениях в середине первого тысячелетия, однако установилось всё лишь к его концу. А на запад эта идея пришла лишь с работой Фибоначчи о вычислениях в 13 веке.

Фибоначчи, разумеется, был тем самым, кто говорил о числах Фибоначчи применительно к задаче о кроликах, однако в действительности эти числа известны были уже более тысячи лет, и служили они для описания форм индийской поэзии. И я всегда находил случай с числами Фибоначчи удивительным и отрезвляющим эпизодом в истории математики: возникнув на заре западной математики, столь привычные и фундаментальные, они начали становиться популярными лишь в 80-е.

В любом случае, также интересно заметить, что идея разбивки цифр в группы по три, чтобы сделать большие числа более читаемыми, имеется уже в книге Фибоначчи 1202 года, хотя я думаю, что он говорил об использовании скобок над числами, а не о разделяющих запятых.

После Фибоначчи наше современное представление для чисел постепенно становится всё популярнее, и ко времени начала книгопечатания в 15 веке оно уже было универсальным, хотя ещё и оставались несколько чудных моментов.

Но алгебраических переменных в полном их смысле тогда ещё не было. Они появились лишь после Виета в конце 16 века и обрели популярность лишь в 17 веке. То есть у Коперника и его современников их ещё не было. Как в основном и у Кеплера. Эти учёные для описания каких-то математических концепций использовали обычный текст, иногда структурированный как у Евклида.

Кстати, даже несмотря на то, что математическая нотация в те времена была не очень хорошо проработана, системы символьных обозначений в алхимии, астрологии и музыке были довольно развиты. Так, к примеру, Кеплер в начале 17 века использовал нечто, похожее на современную музыкальную нотацию, объясняя свою «музыку сфер» для отношений планетарных орбит.

Со времён Виета буквенные обозначения для переменных стали привычным делом. Обычно, кстати, он использовал гласные для неизвестных и согласные — для известных.

Вот как Виет записывал многочлены в форме, которую он называл «zetetics«, а сейчас мы бы это назвали просто символьной алгеброй:

Можно увидеть, что он использует слова для обозначения операций, в основном так, чтобы их нельзя было спутать с переменными.

Так как раньше представляли операции, в каком виде?

Идея о том, что операции есть нечто, что можно в какой-то форме представить, добиралась до умов людей довольно долго. Вавилоняне обычно не использовали символы для операций — для сложения они просто записывали слагаемые друг за другом. И в целом они были предрасположены записывать всё в виде таблиц, так что им не требовалось как-то обозначать операции.

У египтян были некоторые обозначения для операций: для сложения они использовали пару идущих вперёд ног, а для вычитания — идущих назад.

А современный знак +, который, вероятно, является сокращением от «et» на латыни (означает «и»), появился лишь в конце 15 века.

А вот кое-что из 1579 года, что выглядит весьма современным, написанное в основном на английском, пока не начнёшь понимать, что те забавные загогулины — это не иксы, а специальные небуквенные символы, которые представляют различные степени для переменных.

В первой половине 17 века произошла своего рода революция в математической нотации, после которой она практически обрела свой современный вид. Было создано современное обозначение квадратного корня, который ранее обозначался как Rx — это обозначение сейчас используется в медицинских рецептах. И в основном алгебраическая нотация приобрела свой современный вид.

Уильям Отред был одним из тех людей, кто серьёзно занимался этим вопросом. Изобретение логарифмической линейки — одна из вещей, которая сделала его известным. На самом деле о нём практически ничего неизвестно. Он не был крупным математиком, однако сделал много полезного в области преподавания, с такими людьми, как Кристофер Рен и его учениками. Странно, что я ничего не слышал о нём в школе, особенно если учесть, что мы учились в одной и той же школе, только он на 400 лет ранее. Однако изобретение логарифмической линейки было недостаточным для того, чтобы увековечить своё имя в истории математики.

Но, в любом случае, он серьёзно занимался нотацией. Он придумал обозначать умножение крестиком, и он продвинул идею о представлении алгебры посредством обозначений вместо слов — так, как это делал Виет. И, фактически, он изобрёл довольно много других обозначений, подобно тильде для таких предикатов, как IntegerQ.

После Отреда и его сотоварищей эти обозначения быстро установились. Были и альтернативные обозначения, как изображения убывающей и растущей лун для обозначения арифметических операций — прекрасный пример плохого и нерасширяемого дизайна. Однако в основном использовались современные обозначения.

Вот пример.

Это фрагмент рукописи Ньютона Principia, из которой ясно, что он в основном использовал современные алгебраические обозначения. Думаю, именно Ньютон придумал использовать отрицательные степени вместо дробей для обратных величин и прочего. Principia содержит весьма мало обозначений, за исключением этих алгебраических вещей и представления разного материала в стиле Евклида. И в действительности Ньютон не особо интересовался обозначениями. Он даже хотел использовать точечные обозначения для своих флюксий.

Чего не скажешь о Лейбнице. Лейбниц много внимания уделял вопросам нотации. В действительности, он считал, что правильные обозначения есть ключ ко многим человеческим вопросам. Он был своего рода дипломат-аналитик, курсирующий между различными странами, со всеми их различными языками, и т.д. У него была идея, что если создать некий универсальный логический язык, то тогда все люди смогли бы понимать друг друга и имели бы возможность объяснить всё что угодно.

Были и другие люди, которые размышляли о подобном, преимущественно с позиции обычных естественных языков и логики. Один из примеров — довольно специфичный персонаж по имени Раймонд Лул, живший в 14 веке, который заявлял, что изобрёл некие логические колёса, дающие ответы на все вопросы мира.

Но так или иначе, Лейбниц разработал те вещи, которые были интересны и с позиций математики. То, что он хотел сделать, должно было так или иначе объединить все виды обозначений в математике в некоторый точный естественный язык с подобным математике способом описания и решения различных проблем, или даже больше — объединить ещё и все используемые естественные языки.

Ну, как и многие другие свои проекты, Лейбниц так и не воплотил это в жизнь. Однако он занимался самыми разными направлениями математики и серьёзно относился к разработке обозначений для них. Наиболее известные его обозначения были введены им в 1675 году. Для обозначения интегралов он использовал «omn.«, возможно, как сокращение от omnium. Но в пятницу 29 октября 1675 года он написал следующее.

На этом фрагменте бумаги можно увидеть знак интеграла. Он задумывал его как вытянутую S. Несомненно, это и есть современное обозначение интеграла. Ну, между обозначениями интегралов тогда и сейчас почти нет никакой разницы.

Затем в четверг 11 ноября того же года он обозначил дифференциал как «d«. На самом деле, Лейбниц считал это обозначение не самым лучшим и планировал придумать ему какую-нибудь замену. Но, как мы все знаем, этого не произошло.

Что ж, Лейбниц вёл переписку касательно обозначений с самыми разными людьми. Он видел себя кем-то вроде председателя комитета стандартов математических обозначений — так бы мы сказали сейчас. Он считал, что обозначения должны быть максимально краткими. К примеру, Лейбниц говорил: «Зачем использовать две точки для обозначения деления, когда можно использовать лишь одну?«.

Некоторые из продвигаемых им идей так и не получили распространения. К примеру, используя буквы для обозначения переменных, он использовал астрономические знаки для обозначения выражений. Довольно интересная идея, на самом деле.

Так он обозначал функции.

Помимо этих моментов и некоторых исключений наподобие символа пересечения квадратов, который Лейбниц использовал для обозначения равенства, его обозначения практически неизменными дошли до наших дней.

В 18 веке Эйлер активно пользовался обозначениями. Однако, по сути, он следовал по пути Лейбница. Полагаю, он был первым, кто всерьёз начал использовать греческие буквы наравне с латинскими для обозначения переменных.

Есть и некоторые другие обозначения, которые появились вскоре после Лейбница. Следующий пример из книги, вышедшей через несколько лет после смерти Ньютона. Это учебник алгебры, и он содержит весьма традиционные алгебраические обозначения, уже в печатном виде.

А вот книга Лопиталя, напечатанная примерно в то же время, в которой уже практически современная алгебраическая нотация.

И, наконец, вот пример от Эйлера, содержащий весьма современные обозначения для интегралов и прочего.

Эйлер — популяризировал современное обозначение для числа пи, которое первоначально было предложено Уильямом Джонсом, который рассматривал его как сокращение от слова периметр.

Предложенная Лейбницем и сотоварищами нотация довольно долго оставалась неизменной. Происходили небольшие изменения, как, к примеру квадрат x x получил написание x². Однако практически ничего нового не появилось.

Однако в конце 19 века наблюдается новый всплеск интереса к математической нотации, сопряжённый с развитием математической логики. Были некоторые нововведения, сделанные физиками, такими как Максвелл и Гиббс, в основном для векторов и векторного анализа, как следствие развития абстрактной алгебры. Однако наиболее значимые изменения были сделаны людьми, начиная с Фреге и приблизительно с 1879 года, которые занимались математической логикой.

Эти люди в своих устремлениях были близки к Лейбницу. Они хотели разработать нотацию, которая представляла бы не только математические формулы, но и математические выводы и доказательства. В середине 19 века Буль показал, что основы логики высказываний можно представлять в терминах математики. Однако Фреге и его единомышленники хотели пойти дальше и представить так как логику высказываний, так и любые математические суждения в соответствующих математических терминах и обозначениях.

Фреге решил, что для решения этой задачи потребуются графические обозначения. Вот фрагмент его так называемой «концептуальной нотации«.

К сожалению, в ней трудно разобраться. И в действительности, если посмотреть на историю обозначений в целом, то часто можно встретить попытки изобретения графических обозначений, которые оказывались трудными для понимания. Но в любом случае, обозначения Фреге уж точно не стали популярными.

Потом был Пеано, самый главный энтузиаст в области математической нотации. Он делал ставку на линейное представление обозначений. Вот пример:

Вообще говоря, в 80-х годах 19 века Пеано разработал то, что очень близко к обозначениям, которые используются в большинстве современных теоретико-множественных концепций.

Однако, как и Лейбниц, Пеано не желал останавливаться лишь на универсальной нотации для математики. Он хотел разработать универсальный язык для всего. Эта идея реализовалась у него в то, что он назвал интерлингва — язык на основе упрощённой латыни. Затем он написал нечто вроде краткого изложения математики, назвав это Formulario Mathematico, которое было основано на его обозначениях для формул, и труд этот был написал на этой производной от латыни — на интерлингве.

Интерлингва, подобно эсперанто, который появился примерно в это же время, так и не получил широкого распространения. Однако этого нельзя сказать об обозначениях Пеано. Сперва о них никто ничего толком и не слышал. Но затем Уайтхед и Рассел написали свой труд Principia Mathematica, в котором использовались обозначения Пеано.

Думаю, Уайтхед и Рассел выиграли бы приз в номинации «самая насыщенная математическими обозначениями работа, которая когда-либо была сделана без помощи вычислительных устройств«. Вот пример типичной страницы из Principia Mathematica.

У них были все мыслимые виды обозначений. Частая история, когда авторы впереди своих издателей: Рассел сам разрабатывал шрифты для многих используемых им обозначений.

И, разумеется, тогда речь шла не о шрифтах TrueType или о Type 1, а о самых настоящих кусках свинца. Я о том, что Рассела можно было встретить с тележкой, полной свинцовых оттисков, катящему её в издательство Кембриджского университета для обеспечения корректной вёрстки его книг.

Но, несмотря на все эти усилия, результаты были довольно гротескными и малопонятными.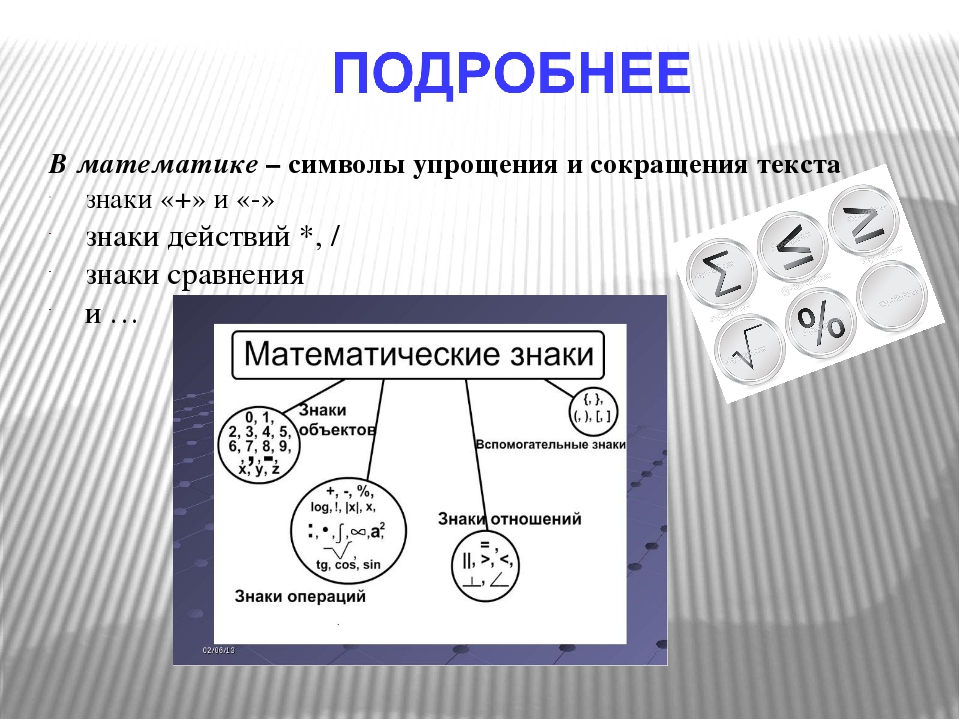 Я думаю, это довольно ясно, что Рассел и Уайтхед зашли слишком далеко со своими обозначениями.

И хотя область математической логики немного прояснилась в результате деятельности Рассела и Уайтхеда, она всё ещё остаётся наименее стандартизированной и содержащей самую сложную нотацию.

Но что насчёт более распространённых составляющих математики?

Какое-то время в начале 20 века то, что было сделано в математической логике, ещё не произвело никакого эффекта. Однако ситуация резко начала меняться с движением Бурбаки, которое начало разрастаться во Франции в примерное сороковые года.

Бурбаки придавали особое значение гораздо более абстрактному, логико-ориентированному подходу к математике. В частности, они акцентировали внимание на использовании обозначений там, где это только возможно, любым способом сводя использование потенциально неточного текста к минимуму.

Где-то с сороковых работы в области чистой математики претерпели серьёзные изменения, что можно заметить в соответствующих журналах, в работах международного математического сообщества и прочих источниках подобного рода. Изменения заключались в переходе от работ, полных текста и лишь с основными алгебраическими и вычислительными выкладками к работам, насыщенными обозначениями.

Конечно, эта тенденция коснулась не всех областей математики. Это в некотором роде то, чем занимаются в лингвистике обычных естественных языков. По устаревшим используемым математическим обозначениям можно заметить, как различные области, их использующие, отстают от основной магистрали математического развития. Так, к примеру, можно сказать, что физика осталась где-то в конце 19 века, используя уже устаревшую математическую нотацию тех времён.

Есть один момент, который постоянно проявляется в этой области — нотация, как и обычные языки, сильно разделяет людей. Я имею в виду, что между теми, кто понимает конкретные обозначения, и теми, кто не понимает, имеется большой барьер. Это кажется довольно мистическим, напоминая ситуацию с алхимиками и оккультистами — математическая нотация полна знаков и символов, которые люди в обычной жизни не используют, и большинство людей их не понимают.

На самом деле, довольно любопытно, что с недавних пор в рекламе появился тренд на использование математических обозначений. Думаю, по какой-то причине математическая нотация стала чем-то вроде шика. Вот один актуальный пример рекламы.

Отношение к математическим обозначениям, к примеру, в школьном образовании, часто напоминает мне отношение к символам секретных сообществ и тому подобному.

Что ж, это был краткий конспект некоторых наиболее важных эпизодов истории математической нотации.

В ходе исторических процессов некоторые обозначения перестали использоваться. Помимо некоторых областей, таких как математическая логика, она стала весьма стандартизированной. Разница в используемых разными людьми обозначениях минимальна. Как и в ситуации с любым обычным языком, математические записи практически всегда выглядят одинаково.

Вот вопрос:

можно ли сделать так, чтобы компьютеры понимали эти обозначения?

Это зависит от того, насколько они систематизированы и как много смысла можно извлечь из некоторого заданного фрагмента математической записи.

Ну, надеюсь, мне удалось донести мысль о том, что нотация развивалась в результате непродуманных случайных исторических процессов. Было несколько людей, таких как Лейбниц и Пеано, которые пытались подойти к этому вопросу более системно. Но в основном обозначения появлялись по ходу решения каких-то конкретных задач — подобно тому, как это происходит в обычных разговорных языках.

И одна из вещей, которая меня удивила, заключается в том, что по сути никогда не проводилось интроспективного изучения структуры математической нотации.

Грамматика обычных разговорных языков развивалась веками. Без сомнения, многие римские и греческие философы и ораторы уделяли ей много внимания. И, по сути, уже примерно в 500 года до н. э. Панини удивительно подробно и ясно расписал грамматику для санскрита. Фактически, грамматика Панини была удивительно похожа по структуре на спецификацию правил создания компьютерных языков в форме Бэкуса-Наура, которая используется в настоящее время.

И были грамматики не только для языков — в последнее столетие появилось бесконечное количество научных работ по правильному использованию языка и тому подобному.

Но, несмотря на всю эту активность в отношении обычных языков, по сути, абсолютно ничего не было сделано для языка математики и математической нотации. Это действительно довольно странно.

Были даже математики, которые работали над грамматиками обычных языков. Ранним примером являлся Джон Уоллис, который придумал формулу произведения Уоллиса для числа пи, и вот он писал работы по грамматике английского языка в 1658 году. Уоллис был тем самым человеком, который начал всю эту суматоху с правильным использованием «will» или «shall«.

В начале 20 века в математической логике говорили о разных слоях правильно сформированного математического выражения: переменные внутри функций внутри предикатов внутри функций внутри соединительных слов внутри кванторов. Но не о том, что же это всё значило для обозначений выражений.

Некоторая определённость появилась в 50-е годы 20 века, когда Хомский и Бакус, независимо разработали идею контекстно-свободных языков. Идея пришла походу работы над правилами подстановки в математической логике, в основном благодаря Эмилю Посту в 20-х годах 20 века. Но, любопытно, что и у Хомского, и у Бакуса возникла одна и та же идея именно в 1950-е.

Бакус применил её к компьютерным языкам: сперва к Fortran, затем к ALGOL. И он заметил, что алгебраические выражения могут быть представлены в контекстно-свободной грамматике.

Хомский применил эту идею к обычному человеческому языку. И он отмечал, что с некоторой степенью точности обычные человеческие языки так же могут быть представлены контекстно-свободными грамматиками.

Конечно, лингвисты включая Хомского, потратили годы на демонстрацию того, насколько всё же эта идея не соответствует действительности. Но вещь, которую я всегда отмечал, а с научной точки зрения считал самой важной, состоит в том, что в первом приближении это всё-таки истина — то, что обычные естественные языки контекстно-свободны.

Итак, Хомский изучал обычный язык, а Бакус изучал такие вещи, как ALGOL. Однако никто из них не рассматривал вопрос разработки более продвинутой математики, чем простой алгебраический язык. И, насколько я могу судить, практически никто с тех времён не занимался этим вопросом.

Но, если вы хотите посмотреть, сможете ли вы интерпретировать некоторые математические обозначения, вы должны знать, грамматику какого типа они используют.

Сейчас я должен сказать вам, что считал математическую нотацию чем-то слишком случайным для того, чтобы её мог корректно интерпретировать компьютер. В начале девяностых мы горели идеей предоставить возможность Mathematica работать с математической нотацией. И по ходу реализации этой идеи нам пришлось разобраться с тем, что происходит с математической нотацией.

Нил Сойффер потратил множество лет, работая над редактированием и интерпретацией математической нотации, и когда он присоединился к нам в 1991, он пытаться убедить меня, что с математической нотацией вполне можно работать — как с вводом, так и с выводом. 2+ArcSin[x+1]+c(x+1)+f[x+1]

Что оно означает? Чтобы это понять, нужно знать приоритеты операторов — какие действуют сильнее, а какие слабее в отношении операндов.

Я подозревал, что для этого нет какого-то серьёзного обоснования ни в каких статьях, посвящённых математике. И я решил исследовать это. Я прошёлся по самой разнообразной математической литературе, показывал разным людям какие-то случайные фрагменты математической нотации и спрашивал у них, как бы они их интерпретировали. И я обнаружил весьма любопытную вещь: была удивительная слаженность мнений людей в определении приоритетов операторов. Таким образом, можно утверждать: имеется определённая последовательность приоритетов математических операторов.

Можно с некоторой уверенностью сказать, что люди представляют именно эту последовательность приоритетов, когда смотрят на фрагменты математической нотации.

Обнаружив этот факт, я стал значительно более оптимистично оценивать возможность интерпретации вводимых математических обозначений. Один из способов, с помощью которого всегда можно это реализовать — использовать шаблоны. То есть достаточно просто иметь шаблон для интеграла и заполнять ячейки подынтегрального выражения, переменной и так далее. И когда шаблон вставляется в документ, то всё выглядит как надо, однако всё ещё содержится информация о том, что это за шаблон, и программа понимает, как это интерпретировать. И многие программы действительно так и работают.

Но в целом это крайне неудобно. Потому что если вы попытаетесь быстро вводить данные или редактировать, вы будете обнаруживать, что компьютер вам бикает (beeping) и не даёт делать те вещи, которые, очевидно, должны быть вам доступны для реализации.

Дать людям возможность ввода в свободной форме — значительно более сложная задача. Но это то, что мы хотим реализовать.

Итак, что это влечёт?

Прежде всего, математический синтаксис должен быть тщательно продуманным и однозначным. Очевидно, получить подобный синтаксис можно, если использовать обычный язык программирования с основанным на строках синтаксисом. Но тогда вы не получите знакомую математическую нотацию.

Вот ключевая проблема: традиционная математическая нотация содержит неоднозначности. По крайней мере, если вы захотите представить её в достаточно общем виде. Возьмём, к примеру, «i«. Что это — Sqrt[-1] или переменная «i«?

В обычном текстовом InputForm в Mathematica все подобные неоднозначности решены простым путём: все встроенные объекты Mathematica начинаются с заглавной буквы.

Но заглавная «I» не очень то и похожа на то, чем обозначается Sqrt[-1] в математических текстах. И что с этим делать? И вот ключевая идея: можно сделать другой символ, который вроде тоже прописная «i», однако это будет не обычная прописная «i», а квадратный корень из -1.

Можно было бы подумать: Ну, а почему бы просто не использовать две «i», которые бы выглядели одинаково, — прям как в математических текстах — однако из них будет особой? Ну, это бы точно сбивало с толку. Вы должны будете знать, какую именно «i» вы печатаете, а если вы её куда-то передвинете или сделаете что-то подобное, то получится неразбериха.

Итак, значит, должно быть два «i«. Как должна выглядеть особая версия этого символа?

У нас была идея — использовать двойное начертание для символа. Мы перепробовали самые разные графические представления. Но идея с двойным начертанием оказалась лучшей. В некотором роде она отвечает традиции в математике обозначать специфичные объекты двойным начертанием.

Так, к примеру, прописная R могла бы быть переменной в математических записях. А вот R с двойным начертанием — уже специфический объект, которым обозначают множество действительных чисел.

Таким образом, «i» с двойным начертанием есть специфичный объект, который мы называем ImaginaryI. Вот как это работает:

Идея с двойным начертанием решает множество проблем.

В том числе и самую большую — интегралы. Допустим, вы пытаетесь разработать синтаксис для интегралов. Один из ключевых вопросов — что может означать «d» в интеграле? Что, если это параметр в подынтегральном выражении? Или переменная? Получается ужасная путаница.

Всё становится очень просто, если использовать DifferentialD или «d» с двойным начертанием. И получается хорошо определённый синтаксис.

Можно проинтегрировать x в степени d, деленное на квадратный корень от x+1. Вот как это работает:

Оказывается, что требуется всего лишь несколько маленьких изменений в основании математического обозначения, чтобы сделать его однозначным. Это удивительно. И весьма здорово. Потому что вы можете просто ввести что-то, состоящее из математических обозначений, в свободной форме, и оно будет прекрасно понято системой. И это то, что мы реализовали в Mathematica 3.

Конечно, чтобы всё работало так, как надо, нужно разобраться с некоторыми нюансами. К примеру, иметь возможность вводить что бы то ни было эффективным и легко запоминающимся путём. , с помощью которой можно вводить явный верхний индекс. Та же идея для сочетания control — /, с помощью которого можно вводить «двухэтажную» дробь.

Наличие ясного набора принципов подобных этому важно для того, чтобы заставить всё вместе работать на практике. И оно работает. Вот как мог бы выглядеть ввод довольно сложного выражения:

Но мы можем брать фрагменты из этого результата и работать с ними.

И смысл в том, что это выражение полностью понятно для Mathematica, то есть оно может быть вычислено. Из этого следует, что результаты выполнения (Out) — объекты той же природы, что и входные данные (In), то есть их можно редактировать, использовать их части по отдельности, использовать их фрагменты в качестве входных данных и так далее.

Чтобы заставить всё это работать, нам пришлось обобщить обычные языки программирования и кое-что проанализировать. Прежде была внедрена возможность работать с целым «зоопарком» специальных символов в качестве операторов. Однако, вероятно, более важно то, что мы внедрили поддержку двумерных структур. Так, помимо префиксных операторов, имеется поддержка оверфиксных операторов и прочего.

Если вы посмотрите на это выражение, вы можете сказать, что оно не совсем похоже на традиционную математическую нотацию. Но оно очень близко. И оно несомненно содержит все особенности структуры и форм записи обычной математической нотации. И важная вещь заключается в том, что ни у кого, владеющим обычной математической нотацией, не возникнет трудностей в интерпретации этого выражения.

Конечно, есть некоторые косметические отличия от того, что можно было бы увидеть в обычном учебнике по математике. К примеру, как записываются тригонометрические функции, ну и тому подобное.

Однако я готов поспорить, что StandardForm в Mathematica лучше и яснее для представления этого выражения. И в книге, которую я писал много лет о научном проекте, которым я занимался, для представления чего бы то ни было я использовал только StandardForm.

Однако если нужно полное соответствие с обычными учебниками, то понадобится уже что-то другое. И вот другая важная идея, реализованная в Mathematica 3: разделить StandardForm и TraditionalForm.

Любое выражение я всегда могу сконвертировать в TraditionalForm.

И в действительности TraditionalForm всегда содержит достаточно информации, чтобы быть однозначно сконвертированным обратно в StandardForm.

Но TraditionalForm выглядит практически как обычные математические обозначения. Со всеми этими довольно странными вещами в традиционной математической нотации, как запись синус в квадрате x вместо синус x в квадрате и так далее.

Так что насчёт ввода TraditionalForm?

Вы могли заметить пунктир справа от ячейки [в других выводах ячейки были скрыты для упрощения картинок — прим. ред.]. Они означают, что есть какой-то опасный момент. Однако давайте попробуем кое-что отредактировать.

Мы прекрасно можем всё редактировать. Давайте посмотрим, что случится, если мы попытаемся это вычислить.

Вот, возникло предупреждение. В любом случае, всё равно продолжим.

Что ж, система поняла, что мы хотим.

Фактически, у нас есть несколько сотен эвристических правил интерпретации выражений в традиционной форме. И они работают весьма хорошо. Достаточно хорошо, чтобы пройти через большие объёмы устаревших математических обозначений, определённых, скажем, в TEX, и автоматически и однозначно сконвертировать их в осмысленные данные в Mathematica.

И эта возможность весьма вдохновляет. Потому что для того же устаревшего текста на естественном языке нет никакого способа сконвертировать его во что-то значимое. Однако в математике есть такая возможность.

Конечно, есть некоторые вещи, связанные с математикой, в основном на стороне выхода, с которыми существенно больше сложностей, чем с обычным текстом. Часть проблемы в том, что от математики часто ожидают автоматической работы. Нельзя автоматически сгенерировать много текста, который будет достаточно осмысленным. Однако в математике производятся вычисления, которые могут выдавать большие выражения.

Так что вам нужно придумывать, как разбивать выражение по строкам так, чтобы всё выглядело достаточно аккуратно, и в Mathematica мы хорошо поработали над этой задачей. И с ней связано несколько интересных вопросов, как, например, то, что во время редактирования выражения оптимальное разбиение на строки постоянно может меняться по ходу работы.

И это значит, что будут возникать такие противные моменты, как если вы печатаете, и вдруг курсор перескакивает назад. Что ж, эту проблему, полагаю, мы решили довольно изящным образом. Давайте рассмотрим пример.

Вы видели это? Была забавная анимация, которая появляется на мгновение, когда курсор должен передвинуться назад. Возможно, вы её заметили. Однако если бы вы печатали, вы бы, вероятно, и не заметили бы, что курсор передвинулся назад, хотя вы могли бы её и заметить, потому что эта анимация заставляет ваши глаза автоматически посмотреть на это место. С точки зрения физиологии, полагаю, это работает за счёт нервных импульсов, которые поступают не в зрительную кору, а прямо в мозговой ствол, который контролирует движения глаз. Итак, эта анимация заставляет вас подсознательно переместить свой взор в нужное место.

Таким образом, мы смогли найти способ интерпретировать стандартную математическую нотацию. Означает ли это, что теперь вся работа в Mathematica должна теперь проводиться в рамках традиционных математических обозначений? Должны ли мы ввести специальные символы для всех представленных операций в Mathematica? Таким образом можно получить весьма компактную нотацию. Но насколько это разумно? Будет ли это читаемо?

Пожалуй, ответом будет нет.

Думаю, тут сокрыт фундаментальный принцип: кто-то хочет всё представлять в обозначениях, и не использовать ничего другого.

А кому-то не нужны специальные обозначения. А кто-то пользуется в Mathematica FullForm. Однако с этой формой весьма утомительно работать. Возможно, именно поэтому синтаксис языков наподобие LISP кажется столь трудным — по сути это синтаксис FullForm в Mathematica.

Другая возможность заключается в том, что всему можно присвоить специальные обозначения. Получится что-то наподобие APL или каких-то фрагментов математической логики. Вот пример этого.

Довольно трудно читать.

Вот другой пример из оригинальной статьи Тьюринга, в которой содержатся обозначения для универсальной машины Тьюринга, опять-таки — пример не самой лучшей нотации.

Она тоже относительно нечитабельная.

Вопрос заключается в том, что же находится между двумя такими крайностями, как LISP и APL. Думаю, эта проблема очень близка к той, что возникала при использовании очень коротких имён для команд.

К примеру, Unix. Ранние версии Unix весьма здорово смотрелись, когда там было небольшое количество коротких для набора команд. Но система разрасталась. И через какое-то время было уже большое количество команд, состоящих из небольшого количества символов. И большинство простых смертных не смогли бы их запомнить. И всё стало выглядеть совершенно непонятным.

Та же ситуация, что и с математической или другой нотацией, если на то пошло. Люди могут работать лишь с небольшим количеством специальных форм и символов. Возможно, с несколькими десятками. Соизмеримым с длиной алфавита. Но не более. А если дать им больше, особенно все и сразу, в голове у них будет полная неразбериха.

Это следует немного конкретизировать. Вот, к примеру, множество различных операторов отношений.

Но большинство из них по сути состоят из небольшого количества элементов, так что с ними проблем быть не должно.

Конечно, принципиально люди могут выучить очень большое количество символов. Потому что в языках наподобие китайского или японского имеются тысячи иероглифов. Однако людям требуется несколько дополнительных лет для обучения чтению на этих языках в сравнении с теми, которые используют обычный алфавит.

Если говорить о символах, кстати, полагаю, что людям гораздо легче справится с какими-то новыми символами в качестве переменных, нежели в качестве операторов. И весьма занятно рассмотреть этот вопрос с точки зрения истории.

Один из наиболее любопытных моментов — во все времена и практически без исключения в качестве переменных использовались лишь латинские и греческие символы. Ну, Кантор ввёл алеф, взятый из иврита, для своих кардинальных чисел бесконечных множеств. И некоторые люди утверждают, что символ частной производной — русская д, хотя я думаю, что на самом деле это не так. Однако нет никаких других символов, которые были бы заимствованы из других языков и получили бы распространение.

Кстати, наверняка вам известно, что в английском языке буква «e» — самая популярная, затем идёт «t«, ну и так далее. И мне стало любопытно, каково распределение по частоте использования букв в математике. Потому я исследовал сайт MathWorld, в котором содержится большое количество математической информации — более 13 500 записей, и посмотрел, каково распределение для различных букв [к сожалению, эту картинку, сделанную Стивеном, не удалось осовременить — прим. ред.].

Можно увидеть, что «e» — самая популярная. И весьма странно, что «a» занимает второе место. Это очень необычно. Можно увидеть, что строчная π — наиболее популярная, за которой идут θ, α, φ, μ, β и так далее. А среди прописных самые популярные — Γ и Δ.

Хорошо. Я немного рассказал об обозначениях, которые в принципе можно использовать в математике. Так какая нотация лучше всего подходит для использования?

Большинство людей, использующих математическую нотацию, наверняка задавались этим вопросом. Однако для математики нет никакого аналога, подобного «Современному использованию английского языка» Фаулера для английского языка. Была небольшая книжка под названием Математика в печати, изданная AMS, однако она в основном о типографских приёмах.

В результате мы не имеем хорошо расписанных принципов, аналогичным вещам наподобие инфинитивов с отдельными частицами в английском языке.

Если вы используете StandardForm в Mathematica, вам это больше не потребуется. Потому что всё, что вы введёте, будет однозначно интерпретировано. Однако для TraditionalForm следует придерживаться некоторых принципов. К примеру, не писать , потому что не совсем ясно, что это означает.

Чтобы закончить, позвольте мне рассказать немного о будущем математической нотации.

Какой, к примеру, должна бы быть новая нотация?

В какой-нибудь книге символов будет содержаться около 2500 символов, популярных в тех или иных областях и не являющимися буквами языков. И с правильным написанием символов, многие из них могли бы идеально сочетаться с математическими символами.

Для чего же их использовать?

Первая приходящая на ум возможность — нотация для представления программ и математических операций. В Mathematica, к примеру, представлено довольно много текстовых операторов, используемых в программах. И я долгое время считал, что было бы здорово иметь возможность использовать для них какие-то специальные символы вместо комбинаций обычных символов ASCII [последние версии Mathematica полностью поддерживают Unicode — прим. ред.].

Оказывается, иногда это можно реализовать весьма просто. Поскольку мы выбрали символы ASCII, то часто можно получить некоторые символы, очень близкие по написанию, но более изящные. К примеру, если в Mathematica набрать ->, то эта стрелочка автоматически превратиться в более изящную . И это всё реализуемо за счёт того, что парсер в Mathematica может работать в том числе и со специальными символами.

Я часто размышлял о том, как бы расширить всё это. И вот, постепенно появляются новые идеи. Обратите внимание на знак решётки #, или номерной знак, или, как его ещё иногда называют, октоторп, который мы используем в тех местах, в которые передаётся параметр чистой функции. Он напоминает квадрат с щупальцами. И в будущем, возможно, он будет обозначаться симпатичным квадратиком с маленькими засечками, и будет означать место для передачи параметра в функцию. И он будет более гладким, не похожим на фрагмент обычного кода, чем-то вроде пиктограммы.

Насколько далеко можно зайти в этом направлении — представлении вещей в визуальной форме или в виде пиктограмм? Ясно, что такие вещи, как блок-схемы в инженерии, коммутативные диаграммы в чистой математике, технологические схемы — все хорошо справляются со своими задачами. По крайней мере до настоящего момента. Но как долго это может продолжаться?

Не думаю, что уж очень долго. Думаю, некоторые приближаются к некоторым фундаментальным ограничениям людей в обработке лингвистической информации.

Когда языки более или менее контекстно-свободные, имеют древовидную структуру, с ними можно многое сделать. Наша буферная память из пяти элементов памяти и что бы то ни было спокойно сможет их разобрать. Конечно, если у нас будет слишком много вспомогательных предложений даже на контекстно-свободном языке, то будет вероятность исчерпать стековое пространство и попасть впросак. Но, если стек не будет заходить слишком глубоко, то всё будет работать как надо.

Но что насчёт сетей? Можем ли мы понимать произвольные сети? Я имею в виду — почему у нас должны быть только префиксные, инфиксные, оверфиксные операторы? Почему бы операторам не получать свои аргументы через какие-то связи внутри сети?

Меня особенно интересовал этот вопрос в контексте того, что я занимался некоторыми научными вопросами касательно сетей. И мне действительно хотелось бы получить некоторое языковое представление для сетей. Но не смотря на то, что я уделил этому вопросу довольно много времени — не думаю, что мой мозг смог бы работать с подобными сетями так же, как с обычными языковыми или математическими конструкциями, имеющими одномерную или двумерную контекстно-свободную структуру. Так что я думаю, что это, возможно, то место, до которого нотация не сможет добраться.

Вообще, как я упоминал выше, это частый случай, когда язык или нотация ограничивают наше пространство мыслимого.

Итак, что это значит для математики?

В своём научном проекте я разрабатывал некоторые основные обобщения того, что люди обычно относят к математике. И вопрос в том, какие обозначения могут быть использованы для абстрактного представления подобных вещей.

Что ж, я не смог пока что полностью ответить на этот вопрос. Однако я обнаружил, что, по крайней мере в большинстве случаев, графическое представление или представление в виде пиктограмм гораздо эффективнее обозначений в виде конструкций на обычных языках.

Возвращаясь к самому началу этого разговора, ситуация напоминает то, что происходило тысячи лет в геометрии. В геометрии мы знаем, как представить что-то в графическом виде. Ещё со времён древнего Вавилона. И чуть более ста лет назад стало ясно, как можно формулировать геометрические задачи с точки зрения алгебры.

Однако мы всё ещё не знаем простого и ясного способа представлять геометрические схемы в обозначениях на естественном языке. И моя догадка состоит в том, что практически все эти математические вещи лишь в небольшом количестве могут быть представлены в обозначениях на естественном языке.

Однако мы — люди — легко воспринимаем лишь эти обозначения на естественном языке. Так что мы склонны изучать те вещи, которые могут быть представлены этим способом. Конечно, подобные вещи не могут быть тем, что происходит в природе и вселенной.

Но это уже совсем другая история. Так что я лучше закончу на этом.

Большое спасибо.

---

В ходе обсуждения после выступления и во время общения с другими людьми на конференции возникло несколько моментов, которые следовало бы обсудить.

Эмпирические законы для математических обозначений

При изучении обычного естественного языка были обнаружены различные историко-эмпирические законы. Пример —

Закон Гримма

, которые описывает переносы в согласных на индоевропейских языках. Мне было любопытно, можно ли найти подобные историко-эмпирические законы для математического обозначения.

Дана Скотт предложила такой вариант: тенденция к удалению явных параметров.

Как пример, в 60 годах 19 века часто каждый компонент вектора именовался отдельно. Но затем компоненты стали помечать индексами — как a_i. И вскоре после этого — в основном после работ Гиббса — векторы стали представлять как один объект, обозначаемый, скажем, как или a.

С тензорами всё не так просто. Нотацию, избегающую явных индексов, обычно называют координатно-свободной. И подобная нотация — частое явление в чистой математике. Однако в физике данный подход считается слишком абстрактным, потому явные индексы используются повсеместно.

В отношении функций так же имеется тенденция явно не упоминать параметры. В чистой математике, когда функции рассматриваются через сопоставления, они часто упоминаются лишь по своему имени — просто f, без каких-либо параметров.

Однако это будет хорошо только тогда, когда у функции только один параметр. Когда параметров несколько, обычно становится непонятно, как будут работать те потоки данных, которые ассоциированы с параметрами.

Однако, ещё в 20-х годах 20 века было показано, что можно использовать так называемые комбинаторы для определения подобных потоков данных без какого-либо явного указания параметров.

Комбинаторы не использовались в основных течениях математики, однако время от времени становились популярными в теории вычислений, хотя их популярность заметно поубавилась из-за несовместимости с идеей о типах данных.

Комбинаторы довольно легко задать в Mathematica через задание функции с составным заголовком. Вот как можно определить стандартные комбинаторы:

k[x_][y_]:=i x
s[x_][y_][z_]:= x[z][y[z]]

Если определить целое число n, по сути, в унарной системе, используя Nest[s[s[k[s]][k]],k[s[k][k]],n], то тогда сложение можно будет определить как s[k[s]][s[k[s[k[s]]]][s[k[k]]]], умножение как s[k[s]][k], а степень — s[k[s[s[k][k]]]][k]. Никакие переменные не требуются.

Проблема заключается в том, что выражения получаются непонятными, и с этим ничего не поделать. Я пытался найти какие-то способы для более ясного представления их и сопряжённых с ними вычислений. Я добился небольшого прогресса, однако нельзя сказать, что задача была решена.

Печатные обозначения против экранных

Некоторые спрашивали о разнице в возможностях печатных и экранных обозначений.

Чтобы можно было понимать обозначения, они должны быть похожими, и разница между ними не должна быть очень большой.

Но есть некоторые очевидные возможности.

Во-первых, на экране легко можно использовать цвет. Можно было бы подумать, что было каким-то образом удобно использовать разные цвета для переменных. Мой опыт говорит о том, что это удобно для разъяснения формулы. Однако всё станет весьма запутанным, если, к примеру, красному x и зелёному x будут соответствовать разные переменные.

Другая возможность состоит в том, чтобы иметь в формуле какие-то анимированные элементы. Полагаю, что они будут столь же раздражающими, как и мигающий текст, и не будут особо полезными.

Пожалуй, идея получше — иметь возможность скрывать и разворачивать определённые части выражения — как группы ячеек в ноутбуке Mathematica. Тогда будет возможность сразу получить представление обо всём выражении, а если интересны детали, то разворачивать его далее и далее.

Письменные обозначения

Некоторые могли бы подумать, что я уж слишком много времени уделил графическим обозначениям.

Хотелось бы прояснить, что я нахожу довольно затруднительным графические обозначения обычных математических действий и операций. В своей книге A New Kind of Science я повсеместно использую графику, и мне не представляется никакого другого способа делать то, что я делаю.

И в традиционной науке, и в математике есть множество графических обозначений, которые прекрасно работают, пускай и в основном для статичных конструкций.

Теория графов — очевидный пример использования графического представления.

К ним близки структурные диаграммы из химии и диаграммы Фейнмана из физики.

В математике имеются методы для групповых теоретических вычислений, представленные отчасти благодаря Предрагу Цвитановицу, и вот они основаны на графическом обозначении.

И в лингвистике, к примеру, распространены диаграммы для предложений, показывающие дерево лингвистических компонентов и способы их группировки для образования предложения.

Все эти обозначения, однако, становятся малопригодными в случаях исследования каких-то очень крупных объектов. Однако в диаграммах Фейнмана обычно используется две петли, а пять петель — максимум, для которого когда-либо были сделаны явные общие вычисления.

Шрифты и символы

Я обещал рассказать кое-что о символах и шрифтах.

В Mathematica 3 нам пришлось проделать большую работу чтобы разработать шрифты для более чем 1100 символов, имеющих отношение к математической и технической нотации.

Получение правильной формы — даже для греческих букв — часто было достаточно сложным. С одной стороны, мы хотели сохранить некоторую традиционность в написании, а с другой — сделать греческие буквы максимально непохожими на английские и какие бы то ни было другие.

В конце концов я сделал эскизы для большинства символов. Вот к чему мы пришли для греческих букв. Мы разработали Times-подобный шрифт, моноширинный наподобие Courier, а сейчас разрабатываем sans serif. Разработать шрифт Courier было непростой задачей. Нужно, к примеру, было придумать, как сделать так, чтобы йота занимала весь слот под символ.

Так же сложности были со скриптовыми и готическими (фактурными) шрифтами. Часто в этих шрифтах буквы настолько непохожи на обычные английские, что становятся абсолютно нечитаемыми. Мы хотели, чтобы эти шрифты вписывались в соответствующую им тему, и, тем не менее, обладали бы теми же габаритами, что и обычные английские буквы.

Вот, что у нас получилось:

Веб сайт fonts.wolfram.com, в котором собрана вся детальная информация о символах и шрифтах, разумеется, если они имеют отношение к Mathematica и её шрифтам.

Поиск математических формул

Некоторые люди спрашивали о поиске математических формул [после создания Wolfram|Alpha появился гигантский объем баз данных, доступных в языке Wolfram Language, теперь можно получить огромный массив информации о любых формулах с помощью функции

MathematicalFunctionData

— прим. ред.].

Очевидно легко сказать, что же такое поиск обычного текста. Единственная вопрос заключается в эквивалентности строчных и прописных букв.

Для математических формул всё сложнее, потому что есть ещё много различных эквивалентностей. Если спрашивать о всех возможных эквивалентностях, то всё станет слишком сложным. Но, если спросить об эквивалентностях, которые просто подразумевают замену одной переменной другой, то всегда можно определить, эквивалентны ли два выражения.

Однако, для этого потребуется мощь обнаружителя одинаковых паттернов Mathematica.

Мы планируем встроить возможности по поиску формул в наш сайт functions.wolfram.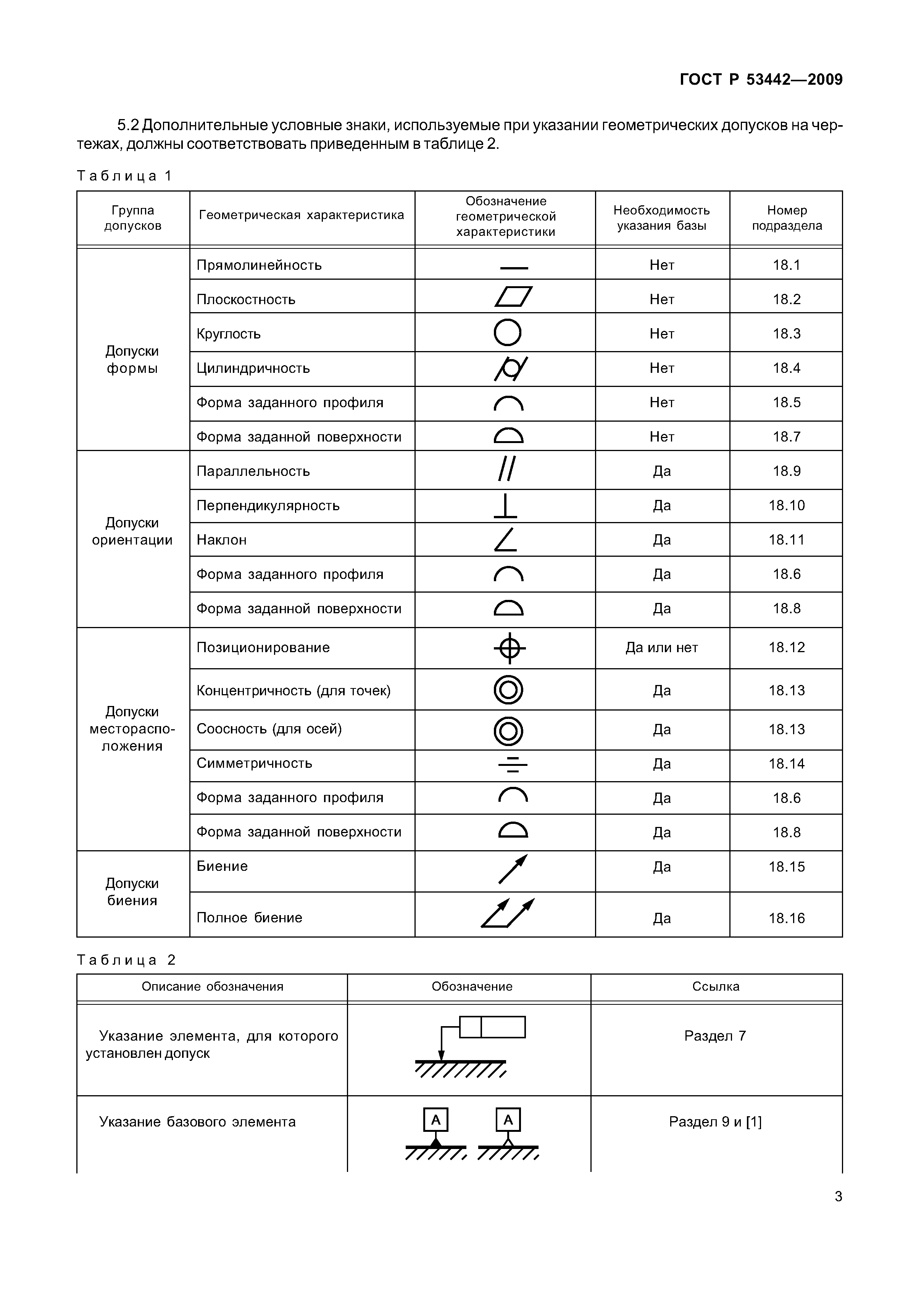 com, однако тут я не буду останавливаться на подробностях.

Невизуальные обозначения

Кто-то спрашивал о невизуальных обозначениях.

Первая мысль, которая у меня возникла, заключалась в том, что человеческое зрение даёт гораздо больше информации, чем, скажем, слух. В конце концов, с нашими глазами соединён миллион нервных окончаний, а с ушами лишь 50 000.

В Mathematica встроены возможности по генерации звуков начиная со второй версии, которая была выпущена в 1991 году. И были некоторые моменты, когда эта функция оказывалась полезной для понимания каких-то данных.

Однако я никогда не находил подобную функцию полезной для чего-то, связанного с обозначениями.

Доказательства

Кто-то спрашивал о представлении доказательств.

Самая большая проблема заключается в представлении длинных доказательств, которые были автоматически найдены с помощью компьютера.

Большое количество работы было проделано для представления доказательств в Mathematica. Примером является проект Theorema.

Самые сложные для представления доказательства — скажем, в логике — представляют из себя некоторую последовательность преобразований. Вот пример такого доказательства:

Даны аксиомы Шеффера для логики (f это NAND):

{f[f[a,a],f[a,a]]==a,f[a,f[b,f[b,b]]]==f[a,a], f[f[a,f[b,c]],f[a,f[b,c]]]==f[f[f[b,b],a],f[f[c,c],a]]}

Доказать коммутативность, то есть что f[a,b]==f[b,a]:

Замечание (a b) есть Nand[a,b]. В этом доказательстве L == лемма, A == аксиома, и T == теорема.

Отбор символов

Я хотел бы кое-что рассказать о выборе символов для использования в математической нотации.

Существует около 2500 часто используемых символов, которые не встречаются в обычном тексте.

Некоторые из них слишком картинны — скажем, обозначение для хрупких предметов. Некоторые слишком витиеватые. Некоторые полны чёрной заливки, так что они будут слишком сильно выделяться на странице (символ радиации, например).

Но некоторые могут быть вполне приемлемыми.

Если заглянуть в историю, часто можно наблюдать картину, как со временем написание некоторых символов упрощается.

Особой проблемой, с которой я не так давно столкнулся, был выбор хорошего обозначения для таких логических операций, как NAND, NOR, XOR.

В литературе по логике NAND обозначается по-разному:

Ни одно из этих обозначений мне особо не нравилось. В основном они наполнены тонкими линиями и недостаточно цельны для того, чтобы представлять бинарные операторы. Однако они передают своё содержание.

Я пришёл к следующему обозначению для оператора NAND, который основан на стандартном, однако имеющим улучшенную визуальную форму. Вот текущая версия того, к чему я пришёл:

Частотное распределение символов

Я упоминал о частотном распределении греческих букв в MathWorld.

В дополнение к этому я также посчитал количество различных объектов, именуемых с помощью букв, которые появляются в словаре физических терминов и математических сокращений.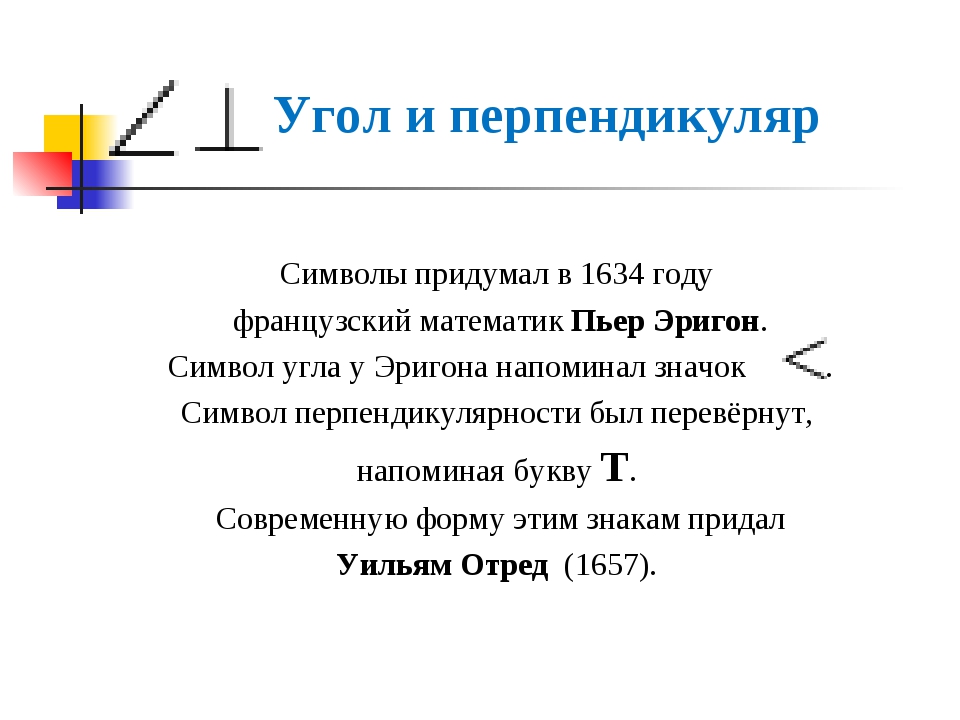 Вот результаты.

В более ранних образцах математической нотации, скажем, в 17 веке, обычные слова шли вперемешку с различными символами.

Однако всё более в таких сферах, как математика и физика, проявлялась тенденция к исключению слов из обозначений и именования переменных одной или двумя буквами.

В некоторых областях инженерии и социальных наук, куда математика дошла не так давно и не является слишком абстрактной, обычные слова гораздо чаще можно встретить в качестве имён переменных.

Та же история с современными тенденциями в программировании. И всё работает хорошо, пока формулы достаточно просты. Однако по мере усложнения формул нарушается их визуальный баланс, и становится уже сложно разглядеть их общую структуру.

Части речи в математической нотации

В разговоре о соответствии языка математики и обычного языка я хотел упомянуть вопрос частей речи.

Насколько я знаю, во всех обычных языках есть глаголы и существительные, и в большинстве из них есть прилагательные, наречия и др.

В математической нотации можно представлять переменные как существительные и глаголы как операторы.

А что насчёт других частей речи?

Вещи наподобие иногда играют роль союзов, как и в обычных языках (примечательно, что во всех языках есть отдельные слова для AND и OR, однако ни в одном нет слова для NAND). А в качестве префиксного оператора может рассматриваться как прилагательное.

Однако не до конца ясно, в какой мере различные виды лингвистических структур, связанные с частями речи на обычном языке, отражены в математическом обозначении.

По вопросам о технологиях Wolfram пишите на [email protected]

определение угла, измерение углов, обозначения и примеры. Видео как поставить знак угла в программе word

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .

На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .

Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .

Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.

Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Определение 5

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Определение 6

Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.

На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.

Определение 7

Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.

При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.

Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.

Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.

Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .

Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.

Развернутые углы являются равными.

Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу.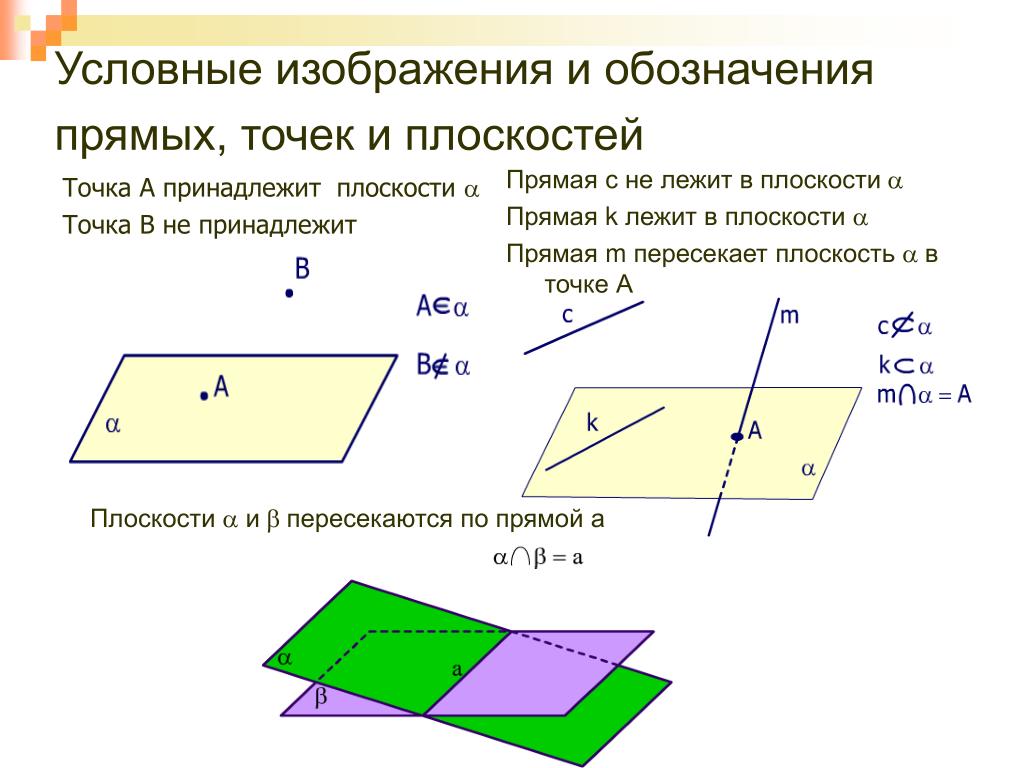 Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.

Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.

Чаще всего используют понятие градус .

Определение 8

Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.

Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.

Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.

Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.

Определение 9

Минутой называют одну шестидесятую часть градуса.

Определение 10

Секундой называют одну шестидесятую часть минуты.

Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:

1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,

а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .

Определение 11

Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .

Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».

В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.

Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.

Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .

Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.

Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.

Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.

Определение 12

Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.

На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.

Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.

Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.

На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.

Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.

Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.

Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Если в документах Microsoft Word Вам приходиться работать не только с текстом, но иногда необходимо показать элементарные расчеты, или вставить в текст определенный символ, тогда не найдя его на клавиатуре, Вы зададитесь вопросом: как добавить его в документ?

Сделать это довольно просто, поскольку в текстовом редакторе Ворд есть специальная таблица, в которой Вы точно найдете все необходимое. В данной статье мы с Вами рассмотрим, как, используя ее, можно вставить в документ Ворд примерно равно.

Установите курсор в том месте документа, куда будете его добавлять. Затем перейдите на вкладку «Вставка» и в группе «Символы» нажмите на одноименную кнопку. В выпадающем списке выберите пункт «Другие» .

Откроется вот такое окно. В нем в поле «Шрифт» выберите «(обычный текст)» , в поле «Набор» – «математические операторы» . Дальше найдите в списке то, что нужно, кликните по нему и затем нажмите кнопку «Вставить» .

После того, как значок будет добавлен в документ, закройте данное окно, нажав на соответствующую кнопку в правом нижнем углу.

Если Вам часто приходится добавлять в документ различные знаки, которые напечатать напрямую с клавиатуры не получится, и приходится искать их в упомянутой таблице, тогда можете воспользоваться горячими клавишами, для вставки подходящего знака в документ.

Найдите символ в списке и кликните по нему мышкой. Затем внизу в поле «Сочетание клавиш» посмотрите, какая комбинация для него используется.

В нашем случае, это «2248, Alt+X» . Сначала наберите число «2248» , а потом нажмите «Alt+X» .

Замечу, что не для всех знаков есть сочетания, но его можно назначить самостоятельно, кликнув по кнопке «Сочетание клавиш» .

Если у Вас, как и в примере, знак приблизительно нужно поставить сразу после какой-нибудь цифры, то сочетание получится другое. В примере получилось «32248» .

Поэтому, после того, как Вы нажмете «Alt+X» , может вставится не то, что Вы хотите.

Для того чтобы добавить именно приблизительно-равно, поставьте пробел после той цифры, где он должен стоять и наберите сочетание «2248» . Затем нажимайте «Alt+X» .

Символ будет вставлен. Теперь можно поставить курсив перед добавленным знаком и нажать «Backspace» , чтобы удалить пробел.

Вот так, используя один из способов, можно поставить значок приблизительно равно в документ Ворд.

Оценить статью:

В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.

Навигация по странице.

Определение угла.

Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .

Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.

Дадим сначала определение луча.

Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .

Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.

Теперь мы можем дать первое определение угла.

Определение.

Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .

Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.

Определение.

Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .

Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.

Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k , а другая h ), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA , а вторая сторона угла OB ), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1 , 2 и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.

Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.

Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.

Определение внутренней области угла приводит нас ко второму определению угла.

Определение.

Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.

Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).

Дадим еще определения смежных и вертикальных углов.

Определение.

Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.

Из определения следует, что смежные углы дополняют друг друга до развернутого угла.

Определение.

Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.

На рисунке изображены вертикальные углы.

Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.

Сравнение углов.

В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.

Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.

Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?

Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .

Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).

Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.

Измерение углов.

Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.

Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.

Одной из единиц измерения углов является градус .

Определение.

Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.

Градус обозначают символом «», следовательно, один градус обозначается как .

Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.

При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).

Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.

Определение.

Минута – это одна шестидесятая часть градуса.

Определение.

Секунда – это одна шестидесятая часть минуты.

Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .

Определение.

Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.

Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .

Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.

Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».

Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.

Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. На рисунке ниже показан угол АОВ , который составляют углы АОС , СОD и DОВ , при этом .

Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.

Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .

Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.

Определение.

Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.

Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.

Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.

Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.

Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.

Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.

Обозначение углов на чертеже.

На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.

Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.

Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.

Список литературы.

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
• Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.

Очень часто слышу вопрос «Как получитьсимвол галочки в Ворде?» Ответы — один мудренее другого! Проще всего нажать клавишу Альт и, не отпуская её, набрать на боковой цифровой клавиатуре число 10003. Можно так же набрать число 2713 и потом нажать Альт икс. Просто оба эти числа равны между собой: 10003 (десятичное) = 2713 (шестнадцатиричное).

Когда много работаешь в программах Ворд и Ексель, начинаешь понимать, что бросать клавиатуру, хвататься за мышь, а потом снова переходить к «клаве» — неудобно, неэргономично, не… — продолжите сами. Наверное для этого и придуманы разные сочетания кнопок, «горячие» клавиши и т.п. В этом плане мне очень нравится функциональная клавиша F4, нажатие на которую повторяет любое действие, которое только что выполнялось. Например, вам надо 8 слов в разных местах текста выделить полужирным шрифтом. Первое слово вы можете сделать сделать «жирным» щелкнув по букве » ж » в меню или нажав одновременно две клавиши Ctrl и b (русская буква и). Для остальных слов достаточно правой рукой щелкнуть мышью по любому месту в нужном слове, а левой рукой нажать клавишу F4. «И так сэм раз».

Многие вздрагивают при слове «макрос», а между тем в них нет ничего страшного и опасного. Вообще, макросы — это очень полезная вещь! Создать макрос в Ворде — проще простого. Допустим, вам часто требуется при наборе текста вставлять название организации: ООО «Рога и Копыта» . Или печатать в конце документа: Исполнитель — Вася Пупкин . Рассмотрим, как набрать первый текст нажатием всего двух клавиш, а второй — одним нажатием на кнопку с любым рисунком, созданную на панели быстрого доступа.

Итак, давайте попробуем: открываем Ворд и выбираем «Сервис-Макросы» или «Вид-Макросы» (в зависимости от того 2003-й или 2007-й) и жмем «Запись макроса…». В появившемся окне можно придумать название макросу и сделать его описание, но можно оставить предложенное по умолчанию название «Макрос1» и ничего не описывать — кому как нравится. Но нажать на значок с изображением клавиатуры или молотка надо обязательно. В первом случае вам будет предложено придумать любое сочетание клавиш, а во втором — кнопку на панели. Для первого текста выбираем сочетание Ctrl+P (что бы легче вспомнить, берем первую букву Рогов), затем нажимаем «Назначить» и «Закрыть». Окно при этом исчезает, а рядом с курсором появляется пиктограмма магнитофонной кассеты, это означает, что «все ходы записываются». В 2003-м Ворде при этом еще появляется малюсенькая плавающая панель. В первый и последний раз (потом это за вас будет делать компьютер) набираем нужный текст с названием фирмы и останавливаем запись. В старом Ворде — просто нажав квадратик на плавающей панели, а в новом — зайдя в меню «Вид-Макросы-Остановить запись». Теперь и всегда (до переустановки Офиса или удаления макроса) нажатие выбранного вами сочетания клавиш выдаст вам то, что вы набрали во время записи макроса.

Если на начальной стадии вы нажмете на молоток, то в 2003-м появится окно Настройка со стандартным значком макроса, который надо, схватив мышкой, перетащить в любое место верхней панели меню, а затем, щелкнув по кнопке «Изменить выделенный объект» и по строке «Выбрать значок для кнопки» выбрать смайлик или любой понравившийся вам рисунок. Если же нажать на строку «Изменить значок на кнопке…», то откроется простенький графический редактор, в котором можно самому нарисовать значок на свой вкус.

В 2007-м похожий путь: при выборе молотка появляется Настройка панели быстрого доступа, где надо, выделив в левом окошке макрос и нажать кнопку «Добавить». После этого стандартный значок макроса с вашим названием добавится в правое окно, где его можно снова выделить и нажать кнопку «Изменить». Выбор рисунков будет побольше, чем в старом Ворде, но зато убрана возможность нарисовать свой значок и размещать его можно только на панели быстрого доступа.

Дальнейшие действия такие же, что и в 2003-м: набор нужного текста и остановка записи. Подобных макросов можно наделать сколько угодно, в результате вы получите возможность одним щелчком по вашему значку (которого, заметьте, нет ни у кого из ваших коллег!) получать нужный текст или любую последовательность операций.

Как и что надо набрать на клавиатуре, чтобы получить в текстовом документе изображение сердечка? Проще всего нажать клавишу Alt и не отпуская её нажать цифру 3 на правой части клавиатуры. Другой способ: набрать число 2665 и нажать сочетание клавиш Alt+х. Так же для получения сердечек можно набрать числа 2765, 2764 или 2661. Очень похожа на сердечко одна из букв грузинского алфавита ღ, получить которую можно набрав код 10Е5 (Е — латинское) и нажав Alt+х.

Вообще для получения любого символа достаточно набрать его ASCII -код и нажать Alt+х. Например, чтобы напечатать знак доллара «$», проще и быстрее не переходя на английский шрифт набрать число 24, а затем нажать Alt+х. Можно быстро получить знак суммы «∑» (код — 2211), символ угла «∠» (код — 2220), приблизительного равенства « ≈ » (код — 2248), различные стрелки и т.д. Именно поэтому иногда вместо слова «собака» говорят «сорок альт икс» имея ввиду @.

Вот таблица кодов некоторых символов:

Код	Символ	Код	Символ	Код	Символ	Код	Символ
23	#	2020	†	2194	↔	2265	≥
24	$	2030	‰	2195	↕	2640	♀
26	&	2122	™	2211	∑	2642	♂
27	»	2190	←	2220		2660	♠
40	@	2191		2248	≈	2663	♣
60	`	2192	→	2260	≠	2665
394	Δ	2193	↓	2264	≤	2666	♦

Сила символов в дизайне

Символизм (также называемый семиотикой) — эффективный инструмент коммуникации. Это способ передачи слишком сложных идей, которые трудно выразить словами, позволяющий нам общаться, несмотря на языковые барьеры. Графический дизайн, который представляет собой коммуникацию посредством узнаваемых образов, постоянно обращается к символизму.

Иллюстрация OrangeCrush

Символы настолько укоренились в нашем культурном сознании, что мы часто используем их, даже не задумываясь. Иногда они являются такими старыми или непонятными, что мы с легкостью забываем их значение. В графическом дизайне это может стать проблемой: чтобы эффективно использовать символы в своей работе, дизайнеры должны понимать идеи, лежащие в их основе, иначе может возникнуть ситуация, когда результат будет транслировать совсем не тот смысл, который закладывал автор.

Чтобы этого не произошло и вы смогли пустить в ход древнюю силу символов, мы представляем вам обзор истории самых распространенных символов, их значений и современных вариантов применения символизма в дизайне.

Что такое символизм?

Символизм — это использование письменных знаков, форм, изображений и/или физических объектов, имеющих определенное значение. Их можно найти повсюду. Например, буквы, из которых составлены слова на этой странице, технически тоже являются символами: мы все согласны с тем, что эти абстрактные значки отражают звуки человеческой речи.

Ценность символов заключается в том, что они позволяют визуально выразить смысл. Например, всем понятно, что красный восьмиугольник на дороге означает “Стоп”. Такой символ может спасать жизни, ведь неудобно читать длинные слова на высокой скорости. Часто подразумеваемый смысл может быть намного сложнее и не ограничиваться одним словом, в этом случае символы упрощают и ускоряют понимание. Вот почему графические дизайнеры используют символы для визуальной коммуникации.

Автор: tilleri

Графические дизайнеры, зачастую, используют в своей работе распространенные символы, но также и создают новые, оригинальные. Например, при разработке логотипа цель состоит в том, чтобы создать уникальное графическое обозначение, которое отражает суть бренда. Чтобы сделать это эффективно, необходимо понимать историю возникновения распространенных символов и то, какую роль в визуальном языке они играли в разное время.

На протяжении истории человечества появилось множество символов. В этой статье мы сгруппируем их в три общие категории, рассмотрим некоторые конкретные примеры и обсудим, каким образом современные дизайнеры присваивают им новые значения.

Символы природы

Изображения животных настолько часто встречаются в наскальных рисунках, что становится понятно: первобытные люди воспринимали свою жизнь через призму взаимодействия с природой. Несмотря на развитие цивилизации и технологий, такой подход в определенной мере сохраняется до сих пор — в основе почти всех символов лежит почтение к силам природы. Давайте рассмотрим несколько распространенных категорий таких природных символов и способы их использования в проектах.

Совы — один из примеров использования изображений животных как символов, обычно олицетворяют мудрость. Дизайн логотипа artsigma.

Анималистические символы и средневековая геральдика

Использование изображений животных в качестве символов обычно предполагает наделение их конкретными человеческими качествами. Присвоение животным таких качеств происходило на протяжении тысячелетий в мифах и историях: коварный змей в Книге Бытия, грациозный лебедь из Сказок братьев Гримм, медлительная спокойная черепаха из Басен Эзопа. Многие из этих качеств интуитивно понятны (хотя и могут различаться в зависимости от культуры), например, в западных культурах:

Пример средневековой геральдики. Изображение с wikimedia commons.

• Львы символизируют королевскую власть
• Голуби символизируют мир
• Быки символизируют гнев
• Совы символизируют мудрость
• Собаки символизируют преданность
  

Такие символы приобрели особую популярность, благодаря средневековой геральдике, когда на щитах и флагах можно было увидеть гербы, показывающие принадлежность к определенной группе. Хотя применялись все виды иконографии (особенно религиозной), чаще всего на гербах изображали львов, орлов, волков, медведей, оленей и даже мифологических существ, таких как грифоны или драконы. Все они были окружены декоративными цветочными элементами. Эта традиция сохранилась и в современном дизайне флагов: многие государства и страны выбирают определенных животных в качестве своих символов.

В настоящее время дизайнеры иногда находят новое применение средневековой геральдике, работая с брендами — конкурирующими сторонами в современном контексте. Поскольку гербы представляют собой архаичные символы, их использование наиболее эффективно для брендов, которые следуют традициям, например, семейных бизнесов или тех, чья деятельность является классической, как, например, виноделие. Хотя дизайнеры обычно отдают предпочтение традиционным иллюстрациям, они также используют современные техники, например, монолинии, как Skilline на картинке ниже, что позволяет объединить прошлое и настоящее.

Важно то, что, вдумчиво используя изображения животных в качестве символов, дизайнеры передают в своих работах конкретные уникальные личностные черты.

Автор: YokaonaАвтор: SkillineАвтор: austinminded   Автор: Eliza Osmo

Использоваться может не только образ животного в целом, но и отдельные части тела, также обладающие символическим значением. Крылья часто обозначают свободу, рога могут демонстрировать власть (поскольку похожи на корону), а лапы, когти или бивни символизируют силу.

Растения как символы

Лавр часто используется как символ победы и достижений. Дизайн логотипа anton-p.

Растения-символы часто наделяются значениями, связанными с ростом, такими как обновление, спокойствие и  устремление. Некоторые символы берут свое начало в поклонении природе, которое было распространено в древних религиях, как, например, кельтское дерево жизни. Но как и в случае с животными, многие растения исторически ассоциировались с определенными качествами, например:

• Оливковая ветвь — символ мира
• Трехлистный клевер — символ удачи
• Роза — символ любви
• Лилия — символ скорби
• Лавр — символ победы
  

Растительные элементы также могут занимать центральное место на гербе. Дизайн DariaR.

В геральдике растения часто использовались в декоративных целях. Аналогичным образом современные дизайнеры, как правило, делают извилистые лозы и корни элементами обрамления. Однако некоторые растения занимали именно центральное место на гербах, например, роза в Англии и геральдическая лилия во Франции (обе символизировали монархию). Важно учитывать подобные средневековые ассоциации, работая над гербом, содержащим растительные элементы.

Изображения лотоса часто используют бренды, осуществляющие деятельность в сфере здоровья. Дизайн логотипа vraione.

Один из наиболее известных растительных символов нашего времени — цветок лотоса. В индуистской и буддистской традиции он символизирует божественную чистоту, поэтому часто богов изображают сидящими или стоящими на одном из цветков лотоса. Его также можно увидеть раскрытым с симметричными лепестками, которые обозначают разные чакры, энергию, поддерживающую человеческую жизнь. Такие ассоциации сделали лотос популярным символом в искусстве и дизайне, связанном с темами здоровья и благополучия.

Четыре стихии и знаки зодиака

Символы природы в дизайне обычно используются для изображения гармонии и баланса, другими словами, показывают природу как взаимозависимую экосистему. Эту идею воплощают четыре символа стихий: земля, вода, огонь и воздух. Вместе указанные элементы способны вызвать Капитана Планету (герой американского мультфильма)… а точнее, создают ощущение благополучия и целостности. При этом каждый из них обладает собственными характеристиками: земля — надежная и стабильная, вода — прохладная и успокаивающая, воздух — легкий и подвижный, огонь — динамичный и сильный. Дизайнеры часто изображают эти элементы с помощью цветов и/или абстрактных линий.

Природные элементы и их атрибуты находят более конкретное выражение в знаках зодиака. Хотя в основе таких знаков лежат созвездия, каждый из них также соответствует определенному животному и одному из четырех элементов:

• Знаки земли: Телец, Близнецы, Козерог.
• Знаки воды: Рак, Скорпион, Рыбы.
• Знаки воздуха: Близнецы, Весы, Водолей.
• Знаки огня: Овен, Лев, Стрелец.
  

Дизайн, включающий определенный знак зодиака, будет вызывать связанные с его особенностями ассоциации. Дизайнеры часто используют знаки зодиака — как изображения животных, так и цвета стихий — чтобы лучше выразить идею своей работы.

Знаки зодиака наполнены символизмом природы, что может пригодиться в дизайне. Упаковка разработана brandstrategy.

Богини как символы

Растения и животные — наиболее распространенные символы природы, однако долгое время именно люди или, точнее, боги и богини в человеческом обличье, олицетворяли силы природы. Известные примеры: Артемида, Пан, Гея. Чаще всего, их изображают не по отдельности, а как единое целое — богиню, известную как Мать-природа. В настоящее время дизайнеры используют изображения богинь как символ благословения, мудрости и силы природного мира.

Автор GoodEnergyАвтор svart inkАвтор ArdaАвтор C1k

Астрономические символы

Сегодня мы знаем, что ночное небо — это просто часть природы, однако длительное время люди так не считали. Небесный мир воспринимался как далекий, загадочный, а по ночам как наполненный таинственными знаками и символами. По этой причине астрономические символы до сих пор зачастую выражают в дизайне тайну или сверхъестественное предзнаменование. Давайте рассмотрим наиболее распространенные из них.

Канцтовары с небесными объектами, Алина Гронская на Behance

Изображение солнца

Поскольку солнце — это источник света и наиболее важное небесное тело, оно является одним из самых главных астрономических символов и часто ассоциируется с королевской властью. На протяжении многих веков его изображали как идеальный диск с точкой в середине, круг при этом символизировал цикл, который проходит солнце от восхода до заката. Позднее солнце стали рисовать как сферу с крестом в центре, чтобы показать четыре сезона года. Индуистская свастика была производной от этой версии.

В конце концов, греки придумали Вергинское солнце, которое легло в основу общеизвестного символа солнца, привычного для нас сегодня: золотой круг с выходящими из него треугольными лучами. Намного позднее средневековые рыцари дорисовали солнцу лицо и создали геральдическую эмблему с чередующимися прямыми и волнистыми лучами, которую использовали для украшения щитов.

Автор Taynara Lima, BehancАвтор spARTan Автор Vulcan” Автор coric design

В современных дизайнах солнце чаще всего символизирует силу и радость. Хотя солнце в том варианте, в каком его придумали средневековые рыцари, приобрело новую популярность благодаря эмодзи, оно по-прежнему придает дизайнам легкий геральдический оттенок.

Изображение луны

Луна одновременно выступает и как противоположность солнца, и как дополнение к нему. Солнце ассоциируется с золотом, луна — с серебром, солнце наделяется мужскими чертами, а луна — женскими. Оба небесных тела циклически меняются, однако луна претерпевает более серьезные изменения каждый месяц. Именно по этой причине она и стала символом преобразования, трансформации.

Автор Arthean Автор PristiPerje Автор ✦ᎪᏞᎥᏟᎥᎪ✦

Самая знаковая из этих форм, полумесяц, символизировала луну на протяжении тысячелетий. Поскольку это форма, которую трудно было себе представить в небе, а увидеть ее можно лишь в холодной темноте ночи, обычно полумесяц ассоциируется с мистикой. Сегодня дизайнеры используют этот символ, если хотят придать бренду магический вид.

Но стоит помнить, что с того момента, как он был принят в качестве элемента средневековой геральдики Османской империи полумесяц, особенно в сочетании с утренней звездой, является символом ислама.

Изображения созвездий и планет

Созвездия в определенной степени связаны со знаками зодиака, но у многих из них также есть значения и названия, берущие начало в мифах, например, Орион и Большая Медведица. Чести быть увековеченными в названии созвездий часто удостаивались те мифологические персонажи, которые отличились героическим подвигом или жертвой.

Каждой планете также соответствует свой символ, чаще всего, обозначающий одноименного римского бога — например, символы Венеры и Марса легли в основу гендерных символов. Кроме того, любая планета обычно ассоциируется с определенным металлом. Дизайнеры могут использовать обе эти идеи в своих проектах.

   

Ссылка на картинку                                   Ссылка на картинку

Автор svart ink                                             Автор Made by Mystie

   

Автор bubo_scandiacus

В композиции созвездия могут эффективно играть роль фона или рамки, аналогично растительным элементам, которые обсуждались ранее. И наоборот, создавая контуры предметов с помощью звезд и соединяющих их линий, дизайнеры могут сделать свои проекты такими же мистическими, как и сами созвездия в описаниях историков прошлого.

Геометрические символы

Люди исторически рассматривали окружающий мир не только через призму природы и космологии, но и через повторяющиеся формы. Во многом это связано с распознаванием образов: люди от природы распознают повторяющиеся элементы в окружающем мире, при этом наиболее часто в качестве таких элементов выступают базовые геометрические формы.

Треугольники, пирамиды и всевидящее око

Простые геометрические фигуры обычно выражают чистоту и баланс, но при этом обладают множеством символических значений. Зачастую такие значения абстрактны и соответствуют самой форме: например, круги могут символизировать бесконечность, а квадраты — стабильность.

Треугольники позволяют передать в дизайне идею божественности. Лучи света, расходящиеся от центрального изображения, усиливают этот эффект. Дизайн логотипа разработан thedani.

Одной из наиболее значимых базовых форм является треугольник, а точнее его трехмерный аналог: пирамида.

Равносторонний треугольник по сути представляет собой стрелку, указывающую вверх, и обычно ассоциируется с чем-то божественным.

Вспомним о том, как в древние времена люди поклонялись священным горам, в том числе Олимпу, горе Синай и Фуджи. Древние Египтяне верили, что северный полюс мира в ночном небе является царством богов, а пирамиды специально верхушкой устремлены к нему, чтобы позволить умершим беспрепятственно отправиться на небеса.

Именно ассоциации с божественным послужили причиной того, что Всевидящее око стали изображать внутри треугольника и/или на вершине пирамиды, что символизирует одновременно идею божества, которое сверху наблюдает за всем, и архитектора вселенной. Возможно, к этому имеет отношение также и Глаз Гора, используемый в Древнем Египте для обозначения королевской власти.

Автор ludibesАвтор safer»Автор Sevarika™

В настоящее время глаз символизирует заговоры, поскольку его связывают с тайным масонским обществом и правительством США из-за изображения на долларовой банкноте. Многие дизайнеры используют символ Всевидящего ока, чтобы показать, что клиенты бренда станут частью подпольной контркультуры или получат доступ к эксклюзивным знаниям.

Сакральная геометрия

Если смысл базовых форм может заключаться в их простоте, то сложная геометрия требует математической точности. Математика во многих отношениях является фундаментальным выражением законов нашей Вселенной. Сакральная геометрия — это общий термин для всех геометрических символов, обладающих духовным смыслом. Ее можно воспринимать как изобретенный древними людьми способ визуализации и применения универсальной силы математических пропорций. В разных культурах встречается множество сакральных геометрических символов, но мы рассмотрим здесь лишь некоторые из них.

Изображение Инь и ян, WikipediaИзображение мандалы, WikipediaИзображение пентаграммы, Wikipedia

                 

Изображение куба Метатрона, WikipediaТреугольник Пенроуза, Wikipedia Анимация с золотой спиралью, Wikipedia

• Мандала может принимать различные формы, однако самый простой вариант состоит из квадрата, имеющего с четырех сторон Т-образные ворота, и бинду (центральной точки). Разные геометрические узоры, лепестки лотоса, цвета и/или изображения божеств располагаются вокруг бинду. Значение символа варьируется в зависимости от формы согласно индуистским писаниям. Мандала обычно помогает в медитации.
• Инь и ян использовался в Древнем Китае для обозначения взаимосвязи противостоящих сил с помощью идеально пропорциональных кривых.
• Пентаграмма или пятиконечная звезда изначально была религиозным символом и отражала различные католические идеи, например, пять радостей девы Марии. Позднее она стала знаком зла и оккультизма, особенно если звезда повернута вверх ногами таким образом, что два верхних луча напоминают рога дьявола.
• Куб Метатрона — помимо того, что он имеет интересное название, символ состоит из нескольких взаимосвязанных шестиугольников, треугольников и кругов, которые образуют трехмерный куб в центре. Аналогично Ящику Пандоры его часто воспринимают как вместилище божественных знаний, что также соответствует имени, которым назван куб (мудрый архангел Метатрон).
• Треугольник Пенроуза — не является священным символом и не связан напрямую с какой-то религией. Он был создан в 1930-х годах Оскаром Реутерсвардом и представляет собой одну из основных невозможных геометрических фигур.
• Золотая спираль, скорее всего, наиболее известна графическим дизайнерам. Это спираль, в основе построения которой лежит золотое сечение, обычно она используется в дизайне для определения пропорций и выстраивания композиции.
  

Автор aleT Автор betiobcaАвтор Carolina Crespo ✏Автор svart ink

Используя сакральную геометрию в определенном значении, дизайнеры должны сначала изучить возможные варианты изображения символа. Хотя такие фигуры воспринимаются просто как красивые и сложные и напоминают ювелирные украшения, помните, что они не зря называются сакральными.

Эти символы часто ассоциируются с определенными культурами и/или религиями, и вы должны помнить об этом и иметь достаточно веские основания, чтобы использовать их в своих проектах. Таким образом вы не только проявите уважение, но и предотвратите негативную реакцию покупателей на использование брендом культурных символов в коммерческих целях.

Если вы все сделали правильно и все-таки решили использовать сакральную геометрию, она поможет вам придать композиции ощущение порядка и баланса и выделить центральные изображения, например, иллюстрации.

Создайте свои символы и используйте их в дизайне

Как и любой вид коммуникации, графический дизайн опирается на символы. Хотя распространенные символы с известными значениями имеют долгую историю, задача дизайнера должна состоять не только в использовании этих символов в своих целях. Часто дизайнерам приходится создавать уникальный язык символов для какого-то бизнеса, чтобы покупатели могли с первого взгляда определить ценности компании и понять, что отличает ее от конкурентов.

Чтобы эффективно выполнить такую задачу, необходимо изучить уже существующие символы. Если вы хотите, чтобы дизайн вашего бренда включал символы, убедитесь, что вы работаете с талантливым дизайнером, который хорошо в них разбирается.

Символы | План-конспект занятия по математике:

Государственное автономное учреждение дополнительного профессионального   образования Липецкой области  

«Институт развития образования»

Конспект образовательной деятельности детей подготовительной группы                                               по ФЭМП (образовательная область «Познавательное развитие»)

Тема: «Символы»

                                                     

                                         

                                         Выполнила:                                                                 слушатель курсов профессиональной переподготовки

Сухинина Ольга Сергеевна

г. Липецк-2019

Тема «Символы».

Цель:

1. Познакомить детей с использованием символов для обозначения свойств предметов (цвет, форма, размер).

Материалы к занятию:

   Демонстрационный: геометрические фигуры разных цветов, формы и размера; карточки с изображением символов, обозначающих форму, цвет, размер. Плакат по ПДД.

   Раздаточный: геометрические фигуры, цветные и простые карандаши.

Ход занятия:

1. Формирование представлений о символах.

1. Организационно-мотивационный момент.

— Ребята, посмотрите! Сегодня к нам пришли гости. Давайте поздороваемся с ними (Здравствуйте!) А сейчас, дружно за руки возьмемся и друг другу улыбнемся, чтоб у нас было хорошее настроение, чтоб мы были умными, внимательными и чтоб у нас все получилось.

-Утром, когда я пришла в группу, я увидела странное письмо. Кто-то просунул к нам его под дверь. Хотите узнать, что в нем? (да). Давайте посмотрим. В нем лежит письмо с просьбой о помощи. Незнайку пригласили его друзья в гости, чтоб он нарисовал их портрет. А он боится в большом городе попасть в ДТП. Поможем Незнайке? (да). Дети подходят к плакату ПДД и рассказывают, как можно правильно, соблюдая правила дойти до его друзей.

-Молодцы ребята! Скажите пожалуйста, а что помогло нам правильно указать Незнайке путь? (дорожные знаки).

-Правильно, молодцы.

2. Знакомство с символами.

-А кто знает, какие знаки еще бывают?  (знаки зодиака, морские…)

-А в математике тоже есть свои знаки. Хотите узнать какие?  (да). Тогда давайте пройдем на стульчики.

Дети садятся на стульчики полукругом.

-Ребята скажите, а откуда это мы с вами можем узнать? (из газет, книг, и.т.д.) Правильно, а еще можно спросить у взрослых. Правда? (да)  И сегодня я вам расскажу о математических знаках. Они называются символы. И используются они для обозначения разных признаков. Посмотрите на 2 картинки, скажите, чем они отличаются? (размером). Правильно. А обратите внимание на условные знаки, которые показывают размер. В чем их разница? (у знака, который показывает на маленький предмет сверху 2 палочки, а на большой 4.)

-Правильно, молодцы! А теперь посмотрите на 2 листика. Чем они отличаются?  (цветом). А теперь посмотрите на символы. Чем они отличаются? (символ который указывает на цвет такого же цвета, как и лист.)

-Молодцы ребята, правильно. А теперь сравните эти 2 предмета. Найдите разницу между знаками. (указывают форму.)

-Все правильно. Молодцы!

1.3 Игра «Угадай-ка».

 -Ребята, а хотите поиграть в одну интересную математическую игру? (да). Нам нужно разделиться на 2 команды.

Дети делятся на команды и проходят к столам.

На столах лежат разложены геометрические фигуры, разных размеров и цветов.

— Сейчас я вам буду показывать символы, а вы должны будете угадать что за фигура спрятана. А я буду смотреть чья команда справится с заданием без ошибок.

Я показываю детям символы, указывающие на размер, цвет и форму, а дети должны найти среди разложенных фигур соответствующую.  Подведение итогов. Все команды молодцы, справились с заданием, победила дружба. Затем, ребенок одной из команд выходит к доске, а вторая команда показывает фигуру. Ребенок стоящий у доски должен на доске выложить символы этой фигуры ( размер, цвет, форму). Затем к доске выходит ребенок  из другой команды, а первая команда показывает геометрическую фигуру. В конце подводятся итоги.

2. Физминутка.

-Устали ребята? (да.)   ну тогда давайте отдохнем.

Дети выходят на коврик и делают разминку.

Видишь бабочка летает?

На лугу цветы считает

Раз, два, три, четыре, пять, ох никак не сосчитать.

За день, за два и за месяц, 6-7-8-9-10.

Даже мудрая пчела, сосчитать бы не смогла!

А теперь ребята встали, быстро руки вверх подняли

Наклонились в стороны, вперед, назад

Повернулись вправо, влево

Тихо сели вновь за дело!

3. Закрепление представлений о символах.

Работа в тетрадях.

-Ребята, давайте откроем рабочие тетради на странице 58, там, где лежит закладка.

1. №1 стр.58

-Ребята, посмотрите на картинки. Что на них изображено? (символы которыми обозначают погоду). Сейчас я предлагаю вам выступить в роли ведущих и рассказать нам о погоде на 5 дней. (ребенок по символам описывает погоду. Например, в понедельник солнечная, во вторник пасмурная и т.д.).

2. №2 стр. 58

-Ребята, посмотрите внимательно на следующее задание. Как вы думаете, что тут нужно сделать?  (обозначить символами размер фигур).

Дети в пустых клеточках рисуют соответствующие символы.

3. №3-4 стр. 58

-Скажите пожалуйста, а как вы думаете, что нужно сделать в следующих двух заданиях?  (это игра «Угадай-ка». Сначала нужно в клетках обозначить свойства фигур, а потом наоборот, нарисовать фигуру по указанным свойствам.)

4. № 5 стр.59

-Ребята, посмотрите на задание №5, Незнайка написал письма своим друзьям. И зашифровал их. Хотите помочь львенку и котенку расшифровать их? (да)

Дети расшифровывают записи: сначала надо нарисовать 2 маленьких треугольника, затем 1 большой круг, и 3 маленьких квадрата.  Во втором письме сначала 1 большой квадрат, 1 большой круг, и 4 маленьких треугольника.

Дети закрывают тетради, и кладут на край стола.

-хорошо, все справились с заданием. А теперь давайте мы зашифруем для Незнайки письмо на доске.

Дети встают и подходят к доске.

4. Итог занятия. Рекомендации для занятий родителей с детьми.

-Молодцы ребята! Скажите пожалуйста, что нового вы сегодня узнали? Что вам больше всего понравилось? А что вызвало затруднение?   Незнайка благодарит вас за то, что вы ему помогли. Теперь вы тоже можете зашифровать свои письма и отправить Незнайке или львенку с котенком.

МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ — ФОРМУЛЫ по МАТЕМАТИКЕ

Знак	Значение
=	равно
≡	тождественно равно
≈	приближённо равно
≠	не равно
<	меньше
>	больше
≤	меньше или равно
≥	больше или равно
+	плюс (знак сложения)
%	процент
—	минус (знак вычитания)
* или x	знаки умножения (часто опускаются: а*b = axb = ab)
m	масса
:	знак деления
аn	возведение числа а в степень n (n — показатель степени)
	знак квадратного корня (квадратный корень из числа а)
	корень n-ой степени из числа а
( ), [ ],{}	скобки (круглые, квадратные и фигурные — для обозначения последовательности действий)
┴	перпендикулярно
║	параллельно
~	подобно
∆	треугольник
‹	угол
(	дуга
0	градус
‘	минута
«	секунда
const	константа (постоянная величина)
π	отношение длины любой окружности к её диаметру
e	основание натуральных логарифмов
∞	бесконечность
f(x)	функция независимого переменного (аргумента) х
sin	синус
cos	косинус
tg	тангенс
ctg	котангенс
sec	секанс
cosec	косеканс
arcsin	арксинус
arccos	арккосинус
arctg	арктангенс
arcctg	арккотангенс
sh	синус гиперболический
ch	косинус гиперболический
th	тангенс гиперболический
cth	котангенс гиперболический
sch	секанс гиперболический
csch	косеканс гиперболический
Ig, ln	логарифмическая функция
loga	логарифм по основанию а
Igb	десятичный логарифм числа b
Inb	натуральный (по основанию е) логарифм числа b
lim	предел
	предел функции (выражения) при стремлении аргумента к величине а (а может быть ± ∞)
	сумма
	сумма последовательности членов An, где n — целое число (номер), которое может меняться от a до b (a и b — целые числа, могут быть a = — ∞, b = + ∞)
	производная функции по аргументу (переменной) х
	производная функции нескольких переменных по одному из них (частная производная)
	интеграл функции (неопределённый)
	определённый интеграл (в пределах от а до b; а и b могут быть: а = — ∞, b = + ∞)
i	мнимая единица
a + bi	запись комплексного числа w (a — действительная часть, b — мнимая часть)
R(w)	запись действительной части а
Im(w)	запись коэффициента мнимой части b
|w|	модуль комплексного числа w
	сопряжённое комплексное число ( = а -ib)
или a	обозначение вектора
|a|	модуль (длина) вектора
	единичные векторы (орты) в трёхмерной декартовой системе координат
ax, ay, az	компоненты вектора а в декартовой системе координат
	скалярное произведение двух векторов (в декартовой системе координат)
	векторное произведение векторов, в декартовой системе координат
	оператор Гамильтона («набла»)
	оператор Лапласа («дельта»)
grad	градиент скалярного поля
div	дивергенция векторного поля
n! =1•2•3•…•n	факториал — целое число (принимается, что 0! = 1)
	целая часть числа, антье

Геометрические символы

Геометрические символы Диаграмма

Давайте посмотрим на различные символы и их соответствующие значения

Геометрические символы Диаграмма

Символ	Название символа		Пример
∠	Угол	, образованный двумя лучами	∠PQR = 400
∡	20 Измеренный угол 17 между двумя углами	PQR = 70º
⊾	Угол	, образованный двумя лучами	∠PQR = 60º
∟	20 Прямой угол 17 9000 образуют угол 90º	∠PQR = 90º
º	Градус	1 поворот = 360º	∠PQR = 60º
Arcminute	1º = 60 ‘	∠PQR = 40º49 ′
“	Arcsecond	1′ = 60”	30 ”
AB	Отрезок линии	линия от точки A до точки B	Lin e AB с конечными точками A и B
\ [\ overleftrightarrow {AB} \]	Линия	бесконечная линия	Линия AB бесконечна в обоих направлениях
\ [\ overrightarrow {AB} \]	ray	Линия, начинающаяся из точки A	Линия, начинающаяся из точки A и проходящая через точку B бесконечно
⊥	перпендикуляр	перпендикулярные линии (угол 90º)	BC AB (читается как AB перпендикулярно AB)
	Не перпендикулярно	Линии не перпендикулярны друг другу	до н.э. AB (читается как BC, не перпендикулярно AB)
≅	соответствует	эквивалентность двух треугольников	∆PQR ≅ ∆XYZ R (читается как ∆PQ to ∆PQ to ∆PQ to XYZ)
∥	параллельно	параллельных прямых	AB || CD (читается как AB и CD — параллельные линии)
∦	Не параллельно	Непараллельные линии	AB CD (читается как AB и cd — непараллельные линии)
Δ	Треугольник	Форма треугольника	ΔABC ≅ ΔPQR
20 □	Четырехугольник	Форма любого четырехугольника
~	Сходство	одинаковые формы, но не одинакового размера	∆ABC ~ ∆PQR (читается как ∆ABC аналогично ∆PQR)
π	постоянная пи	π = 3.141592654… или 22/7 — отношение длины окружности к диаметру окружности	c = πd = 2πr
| x – y |	Расстояние	расстояние между точками x и y	| x – y | = 3
рад	радиан	радиан угловая единица	360 ° = 2π рад
c	радиан	радиан радиан	360 ° = 2π c
град	градуса	градуса Угловой блок	360 ° = 400 градусов
g 900 grad20	/ gons	Угловой элемент	3600 = 400g

Это очень важная таблица геометрических символов, которая поможет вам в решении проблем.Очень важно запоминать эту таблицу геометрических символов.

Еще несколько общих символов

[Изображение будет загружено в ближайшее время]

Помимо вышеупомянутых, существуют более общие символы, связанные с геометрией.

На рисунке выше изображен неправильный пятиугольник, пятиугольник.

Давайте посмотрим на некоторые используемые символы:

Углы обычно обозначаются дугой, если это острый или тупой угол, или полуквадратом, если это прямой угол. На приведенном выше рисунке отметки зеленого цвета обозначают углы

Алфавиты A, B, C, D и E — это вершины фигуры, которые могут быть отмечены любыми алфавитами.Пересечение двух прямых — вершина.

Отметки оранжевого цвета по бокам фигуры указывают на то, что две стороны совпадают. Стороны, на которых отмечен этот знак, совпадают. Отметки также называются «отметками штриховки». Например, сторона AB соответствует стороне DE. А сторона BC конгруэнтна стороне CD.

Символ углов «» чаще всего используется для обозначения любого угла. Угол ABC выражается как ABC. Средний алфавит здесь — вершина угла.Вы описываете, поэтому мы также можем записать его как ∠B. И если вы хотите записать меру угла, тогда она записывается как m∠ABC или m∠B. Вместо того, чтобы снова и снова писать слово «мера», мы можем просто написать для него слово m.

Например, нам нужно показать величину угла ABC, которую мы можем записать как

м∠ABC = 1200

Или

м∠B = 1200

При решении задач писать таким образом становится проще.

Код, скрытый в искусстве каменного века, может быть корнем человеческого письма

Элисон Джордж

Найдите знаки: геометрические формы можно найти на картинах, как в Марсуласе во Франции

Philippe Blanchot / hemis.fr / Hemis / AFP

Когда Женевьева фон Петцингер впервые увидела ожерелье, она испугалась, что поездка на полпути вокруг земного шара во французскую деревню Ле-Эзи-де-Тайак оказалась напрасной. Десятки древних оленьих зубов, лежащих перед ней, каждый из которых был проткнут, как бусинка, выглядели примерно одинаково. И только когда она перевернула один, волосы на затылке встали дыбом. На реверсе были три выгравированных символа: линия, X и еще одна линия.

Фон Петцингер, палеоантрополог из Университета Виктории в Канаде, возглавляет необычное исследование пещерного искусства.Ее интересуют не захватывающие дух изображения быков, лошадей и бизонов, которые обычно приходят в голову, а более мелкие геометрические символы, которые часто встречаются рядом с ними. Ее работа убедила ее в том, что простые формы — это не случайные каракули, а фундаментальный сдвиг в умственных способностях наших предков.

Первая известная нам формальная система письма — клинопись древнего города Урук, насчитывающая 5000 лет, на территории современного Ирака. Но она и другие подобные ей системы, такие как египетские иероглифы, сложны и возникли не на пустом месте.Наверное, раньше люди впервые начали играть с простыми абстрактными знаками. В течение многих лет фон Петцингер задавался вопросом, представляют ли круги, треугольники и волнистые линии, которые люди начали оставлять на стенах пещер 40 000 лет назад, то особое время в нашей истории — создание первого человеческого кода.

Если да, то следы не следует нюхать. Наша способность представлять концепцию абстрактным знаком — это то, чего не может сделать ни одно другое животное, даже наши ближайшие кузены шимпанзе.Возможно, это также основа нашей передовой глобальной культуры.

Первым шагом к проверке ее теории было скрупулезное документирование знаков, их местоположения, возраста и стиля, а также прослеживание появления каких-либо закономерностей. Для этого фон Петцингер пришлось бы посетить как можно больше пещер: акцент археологии на изображениях животных означал, что знаки часто упускались из виду в существующих записях.

Black tectiforms в Лас-Чименас, Испания

D v. Petzinger

Это была непростая или гламурная работа.Получить доступ к пещерам во Франции, где сосредоточено множество произведений искусства каменного века, может быть чертовски сложно. Многие из них находятся в частной собственности и иногда ревностно охраняются археологами. Чтобы получить полный набор символов, фон Петцингеру также пришлось посетить множество малоизвестных пещер, в которых нет больших ярких картин. В Эль-Портильо на севере Испании все, что ей нужно было сделать, это записка археолога, сделанная в 1979 году из каких-то «красных знаков»; с тех пор никто не вернулся. Сначала фон Петцингер даже не мог найти вход.В конце концов, она заметила крошечное отверстие на уровне колен, по которому течет вода. «Слава богу, у меня нет клаустрофобии», — говорит она. Через 2 часа скольжения по грязи внутри горы она нашла две точки, окрашенные розоватой охрой.

В период с 2013 по 2014 год фон Петцингер посетил 52 пещеры во Франции, Испании, Италии и Португалии. Символы, которые она нашла, варьировались от точек, линий, треугольников, квадратов и зигзагов до более сложных форм, таких как формы лестниц, трафареты для рук, что-то, называемое tectiform, немного напоминающее столб с крышей, и формы перьев, называемые пенниформами.В некоторых местах знаки были частью более крупных картин. В другом месте они были сами по себе, например, ряд колокольчиков, найденных в Эль-Кастильо на севере Испании (см. Рисунок ниже), или панель из 15 пенниформ в Сантиане, также в Испании.

В Эль-Кастильо в Испании: черный пенни и колокольчики

D v. Petzinger

«Наша способность представлять концепцию абстрактным символом исключительно человеческая»

Пожалуй, самым поразительным открытием стало то, как мало знаков было — всего 32 во всей Европе.На протяжении десятков тысяч лет наши предки, кажется, любопытным образом соответствовали символам, которые они использовали. Это, по крайней мере, предполагает, что маркировка имела какое-то значение. «Конечно, они что-то значат», — говорит французский доисторик Жан Клотт. «Они делали это не для развлечения». Он утверждает, что многократное повторение символа P-образной ключицы во французской пещере Нио «не может быть совпадением».

Благодаря тщательной лесозаготовке фон Петцингера теперь можно увидеть тенденции — новые вывески, появляющиеся в одном регионе, остаются на некоторое время, прежде чем выйдут из моды.Ручные трафареты, например, были довольно распространены в самые ранние периоды эпохи верхнего палеолита, начиная с 40 000 лет назад, а затем вышли из моды 20 000 лет спустя. «Вы видите, что происходят культурные изменения», — говорит фон Петцингер. Самый ранний из известных пенниформ датируется примерно 28000 лет назад в Гранд-Грот д’Арси-сюр-Кюр на севере Франции, а позже появляется немного западнее оттуда, а затем распространился на юг. В конце концов, он достигает северной Испании и даже Португалии. Фон Петцингер считает, что сначала он распространился по мере миграции людей, но его более позднее распространение предполагает, что затем он пошел по торговым путям.

Исследование также показывает, что современные люди использовали две трети этих знаков, когда они впервые поселились в Европе, что создает еще одну интригующую возможность. «Это не похоже на начальную фазу совершенно нового изобретения», — пишет фон Петцингер в своей недавно опубликованной книге Первые знаки : Раскрывая тайны старейших символов мира (Саймон и Шустер). Другими словами, когда современные люди впервые начали переселяться в Европу из Африки, они, должно быть, принесли с собой мысленный словарь символов.

Это хорошо согласуется с обнаружением 70 000-летнего блока охры с гравировкой перекрестной штриховки в пещере Бломбос в Южной Африке. И когда фон Петцингер просмотрела документы по археологии в поисках упоминаний или иллюстраций символов в наскальном искусстве за пределами Европы, она обнаружила, что многие из ее 32 знаков использовались по всему миру (см. «Последовательные рисунки»). Есть даже соблазнительные доказательства того, что более ранний человек, Homo erectus , намеренно нарисовал зигзаг на раковине на Яве около 500 000 лет назад.«Способность людей создавать систему знаков явно не зародилась 40 000 лет назад. Эта способность насчитывает как минимум 100 000 лет, — говорит Франческо д’Эррико из Университета Бордо, Франция.

Тем не менее, кажется, что в Европе ледникового периода произошло нечто особенное. В различных пещерах фон Петцингер часто находил определенные символы, используемые вместе. Например, начиная с 40 000 лет назад трафареты для рук часто находят рядом с точками. Позже, между 28 000 и 22 000 лет назад, к ним присоединились трафареты для большого пальца и рифление для пальцев — параллельные линии, образованные путем протаскивания пальцев через мягкие пещерные отложения.

Протравленные зубы

Такие комбинации особенно интересны, если вы ищете глубокие истоки систем письма. В настоящее время мы легко комбинируем буквы в слова и слова в предложения, но это сложный навык. Фон Петцингер задается вопросом, начали ли люди верхнего палеолита экспериментировать с более сложными способами кодирования информации с использованием преднамеренных повторяющихся последовательностей символов. К сожалению, это трудно сказать по знакам, нарисованным на стенах пещер, где расположение могло быть преднамеренным или совершенно случайным.«Сложно доказать, что знак был задуман как комбинация двух или более разных знаков», — говорит д’Эррико.

Протравленные зубы оленя из Сен-Жермен-де-ла-Ривьер, Франция

D v. Petzinger

Когда она решала эту загадку, фон Петцингер узнал о ожерелье из зубов благородного оленя. Он был найден среди других артефактов в могиле молодой женщины, умершей около 16000 лет назад в Сен-Жермен-де-ла-Ривьер, на юго-западе Франции.Из описания в книге фон Петцингер знал, что на многих зубах вырезаны геометрические узоры. Поэтому она поехала из Канады в Национальный музей предыстории в Ле-Эзи-де-Тайак, где находились зубы, в надежде, что они могут оказаться недостающей частью ее головоломки.

В тот момент, когда она перевернула первую, она поняла, что поездка того стоила. Х и прямые линии были символами, которые она видела вместе и по отдельности на стенах различных пещер. Теперь они были здесь, с X, зажатым между двумя строками, чтобы сформировать составной символ.Когда она переворачивала каждый зуб, открывалось все больше и больше украшений. В итоге 48 были выгравированы одиночными знаками или комбинациями, многие из которых также были найдены в пещерах. Написаны ли символы на самом деле, зависит от того, что вы подразумеваете под словом «письмо», — говорит д’Эррико. Строго говоря, полная система должна кодировать всю человеческую речь, исключая признаки каменного века. Но если вы понимаете, что это означает систему для кодирования и передачи информации, тогда можно рассматривать символы как первые шаги в развитии письма.Тем не менее, взлом доисторического кода (см. «Что они означают?») Может оказаться невозможным. «То, что мы называем квадратом для австралийского аборигена, может представлять собой колодец», — говорит Клоттс.

Что касается д’Эррико, мы никогда не поймем значение символов, не приняв во внимание также изображения животных, с которыми они так часто ассоциируются. «Совершенно очевидно, что эти два понятия имеют смысл вместе», — говорит он. Точно так же клинопись состоит из пиктограмм и счетных таблиц. Рацион, например, представлен чашей и человеческой головой, за которыми следуют линии для обозначения количества.

Фон Петцингер указывает еще на одну причину, по которой символы являются особенными. «Способность реалистично рисовать лошадь или мамонта просто впечатляет», — говорит она. «Но ведь кто угодно может нарисовать квадрат? Чтобы нарисовать эти знаки, вы не полагаетесь на людей, обладающих художественными способностями ». В некотором смысле скромный характер таких форм делает их более доступными для всех, что является важной особенностью эффективной системы связи. «Существует более широкая вероятность того, для чего они могут быть использованы и кто их использовал.”

Больше всего она считает, что изобретение первого кода представляет собой полный сдвиг в том, как наши предки делились информацией. Впервые им больше не нужно было находиться в одном месте в одно и то же время, чтобы общаться друг с другом, и информация могла пережить своих владельцев.

Квест еще далек от завершения. Фон Петцингер планирует расширить свой словарь каменного века, добавив множество знаков на переносных предметах, в пещерах на других континентах и, возможно, даже на тех, что находятся под волнами (см. «Дайвинг для искусства»).«Сейчас у нас есть только часть картины. Мы находимся на пороге захватывающего времени ».

Что они означают?

Геометрические отметки, оставленные рядом с фресками с изображением животных, десятилетиями привлекали любопытство и пристальное внимание археологов, хотя только недавно одна исследовательница, Женевьева фон Петцингер, начала систематически каталогизировать их все в доступной для поиска базе данных, чтобы попытаться определить их значение (см. история).

Для французского доисторика Анри Брейя, изучавшего наскальное искусство в начале 20 века, все картины и гравюры были посвящены охоте и магии.В абстрактных символах он видел изображения ловушек и оружия — значения, которые были неразрывно связаны с более крупными картинами. В 1960-х годах французский археолог Андре Леруа-Гуран заявил, что линии и крючки — это мужские знаки, а овалы и треугольники — женские.

Некоторая часть этой интерпретации прижилась. Круги и перевернутые треугольники до сих пор часто упоминаются в литературе как изображения вульвы. Стоит отметить, что многие из ранних ученых, изучающих пещерное искусство, были мужчинами, что, возможно, привело к гендерным предубеждениям в их интерпретациях.«Интересно, что вначале эту работу выполняли преимущественно мужчины-археологи, и повсюду было обнаружено множество вульв. Это могло быть продуктом времени, но, опять же, многие культуры действительно придают большое значение фертильности », — говорит фон Петцингер.

Позже южноафриканский археолог Дэвид Льюис-Уильямс предложил нейропсихологическую интерпретацию некоторых символов. Как и многие его сверстники, Льюис-Уильямс считает, что по крайней мере некоторые произведения искусства каменного века были созданы во время или после галлюциногенных путешествий, возможно, как часть шаманских ритуалов.Если это так, символы могут быть просто буквальными изображениями галлюцинаций. Некоторые исследования показывают, что наркотики и мигрень могут вызывать как линейные, так и спиральные паттерны, похожие на те, что наблюдаются в искусстве ледникового периода.

Но печальная правда заключается в том, что без машины времени мы, возможно, никогда не узнаем, что наши предки передавали с помощью этих знаков.

Дайвинг для искусства

Некоторые из самых потрясающих наскальных рисунков в Европе были обнаружены только в 1985 году, когда дайверы обнаружили вход в пещеру Коскер на 37 метров ниже побережья Средиземного моря недалеко от Марселя на юге Франции.Его вход был затоплен из-за повышения уровня моря после последнего ледникового периода. Скорее всего, другие подобные пещеры ждут своего открытия.

Итак, фон Петцингер объединился с Дэвидом Лангом из OpenROV в Беркли, Калифорния, который производит недорогих подводных роботов. В следующем году они планируют использовать их для поиска подводных входов в пещеры у северного побережья Испании. Этот регион богат расписными пещерами, многие из которых расположены недалеко от береговой линии, поэтому кажется вероятным, что другие могли прятаться под волнами.

Если они найдут что-либо, пара отправит дистанционно управляемые мини-подводные лодки, вооруженные камерами, для безопасного исследования новых мест.

Эта статья появилась в печати под заголовком «Скрытые символы»

Еще по этим темам:

Искусство, символы и значения сакральной геометрии — Pardesco

Сакральную геометрию часто называют «архитектурой вселенной», она встречается повсюду в мире природы.Это повсюду вокруг нас, и это один из очень немногих предметов, которые одновременно удовлетворяют и левое, и правое полушария. Он удовлетворяет желание левого полушария мозга получать логические, последовательные и объективные данные. Он также удовлетворяет потребность правого мозга в случайных, интуитивных и субъективных данных.

Просто невозможно охватить все аспекты сакральной геометрии, хотя я постараюсь включить как можно больше в эту статью. Люди потратили целые жизни на изучение одного аспекта сакральной геометрии; например, раввин, изучающий каббалистическое древо жизни.Следующее содержимое предоставляет обзор всех символов сакральной геометрии.

На рисунке ниже показаны все основные формы сакральной геометрии.

VESICA PISCIS

Vesica Piscis — математическая фигура, образованная пересечением двух одинаковых кругов так, чтобы центр каждого круга пересекал периметр другого. Vesica piscis обычно используется для диаграмм Венна, а также в различных искусствах и организациях печати.

Различные другие символы могут быть получены из vesica piscis, включая Ихтис, также известный как «Рыба Иисус», символ трикетры и треугольник Рело. Это также символ, используемый масонами на протяжении многих лет. Исторически vesica piscis использовалась как система пропорций для архитектуры, проиллюстрированная в работах Витрувия.

СЕМЕНА ЖИЗНИ

Семя жизни — универсальный символ, который также представляет семь дней творения.Он встречается во всех основных религиях и его можно увидеть во многих местах по всему миру, таких как церкви, мечети, молитвенники и древние храмы. Двумерная проекция семени жизни содержит семь перекрывающихся кругов. Он веками использовался как символ благословения и защиты.

ЯЙЦО ЖИЗНИ

Символ, который использовался для обозначения новой жизни, возрождения и плодородия. Яйцо Жизни — вторая итерация процесса конструирования Цветка Жизни.Добавив шесть дополнительных кругов к семени жизни, вы сможете произвести Яйцо Жизни. Он также может быть образован восемью сферами, содержащимися в трехмерном Кубе Метатрона.

ЦВЕТОК ЖИЗНИ

Цветок жизни был известен во всем мире в древние времена и был найден в Ирландии, Турции, Египте, Греции, Китае, Израиле, Германии, Англии, Тибете, Японии и Швеции.

Типичное изображение Цветка Жизни всегда останавливается после 19 кругов, остальные круги скрыты за пределами внешнего круга.В прошлом этот образ и знания, связанные с Цветком Жизни, были настолько священными, что они не могли допустить, чтобы они стали общеизвестными. Из полного паттерна Цветка Жизни появляется новая форма; Плод жизни.

Цветок Жизни считается действительным планом Вселенной, продолжающим основной дизайн каждой атомной и молекулярной структуры, формы жизни и т. Д .; по сути все, что существует. Современная наука и квантовая физика подтверждают космическое значение этих древних сакральных геометрических форм, которые представляют собой строительные блоки нашей физической вселенной.Древние знали об энергетической природе нашего существования. Другие священные образцы, такие как Яйцо Жизни, Семя Жизни и Древо Жизни, также существуют в образце Цветок Жизни.

ГЕРМ ЖИЗНИ

ДЕРЕВО ЖИЗНИ

Древо жизни — еще один популярный универсальный символ, представляющий многочисленные системы различных культур и религий. Как и все другие символы в этом списке, он не идентифицируется какой-либо одной культурой и использовался во всем мире на протяжении веков.

Так что же представляет собой Древо Жизни? Связь со всем, включая то, что мы не можем видеть, или пустоту за его пределами. Это напоминает вам, что вы не одиноки во Вселенной, а, скорее, являетесь частью огромной взаимосвязанной сети.

Древо жизни представляет собой иерархическую структуру для всех сил во Вселенной. Его также можно использовать как дорожную карту души. Десять сфер называются «Сефирот», что в переводе означает «возвышение». Они связаны разными путями.Первая Сефира на Древе Жизни находится наверху. Он представляет космическое сознание. Сефира в основании представляет материальный мир. Остальные Сефирот представляют разные качества Души. Их можно разделить на три столпа; Столп жестокости, столп кротости и столп милосердия.

ПЛОД ЖИЗНИ

13 сфер представляют собой чрезвычайно мощный сакральный геометрический узор, известный как Плод жизни , считающийся Святым Святых сакральной геометрии, потому что он спрятан в древнем и хорошо известном узоре Цветка Жизни.

Плод жизни состоит из 13 сфер; на самом деле это 2-е представление трехмерной структуры. Тринадцать представляет собой единство и переход между мирами / измерениями.

Те из вас, кто играет на музыкальном инструменте, знают хроматическую гамму из 12 нот: тринадцатая нота фактически повторяет первую ноту, но на более высокой частоте; когда вы достигаете более высокой октавы, вы входите в более высокое измерение. Если мы соединим все центры 13 кругов, в результате получится 78 линий, которые создают структуру, известную как куб Метатрона . Эта структура содержит все пять платоновых тел, эти трехмерные фигуры и их различные комбинации раскрывают все возможные геометрические законы, формирующие физическую реальность, которую мы переживаем.

Сферы Плода Жизни представляют женские движения или элементы творения и обеспечивают поле для 78-лучевых мужских движений творения. Геометрия Куба Метатрона лежит в основе того, что современная физика называет квантовым вакуумом или пустотой, и является фундаментальной для процесса создания на квантовом уровне.Здесь мы говорим о том, что называется нулевой точкой, жизненной силой или энергией биосилы.

КУБ МЕТАТРОНА

Одним из самых интересных аспектов сакральной геометрии является символ, известный как Куб Метатрона . Так кто такой Метатрон? Если вы исследуете, Метатрон был архангелом, который упоминался в исламской, иудейской и христианской средневековой мифологии. Он считался писцом Бога, что сделало бы его эквивалентом древнеегипетских писцов богов, известных как Тот.Согласно легенде, писец Бога понимал бы основные принципы творения, которые почти всегда связаны со священной геометрией. Много раз Архангел Метатрон изображается с кубом или держащим его.

Графика, известная как Куб Метатрона, не появлялась до тех пор, пока средневековый итальянский математик Леонардо Пизано не обнаружил Куб Метатрона. Он читал историю и легенды Метатрона, а также был знаком с сакральной геометрией и, вероятно, был посвященным в одной из школ, хранящих эти секреты.

Куб Метатрона восходит к первому узору природы и 13 кругам, которые находятся внутри четвертого круга первого узора Природы. Когда вы соединяете центры всех 13 кругов, вы получаете форму, известную как Куб Метатрона. Леонардо Пизано также обнаружил, что вы можете создать все 5 платоновых тел внутри Куба Метатрона. Куб Метатрона — это трансцендентная форма, которая прекрасно иллюстрирует ментальную вселенную через развертывание двухмерных реальностей в трехмерные реальности

Герметическая аксиома гласит: «Все есть разум, вселенная ментальна», и Куб Метатрона учит нас этой концептуальной ментальной природе вселенной, и текущие эксперименты в квантовой физике также учат нас тому же самому.Ничего не могло существовать, не будучи сначала концептуальным эквивалентом в сознании. Сакральная геометрия — это концептуальная архитектура создателя, на которой все осыпается.

СЕТКА ЖИЗНИ

Звездный тетраэдр является основой тетраэдра из 64 сеток, также известного как Решетка Жизни. Это мужской эквивалент модели Цветка Жизни. Как следует из названия, эта форма состоит из 64 тетраэдров. Как вы знаете, это одно из платоновых тел.

Когда 64-тетраэдр накладывается на цветок жизни, это представляет собой мощную концепцию; сферы представляют собой пространство, а линии-линии представляют собой место, где встречаются пространство и время.

Один из самых захватывающих аспектов тетраэдра 64 — это само число 64 и то, как оно встречается в мире природы.

Вот несколько примеров:

• В ДНК человека 64 кодона
• 64 — это количество клеток, которое у нас есть до того, как клетки начнут раздваиваться (дифференцироваться) после зачатия.
• 64 является основным числом в памяти компьютера и битами кода
• 64 закодирован в Тетраграмматоне в еврейской Библии, который представляет собой четырехбуквенный теоним ЯХВЕ, что означает Бог на иврите.
• 64 — количество поколений от Адама до Иисуса
• 64 проявления Господа Шивы в индуизме
• 64 квадрата на шахматной и шашечной досках
• 64 гексаграммы в И Цзин
• 64 тантры, являющиеся формой индуизма
• 64 — максимальное количество штрихов в любом китайском иероглифе

Этот метафизический символ может породить множество деревьев жизни, которые излучаются внутрь, поэтому 64 тетраэдра символизируют соединение индивидуальных путей в гармонии с нашей душевной семьей.Говорят, что связь со своей душой / звездной семьей усилит энергию каждого человека для достижения и воплощения своих целей. Настоящий символ главного принципа гармонии с группой людей.

ВЕКТОРНОЕ РАВНОВЕСИЕ 1

ВЕКТОРНОЕ РАВНОВЕСИЕ 2

ТОР

Форма, известная как « Torus », представляет собой тип вихря.Так что же такое тор? Слово «тор» происходит от латинского слова, означающего набухание. В сакральной геометрии это первая форма, появившаяся из Узора Бытия. Тор присутствует во всем: от атомов до форм жизни и даже во всех космических телах, таких как звезды и галактики. Это основная существующая форма.

На протяжении многих лет «провидцы» учили, что человеческая аура представляет собой серию вложенных торообразований вокруг тела. Энергия течет через центр тела и по кругу соединяет ступни и голову.Поток от ступней к голове является двунаправленным. Энергия течет через поверхность тора и внутри спиралевидного узора, поэтому форма сакральной геометрии показана с кривыми линиями по центру, а также добавляется иллюзия трехмерной перспективы к 2-му изображению.

Тор — это двухмерное изображение трехмерной формы, как и многие другие формы сакральной геометрии. Трехмерная форма известна как роговой тор. Это можно математически описать здесь.

MERKABA

Символ Меркаба (также пишется как Меркаба) переводится как свет, дух, тело.Символ состоит из двух пересекающихся тетраэдров, которые вращаются в противоположных направлениях, что создает энергетическое поле, которое обычно называют световым телом.

Мистицизм Меркавы — ранняя школа иудаизма, исповедуемая между 100 г. до н.э. — 1000 г. н.э. Учения были основаны на видениях из Книги Иезекииля и литературы хехалот. Эти истории говорят о восхождении на небеса и к Престолу Бога.

Каждый имеет доступ к своей личной Меркабе или световоду с практикой медитации.Говорят, что как только человек получает доступ к их Меркабе, она может обеспечить мощную защиту и перенести ваше сознание в более высокие измерения. Символ Меркавы может напоминать нам о потенциальной силе, которой мы обладаем, когда объединяем энергию нашего тела с Источником.

Этот символ сочетает в себе противоположные энергии в совершенной гармонии и, как утверждается, использовался вознесенными мастерами для связи с высшими сферами. В современных эзотерических учениях Меркаба считается межпространственным проводником. Он также известен как звездный тетраэдр и может быть представлен как трехмерная звезда Давида.

КАК НАРИСОВАТЬ ФОРМЫ СВЯТОЙ ГЕОМЕТРИИ

Все основные формы сакральной геометрии могут быть легко получены из этой кубической сетки, разработанной Pardesco.

Как создается сакральная геометрия?

Позвольте мне показать вам, как природа создала свой самый первый узор. Интересно отметить, что Бытие в Библии по существу описывает тот же процесс, который я собираюсь вам показать.Однако следует знать, что это знание, скорее всего, взято из древнеегипетских мистических школ и не является оригиналом Библии.

В начале была бесконечная пустота или полная пустота. Пространство без измерений и без времени.

Первое творение началось, когда природа, бог, дух или любой другой термин, который вы предпочитаете, проецировались во всех шести направлениях, начиная с единой точки .

В этом изображении не было создано ничего материального, только воображаемые линии, которые представляют чистое сознание, расширяющееся вперед, назад, влево, вправо, вверх и вниз.

Чтобы определить границы в пространстве, все, что нужно сделать, — это соединить конец каждой точки со всеми остальными точками. Прелесть этого в том, что ошибиться нельзя, это просто невозможно.

Когда все концы соединены, мы получаем так называемый октаэдр, который, если смотреть с правильной точки зрения, показывает гексаграмму, также известную как Звезда из Дэвид .

Теперь, когда границы созданы, относительное движение внутри пустоты возможно; где, как и раньше, сознанию не к чему было двигаться.

Согласно Библии, Ева якобы была создана из Ребра Адама — сравнивая эту историю со следующим этапом процесса, вы начинаете ценить идею о том, что, возможно, Библия — всего лишь экзотерическое воссоздание старой эзотерической мудрости.

Октаэдр состоит из идеально прямых линий. В сакральной геометрии прямые линии считаются мужскими, а изогнутые — женскими. На этом этапе у нас чисто мужская форма, поэтому масоны считают мужское начало порождающим принципом.

Следующий шаг в процессе включает в себя вращение октаэдра за один полный оборот вокруг каждой из осей, определенных ранее. Опять же, на этом этапе невозможно ошибиться. Конечным результатом всегда будет отслеживание параметров идеальной сферы.

Теперь у нас есть полностью женская форма. Ева была создана из Адама.

Сознание теперь имеет точку отсчета, сферическую мембрану, на которой можно повторить процесс.

Перемещение к внешнему краю сферической мембраны и создание другой идентичной сферы приводит к очень особой форме, известной как Vesica Piscis .

Эту форму дважды можно найти в человеческом теле в виде человеческого глаза за веками, а также линзы внутри глаза, которая регулирует фокус света.

Чтобы спроецировать третью сферу, мы переходим к вновь созданному пересечению между двумя исходными сферами.

После создания этой третьей сферы остается только одно правило, которое следует для завершения первого процесса; всегда перемещайтесь к самым внутренним исходным точкам, прежде чем проецировать другую сферу. Это приводит к идеальному процессу и предотвращает создание хаотического беспорядка.

После того, как семь из этих сфер были спроецированы в виде вихря, в результате мы получили Семя Жизни. Этот базовый базовый образец закладывает основу для создания материи и самой Вселенной.

Он также дает начало форме, известной как труба , Тор , если узор вращается вокруг его центральной точки. Тор — единственная существующая форма, которая может складываться сама по себе. Он также состоит из семи равных сегментов, которые можно визуально отображать с помощью семи цветов видимого спектра света.

«Семя жизни» — это не полный паттерн. Есть еще несколько шагов, которые нужно предпринять, каждый из которых открывает еще один слой и новый набор паттернов сакральной геометрии. Следуя правилу: всегда перемещайтесь к самой внутренней точке перед проецированием, мы добавляем дополнительные шесть сфер поверх существующего семени жизненного паттерна. Это называется вторым вихревым движением, если оно повторяется еще раз, возникает следующий законченный паттерн, известный как Цветок Жизни .

Этот символ встречается сегодня по всему миру, но самое раннее известное изображение было найдено в храме Осириса в Египте, выгравированное на граните с помощью процесса, неизвестного современной науке.

Если мы проделаем еще два вихревых движения, добавляя дополнительные сферы к Цветку Жизни, мы достигнем того, что известно как Плод Жизни. Теперь это полный шаблон для всех материальных вещей.

Древо жизни может быть получено из семени жизненного образца. Это наиболее широко признанное мистическое понятие в каббале, а также в различных мировых философиях и теологиях. В каббале он используется как инструмент для понимания природы бога и того, как мир был создан из ничего.Детали этого слишком сложны, чтобы рассказывать о них в этом руководстве.

Следующая форма известна как Яйцо Жизни, созданное из восьми сфер. Мы не видим восьмую сферу, которая находится за центральной сферой. Этот паттерн — наиболее сбалансированная и оптимизированная форма для существования восьми сфер. Причина, по которой его называют яйцом жизни, заключается в том, что природа использует эту форму в эмбриональном создании каждого живого организма на планете без исключения.

Теперь мы переходим к одному из наиболее важных наборов экстраполяций, которые могут продемонстрировать красоту сакральной геометрии как визуально, так и математически.Если мы возьмем плод жизни и извлечем тринадцать кругов, то получим куб Метатрона . Всего в трехмерной версии Куба Метатрона шестнадцать сфер.

Интересно отметить, что все параметры гиперкуба, также известного как тессеракт , можно легко извлечь из куба Метатрона. Следует также отметить, что Куб Метатрона также глубоко связан с платоновыми телами . Ниже представлена ​​двухмерная проекция тессеракта:

.

Многие древние традиции были увлечены наукой о простых трехмерных геометрических формах, которые были первоначально открыты Платоном (который изобрел школу). Платоновы тела обладают большей симметрией, чем любая другая форма, которую вы могли бы создать.

Самые продвинутые гиперпространственные модели, которые ученые пытаются построить многомерными во Вселенной. Вы можете видеть, что Платоновы Тела часто появляются, потому что они знают, что для построения более высоких измерений вам нужна большая симметрия.

ПЛАТОНИЧЕСКИЕ ТВЕРДЫЕ

В исходной модели, которую придумал Платон, каждая форма представляет собой элемент.Куб представляет Землю, Тетраэдр представляет Огонь, Октаэдр представляет Воздух, Икосаэдр представляет Воду, а Додекаэдр представляет Эфир.

Соединение ребер четырех равносторонних треугольников создает тетраэдр. Соединение граней квадратов размера создает шестигранник. Соединение ребер восьми равносторонних треугольников создает октаэдр. Соединение ребер 12 пятиугольников создает додекаэдр. Соединяя края 20 равносторонних треугольников, получается икосаэдр.Об этом он писал в своих философских текстах.

Есть пять платоновых тел: тетраэдр, октаэдр, шестигранник, икосаэдр и додекаэдр. Что делает эти формы такими особенными, так это то, что грани, углы и края совпадают, и каждая из них может идеально вписаться в сферу со всеми соприкасающимися углами. Не существует других форм, удовлетворяющих этим параметрам.

Пять платоновых тел также образуют пары, известные как драгоценности; шестигранник и октаэдр составляют пару, а икосаэдр и додекаэдр составляют другую.Тетраэдр является необычным, поскольку он представляет собой драгоценный камень сам по себе, соединяя середины каждой грани. Каждое платоновое твердое тело также связано с элементом.

ЗОЛОТАЯ СПИРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ И ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОННАЧИ

Последовательность Фибоначчи, тесно связанная с золотым сечением. Впервые он был описан математиками в Индии примерно в 700 году нашей эры и представлен на западе Леонардо Пизанским, также известным как Фибоначчи. В своей книге Liber Abaci. Проще всего найти эту последовательность в природе — это растения.Независимо от того, на какой цветок вы посмотрите, вы увидите, что количество педалей равно одному из чисел в ряду Фибоначчи. Ряды семян подсолнечника и сосновых шишек всегда в сумме дают числа Фибоначчи. Узнайте больше о последовательности Фибоначчи и ее связи с Фи здесь.

Золотое сечение. Что такое фи?

Золотое сечение встречается в древнегреческой архитектуре и некоторых известных произведениях искусства. Он встречается в природе в различных формах и, вероятно, был определен количественно после рассмотрения правильного пятиугольника с длиной стороны 1.Длина диагонали, соединяющей две смежные стороны пятиугольника, является золотым сечением. Тесно связана форма, известная как пентаграмма, если самая короткая из этих длин равна 1, то остальные длины являются степенями Фи.

Много лет назад мыслитель эпохи Возрождения Лука Пачоли был очарован этим соотношением и написал книгу под названием «Божественная пропорция», которую проиллюстрировал Леонардо да Винчи. В книге исследуются различные геометрические тела и их появление в архитектуре и человеческом теле.Многие художники во все времена использовали это соотношение в своих работах, например, Сальвадор Дали, написавший «Таинство Тайной вечери» на холсте в форме золотого прямоугольника. Другой пример — древнегреческий скульптор Фидий, который использовал золотое сечение, чтобы проиллюстрировать идею физического совершенства.

Золотой прямоугольник можно постепенно разбить на квадраты, длина сторон которых зависит от Фи. Это часто изображают с помощью Золотой спирали, соединяющей углы каждого из этих квадратов.

Три золотых прямоугольника можно создать, соединив двенадцать вершин икосаэдра. Вы можете узнать больше о математических свойствах золотого сечения здесь.

Дополнительные ресурсы:

Сакральная геометрия вики

Троицкий узел Значение

Vesica Piscis Wiki

Ichthys Символ Пояснение

Значение куба Метатрона

Гиперкуб Вики

Что загадочные символы, созданные древними людьми, могут рассказать нам о нашем развитии |

Изучив десятки пещер ледникового периода по всей Европе, палеоархеолог Женевьева фон Петцингер обнаружила, что наши предки неоднократно использовали 32 знака.Почему? Она рассказывает нам о своих открывающих глаза открытиях и их последствиях.

Титул старейшего датированного наскального искусства в мире в настоящее время носит скромный красный диск возрастом не менее 41 000 лет, нарисованный на стене внутри скального образования в Эль-Кастильо, Испания. «Он размером с блюдце для чашки», — говорит палеоархеолог Женевьева фон Петцингер (TED Talk: Почему эти 32 символа найдены в древних пещерах по всей Европе?). «Это очень безобидная мелочь».

На протяжении веков в центре внимания палеоантропологии (и народного воображения) было изобразительное искусство, которое наши предки оставили в пещерах: привлекательные рисунки оленей, лошадей, бизонов и человеческих фигур.Но когда она училась на старших курсах колледжа, фон Петцингер, научный сотрудник TED и исследователь из Университета Виктории в Канаде, обратила внимание на абстрактные знаки, на которые часто не обращают внимания: диски, треугольники, точки, круги и линии. «В них было что-то гораздо более интересное, чем животные и люди», — говорит она. «Это тоже неплохо, но казалось, что там были какие-то закономерности, и все же не было даже достаточно информации, чтобы даже вникнуть в это».

Пять лет назад фон Петцингер задумал задокументировать и систематизировать геометрические знаки, которые были созданы десятки тысяч лет назад в Европе во время ледникового периода.Она начала с составления базы данных геометрических знаков, найденных на почти 370 известных памятниках наскального искусства по всему континенту. Оттуда она выявила пробелы в инвентарях на многих объектах и, исследуя редко задокументированные места — вместе со своим мужем, фотографом / режиссером Диллоном фон Петцингером, чтобы запечатлеть изображения — она ​​сделала открытия, которые содержат дразнящие выводы о происхождении искусства и эволюция человеческого познания.

Пещера Лас-Чименас на севере Испании. Здесь изображен испанский знак tectiform (слева), местная версия знака tectiform (что означает «в форме крыши»).Испанский тектиформ является коренным для северной Испании, и предполагается, что он представляет собой изображение палеолитического жилища или лодки или является более абстрактной интерпретацией местного клана или племенного знака.

Хотя они и занимались наскальным искусством, ранние люди не совсем были «пещерными людьми». Homo sapiens — современные люди, анатомически идентичные нам сегодня — впервые появились 200 000 лет назад в Африке. Ранние люди, вероятно, не жили в пещерах, скорее, у входов в пещеры.«Пещеры были почти как их задний двор, — говорит фон Петцингер. И хотя мы в основном знаем их по рисункам на стенах пещер, начало Homo sapiens , вероятно, украшало все их окрестности. «Пещеры, вероятно, являются частью того, что раньше украшали», — говорит она. Пещерное искусство сохранилось, потому что оно было защищено от непогоды — предлагая палеоантропологам уникальный и хорошо сохранившийся взгляд на работы наших предков.

Как узнать возраст рисунка в пещере? Фон Петцингер изучает искусство, созданное 10 000–40 000 лет назад, в период верхнего палеолита ледникового периода.(Последний ледниковый период охватил примерно от 110 000 лет назад до 10 000 лет назад.) Основными методами, используемыми палеоархеологами для определения датировки наскального искусства этого периода времени, являются датирование по углеродному 14 и урановым сериям. Датирование по углероду-14 позволяет определить возраст разлагающихся органических веществ, таких как кости и краски на угольной основе, которым до 40 000 лет. Он работает, измеряя соотношение радиоактивного углерода-14, который распадается, к углероду-12, которое остается постоянным даже после того, как органическое вещество умирает. Датирование по урановым сериям — более недавнее дополнение к набору инструментов для датирования, и оно позволяет находить даты, которые восходят еще глубже.Датирование урана работает в пещерах, содержащих кальцит, минерал, который часто встречается в сталактитах и ​​других элементах живых, растущих пещер. Кальцит, переносимый каплями воды по стене пещеры, иногда может образовывать гладкий полупрозрачный слой над более ранними наскальными рисунками. Кальцит содержит уран, который со временем распадается — это означает, что если кальцит есть на стене пещеры над наскальной росписью, этот распад урана можно измерить, чтобы установить минимальный возраст произведения наскального искусства или дату, когда кальцит впервые покрыл это.«Датирование урана — вот источник многих этих захватывающих новых открытий, — говорит фон Петцингер, — потому что он открыл целый мир гравюр и типов картин, которые мы не могли датировать раньше».

Вверх по боковому проходу от главной дороги в пещере Эль-Кастильо в Испании вы найдете единственную панель, состоящую из вывески в форме пенни (названной в честь латинского слова «перо») черного цвета, окруженной пятью красными знаками в форме колокола. . Выступ, обрамляющий нижнюю часть этой картины, придает ей почти алтарный вид.

Как найти общие знаки, соединяющие десятки пещер и 30 000 лет проживания людей. За семь месяцев в 2013 и 2014 годах фон Петцингер и ее муж посетили и задокументировали 52 пещерных места в Испании, Португалии, Франции и Италии. Она выбрала участки, на которых исследователи заметили геометрические знаки, но не зафиксировали детали. После завершения полевых исследований она проанализировала все каталогизированные знаки. И то, что она увидела, заставило волосы на затылке встать дыбом: через 30 000 лет и на всем европейском континенте всего 32 знака повторялись снова и снова.Как она могла объяснить эту преемственность? «Это действительно небольшое число говорит о том, что они, должно быть, были значимыми для людей, которые их использовали, потому что они копировали их», — говорит она.

Испанский тектиформный знак, точки и лошадь, найденные в Ла-Пасейге, Испания, богато украшенная пещера с гравюрами, рисунками животных и более 100 геометрических изображений. Учитывая стилистически разнообразное наскальное искусство Ла-Пасьеги, вполне вероятно, что различные группы посещали пещеру на протяжении сотен лет.

Эти открытия перевернули традиционную хронологию жизни человека и искусства. Палеоантропологи давно считали, что искусство было изобретено во время «творческого взрыва» 40 000 лет назад в Европе. Считается, что первые Homo sapiens мигрировали туда из Африки во время потепления ледникового периода примерно 45 000 лет назад. Но исследования фон Петцингера бросают вызов этой расхожей точке зрения. «Я поняла, что две трети знаков уже использовались, когда люди прибыли в Европу», — говорит она, предполагая, что символы являются продолжением существующей традиции, а не началом чего-то нового.Это радикально сдвигает правдоподобную временную шкалу назад, когда человечество начало создавать и использовать символы. «Некоторые из этих знаков потенциально могут быть частью более крупной системы, которую они принесли с собой, когда покинули Африку, — говорит фон Петцингер, — а затем перемещались вместе с ними по мере распространения по миру».

32 знака, которые фон Петцингер внес в каталог пещерного искусства ледникового периода по всей Европе. На их долю приходится подавляющее большинство нефигуративных образов, обнаруженных по всему континенту за этот 30 000-летний период времени, что позволяет предположить, что они использовались целенаправленно и имели значение для их создателей.Каждый из 32 знаков имеет свой собственный характер использования. Предоставлено Женевьев фон Петцингер.

Может ли отметка означать «Я был здесь»? Когда-то считавшиеся орнаментальными и представлявшими второстепенный интерес, геометрические знаки превосходили численностью репрезентативных изображений в пещерах как минимум два к одному. 32 знака, задокументированные фон Петцингером, включают точки, звездочки, спирали и отрицательные стрелки. Негативные руки или негативное изображение отпечатка руки — один из древнейших знаков, появляющихся в пещерах, и они были наиболее популярны в начале ледникового периода (между 22 000 и 40 000 лет назад).«Они могли быть сигналом того, что конкретный человек был на месте, или символическим изображением человека или группы людей», — говорит фон Петцингер. «Возможно, они даже были своего рода ранним языком жестов». Пенниформ, названный в честь латинского термина, означающего «перо» или «плюмаж», был более поздним художественным изобретением, впервые появившимся между 28 000 и 30 000 лет назад, и, возможно, использовался для изображения оружия, деревьев и растений. Tectiforms, названные от латинского слова, означающего «форма крыши», появились только между 13000 и 17000 лет назад и были обнаружены только в девяти пещерах, что указывает на то, что это, вероятно, локализованное изобретение и, возможно, даже признак клана или маркер определенной группы. личность.

Зал с испанскими тектиформами из красной охры, найденный в Эль-Кастильо. Знаки тектиформ большие — многие из них от двух до трех футов в длину. Большие группы красных точек в виде рядов или круговых узоров, кажется, чаще всего появляются на севере Испании.

художников ледникового периода обожали красный цвет. Фон Петцингер наблюдал замечательные попытки первых людей контролировать цвета своих творений, и они продемонстрировали сильное предпочтение красной охры (сделанной из оксида железа).«Иногда они использовали довольно сложные системы термообработки, чтобы нагреть охру до этих очень определенных температурных диапазонов, что вызывает химические изменения и делает ее действительно ярко-красной», — говорит она. «Мы почти видим, как они строят с огнем». Предки Homo виды начали использовать охру более 250 000 лет назад, вероятно, для практических целей — для дубления и обработки шкур животных или для отпугивания насекомых. «Вы задаетесь вопросом, могло ли каким-то образом практическое и приземленное могло быть их отправной точкой, но со временем вы начинаете видеть, что они принимают решения, основанные больше на том, что им нравится, а не на том, что было самым простым или наиболее практичным решением», — фон Петцингер. говорит.Это свидетельство предпочтения цвета также может быть признаком развития сложных символических когнитивных процессов в мозгу человека.

Неандертальцы тоже были художниками? Еще один вопрос, на который фон Петцингер надеется когда-нибудь ответить, заключается в том, наносили ли графические знаки неандертальцы — коренные жители Европы, которые жили там до своего исчезновения примерно 30 000 лет назад. Традиционно все искусство ледникового периода ученые приписывали нашим человеческим предкам.Тем не менее, недавно обнаруженная гравировка с перекрестием из пещеры в Гибралтаре, по-видимому, была сделана неандертальцами, что повышает интригующую возможность того, что этот близкородственный вид создавал искусство. «Поскольку два вида пересекались в Европе на протяжении как минимум 10 000 лет, возможно, что некоторые из знаков, датируемых 30 000 лет или старше, были сделаны неандертальцами вместо Homo sapiens , что добавило бы совершенно новое измерение в изучение льда. Возрастное искусство », — говорит фон Петцингер.

«Надпись Ла Пасьеги» — замечательная серия соединенных вместе знаков — большая редкость в искусстве ледникового периода.Хотя это не «письмо», как мы его знаем сегодня, возможно, это очень ранняя попытка создать более сложное сообщение с использованием нескольких знаков.

Связанные символы могут быть предшественниками более сложной коммуникации. Заманчиво искать алфавит или глоссарий в знаках фон Петцингера, но только 5000 лет назад люди начали разрабатывать сложные системы графической коммуникации. Тем не менее, 32 знака, похоже, обладают коммуникативными свойствами, и фон Петцингер предполагает, что мы можем проследить происхождение наших первых систем письма до этих древних символов.Возьмем, к примеру, надпись «Ла Пасьега» на севере Испании, возраст которой составляет примерно 16 000 лет, и на которой изображено несколько соединенных вместе знаков. «Хотя подобный сериал был в высшей степени необычным,« Надпись Ла Пасьеги »могла бы быть очень ранней попыткой создать более сложное послание», — объясняет она. «Люди начали экспериментировать, что, возможно, помогло привести к предложениям и написанию письма позже».

Негативная рука, один из древнейших типов образов в мире, найденный в Эль-Кастильо.Негативные руки часто делались с использованием техники рисования плевком, когда кто-то клал руку на стену пещеры и «плюнул» краской на руку и вокруг нее, оставляя контур.

Что искусство может рассказать нам об эволюции человеческого познания? «Искусство — это действительно интересное окно в сознание, — говорит фон Петцингер, — это очень абстрактная, когнитивно сложная вещь, которую нужно делать». Если бы первые люди создавали знаки с определенным значением во время ледникового периода, это означало бы огромный шаг вперед, когда мы разработали сложные системы письма.В конце концов, наша способность к графическому общению — одна из вещей, которая отличает нас от остального животного царства. «Как только вы сможете хранить информацию за пределами отдельного человека, подумайте о том, каков потенциал, чтобы иметь возможность передавать эту информацию большим группам людей и сохранять важную информацию», — говорит фон Петцингер. «Я думаю, что эти самые первые маленькие шаги на самом деле помогли нам встать на этот невероятный путь, на котором мы закончили». В настоящее время она работает над расширением своей базы данных, чтобы включить в нее сайты на Балканах и Кавказе, прежде чем расширяться дальше на восток в Евразию.Весной 2018 года она планирует отправиться в экспедицию на побережье Испании и поискать подводные пещеры, в которых, возможно, сохранились изображения ледникового периода. Это сотрудничество с предпринимателем, занимающимся подводными роботами, и товарищем по TED Дэвидом Лэнгом (TED Talk: Мой подводный робот).

Для получения дополнительной информации о работе фон Петцингер прочтите ее книгу 2016 года Первые знаки: раскрывая тайны древнейших символов мира .

Все фотографии любезно предоставлены Диллоном фон Петцингером.

геометрических символов | Justfreetools

Геометрия и тригонометрия — это разделы математики, связанные с геометрическими фигурами и углами треугольников. В следующем списке представлены некоторые из наиболее примечательных символов в этих темах, а также их использование и значение.

Для удобства чтения эти символы сгруппированы по функциям в таблицах. Другие исчерпывающие списки математических символов, сгруппированные по предмету и типу, также можно найти на соответствующих страницах ниже (или на панели навигации).

В геометрии точки и линии составляют основу более сложных геометрических фигур, таких как треугольники, окружности, четырехугольники и многоугольники. В следующей таблице приведены некоторые из наиболее примечательных символов, связанных с ними, а также их значение и пример.

---

В настоящее время у нас есть около 1975 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.

На этой странице вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитования и лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и ​​инструментах (как писать смайлы в Интернете и т. Д.)

В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.

Ниже приведены наиболее часто используемые пользователями во всем мире.

И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.

Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите хотя бы малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.

сакральных геометрических узоров, которые сделают вас единым целым с миром

сакральная геометрия | © Culture Trip / Michaela Pointon

Священные геометрические узоры существуют вокруг нас — это идеальные формы и узоры, образующие фундаментальные шаблоны жизни во Вселенной. От последовательности Фибоначчи до золотого сечения шаблоны проектирования можно разделить на язык чисел (математика), которые управляют всем нашим видимым и невидимым миром.Но каков духовный смысл этих геометрических узоров и символов?

Галилей однажды сказал: «Математика — это алфавит, которым Бог написал вселенную». Художники, музыканты и философы уже давно проявляют силу сакральной геометрии в своих работах, от да Винчи до Пифагора. Вполне вероятно, что Моцарт использовал золотое сечение в своих музыкальных произведениях. Священная спираль (последовательность Фибоначчи), например, присуща всему: от простой сосновой шишки до раковины улитки, человеческого тела и Великих пирамид в Гизе.Говорят, что твердые тела Платона (платоновые формы) составляют основу любого дизайна во Вселенной, вплоть до молекулярного масштаба.

Но священные формы также представляют нематериальные, мистические элементы жизни. Почему еще нас так тянет к ним? Коррелирует ли сакральная геометрия с чем-то более глубоким в нашем универсальном сознании? Отражает ли он язык души или говорит на нем? Или наш мозг просто запрограммирован на распознавание этих закономерностей в природе?

Какой бы ни была причина распространения этих узоров, ясно одно: символы обладают силой.Вот набор геометрических узоров, которые помогут связать ваше тело и дух со священным языком Вселенной.

Цветок жизни | © Culture Trip / Michaela Pointon

Цветок жизни, один из самых древних символов в мире, олицетворяет божественный математический порядок во всей жизни. Состоящий из равномерно расположенных, перекрывающихся кругов (с шестикратной симметрией, такой как шестиугольник), некоторые считают, что этот символ является божественным визуальным выражением жизни, сознания и творения.Леонардо да Винчи особенно интересовался формой и математическими пропорциями Цветка Жизни и его связью с физическим пространством и человеческим сознанием. Символ был найден в Храме Осириса в Абидосе, Египет, Запретном городе, Пекине, Китае, и многих других священных местах по всему миру.

Внутри символа Цветка Жизни находится изображение Семени Жизни, которое кажется очень подходящим, потому что все цветы содержат семена. Полагают, что многоугольники олицетворяют женское начало, и некоторые считают, что это символ творения (7 кругов, 7 дней, 7 чакр, 7 музыкальных нот).Эти гармоничные, взаимосвязанные круги также считаются Планом Вселенной, а также иллюстрируют митоз (или оплодотворение яйцеклетки и удвоение клеток).

Хамса | © Culture Trip / Michaela Pointon

Символ Хамса, который в основном встречается на Ближнем Востоке и в Африке, символизирует Длань Бога и, как говорят, приносит удачу и защиту владельцу. Также известный как Хамса, Хамса является священным как в исламских, так и в еврейских традициях, а первое использование символа относится к 1550–330 годам до нашей эры.Говорят, что глаз в центре руки защищает от зла.

Древо жизни | © Culture Trip / Michaela Pointon

Священные изображения деревьев существуют на протяжении веков и широко используются в большинстве мировых религий, включая иудаизм и буддизм. Этот геометрический символ находится в центре мистической традиции каббалы, но он также появился в Древнем Египте более 3000 лет назад. Хотя его корни довольно эзотерические, пространственное формирование символа должно быть вам хорошо знакомо.Национальная аллея в Вашингтоне, округ Колумбия, например, даже построена именно в такой форме. Считается, что Древо Жизни изображает божественное единство человека со Вселенной и может пониматься как карта человеческого разума или психики.

Vesica Pisces | © Культурная поездка / Микаэла Пойнтон

Три круга, составляющие Троицу Глаза Рыб, также являются частью символа Весики Рыб. Его можно понимать как представитель различных лунных циклов: растущего, полного и убывающего. Священный в различных неоязыческих традициях и традициях богини, Троица Глаза Рыб — мощный древний символ, изображающий священную троицу и всевидящее око.

Куб Метатрона | © Culture Trip / Michaela Pointon

Куб Метатрона также считается символом сотворения самой жизни; сферы представляют женское начало, а прямые линии, соединяющие их, представляют мужское начало, поскольку они работают вместе, чтобы создать единое целое. Этот могущественный символ содержит 5 Платоновых тел или 5 элементов (Земля, Воздух, Огонь, Вода и Эфир), и считается, что медитация на Куб Метатрона имеет глубокие целительные силы.

Вы, наверное, знакомы с этой формой еще в начальной школе.(Помните диаграмму Венна?) Но сакральный геометрический смысл, стоящий за ней, совершенно отличается от простого анализа сходств и различий. Перекрывающиеся круги представляют двойственность в единстве или связь между духовным миром и физическим. В центре символа Vesica Pisces вы заметите рыбу (название буквально переводится с латыни как «рыбный пузырь»), которая была принята и считалась священной ранними христианами как символ Иисуса Христа. Этот символ можно найти в церквях по всему миру.

Также известный как «Узел Вечности», тибетский узел является символом силы в тибетском буддизме и олицетворяет вечность, целостность и взаимосвязь всей жизни. Являясь частью «восьми благоприятных символов» в буддизме, вариация этого древнего символа также встречается в других культурах, таких как кельтский узел.

Буддийский символ Уналоме | © bc21 / Shutterstock

Символ Уналоме содержит священный цветок лотоса, символизирующий наше восхождение от земной борьбы к просветлению.Как буддийский символ, он также представляет третий глаз Шивы, а спиральные линии обозначают колеблющийся путь, который нужно пройти, чтобы найти истину и равновесие.

Икосамедрон, являясь пятой платонической формой, представляет собой элемент воды и связан с эмоциональной, сексуальной и творческой энергиями. Форма состоит из 20 равносторонних треугольников, и, поскольку треугольники часто ассоциируются с женской энергией, считается, что этот символ способствует плодородию и исцелению.

Символ Шри Янтры, состоящий из девяти взаимосвязанных треугольников, является мистическим символом, связанным с индуизмом.Представляя как мужскую, так и женскую энергии треугольниками, направленными вниз и вверх, символ в целом представляет собой путь человека к просветлению.

Пятиконечная звезда, или Пентаграмма, возникла тысячи лет назад, и ее можно увидеть в различных культурах и религиях, но сегодня она обычно ассоциируется с Виккой. Пять точек могут представлять пять чувств, пять ран Христа, пять платоновых тел или даже человеческое тело (как в «Витрувианском человеке» Да Винчи).

Гексаграмма | © Culture Trip / Michaela Pointon

Шестиконечная звезда, или то, что обычно называют Звездой Давида, веками использовалась в священных традициях, даже со времен царя Соломона в Ветхом Завете.Символизируя идеальное медитативное состояние в индуизме и магические церемонии в оккультных практиках, гексаграмма может вписываться в идеальный круг и часто ассоциируется с сердечной чакрой.

Геометрические знаки — типы знаков, присутствующие в странах и регионах

Типы знаков, присутствующие в странах и регионах

По сравнению с теми, что были найдены во Франции в период верхнего палеолита
Женевьев фон Петцингер

Поскольку создание наскальных изображений является постоянной практикой во многих регионах мира, включая Австралию, Африку и Северную Америку, я сосредоточился на древнейшее искусство, которое, как считается, было создано либо во время, либо вскоре после верхнего палеолита.Датировка для большинства памятников далеко не точна, поэтому некоторые могут относиться к эпохе железного века. Если наскальное искусство выполнено гравировкой или красной краской, очень сложно определить временной период, так как не на чем использовать датировку C14. Хотя в некоторых из этих случаев используются и другие методы датирования, многие из этих методов вызывают больше споров, и споры продолжаются.

В местах, где люди продолжают создавать наскальные рисунки, изучение мест, как прошлых, так и настоящих, может быть затруднено, поскольку эта практика часто имеет религиозный подтекст.Результатом может быть понятное нежелание разрешать доступ посторонним к сайтам, а это означает, что разнообразие мотивов может быть намного больше, чем известно в настоящее время.

Этот обзор нефигуративных наскальных изображений за пределами французского региона следует рассматривать только как предварительный. Я включил только те типы знаков, которые мне были знакомы или которые мне удалось визуально подтвердить, что означает, что я вполне мог случайно пропустить геометрические формы, присутствующие в некоторых из этих мест.В следующем разделе содержатся сделанные мной заметки о различных аспектах этого обзора (часто включая исходный материал). Ниже приведена диаграмма, в которой указано как можно больше стран / регионов, имеющих геометрические знаки, и указано, какие из них присутствуют.

Негативные руки
Знак этого типа встречается почти во всех регионах мира. Чтобы получить отличный обзор этого явления и увидеть несколько красивых картинок, посетите URL-адрес статьи Bradshaw Foundation по этой теме.

Европа
Большая часть информации о геометрических знаках на испанских сайтах исходит из работ Андре Леруа-Гурана. Большая часть информации, которую я нашел для других стран, поступает с отличной онлайн-базы данных (спонсируемой ЕС) под названием «Europreart». Он содержит списки многих мест наскального искусства в Западной Европе, включая изображения, и его стоит изучить: www.europreart.net

Джорджия
Есть упоминания о «символах древнего наскального искусства», присутствующих в этой стране, но Я не нашел ни одной разбивки по типу знака.Это определенно будет областью дальнейших исследований для моей докторской степени.

Индия
Хотя до сих пор продолжаются споры о возрасте этого искусства и о том, действительно ли оно относится к верхнему палеолиту, считается, что некоторые из них датируются концом этого времени (около 10 000 лет назад). . Информация о том, какие геометрические знаки присутствуют на этих сайтах (я включил только те, которые относятся к самому древнему периоду времени), взята из статьи доктора Джин Клоттес, найденной на веб-сайте Фонда Брэдшоу по следующему адресу: www.bradshawfoundation.com/india/index.html

Borneo
Некоторая информация для этой страны взята из статьи о негативных руках Фонда Брэдшоу (см. выше) и статьи National Geographic: http://ngm.nationalgeographic.com/ features / world / asia / indonesia / cave-art-text

Мьянма и Малайзия
Информация о наскальном искусстве в этих странах в настоящее время крайне ограничена, в основном из-за нехватки средств для исследований в этих странах.Теперь это может измениться, и отличный обзор этого и других наскальных рисунков из Азии / Южного Тихого океана доступен по следующему URL-адресу: http://13congresoantropologia.uniandes.edu.co/_documentos/Illustrating the Past.pdf

Africa
Там было достаточно информации, чтобы я мог несколько различать регионы, когда дело доходило до наличия геометрических знаков, хотя я бы сказал, что то, что я смог идентифицировать, далеко не полный список — так что, пожалуйста, имейте это в виду! Африканские регионы, которые я использовал в качестве категорий, следующие: Западная Центральная Африка: Габон, Камерун, Центральноафриканская Республика, Конго. Восточная Африка: Танзания. Северная Африка: Алжир, Ливия, Нигер, Чад, Южная Африка: Намибия, Южная Африка, Мозамбик, Зимбабве .

Большая часть информации об этом континенте была получена из книги доктора Дэвида Льюиса-Уильямса «Разум в пещере» и опубликованных им журнальных статей (он исследователь из Южной Африки, который провел много исследований по некоторые типы геометрических знаков как часть его работы по шаманизму). Кроме того, я взял информацию с веб-сайта Фонда Брэдшоу, на котором есть целый раздел, посвященный африканскому наскальному искусству.Еще один отличный источник материалов по Африке — «Фонд африканского наскального искусства» (TARA).

Южная Америка
Вероятно, гораздо больше стран и типов знаков, чем я включил, но исследования в этом регионе во многих случаях были ограничены из-за отсутствия финансирования. Я включил знаки, если смог найти список или наглядное изображение, так что вполне могло быть больше, чем я объяснил. Кроме того, в этом регионе не так много дат, поэтому большая часть искусства, вероятно, относится к более позднему периоду, чем верхний палеолит.Включены страны: Боливия, Аргентина и Бразилия. Информация о геометрических знаках в Боливии поступает от Фонда Брэдшоу: www.bradshawfoundation.com/bolivia/index.php

Женевьев фон Петцингер | Введение
Что такое геометрические знаки? | Всемирная таблица геометрических знаков
Методология исследования
Геометрические знаки во Франции | Страница | 1 | 2 |
Типы знаков, присутствующие в странах и регионах
Библиография
Библиография | для фотографий и рисунков | от A до L | от N до Z |

.

No related posts.