Х среднее символ: X с чертой наверху символ

X с чертой наверху символ

Помимо использования разных видов форматирования текста таких как: изменение шрифта, применение полужирного или курсивного начертания, иногда необходимо сделать верхнее подчеркивание в Ворде. Расположить черту над буквой довольно просто, рассмотрим несколько способов решения данной задачи.

С помощью «Диакритических знаков»

Благодаря панели символов сделать черточку сверху можно следующим образом. Установите курсор мыши в нужном месте по тексту. Перейдите во вкладку «Вставка» далее найдите и нажмите в области «Символы» на кнопку «Формула» и выберите из выпадающего меню «Вставить новую формулу».

Откроется дополнительная вкладка «Работа с формулами» или «Конструктор». Из представленных вариантов в области «Структуры» выберите «Диакритические знаки» и кликните по окну с названием «Черта».

В добавленном окне напечатайте необходимое слово или букву.

В результате получится такой вид.

Подчеркивание сверху посредством фигуры

Используя фигуры в Ворде, можно подчеркнуть слово как сверху, так и снизу.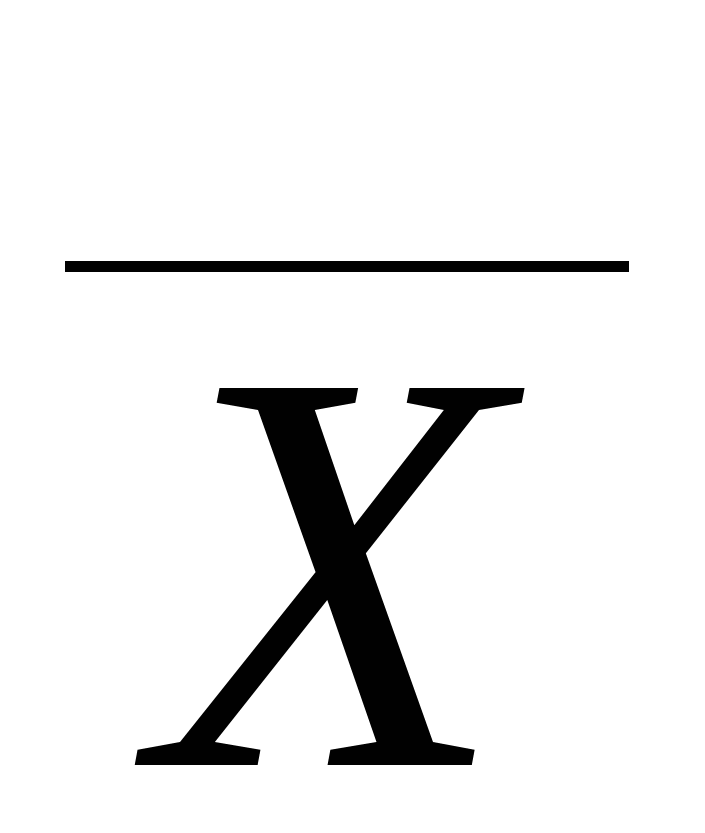

Рассмотрим верхнее подчеркивание. Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия».

Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.

Можно изменить цвет верхнего подчеркивания, нужно нажать по линии и открыть вкладку «Формат». Нажав по кнопке «Контур фигуры» указать нужный цвет. Также можно изменить вид подчеркивания и толщину. Для этого перейдите в подпункт ниже «Толщина» или «Штрихи».

В соответствии с настройками палочку можно преобразовать в штрихпунктирную линию, либо изменить на стрелку, в нужном направлении.

Благодаря таким простым вариантам, поставить черту над буквой или цифрой не займёт много времени. Стоит лишь выбрать наиболее подходящий способ из вышепредставленных.

Сре́днее арифмети́ческое (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённой на их количество.

Является одной из наиболее распространённых мер центральной тенденции.

Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).

При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.

Содержание

Введение [ править | править код ]

Обозначим множество чисел X = (x₁, x₂, …, x_n), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ <displaystyle <ar >> , произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки x_i

из этой совокупности μ = E<x_i> есть математическое ожидание этой выборки. x_=<frac <1>>(x_<1>+cdots +x_).>

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше

n, тем меньше различие между новым и старым средними значениями.

Примеры [ править | править код ]

• Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:

x 1 + x 2 + x 3 3 . <displaystyle <frac +x_<2>+x_<3>><3>>.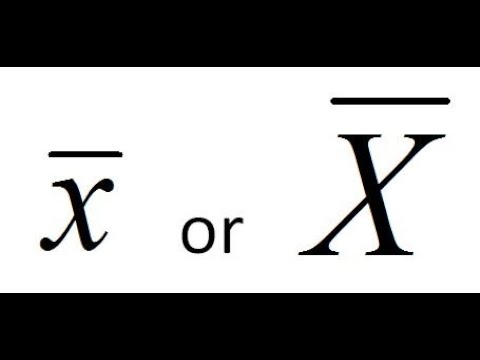 f(x)dx.>

Здесь подразумевается, что a.>»> b > a . <displaystyle b>a.> a.>»/>

Некоторые проблемы применения среднего [ править | править код ]

Отсутствие робастности [ править | править код ]

Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.

Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа.

Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.

Сложный процент [ править | править код ]

Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое.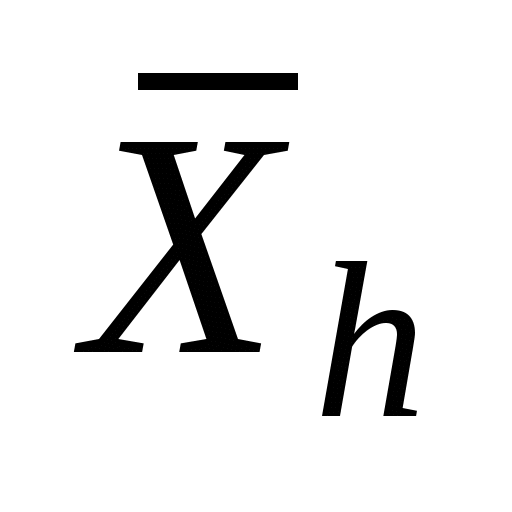 Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.

Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.

Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года всего на $5.1, средний рост в 8,2 % даёт конечный результат $35.1:

[$30 (1 — 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: [$30 (1 + 0. <circ >>.

Во-вторых, в данном случае, значение 0° (эквивалентное 360°) будет геометрически лучшим средним значением, так как числа отклоняются от 0° меньше, чем от какого-либо другого значения (у значения 0° наименьшая дисперсия). Сравните:

• число 1° отклоняется от 0° всего на 1°;
• число 1° отклоняется от вычисленного среднего, равного 180°, на 179°.

Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).

Здесь легко и интересно общаться.

Присоединяйся!

в ворде набирай код – маркер перед знаком.

знак у, код 035F,Alt+X : результат ͟y снизу
k, 035E,Alt+X ; результат ͞k – сверху.
В символах есть коды. и волнистых, и прочих…: )

если в ворде то вставить символ или надстрочным шрифтом (в свойствах шривта поставить галочку надстрочныу и в нужном месте поставить черточку)

В ворде есть переход в формулы жми:
ВСТАВКА – ФОРМУЛЫ – ДИАКРИТИЧЕСКИЕ ЗНАКИ и выбирай знак, в квадратике пиши переменную.
А так есть мастера формул. Международный – это MathType. В нём можно сделать всё, только язык надо зхнать : TeX

1>

Как сделать верхнее подчеркивание в Ворде?

Помимо использования разных видов форматирования текста таких как: изменение шрифта, применение полужирного или курсивного начертания, иногда необходимо сделать верхнее подчеркивание в Ворде. Расположить черту над буквой довольно просто, рассмотрим несколько способов решения данной задачи.

С помощью «Диакритических знаков»

Благодаря панели символов сделать черточку сверху можно следующим образом.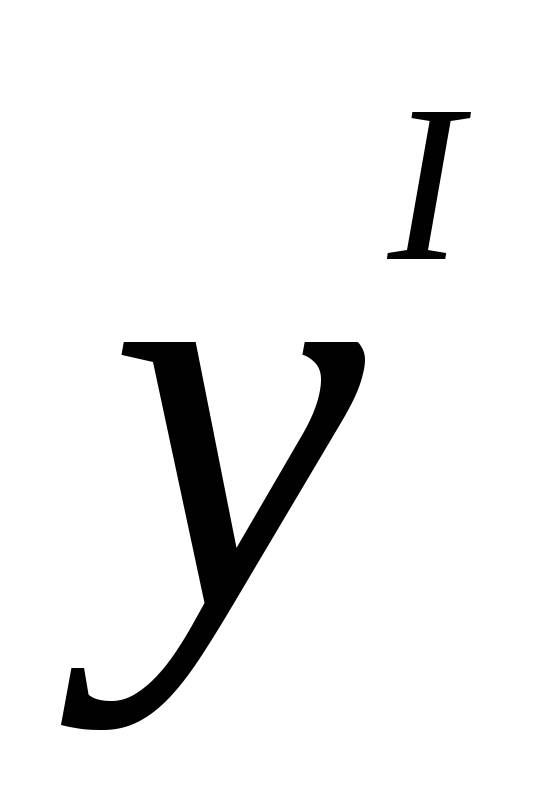 Установите курсор мыши в нужном месте по тексту. Перейдите во вкладку «Вставка» далее найдите и нажмите в области «Символы» на кнопку «Формула» и выберите из выпадающего меню «Вставить новую формулу».

Откроется дополнительная вкладка «Работа с формулами» или «Конструктор». Из представленных вариантов в области «Структуры» выберите «Диакритические знаки» и кликните по окну с названием «Черта».

В добавленном окне напечатайте необходимое слово или букву.

В результате получится такой вид.

Подчеркивание сверху посредством фигуры

Используя фигуры в Ворде, можно подчеркнуть слово как сверху, так и снизу. Рассмотрим верхнее подчеркивание. Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия».

Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.

 

Можно изменить цвет верхнего подчеркивания, нужно нажать по линии и открыть вкладку «Формат». Нажав по кнопке «Контур фигуры» указать нужный цвет. Также можно изменить вид подчеркивания и толщину. Для этого перейдите в подпункт ниже «Толщина» или «Штрихи».

В соответствии с настройками палочку можно преобразовать в штрихпунктирную линию, либо изменить на стрелку, в нужном направлении.

Благодаря таким простым вариантам, поставить черту над буквой или цифрой не займёт много времени. Стоит лишь выбрать наиболее подходящий способ из вышепредставленных.

Вставка математических знаков — Word

Основные математические символы	Нет	Часто используемые математические символы, такие как > и <
Греческие буквы	Строчные буквы	Строчные буквы греческого алфавита
	Прописные буквы	Прописные буквы греческого алфавита
Буквоподобные символы	Нет	Символы, которые напоминают буквы
Операторы	Обычные бинарные операторы	Символы, обозначающие действия над двумя числами, например + и ÷
	Обычные реляционные операторы	Символы, обозначающие отношение между двумя выражениями, такие как = и ~
	Основные N-арные операторы	Операторы, осуществляющие действия над несколькими переменными
	Сложные бинарные операторы	Дополнительные символы, обозначающие действия над двумя числами
	Сложные реляционные операторы	Дополнительные символы, обозначающие отношение между двумя выражениями
Стрелки	Нет	Символы, указывающие направление
Отношения с отрицанием	Нет	Символы, обозначающие отрицание отношения
Наборы знаков	Наборы знаков	Математический шрифт Script
	Готические	Математический шрифт Fraktur
	В два прохода	Математический шрифт с двойным зачеркиванием
Геометрия	Нет	Часто используемые геометрические символы

Таблица символов шрифта Горизонт

Таблица символов шрифта Горизонт

Таблица символов

•        ABCD
  #$%&
  1234

Латиница

AaBbCcDdEeFfGgHhIiJjKkLlMmNnOoPpQqRrSsTtUuVvWwXxYyZz

Кириллица

АаБбВвГгДдЕеЁёЖжЗзИиЙйКкЛлМмНнОоПпРрСсТтУуФфХхЦцЧчШшЩщЪъЫыЬьЭэЮюЯя

Цифры

0123456789

Пунктуация

. ∏∑√%‰

Надстрочные и подстрочные

⁰¹²³⁴⁵⁶⁷⁸⁹₀₁₂₃₄₅₆₇₈₉

Валюта

₿¢¤$€₴₽£¥

Числовые формы

½¼¾⅛⅜⅝⅞

Символы и стрелки

◊@&¶§©®™°|¦№↑↗→↘↓↙←↖

Дополнительная латиница-1

¡¢£¤¥¦§¨©«¬®¯°±²³´¶·¸¹»¼½¾¿ÀÁÂÃÄÅÆÇÈÉÊËÌÍÎÏÐÑÒÓÔÕÖ×ØÙÚÛÜÝÞßàáâãäåæçèéêëìíîïðñòóôõö÷øùúûüýþÿ

Латиница A

ĀāĂ㥹ĆćĊċČčĎďĐđĒēĖėĘęĚěĞğĠġĢģĦħĪīĮįİıĶķĹĺĻļĽľŁłŃńŅņŇňŌōŐőŒœŔŕŖŗŘřŚśŞşŠšŢţŤťŦŧŪūŮůŰűŲųŴŵŶŷŸŹźŻżŽž

Латиница B

ȘșȚț %name%

О символе

• Юникод: %unicode%
• Блок: %block%

Применение

• Copy-paste: %copyPaste%
• Windows: %windows%
• HTML: %html%

Основная латиница

!Восклицательный знак

0021

«Двойная кавычка (универсальная)

0022

%Знак процента

0025

‘Апостроф (одинарная кавычка)

0027

(Левая круглая скобка

0028

)Правая круглая скобка

0029

—Дефис-минус

002D

/Косая черта

002F

0Арабская цифра ноль

0030

1Арабская цифра один

0031

2Арабская цифра два

0032

3Арабская цифра три

0033

4Арабская цифра четыре

0034

5Арабская цифра пять

0035

6Арабская цифра шесть

0036

7Арабская цифра семь

0037

8Арабская цифра восемь

0038

9Арабская цифра девять

0039

;Точка с запятой

003B

<Знак меньше

003C

>Знак больше

003E

?Знак вопроса

003F

@Символ собака

0040

AЛатинская заглавная буква A

0041

BЛатинская заглавная буква B

0042

CЛатинская заглавная буква C

0043

DЛатинская заглавная буква D

0044

EЛатинская заглавная буква E

0045

FЛатинская заглавная буква F

0046

GЛатинская заглавная буква G

0047

HЛатинская заглавная буква H

0048

IЛатинская заглавная буква I

0049

JЛатинская заглавная буква J

004A

KЛатинская заглавная буква K

004B

LЛатинская заглавная буква L

004C

MЛатинская заглавная буква M

004D

NЛатинская заглавная буква N

004E

OЛатинская заглавная буква O

004F

PЛатинская заглавная буква P

0050

QЛатинская заглавная буква Q

0051

RЛатинская заглавная буква R

0052

SЛатинская заглавная буква S

0053

TЛатинская заглавная буква T

0054

UЛатинская заглавная буква U

0055

VЛатинская заглавная буква V

0056

WЛатинская заглавная буква W

0057

XЛатинская заглавная буква X

0058

YЛатинская заглавная буква Y

0059

ZЛатинская заглавная буква Z

005A

[Левая квадратная скобка

005B

\Обратная косая черта

005C

]Правая квадратная скобка

005D

^Знак вставки (циркумфлекс)

005E

_Нижнее подчёркивание

005F

aЛатинская строчная буква a

0061

bЛатинская строчная буква b

0062

cЛатинская строчная буква c

0063

dЛатинская строчная буква d

0064

eЛатинская строчная буква e

0065

fЛатинская строчная буква f

0066

gЛатинская строчная буква g

0067

hЛатинская строчная буква h

0068

iЛатинская строчная буква i

0069

jЛатинская строчная буква j

006A

kЛатинская строчная буква k

006B

lЛатинская строчная буква l

006C

mЛатинская строчная буква m

006D

nЛатинская строчная буква n

006E

oЛатинская строчная буква o

006F

pЛатинская строчная буква p

0070

qЛатинская строчная буква q

0071

rЛатинская строчная буква r

0072

sЛатинская строчная буква s

0073

tЛатинская строчная буква t

0074

uЛатинская строчная буква u

0075

vЛатинская строчная буква v

0076

wЛатинская строчная буква w

0077

xЛатинская строчная буква x

0078

yЛатинская строчная буква y

0079

zЛатинская строчная буква z

007A

{Левая фигурная скобка

007B

|Вертикальная линия

007C

}Правая фигурная скобка

007D

Дополнительная латиница-1

¡Перевернутый восклицательный знак

00A1

¢Знак цента и сентаво

00A2

£Знак фунта

00A3

¤Знак валюты

00A4

¦Изломанная вертикальная черта

00A6

©Знак авторского права

00A9

«Открывающая левая кавычка «ёлочка»

00AB

¬Знак отрицания

00AC

®Зарегистрированный товарный знак

00AE

¯Макрон.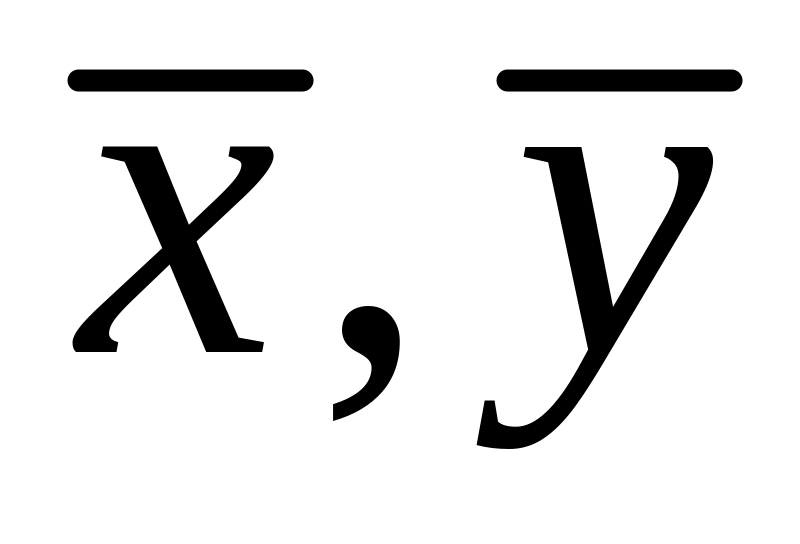 Надчёркивание

00AF

°Знак градуса

00B0

±Знак плюс-минус

00B1

²Верхний индекс 2

00B2

³Верхний индекс 3

00B3

´Знак ударения

00B4

¶Знак абзаца

00B6

·Точка по центру

00B7

¹Верхний индекс 1

00B9

»Закрывающая правая кавычка «ёлочка»

00BB

¼Дробь – одна четверть

00BC

½Дробь – одна вторая

00BD

¾Дробь – три четверти

00BE

¿Перевернутый вопросительный знак

00BF

ÀЛатинская заглавная буква A с грависом

00C0

ÁЛатинская заглавная буква A с акутом

00C1

ÂЛатинская заглавная буква A с циркумфлексом

00C2

ÃЛатинская заглавная буква A с тильдой

00C3

ÄЛатинская заглавная буква A с диэризисом

00C4

ÅЛатинская заглавная буква A с кружочком сверху

00C5

ÆЛатинская заглавная буква AE

00C6

ÇЛатинская заглавная буква C с седилью

00C7

ÈЛатинская заглавная буква E с грависом

00C8

ÉЛатинская заглавная буква E с акутом

00C9

ÊЛатинская заглавная буква E с циркумфлексом

00CA

ËЛатинская заглавная буква E с диэрезисом

00CB

ÌЛатинская заглавная буква I с грависом

00CC

ÍЛатинская заглавная буква I с акутом

00CD

ÎЛатинская заглавная буква I с циркумфлексом

00CE

ÏЛатинская заглавная буква I с диэрезисом

00CF

ÐЛатинская заглавная буква ETH

00D0

ÑЛатинская заглавная буква N с тильдой

00D1

ÒЛатинская заглавная буква O с грависом

00D2

ÓЛатинская заглавная буква O с акутом

00D3

ÔЛатинская заглавная буква O с циркумфлексом

00D4

ÕЛатинская заглавная буква O с тильдой

00D5

ÖЛатинская заглавная буква O с диэризисом

00D6

×Знак умножения

00D7

ØЛатинская заглавная буква O со штрихом

00D8

ÙЛатинская заглавная буква U с грависом

00D9

ÚЛатинская заглавная буква U с акутом

00DA

ÛЛатинская заглавная буква U с циркумфлексом

00DB

ÜЛатинская заглавная буква U с диэризисом

00DC

ÝЛатинская заглавная буква Y с акутом

00DD

ÞЛатинская заглавная буква торн

00DE

ßЛатинская строчная буква эсцет (S острое)

00DF

àЛатинская строчная буква a с грависом

00E0

áЛатинская строчная буква a с акутом

00E1

âЛатинская строчная буква a с циркумфлексом

00E2

ãЛатинская строчная буква a с тильдой

00E3

äЛатинская строчная буква a с диэризисом

00E4

åЛатинская строчная буква a с кружочком сверху

00E5

æЛатинская строчная лигатура ae

00E6

çЛатинская строчная буква c с седилью

00E7

èЛатинская строчная буква e с грависом

00E8

éЛатинская строчная буква e с акутом

00E9

êЛатинская строчная буква e с циркумфлексом

00EA

ëЛатинская строчная буква e с диэризисом

00EB

ìЛатинская строчная буква i с грависом

00EC

íЛатинская строчная буква i с акутом

00ED

îЛатинская строчная буква i с циркумфлексом сверху

00EE

ïЛатинская строчная буква i с диэризисом (умляутом)

00EF

ðЛатинская строчная буква eth

00F0

ñЛатинская строчная буква n с тильдой

00F1

òЛатинская строчная буква o с грависом

00F2

óЛатинская строчная буква o с ударением

00F3

ôЛатинская строчная буква o с циркумфлексом

00F4

õЛатинская строчная буква o с тильдой

00F5

öЛатинская строчная буква o с диэризисом

00F6

÷Знак деления

00F7

øЛатинская строчная буква o со штрихом

00F8

ùЛатинская строчная буква u с грависом

00F9

úЛатинская строчная буква u с акутом

00FA

ûЛатинская строчная буква u с циркумфлексом

00FB

üЛатинская строчная буква u с диэризисом

00FC

ýЛатинская строчная буква y с акутом

00FD

þЛатинская строчная буква торн

00FE

ÿЛатинская строчная буква y с диэризисом

00FF

Расширенная латиница-A

ĀЛатинская заглавная буква «A» с макроном

0100

āЛатинская строчная буква «a» с макроном

0101

ĂЛатинская заглавная буква «A» с бревисом

0102

ăЛатинская строчная буква «a» с бревисом

0103

ĄЛатинская заглавная буква «A» с огонэком

0104

ąЛатинская строчная буква «a» с огонэком

0105

ĆЛатинская заглавная буква «C» с акутом

0106

ćЛатинская строчная буква «c» с акутом

0107

ĊЛатинская заглавная буква «С» с точкой сверху

010A

ċЛатинская строчная буква «c» с точкой сверху

010B

ČЛатинская заглавная буква «C» с гачеком

010C

čЛатинская строчная буква «c» с гачеком

010D

ĎЛатинская заглавная буква «D» с гачеком

010E

ďЛатинская строчная буква «d» с гачеком

010F

ĐЛатинская заглавная буква «D» со штрихом

0110

đЛатинская строчная буква «d» со штрихом

0111

ĒЛатинская заглавная буква «E» с макроном

0112

ēЛатинская строчная буква «e» с макроном

0113

ĖЛатинская заглавная буква «E» с точкой сверху

0116

ėЛатинская строчная буква «e» с точкой сверху

0117

ĘЛатинская заглавная буква «E» с огонэком

0118

ęЛатинская строчная буква «e» с огонэком

0119

ĚЛатинская заглавная буква «E» с гачеком

011A

ěЛатинская строчная буква «e» с гачеком

011B

ĞЛатинская заглавная буква «G» с бревисом

011E

ğЛатинская строчная буква «g» с бревисом

011F

ĠЛатинская заглавная буква «G» с точкой сверху

0120

ġЛатинская строчная буква «g» с точкой сверху

0121

ĢЛатинская заглавная буква «G» с седилью

0122

ģЛатинская строчная буква «g» с седилью

0123

ĦЛатинская заглавная буква «H» со штрихом

0126

ħЛатинская строчная буква «h» со штрихом

0127

ĪЛатинская заглавная буква «I» с макроном

012A

īЛатинская строчная буква «i» с макроном

012B

ĮЛатинская заглавная буква «I» с огонэком

012E

įЛатинская строчная буква «i» с огонэком

012F

İЛатинская заглавная буква «I» с точкой сверху

0130

ıЛатинская строчная буква «i» без точки

0131

ĶЛатинская заглавная буква «K» с седилью

0136

ķЛатинская строчная буква «k» с седилью

0137

ĹЛатинская заглавная буква «L» с акутом

0139

ĺЛатинская строчная буква «l» с акутом

013A

ĻЛатинская заглавная буква «L» с седилью

013B

ļЛатинская строчная буква «l» с седилью

013C

ĽЛатинская заглавная буква «L» с гачеком

013D

ľЛатинская строчная буква «l» с гачеком

013E

ŁЛатинская заглавная буква «L» со штрихом, символ Лайткоина

0141

łЛатинская строчная буква «l» со штрихом

0142

ŃЛатинская заглавная буква «N» с акутом

0143

ńЛатинская строчная буква «n» с акутом

0144

ŅЛатинская заглавная буква «N» с седилью

0145

ņЛатинская строчная буква «n» с седилью

0146

ŇЛатинская заглавная буква «N» с гачеком

0147

ňЛатинская строчная буква «n» с гачеком

0148

ŌЛатинская заглавная буква «O» с макроном

014C

ōЛатинская строчная буква «o» с макроном

014D

ŐЛатинская заглавная буква «O» с двойным акутом

0150

őЛатинская строчная буква «o» с двойным акутом

0151

ŒЛатинская заглавная лигатура OE

0152

œЛатинская строчная лигатура oe

0153

ŔЛатинская заглавная буква «R» с акутом

0154

ŕЛатинская строчная буква «r» с акутом

0155

ŖЛатинская заглавная буква «R» с седилью

0156

ŗЛатинская строчная буква «r» с седилью

0157

ŘЛатинская заглавная буква «R» с гачеком

0158

řЛатинская строчная буква «r» с гачеком

0159

ŚЛатинская заглавная буква «S» с акутом

015A

śЛатинская строчная буква «s» с акутом

015B

ŞЛатинская заглавная буква «S» с седилью

015E

şЛатинская строчная буква «s» с седилью

015F

ŠЛатинская заглавная буква «S» с гачеком

0160

šЛатинская строчная буква «s» с гачеком

0161

ŢЛатинская заглавная буква «T» с седилью

0162

ţЛатинская строчная буква «t» с седилью

0163

ŤЛатинская заглавная буква «T» с гачеком

0164

ťЛатинская строчная буква «t» с гачеком

0165

ŦЛатинская заглавная буква «T» со штрихом

0166

ŧЛатинская строчная буква «t» со штрихом

0167

ŪЛатинская заглавная буква «U» с макроном

016A

ūЛатинская строчная буква «u» с макроном

016B

ŮЛатинская заглавная буква «U» с кружком сверху

016E

ůЛатинская строчная буква «u» с кружком сверху

016F

ŰЛатинская заглавная буква «U» с двойным акутом

0170

űЛатинская строчная буква «u» с двойным акутом

0171

ŲЛатинская заглавная буква «U» с огонэком

0172

ųЛатинская строчная буква «u» с огонэком

0173

ŴЛатинская заглавная буква «W» с циркумфлексом

0174

ŵЛатинская строчная буква «w» с циркумфлексом

0175

ŶЛатинская заглавная буква «Y» с циркумфлексом

0176

ŷЛатинская строчная буква «y» с циркумфлексом

0177

ŸЛатинская заглавная буква «Y» с диэрезисом

0178

ŹЛатинская заглавная буква «Z» с акутом

0179

źЛатинская строчная буква «z» с акутом

017A

ŻЛатинская заглавная буква «Z» с точкой сверху

017B

żЛатинская строчная буква «z» с точкой сверху

017C

ŽЛатинская заглавная буква «Z» с гачеком

017D

žЛатинская строчная буква «z» с гачеком

017E

Расширенная латиница-B

ȘЛатинская заглавная буква s с запятой снизу

0218

șЛатинская строчная буква s с запятой снизу

0219

ȚЛатинская заглавная буква t с запятой снизу

021A

țЛатинская строчная буква t с запятой снизу

021B

Некомбинируемые протяжённые символы-модификаторы

ʼМодификатор буквы апостроф

02BC

ˆМодификатор буквы циркумфлекс ударение

02C6

˙Точкой сверху

02D9

˚Кольцо сверху

02DA

˜Строчная тильде

02DC

˝Двойное акут ударение

02DD

Комбинируемые диакритические знаки

̀Комбинируемый гравис (тяжёлое ударение)

0300

́Комбинируемый акут (лёгкое ударение)

0301

̂Комбинируемый циркумфлекс (облечённое ударение)

0302

̃Комбинируемая тильда

0303

̄Комбинируемый макрон

0304

̆Комбинируемое бреве (бревис, кратка)

0306

̇Комбинируемая надстрочная точка

0307

̈Комбинируемое надстрочное двоеточие (умляут, диэрезис)

0308

̊Комбинируемый надстрочный кружок

030A

̋Комбинируемый двойной акут (венгерский умляут)

030B

̌Комбинируемая птичка над буквой

030C

̦Комбинируемая подстрочная запятая

0326

̧Комбинируемая седиль

0327

̨Комбинируемый огонэк (c-образный хвостик)

0328

Кириллица

ЁКириллическая заглавная буква ё

0401

ЂКириллическая заглавная буква дьже

0402

ЃКириллическая заглавная буква гэ

0403

ЄКириллическая заглавная буква якорное Е

0404

ЅКириллическая заглавная буква дзе

0405

ІКириллическая заглавная буква и десятеричное

0406

ЇКириллическая заглавная буква йи

0407

ЈКириллическая заглавная буква йе

0408

ЉКириллическая заглавная буква ле

0409

ЊКириллическая заглавная буква нье

040A

ЋКириллическая заглавная буква гервь

040B

ЌКириллическая заглавная буква кэ

040C

ЎКириллическая заглавная буква у краткое

040E

ЏКириллическая заглавная буква дже

040F

АКириллическая заглавная буква а

0410

БКириллическая заглавная буква бэ

0411

ВКириллическая заглавная буква вэ

0412

ГКириллическая заглавная буква гэ

0413

ДКириллическая заглавная буква дэ

0414

ЕКириллическая заглавная буква е

0415

ЖКириллическая заглавная буква же

0416

ЗКириллическая заглавная буква зэ

0417

ИКириллическая заглавная буква и

0418

ЙКириллическая заглавная буква и краткое

0419

ККириллическая заглавная буква ка

041A

ЛКириллическая заглавная буква эл

041B

МКириллическая заглавная буква эм

041C

НКириллическая заглавная буква эн

041D

ОКириллическая заглавная буква о

041E

ПКириллическая заглавная буква пэ

041F

РКириллическая заглавная буква эр

0420

СКириллическая заглавная буква эс

0421

ТКириллическая заглавная буква тэ

0422

УКириллическая заглавная буква У

0423

ФКириллическая заглавная буква эФ

0424

ХКириллическая заглавная буква ха

0425

ЦКириллическая заглавная буква цэ

0426

ЧКириллическая заглавная буква че

0427

ШКириллическая заглавная буква ша

0428

ЩКириллическая заглавная буква ща

0429

ЪКириллическая заглавная буква твёрдый знак

042A

ЫКириллическая заглавная буква ы

042B

ЬКириллическая заглавная буква мягкий знак

042C

ЭКириллическая заглавная буква э

042D

ЮКириллическая заглавная буква ю

042E

ЯКириллическая заглавная буква я

042F

аКириллическая строчная буква а

0430

бКириллическая строчная буква бэ

0431

вКириллическая строчная буква вэ

0432

гКириллическая строчная буква гэ

0433

дКириллическая строчная буква дэ

0434

еКириллическая строчная буква е

0435

жКириллическая строчная буква же

0436

зКириллическая строчная буква зэ

0437

иКириллическая строчная буква и

0438

йКириллическая строчная буква и краткое

0439

кКириллическая строчная буква ка

043A

лКириллическая строчная буква эл

043B

мКириллическая строчная буква эм

043C

нКириллическая строчная буква эн

043D

оКириллическая строчная буква о

043E

пКириллическая строчная буква пэ

043F

рКириллическая строчная буква эр

0440

сКириллическая строчная буква эс

0441

тКириллическая строчная буква тэ

0442

уКириллическая строчная буква у

0443

фКириллическая строчная буква эф

0444

хКириллическая строчная буква ха

0445

цКириллическая строчная буква цэ

0446

чКириллическая строчная буква че

0447

шКириллическая строчная буква ша

0448

щКириллическая строчная буква ща

0449

ъКириллическая строчная буква твёрдый знак

044A

ыКириллическая строчная буква ы

044B

ьКириллическая строчная буква мягкий знак

044C

эКириллическая строчная буква э

044D

юКириллическая строчная буква ю

044E

яКириллическая строчная буква я

044F

ёКириллическая строчная буква ё

0451

ђКириллическая строчная буква дьже

0452

ѓКириллическая строчная буква гэ

0453

єКириллическая строчная буква якорное е

0454

ѕКириллическая строчная буква дзе

0455

іКириллическая строчная буква и десятеричное

0456

їКириллическая строчная буква йи

0457

јКириллическая строчная буква йе

0458

љКириллическая строчная буква ле

0459

њКириллическая строчная буква нье

045A

ћКириллическая строчная буква гервь

045B

ќКириллическая строчная буква ке

045C

ўКириллическая строчная буква у краткое

045E

џКириллическая строчная буква дже

045F

ѢКириллическая заглавная буква ять

0462

ҐКириллическая заглавная буква г с подъемом

0490

ґКириллическая строчная буква г с подъемом

0491

ҚКириллическая заглавная буква к с подстрочным элементом литеры

049A

ҺКириллическая заглавная буква ша

04BA

ӨКириллическая заглавная буква полосатая o

04E8

Дополнительная расширенная латиница

ẀЛатинская заглавная буква w с грависом

1E80

ẁЛатинская строчная буква w с грависом

1E81

ẂЛатинская заглавная буква w с акутом

1E82

ẃЛатинская строчная буква w с акутом

1E83

ẄЛатинская заглавная буква w с диэрезисом

1E84

ẅЛатинская строчная буква w с диэрезисом

1E85

ỲЛатинская заглавная буква y с грависом

1EF2

ỳЛатинская строчная буква y с грависом

1EF3

Знаки пунктуации

​Пробел нулевой ширины

200B

‑Неразрывный дефис

2011

‒Цифровое тире

2012

–Среднее тире

2013

—Длинное тире

2014

‘Открывающая одинарная кавычка

2018

’Закрывающая одинарная кавычка

2019

‚Нижняя одинарная открывающая кавычка

201A

“Закрывающая двойная кавычка

201C

”Правая двойная кавычка

201D

„Нижняя двойная открывающая кавычка

201E

•Точка маркер списка

2022

…Многоточие

2026

‰Знак промилле

2030

‹Одинарная открывающая (левая) французская угловая кавычка

2039

›Одинарная закрывающая (правая) французская угловая кавычка

203A

⁄Дробная наклонная черта

2044

Надстрочные и подстрочные знаки

⁰Надстрочный нуль

2070

⁴Верхний индекс четыре

2074

⁵Верхний индекс пять

2075

⁶Верхний индекс шесть

2076

⁷Верхний индекс семь

2077

⁸Верхний индекс восемь

2078

⁹Верхний индекс девять

2079

₀Подстрочный индекс ноль

2080

₁Подстрочный индекс один

2081

₂Подстрочный индекс два

2082

₃Подстрочный индекс три

2083

₄Подстрочный индекс четыре

2084

₅Подстрочный индекс пять

2085

₆Подстрочный индекс шесть

2086

₇Подстрочный индекс семь

2087

₈Подстрочный индекс восемь

2088

₉Подстрочный индекс девять

2089

Символы валют

₴Знак гривны

20B4

₽Знак рубля

20BD

Буквоподобные символы

№Знак номера

2116

™Знак торговой марки

2122

Числовые формы

⅛Простая дробь одна восьмая

215B

⅜Простая дробь три восьмые

215C

⅝Простая дробь пять восьмых

215D

⅞Простая дробь семь восьмых

215E

Стрелки

←Стрелка влево

2190

↑Стрелка вверх

2191

→Стрелка направо

2192

↓Стрелка вниз

2193

↖Стрелка влево-вверх

2196

↗Стрелка вправо-вверх

2197

↘Стрелка вправо-вниз

2198

↙Стрелка влево-вниз

2199

Математические операторы

∏N-арное произведение

220F

∑N-ичное суммирование

2211

−Знак минус

2212

√Квадратный корень

221A

≈Почти равный

2248

≤Меньше или равный

2264

≥Больше чем или равно

2265

Геометрические фигуры

◼Черный квадрат в середине

25FC

Поддерживаемые языки

• Русский
• Английский
• Албанский
• Баскский
• Белорусский
• Болгарский
• Венгерский
• Датский
• Ирландский
• Исландский
• Испанский
• Итальянский
• Карельский
• Латышский
• Литовский
• Македонский
• Немецкий
• Норвежский
• Польский
• Португальский
• Румынский
• Сербский
• Словацкий
• Словенский
• Турецкий
• Туркменский
• Украинский
• Финский
• Французский
• Чешский
• Шведский
• Эстонский

Русский

Эти ящерицы чешут вперёд за ключом, но багаж в сейфах, поди подъедь. ..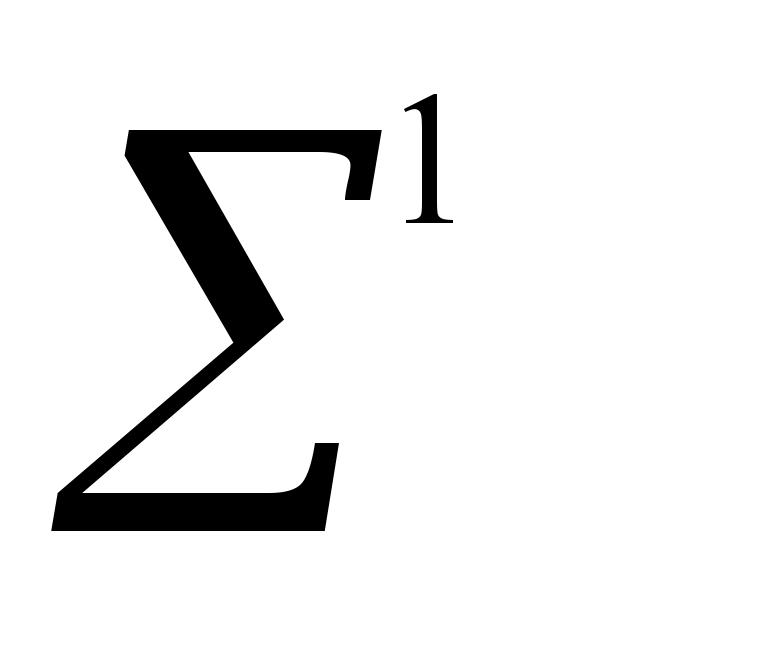

Португальский

À noite, vovô Kowalsky vê o ímã cair no pé do pingüim queixoso e vovó põe açúcar no chá de tâmaras do jabuti feliz

Французский

Bâchez la queue du wagon-taxi avec les pyjamas du fakir

Английский

Two hardy boxing kangaroos jet from Sydney to Zanzibar on quicksilver pinions.

Немецкий

«Fix, Schwyz!» quäkt Jürgen blöd vom Paß

Румынский

Gheorghe, obezul, a reuşit să obţină jucându-se un flux în Quebec de o mie kilowaţioră

Белорусский

Я жорстка заб’ю проста ў сэрца гэты расквечаны профіль, што ходзіць ля маёй хаты.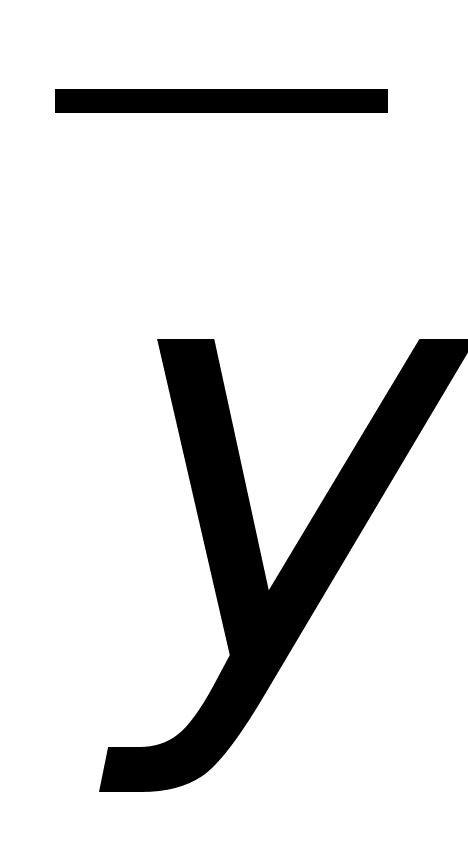

Болгарский

Жълтата дюля беше щастлива, че пухът, който цъфна, замръзна като гьон

Датский

Quizdeltagerne spiste jordbær med fløde, mens cirkusklovnen Walther spillede på xylofon

Исландский

Kæmi ný öxi hér ykist þjófum nú bæði víl og ádrepa

Испанский

El veloz murciélago hindú comía feliz cardillo y kiwi

Итальянский

Pranzo d’acqua fa volti sghembi

Латышский

Ķieģeļu cepējs Edgars Buls fraku un hūti žāvē uz čīkstošām eņģēm

Литовский

Įlinkdama fechtuotojo špaga sublykčiojusi pragręžė apvalų arbūzą

Норвежский

Høvdingens kjære squaw får litt pizza i Mexico by

Польский

O, mógłże sęp chlań wyjść furtką bździn

Сербский

Дебљој згужвах смеђ филц — њен шкрт џепчић

Словацкий

Kŕdeľ šťastných ďatľov učí pri ústí Váhu mĺkveho koňa obhrýzať kôru a žrať čerstvé mäso

Словенский

Piškur molče grabi fižol z dna cezijeve hoste

Турецкий

Pijamalı hasta, yağız şoföre çabucak güvendi

Украинский

В Бахчисараї фельд’єґер зумів одягнути ящірці жовтий капюшон!

Финский

Viekas kettu punaturkki laiskan koiran takaa kurkki

Чешский

Příliš žluťoučký kůň úpěl ďábelské ódy

Шведский

Yxskaftbud, ge vår wczonmö iqhjälp

Эстонский

Põdur Zagrebi tšellomängija-följetonist Ciqo külmetas kehvas garaažis

Заказать дизайн. ..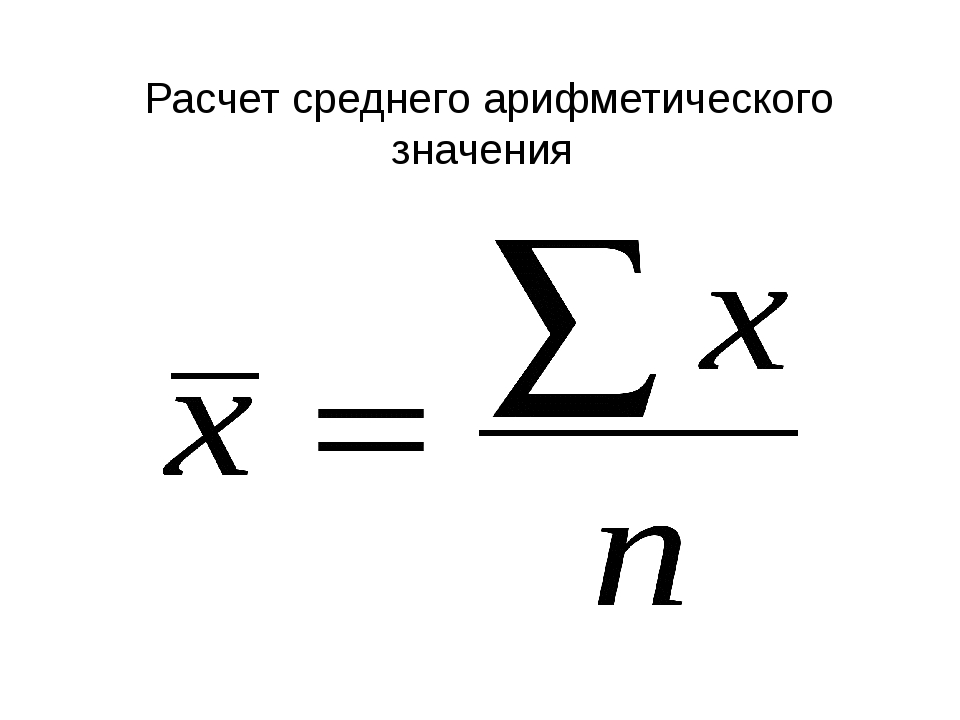

Перечень специальных символов — Документация Qucs Help 0.0.19

В компоненте “Текст” и в тексте меток осей диаграмм можно использовать специальные символы. Это делается с помощью тэгов LaTeX. В следующей таблице приводится перечень символов, имеющихся в настоящее время.

Примечание: Правильное отображение этих символов зависит от шрифта, используемого Qucs!

Строчные греческие буквы

Тэг LaTeX	Юникод	Описание
\alpha	0x03B1	alpha
\beta	0x03B2	beta
\gamma	0x03B3	gamma
\delta	0x03B4	delta
\epsilon	0x03B5	epsilon
\zeta	0x03B6	zeta
\eta	0x03B7	eta
\theta	0x03B8	theta
\iota	0x03B9	iota
\kappa	0x03BA	kappa
\lambda	0x03BB	lambda
\mu	0x03BC	mu
\textmu	0x00B5	mu
\nu	0x03BD	nu
\xi	0x03BE	xi
\pi	0x03C0	pi
\varpi	0x03D6	pi
\rho	0x03C1	rho
\varrho	0x03F1	rho
\sigma	0x03C3	sigma
\tau	0x03C4	tau
\upsilon	0x03C5	upsilon
\phi	0x03C6	phi
\chi	0x03C7	chi
\psi	0x03C8	psi
\omega	0x03C9	omega

Прописные греческие буквы

Тэг LaTeX	Юникод	Описание
\Gamma	0x0393	Gamma
\Delta	0x0394	Delta
\Theta	0x0398	Theta
\Lambda	0x039B	Lambda
\Xi	0x039E	Xi
\Pi	0x03A0	Pi
\Sigma	0x03A3	Sigma
\Upsilon	0x03A5	Upsilon
\Phi	0x03A6	Phi
\Psi	0x03A8	Psi
\Omega	0x03A9	Omega

Математические символы

Тэг LaTeX	Юникод	Описание
\cdot	0x00B7	знак умножения — точка (центрированная точка)
\times	0x00D7	знак умножения — крестик
\pm	0x00B1	знак плюс минус
\mp	0x2213	знак минус плюс
\partial	0x2202	знак частного дифференцирования
\nabla	0x2207	набла-оператор
\infty	0x221E	знак бесконечности
\int	0x222B	знак интеграла
\approx	0x2248	символ приближения (волнистый знак равенства)
\neq	0x2260	знак не равно
\in	0x220A	символ “содержится в”
\leq	0x2264	знак меньше-равно
\geq	0x2265	знак больше-равно
\sim	0x223C	(центрально-европейский) знак пропорциональности
\propto	0x221D	(американский) знак пропорциональности
\diameter	0x00F8	знак диаметра (также знак среднего)
\onehalf	0x00BD	половина
\onequarter	0x00BC	четверть
\twosuperior	0x00B2	квадрат (степень 2)
\threesuperior	0x00B3	степень 3
\ohm	0x03A9	единица для сопротивления (прописная греческая омега)

back to the top

Таблица символов

Пользователей: 4051 Новичок: nix1111 Предыдущая ветка системы

Таблица Символов ASCII символы HTML код Dec код Hex код Вид символа Описание Греческие буквы HTML код Dec код Hex код Вид символа Описание Стрелки HTML код Dec код Hex код Вид символа Описание Прочие символы HTML код Dec код Hex код Вид символа Описание Знаки пунктуации HTML код Dec код Hex код Вид символа Описание Общая пунктуация HTML код Dec код Hex код Вид символа Описание Знаки регистрации и авторских прав HTML код Dec код Hex код Вид символа Описание Знаки валют HTML код Dec код Hex код Вид символа Описание

Как сделать длинное и среднее тире на клавиатуре или в Word

Любой документ, будь то официальный или персональный, должен быть оформлен красиво, чтобы с ним было приятно работать. Один из важных моментов в оформлении документа — это простановка знаков тире и дефисов. Визуально это очень схожие знаки препинания, но все же отличия есть. В нашей статье о том, какие можно поставить тире и дефисы на клавиатуре, в Word и других программах.

---

Оглавление: 
1. Виды тире и дефисов
2. Как сделать среднее тире
- На клавиатуре
- В Word
3. Как сделать длинное тире
- На клавиатуре
- В Word

---

Виды тире и дефисов

Важно

На клавиатуре есть только одна кнопка, которая способна вывести горизонтальную палочку. Эта палочка является дефисом, не тире.

Дефис — это знак, который используется для разделения части слов на слоги или частей составных слов. Чтобы было понятнее, приведем несколько примеров. “Кол-во”, “р-н”, “45-й”, “по-русски” и так далее. Во всех этих словах используется дефис, который можно поставить просто с клавиатуры.

Тире — это знак, который разделяет слова в предложении. Слева и справа от тире обязательно должны быть пробелы. Принято разделять 2 вида тире: среднее и длинное. По-английски тире — это dash. Принято разделять “EN dash” и “EM dash”, соответственно, среднее и длинное тире.

Обратите внимание

Принято считать, что “настоящее” тире для текстов — это длинное тире, то есть “EM dash”. Тогда как среднее тире применяется, например, для указания диапазона чисел “1941–1945”. Но упрощения, связанные с печатным набором текста, привели к тому, что в англоязычной литературе среднее тире заменило длинное тире.

После небольшой теории покажем наглядно, как отличаются дефис, среднее тире и длинное тире:

Дефис	N-N
Среднее тире	N–N
Длинное тире	N—N

Визуально отличия заметны невооруженным взглядом. Более того, знаки тире располагаются выше, чем знак дефис.

Обратите внимание

Из таблицы выше вы можете скопировать нужное тире (или дефис) и вставить их в свой текст.

Как сделать среднее тире

Рассмотрим несколько способов поставить среднее тире.

На клавиатуре

Способ 1:

Проще всего сделать среднее тире на клавиатуре, которая имеет дополнительный NUM-блок — это блок цифр с правой части клавиатуры. Если этот блок имеется, активируйте его (нажатие клавиши Num Lock). Далее зажмите Ctrl и нажмите на дефис в блоке NUM. После этого будет установлено среднее тире.

Важно

Во многих программах комбинация клавиш “Ctrl + минус” выполняет некие заданные действия. Например, в браузере уменьшает страницу. При использовании этой комбинации в таких программах, работать простановка среднего тире не будет.

Способ 2:

Как и в первом способе, потребуется клавиатура с NUM-блоком. Активируйте его нажатием на клавишу Num Lock. После этого зажмите клавишу Alt и введите комбинацию цифр “0150”. Появится среднее тире.

Плюс этого способа, в сравнении с первым вариантом, является его универсальность — он работает практически везде.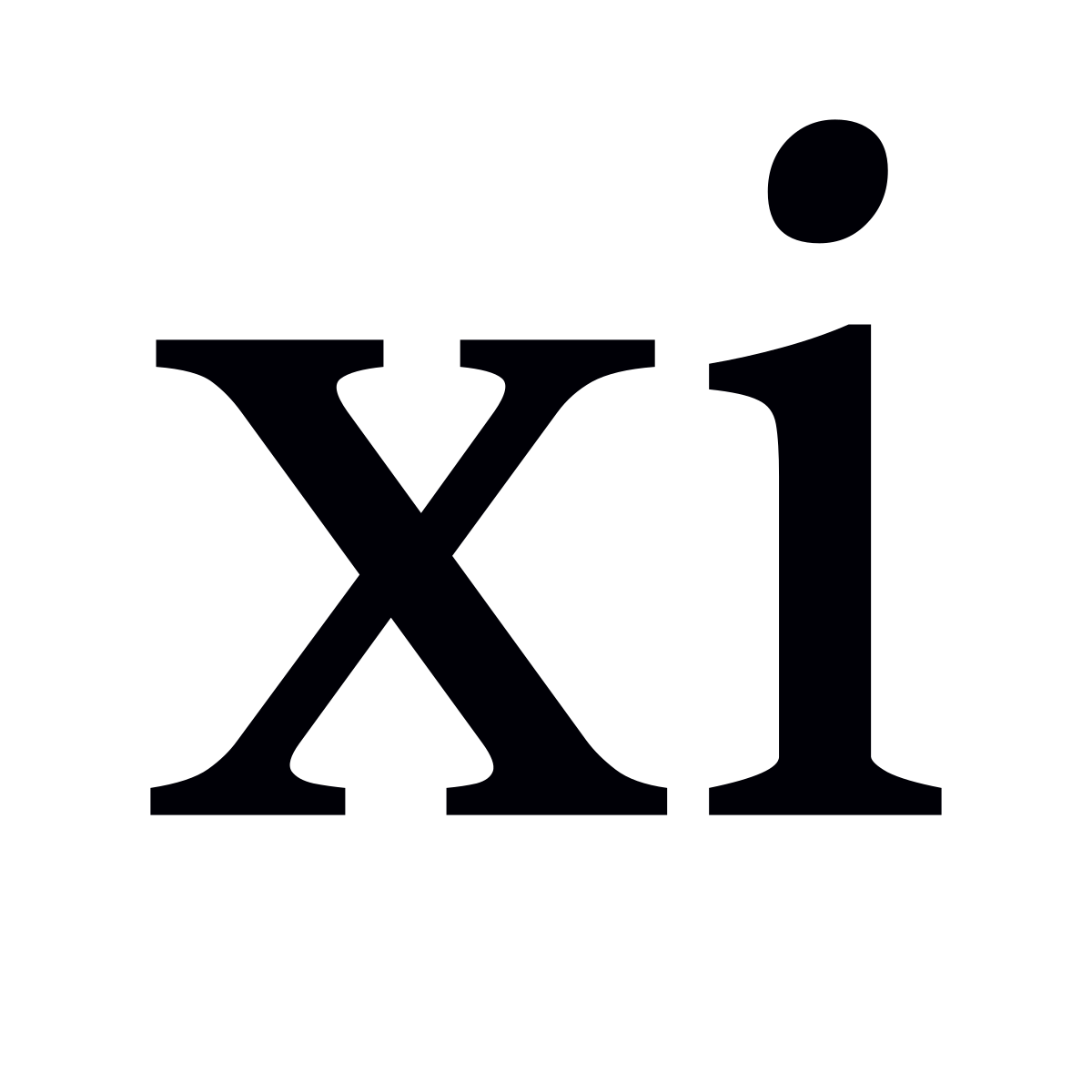

Способ 3:

Снова будет задействован NUM-блок и определенная комбинация клавиш. Нужно ввести при помощи NUM-блока комбинацию “2013”, а после нажать одновременно сочетание клавиш “Alt+X”. Цифры 2013 превратятся в среднее тире.

Этот способ работает не везде. Но, например, он работает в Word.

В Word

Отдельно рассмотрим способы поставить среднее тире в Word.

Способ 1:

Самый простой способ поставить среднее тире в Word — это воспользоваться автоматической заменой. По-умолчанию приложение Word устанавливает среднее тире, если вы поставили знак дефиса (минус), оставили слева и справа от него по пробелу, а также поставили пробел после первого слова, которое следует за знаком.

Например, при написании фразы “Свобода — это рабство” в Word дефис заменится на тире автоматически после нажатия на клавишу пробел после слова “это”.

Способ 2:

Второй вариант — вставить среднее тире из библиотеки символов Word.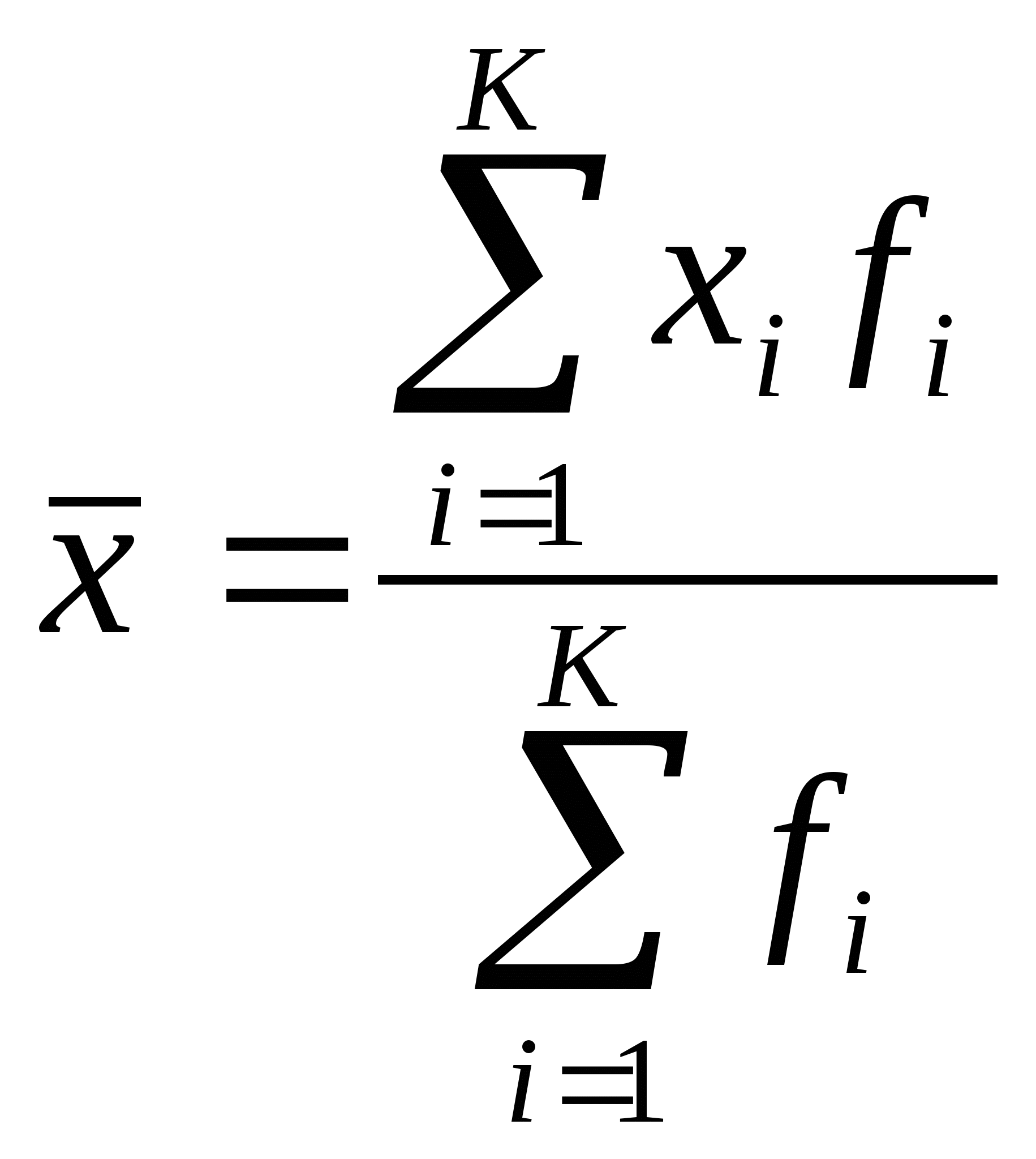 Чтобы это сделать, перейдите в верхнем меню программы в раздел “Вставка”. Выберите пункт “Символ”, а далее нажмите “Другие символы”.

Откроется библиотека символов Word. Перейдите в раздел “Знаки пунктуации”, и здесь вы увидите список доступных символов. В том числе, среди них будет среднее тире. Нажмите на него, и после этого нажмите “Вставить”.

Обратите внимание

Около символа будет указано, что это “EN Dash”.

Как сделать длинное тире

Теперь посмотрим на наиболее удобные способы поставить длинное тире в текст.

На клавиатуре

Способ 1:

Для установки длинного тире достаточно зажать клавиши “Ctrl+Alt” и нажать на правом цифровом блоке (NUM-блок) на значок “-”. После этого будет установлено длинное тире.

Способ 2:

Как и в случае со средним тире, длинное можно поставить при помощи специальной комбинации цифр. Напишите при помощи правого NUM-блока код “2014”, а после этого нажмите сочетание клавиш “Alt+X” и произойдет автоматическая замена числа на длинное тире.

Способ 3:

Если на клавиатуре есть две клавиши Alt (одна слева от пробела, другая справа от пробела), можно использовать правую клавишу Alt для простановки длинного тире. Зажмите ее и нажмите на значок “-” на NUM-блоке. После этого будет проставлено длинное тире.

Способ 4:

Зажмите на клавиатуре левую клавишу “Alt” и после этого введите комбинацию при помощи NUM-блока “0151” — будет вставлено длинное тире.

В Word

Теперь отдельно рассмотрим способы вставить длинное тире в Word.

Обратите внимание

Все перечисленные выше варианты работают, в том числе, в Word.

Способ 1:

Используйте вставку символов. Для этого в верхнем меню переключитесь на пункт “Вставка”, выберите вариант “Символ” и пункт “Другие символы”.

Появится таблица символов, переключитесь к набору “Знаки пунктуации” и установите длинное тире, выбрав его из списка знаков.

Обратите внимание

У длинного тире указано, что это “EM Dash”.

Способ 2:

В Word можно настроить автоматическую замену определенного символьного сочетания на нужный символ (или группу символов). Это можно использовать для простановки длинного тире, если с ним приходится часто работать.

Нажмите в верхнем меню Word на раздел “Вставка”, после этого кликните “Символ” и выберите “Другие символы”.

Переключившись к набору “Знаки пунктуации”, найдите длинное тире в списке доступных символов. Выберите его и нажмите на пункт “Автозамена”.

Здесь в левой колонке “Заменить” напишите комбинацию, которую вы хотели бы, чтобы Word автоматически менял на длинное тире. Например, два дефиса. После этого нажмите “Добавить” и “ОК”.

Все, с этого момента два дефиса будут заменяться на одно длинное тире.

Загрузка…

Юникод

Unicode — это стандарт программирования для кодирования письменных символов и текста в операционных системах по всему миру (https://en. wikipedia.org/wiki/Unicode). Поскольку математика обычно используется в компьютерах, использующих стандарт Unicode, как для вычисления результатов, так и для набора текста, этот веб-сайт ссылается на стандарт Unicode в предоставляемых им ресурсах символов. См. Перечисленные ниже страницы для навигации по математическим символам Юникода на этом сайте.

Каждый символ в стандарте Unicode описывается кодовой точкой , которая представляет собой шестнадцатеричное значение, однозначно идентифицирующее символ.На этом веб-сайте указана точка Unicode для каждого математического символа, где префикс U + используется, чтобы указать, что шестнадцатеричное значение является кодовой точкой Unicode. Например, символ (пи) имеет кодовую точку, показанную ниже.

Кодовые точки

кодируются на основе формата кодирования операционной системы: UTF-8 , UTF-16 или UTF-32 . Вот почему стандарт описывается как формат переменной ширины . Например, символ кодируется с использованием двух однобайтовых (8-битных) кодовых единиц в формате UTF-8 и одной двухбайтовой (16-битной) кодовых единиц в формате UTF-16 .Кодировки символа ( U + 03C0 ) показаны ниже.

Формат	Кодировка
UTF-8	0xCF 0x80
UTF-16	0x03C0

На этом веб-сайте используется формат UTF-8 . Все символы в стандарте Unicode могут быть описаны с использованием от одного до четырех однобайтовых (8-битных) кодовых единиц с использованием формата UTF-8 . Примечание , ресурсы символов не предоставляют кодировки Unicode для математических символов, а только кодовые точки.

Math иногда использует комбинацию символов стандарта Unicode для объединения двух глифов в новый символ. Например, символ (x bar) представляет собой комбинацию латинской строчной буквы x ( U + 0078 ) и объединяющего символа макрона ( U + 0304 ). Это показано на диаграмме ниже.

Обратите внимание: объединяющий символ следует за символом, с которым он объединяется.Современная альтернатива сочетанию символов — использование математической системы набора, где команды с ударением позволяют добиться того же эффекта. Например, символ x bar будет описан как обычный текст \ bar {x} вместо комбинированного символа.

Ниже приведены комбинированные символы, упомянутые на этом сайте.

Языки программирования со временем стали более дружелюбными при работе со стандартом Unicode. В этом примере показано, как кодировать и декодировать некоторые математические символы Юникода.Для кодирования комбинированного символа с помощью javascript можно использовать следующий синтаксис.

  console.log ("\ u {0078} \ u {0304}") // выводит x̄ (x bar)
  

Это эквивалентно следующему выражению.

  console.log ("x \ u {0304}") // выводит x̄ (x bar)
  

Обратите внимание: по виду этого результата можно подумать, что длина этой строки составляет 1 , но на самом деле это 2 , как показано ниже.

  console.log ("x̄".length) // выводит 2
  

Наконец, вот функция, которая печатает кодовые точки, составляющие строку.

  функция анализа (ов) {
  console.log ("ввод:" + s)
  console.log ("длина:" + s.length)
  for (let i = 0; i  

Дан следующий ввод:

Функция производит вывод:

  ввод: x̄
длина: 2
U + 0078
U + 0304
  

TeX - популярная система набора для создания технических документов и, в частности, математических выражений.

Набор математических символов, сгруппированных по тому, как они используются в математике.

Эта таблица содержит символы Юникода, которые используются в математике. Каждый символ имеет кодовую точку Unicode, имя, теги и ключевое слово.

Греческая строчная буква π (пи) - геометрическая константа, приблизительно равная 3,1416. Числовое значение равно длине окружности любого круга, деленной на его диаметр.

Столбец x используется в статистике для представления выборочного среднего значения распределения.

Работа с x-полосой (x̄) и p-hat (p̂) в статистике

Исправлено 23 октября 2012 г.

Мне часто задают вопрос (по крайней мере, распространенный в терминах Unicode): каков код для символа p-hat (p̂) и символов x-bar (x̄) в статистике. Хотя это общие символы, они не превратились в единый символ в Unicode (так же, как термодинамические точечные символы наполовину отсутствуют, если они также не присутствуют в системе правописания староирландского или другого иностранного языка.

Хорошая новость в том, что они могут быть созданы в Unicode, но это необычно. Уловка здесь в том, чтобы забыть математику и думать о фонетике. Существует механизм для размещения любого диакритического знака / диакритического знака над любой буквой с использованием одного из сочетаний диакритических знаков . Это диакритические знаки с диакритическими знаками. Это диакритические знаки с диакритическими знаками.

На нашем дочернем сайте, Penn State Computing with Accents Diacritics, есть список различных диакритических знаков для HTML, но я объясню, как это работает для x̄ и p x

HTML

Для HTML я рекомендую ввести базовую букву ( x или p ), а затем соответствующий числовой escape-код для комбинированного диакритического знака.p , а не p̂ , проблема обычно в шрифте. Относительно небольшое количество шрифтов поддерживает хорошее сочетание диакритических знаков (даже математические шрифты не поддерживают диакритические знаки). Те, которые это делают, ориентированы на фонетику , и включают в себя:

Первые два шрифта поставляются Microsoft / Apple, обычно устанавливаются и также включают математические символы ... но это шрифты без засечек. Если вам нужен шрифт с засечками, вы можете указать один из других фонетических шрифтов с засечками, а затем указать пользователям на него (но укажите Arial Unicode / Lucida Grande в качестве резервных копий).На данный момент это не очень красивое решение.

Word и т. Д.

А теперь самое интересное начинается. Вы можете ввести эти символы в других программах (см. Ниже), но их редактирование будет странным (см. Ниже). Вот процедура:

1. Переключитесь на шрифт, который поддерживает комбинирование диакритических знаков, и введите базовую букву (в данном случае x или p ).
2. Введите пробел и переместите курсор назад (вы благодарите меня за этот совет):
3. Затем вы можете вставить объединяющий диакритический знак:
   1. С картой символов (Windows) или палитрой символов (Mac) ИЛИ:
   2. С помощью кода Alt в Word для Windows или кода параметра на шестнадцатеричной клавиатуре Mac. См. Коды на http://tlt.its.psu.edu/suggestions/international/bylanguage/ipavowels.html Код ALT Word / Windows для x̄ x ALT + 0772 . Шестнадцатеричный код Option для Mac x Option + 0304

Когда вы редактируете, вы обнаружите, что иногда вы удаляете ударение, а иногда вы удаляете букву под ударением (очень интересно). Вам может потребоваться отменить удаление , переместите курсор с помощью клавиш со стрелками , когда это произойдет.Не всегда похоже, что курсор движется, но это текст в Юникоде. Когда вы пытаетесь набрать назализованный open-o / ɔ̃ /, вы действительно получаете некоторую практику ....

Общие статистические формулы - статистические решения

Статистические формулы используются для расчета значений, связанных со статистическими концепциями или анализами. Здесь мы обсудим общие формулы и их значение.

Среднее по численности населения

Термин "среднее значение совокупности", который представляет собой средний балл совокупности по заданной переменной, представлен следующим образом:

μ = (Σ X i ) / N

Символ «μ» представляет среднее значение генеральной совокупности.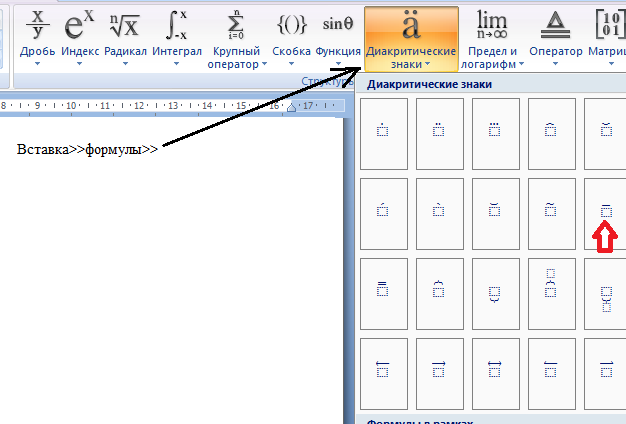 Символ «Σ X i » представляет собой сумму всех баллов, имеющихся в популяции (скажем, в данном случае) X 1 X 2 X 3 и так далее. Символ «N» обозначает общее количество людей или заболевших в популяции.

Получите одобрение вашей диссертации
Мы работаем с аспирантами каждый день и знаем, что нужно для одобрения вашего исследования.

• Отзыв адресной комиссии
• Дорожная карта до завершения
• Определите свои потребности и сроки

Стандартное отклонение населения

Стандартное отклонение совокупности - это мера разброса (изменчивости) оценок по заданной переменной и представлена ​​как:

σ = sqrt [Σ (X i - μ) 2 / N]

Символ «σ» представляет стандартное отклонение генеральной совокупности.Термин «sqrt», используемый в этой статистической формуле, означает квадратный корень. Термин «Σ (X i - μ) 2 », используемый в статистической формуле, представляет собой сумму квадратов отклонений оценок от их среднего значения по совокупности.

Разница в численности населения

Дисперсия генеральной совокупности - это квадрат стандартного отклонения генеральной совокупности и представлена ​​следующим образом:

σ 2 = Σ (X i - μ) 2 / N

Символ «σ 2» представляет дисперсию генеральной совокупности.

Среднее значение

Среднее значение выборки - это средний балл выборки по заданной переменной, который представлен следующим образом:

x_bar = (Σ x i ) / n

Термин «x_bar» представляет собой выборочное среднее. Символ «Σ x i », используемый в этой формуле, представляет собой сумму всех оценок, присутствующих в выборке (скажем, в данном случае) x 1 x 2 x 3 и так далее. Символ «n» обозначает общее количество людей или наблюдений в выборке.

Стандартное отклонение выборки

Статистика, называемая стандартным отклонением выборки, является мерой разброса (изменчивости) оценок в выборке по заданной переменной и представлена ​​следующим образом:

s = sqrt [Σ (x i - x_bar) 2 / (n - 1)]

Термин «Σ (x i - x_bar) 2 » представляет собой сумму квадратов отклонений оценок от среднего по выборке.

Вариант выборки

Дисперсия выборки представляет собой квадрат стандартного отклонения выборки и представлена ​​следующим образом:

с 2 = Σ (x i - x_bar) 2 / (n - 1)

Символ «s 2 » представляет дисперсию выборки.

Стандартное отклонение объединенной выборки

Стандартное отклонение объединенной выборки - это взвешенная оценка разброса (изменчивости) по нескольким выборкам. Представлен:

s p = sqrt [(n 1 - 1) * s 1 2 + (n 2 - 1) * s 2 2 ] / (n 1 + n 2 - 2)]

Термин «s p » представляет стандартное отклонение объединенной выборки. Термин «n 1 » представляет размер первой выборки, а термин «n 2 » представляет размер второй выборки, которая объединяется с первой выборкой.Термин «s 1 2 » представляет дисперсию первой выборки, а «s 2 2 » представляет дисперсию второй выборки.

Intellectus позволяет проводить и интерпретировать результаты анализа за считанные минуты. Щелкните ссылку ниже, чтобы создать бесплатную учетную запись, и начните анализировать свои данные прямо сейчас!

Попробовать

Statistics Solutions может помочь с количественным анализом, помогая разработать методологию и главы с результатами. Услуги, которые мы предлагаем, включают:

План анализа данных

Измените свои исследовательские вопросы и нулевые / альтернативные гипотезы

Напишите план анализа данных; указать конкретную статистику для ответа на вопросы исследования, допущения статистики и обосновать, почему они являются подходящей статистикой; предоставить ссылки

Обоснуйте размер вашей выборки / анализ мощности, предоставьте ссылки

Объясните вам свой план анализа данных, чтобы вы чувствовали себя комфортно и уверенно.

Два часа дополнительной поддержки у вашего статистика

Раздел количественных результатов (Описательная статистика, двумерный и многомерный анализ, моделирование структурных уравнений, анализ траектории, HLM, кластерный анализ)

Чистый и кодовый набор данных

Проведение описательной статистики (т.е., среднее значение, стандартное отклонение, частота и процент, в зависимости от случая)

Проведите анализ для изучения каждого из вопросов вашего исследования

Результаты повторной записи

Предоставьте APA 6 -е издание , таблицы и рисунки

Объясните выводы главы 4

Постоянная поддержка всей статистики по главам результатов

Пожалуйста, позвоните по номеру 727-442-4290, чтобы запросить расценки на основе специфики вашего исследования, расписания с использованием календаря на его странице или по электронной почте [адрес электронной почты защищен]

Что означает выборка? Символ (X Bar), определение и стандартная ошибка - Zippia

Немногое имеет большее значение для роста и успеха бизнеса, чем их усилия по статистическому анализу.Он предоставляет информацию, необходимую для разработки стратегического планирования и принятия решений. В основе статистики лежит использование выборок, позволяющих делать прогнозы, применимые к большим группам населения.

Обращение к выборочному среднему - это ступенька для формирования более широких выводов и развития.

Что такое среднее значение выборки?

Среднее значение выборки определяется как среднее значение данного набора выборок. Среднее значение выборки математически представлено как x. Это считается отправной точкой для начала дальнейшего анализа.

Обычно находят выборочное среднее, чтобы преобразовать это значение в более сложную и подробную формулу, такую ​​как центральная тенденция и стандартное отклонение выборочного набора.
Концепция выборочного среднего возникнет на раннем этапе изучения статистики.

Почему важно среднее значение выборки?

Самым очевидным преимуществом расчета выборочного среднего является то, что он может предоставить информацию, которая точно применима к большей совокупности. Это важно, поскольку позволяет получить статистическую информацию без выполнения невыполнимой задачи опроса всех вовлеченных лиц.

Кроме того, среднее значение выборки используется в различных отраслях промышленности. Любая область, связанная с научными исследованиями, например биология и химия, будет использовать выборочное среднее на ранних этапах своих конкретных исследований. Ввод данных и ИТ-задания используют выборочные средние значения для достижения повседневных целей. Даже в бизнесе выборочное среднее необходимо для завершения расчетов темпов роста.

Хотя вы можете смутно вспомнить примерное среднее как отдаленное воспоминание из школьной математики, оно применяется во многих областях и может быть экспоненциально полезным по многим причинам.

Как рассчитать выборочное среднее

Математика любого рода изначально может вызывать стресс у многих людей, но вычисление выборочного среднего - одно из самых простых вычислений, которые вы найдете в статистике.

Как и любое другое стандартное статистическое уравнение, вам необходимо выполнить определенную формулу и шаги, чтобы получить правильное среднее значение выборки. Прежде чем пытаться найти среднее значение для вашей организации, вы должны сначала рассмотреть формулу.

Формула для решения выборочного среднего: x̄ = (Σxi) / n

На первый взгляд на эту формулу, возможно, вы уже готовы отказаться от нее, но сложный, казалось бы, язык уравнения на самом деле довольно легко разложить.

• В уравнении x & # 772 представляет искомый ответ, который является выборочным средним.

• Символ Σ - это математический способ сказать: «сложите следующие числа».

• Продолжение xi в круглых скобках означает «все значения x», которые будут значениями для каждого фрагмента данных, который вы исследуете.

• Наконец, уравнение просит вас разделить на n, которое обозначает общее количество сравниваемых значений.

Это очень много, но давайте рассмотрим это шаг за шагом. Чтобы лучше понять процесс нахождения выборочного среднего, рассмотрим шаги с точки зрения следующего примера.

Компания-оператор телефонной связи заинтересована в получении более подробной информации о статистических тенденциях своей клиентской базы. Чтобы начать этот процесс, они должны определить выборочное среднее. Они решают сравнить итоговую клиентскую базу за последние шесть месяцев, чтобы получить среднее количество людей, пользующихся их услугами.

Телефонная компания записывает следующие значения для каждого из шести месяцев:

• Январь - 20000 клиентов

• Февраль -18000 клиентов

• март - 20 400 клиентов

• апрель - 21050 клиентов

• Май - 23000 клиентов

• июнь - 22 300 клиентов

1. Сложите значения. На первом этапе нахождения выборочного среднего мы просим сложить все значения в выборке.Чтобы применить это к примеру с телефонной компанией, они начинают с суммирования количества клиентов, которых они имели каждый месяц.

   20 000 + 18 000 + 20 400 + 21 050 + 23 000 + 22 300 = 124 750

   Число 124 750 представляет собой общее количество клиентов, которые телефонный провайдер имел за шестимесячный размер выборки.

2. Определите значение n. Значение n в уравнении для выборочного среднего представляет, сколько элементов сравнивается.Поскольку телефонная компания сравнивает ежемесячное количество клиентов за шесть месяцев, значение n в этом примере будет 6.

3. Введите значения и разделите. Последний шаг к вычислению выборочного среднего - ввести значения, которые вы определили, в исходное уравнение и разделить для решения. Для телефонной компании это будет означать, что они разделят 124 750 на 6, чтобы получить среднее значение по выборке.

   124,750 / 6 = 20,792

   Выборочное среднее значение клиентской базы телефонной компании за шесть месяцев составляет 20 792 человека.

Что такое отклонение?

Дисперсия означает, насколько разбросаны числа в наборе. Хотя вы получили среднее значение с помощью формулы выборочного среднего, вычисление дисперсии набора покажет вам, насколько далеко друг от друга находится каждое значение в наборе.

Хотя дисперсия является важной величиной, которую нужно знать само по себе, основная цель построения этого уравнения состоит в том, чтобы иметь возможность завершить процесс определения стандартной ошибки набора позже.

Как рассчитать дисперсию

После того, как вы найдете выборочное среднее для вашего набора, вы можете использовать его, чтобы найти дисперсию.

Выполните следующие шаги, чтобы определить дисперсию набора образцов.

1. Вычтите выборочное среднее из каждого значения. Чтобы начать поиск дисперсии, вам нужно будет вычесть выборочное среднее, которое вы только что обнаружили, из каждого значения в наборе. В случае с телефонной компанией это будет означать вычитание 20 792 из стоимости каждого месяца.

   (20,000-20,792) (18,000-20,792) (20,400-20,792) (21,050-20,792) (23,000-29,792) (22,300-20,792) = (-792, -2,792, -392, 258, 2,028, 1,328)

2. Возведите полученные значения в квадрат. После вычитания выборочного среднего из каждого значения продолжите, возводя в квадрат каждое из новых чисел, которые у вас остались. В примере с телефонной компанией возведение в квадрат каждого значения приведет к получению новых значений:

   .

   (627,264) (7,795,264) (153,664) (66,564) (4,112,784) (1,763,584)

3. Заполните формулу выборочного среднего. Последним шагом к определению дисперсии в наборе является добавление новых значений, которые вы нашли путем вычитания и возведения в квадрат исходной формулы выборочного среднего.Завершите уравнение, как обычно, чтобы получить дисперсию выборки.

   (627,264) + (7,795,264) + (153,664) + (66,564) + (4,112,784) + (1,763,584) = 14,519,124

   14 519 124/6 = 2 419 854

Размер ответа описывает, насколько велика дисперсия в наборе. Результат из примера с телефонным оператором имеет чрезвычайно высокую степень дисперсии, что означает большую разницу между каждым из значений.

Если мы вернемся к исходным данным о том, сколько клиентов у компании было в месяц, мы увидим, что это расхождение очевидно.В период с января по февраль у провайдера произошло резкое падение на 2 000 клиентов всего за один месяц, за которым последовали более существенные всплески. Разница в этих исходных значениях - это то, что влияет на результат формулы дисперсии.

Что такое стандартная ошибка?

Стандартная ошибка также является мерой того, как числа распределены по набору, но оценивает, насколько каждая точка данных отличается от среднего значения по сравнению друг с другом. Это также известно как скорость распределения.

Хотя выборочное среднее дает информацию о среднем по выборке, а дисперсия измеряет разницу между каждым значением в выборке, стандартная ошибка немного отличается.

В большинстве распределений все значения будут находиться в пределах двух стандартных отклонений от среднего, если только оно не является выбросом.

Как рассчитать стандартную ошибку

Для расчета выборочного среднего и дисперсии требуется как минимум несколько шагов для завершения процесса. Однако вы уже выполнили большую часть работы по поиску стандартной ошибки после выполнения этих уравнений.Нахождение стандартной ошибки установленной пост-дисперсии - это всего лишь один шаг.

1. Найдите квадратный корень из значения дисперсии. Для определения стандартной ошибки по значению дисперсии требуется только найти квадратный корень из этого числа. В примере с телефонной компанией мы найдем квадратный корень из 2 419 854, чтобы определить стандартную ошибку.

   √2,419,854 = 1,556

   Стандартная ошибка для выборки телефонной компании - 1,556.Это очень большое стандартное отклонение, означающее, что значения, удаленные от среднего значения выборки, разбросаны и более неточны для применения к более крупной выборке. Другими словами, данные, полученные в телефонной компании, демонстрируют противоречивые выборочные значения и не будут репрезентативными для средних значений телефонной отрасли в целом.

Дополнительный пример

Профессор колледжа хочет знать статистику успеваемости по последнему тесту, который он дал своему классу.

Результаты теста для класса были: (82, 88, 83, 89, 91, 79, 85, 93, 83)

Он начинает процесс оценивания, складывая все значения тестов в своем классе и деля результат на 9 - количество учеников в классе.

82 + 88 + 83 + 89 + 91 + 79 + 85 + 93 + 83 = 773

773/9 = 85,89

Выборочное среднее значение тестовых баллов в классе профессора составляет 85,89. Он продолжает, решая разницу между оценками теста.Это делается путем вычитания среднего выборочного значения 85,89 из каждого значения и возведения полученных чисел в квадрат.

(82-85,89) (88-85,89) (83-85,89) (89-85,89) (91-85,89) (79-85,89) (85-85,89) (93-85,89) (83-85,89) = (-3,89 , 2,11, -2,89, 3,11, 5,11, -6,89, -0,89, 7,11, -2,89)

(-3,89, 2,11, -2,89, 3,11, 5,11, -6,89, -0,89, 7,11, -2,89) ² = (15,13, ​​4,45, 8,35, 9,67, 26,11, 47,47, 0,79, 50,55, 8,35)

Чтобы завершить решение для дисперсии, профессор вставляет новые значения, которые он нашел, и решает, используя формулу выборочного среднего.

(15,13 + 4,45 + 8,35 + 9,67 + 26,11 + 47,47 + 0,79 + 50,55 + 8,35) = 170,87

170,87 / 9 = 18,99

Разница между оценками в этом тесте составляет 18,99, что свидетельствует о значительных различиях между оценками, но ничего необычного.

Теперь, когда профессор накопил все необходимые ему значения, он возводит в квадрат результат дисперсии, чтобы найти стандартную ошибку набора выборки класса.

√18,99 = 4,36

Стандартная ошибка оценок за тест 4.36. Это означает, что большинство оценок в классе находятся в пределах 4,36 балла выше или ниже среднего значения 85,89.

Никогда не упускайте возможность, которая подходит именно вам.
Начать

Общие математические символы и терминология

Математические символы и терминология могут сбивать с толку и мешать изучению и пониманию основ математики.

Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.

Мы что-то упускаем? Дайте нам знать.

---

Общие математические символы

+ сложение, плюс, положительное

Символ сложения + обычно используется для обозначения того, что два или более чисел следует сложить вместе, например, 2 + 2.

Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2. На нашей странице Положительные и отрицательные числа объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.

Подробнее см. На нашей странице Дополнение .

---

- вычитание, минус, отрицание

Этот символ имеет два основных применения в математике:

1. - используется, когда нужно вычесть одно или несколько чисел, например, 2 - 2.
2. Символ - также обычно используется для обозначения отрицательного или отрицательного числа, например −2.

См. Дополнительную информацию на нашей странице Вычитание .

---

× или * или. Умножение

Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.

Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.

Реже умножение также может быть обозначено точкой.или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) совпадает с 2 × (3 + 2).

См. Дополнительную информацию на нашей странице Умножение .

---

÷ или / Подразделение

Оба эти символа используются для обозначения деления в математике. ÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.

/ используется в электронных таблицах и других компьютерных приложениях.

Подробнее см. На нашей странице Division .

---

= равно

Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычислений, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.

Вы также можете встретить другие похожие символы, хотя они встречаются реже:

• ≠ означает не равно.Например, 2 + 2 ≠ 5 - 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
• ≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
• ≈ означает приблизительно равно или почти равно. Две стороны отношения, обозначенные этим символом, будут , а не , которые будут достаточно точными для математических манипуляций.

---

<Меньше и> Больше

Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.

Этот символ > означает больше, например, 4> 2.

≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и> =.

≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.

± плюс или минус

Этот символ ± означает «плюс» или «минус». Он используется, например, для обозначения доверительных интервалов вокруг числа.

Ответом считается «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.

Например, 5 ± 2 на практике может быть любым числом от 3 до 7.

---

∑ Сумма

Символ ∑ означает сумму.

∑ - заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel - кнопка Автосумма имеет сигму в качестве значка.

---

° Градус

Градусы ° используются по-разному.

• В качестве меры вращения - угол между сторонами фигуры или вращение окружности. Круг равен 360 °, а прямой угол - 90 °. См. Наш раздел о Geometry для получения дополнительной информации.
• Мера температуры. градусов Цельсия или Цельсия используются в большинстве стран мира (за исключением США).Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется градус Фаренгейта. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.

---

∠ Угол

Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.

Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC можно использовать для описания угла точки A (между точками B и C).Подробнее об углах и других геометрических терминах см. На наших страницах Geometry .

---

√ Квадратный корень

√ - символ квадратного корня. Квадратный корень - это число, которое при умножении на себя дает исходное число.

Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.

См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.

---

ⁿ Мощность

Целое число с верхним индексом (любое целое число n ) - это символ, используемый для обозначения степени числа.

Например, 3 ² означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).

4 ³ означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.

См. Наши страницы Расчетная площадь и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .

Степень также используется как сокращенный способ записи больших и малых чисел.

Большие числа

10 ⁶ - 1 000 000 (один миллион).

10 ⁹ - 1 000 000 000 (один миллиард).

10 ¹² - 1 000 000 000 000 (один триллион).

10 ¹⁰⁰ , написанное длинной рукой, будет равно 1 с 100 нулями (один гугол).

Маленькие числа

10 ^-3 - 0,001 (одна тысячная)

10 ^-6 равно 0.6 = 10 ⁶ = 1000000 (один миллион).

---

. Десятичная точка

. - символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.

---

, Разделитель тысяч

Запятую можно использовать для разделения больших чисел и облегчения их чтения.

Тысячу можно записать как 1000, так и 1000, а миллион - как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.

В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.

В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и, действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .

---

[], () Скобки, круглые скобки

Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.

Части расчета, заключенные в квадратные скобки, вычисляются первыми, например

• 5 + 3 × 2 = 11
• (5 + 3) × 2 = 16

---

% В процентах

Символ% означает процент или число из 100.

Узнайте все о процентах на нашей странице: Введение в проценты

---

π Pi

π или пи - греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи - это длина окружности круга, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.

---

∞ Бесконечность

Символ ∞ означает бесконечность - понятие, согласно которому числа существуют вечно.

Каким бы большим у вас ни было число, вы всегда можете выбрать номер побольше, потому что вы всегда можете добавить к нему единицу.

Бесконечность - это не число, а идея чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, полюбить или ненавидеть.

---

\ (\ bar x \) (x-bar) Среднее значение

\ (\ bar x \) - среднее всех возможных значений x.

Чаще всего этот символ встречается в статистике.

См. Нашу страницу Среднее значение для получения дополнительной информации.

---

! Факториал

! это символ факториала.

н! - произведение (умножение) всех чисел от n до 1 включительно, т.е. n × (n − 1) × (n − 2) ×… × 2 × 1.

Например:

5! = 5 × 4 × 3 × 2 × 1 = 120

10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800

---

| Труба

Труба '|' также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.

Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) - это абсолютное значение или модуль \ (x \) .

Математически это определяется как

$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$

Проще говоря, \ (\ vert x \ vert \) - неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.

Он также используется в вероятности, где P (Z | Y) обозначает вероятность X при условии Y.

---

∝ Пропорциональный

∝ означает «пропорционально » и используется, чтобы показать что-то, что меняется по отношению к чему-то другому.

Например, если x = 2y, то x ∝ y.

---

∴ Следовательно

∴ - удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.

---

∵ Потому что

∵ - удобная сокращенная форма слова «потому что», не путать с «поэтому».

---

---

Математическая терминология (A-Z)

Амплитуда

Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда - это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.

Апофема

Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.

Площадь

Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах (м ² ).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .

Асимптота

Асимптота - это прямая линия или ось, которая конкретно связана с изогнутой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Встречается в геометрии и тригонометрии .

Ось

Опорная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.

Коэффициент

Коэффициент - это число или величина, умножающая другую величину. Обычно его ставят перед переменной . В выражении 6 x 6 - коэффициент, а x - переменная.

Окружность

Окружность - это длина расстояния по краю круга. Это тип с периметром , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу о изогнутых форм .

Данные

Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум - это отдельное значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.

Диаметр

Диаметр - это термин, используемый в геометрии для обозначения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза больше радиуса .

Экстраполировать

Экстраполяция - это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого нет данных, с выводом значений неизвестных данных из тенденций в известных данных.

Фактор

Коэффициент - это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное количество факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя - само себя и 1. Простой множитель - множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 - простые числа).

Среднее значение, медиана и мода

Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, среднее значение является средним значением. Режим - это число, которое встречается чаще всего.

Операция

Математическая операция - это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции - это сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .

Математические операции часто называют «суммами». Строго говоря, «сумма» - это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.

Периметр

Периметр двумерной фигуры - это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница Perimeter объясняет это более подробно.

Доля

Пропорция - это относительное отношение. Соотношения сравнивают одну часть с другой, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к дробям .

Пифагор

Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .

Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».

Количественный и качественный

Количественные данные - это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.

Качественные данные - это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.

Подробнее см. Нашу страницу о типах данных .

Радиан

Радиан - это единица СИ для измерения углов. Один радиан эквивалентен углу, образуемому в центре круга дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.

Радиус

Термин радиус используется в контексте кругов и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до его внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Для получения дополнительной информации см. Нашу страницу о изогнутых форм .

Диапазон

В статистике диапазон данного набора данных - это разница между наибольшим и наименьшим значениями.

Коэффициент

Соотношение - это математический термин, используемый для сравнения размеров одной детали с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.

Стандартное отклонение

Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону

Срок

Термин - это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).

Переменная

Переменная - это коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, которое может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x 6 - это коэффициент , а x - переменная.

Разница

Дисперсия - это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе находится от среднего и, следовательно, от каждого другого члена в наборе.

Вектор

Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например изучение движения, где скорость, ускорение, сила, смещение и импульс являются векторными величинами.

Объем

Объем - это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м ³ .

---

Дополнительная литература по навыкам, которые вам нужны

---

Руководство по навыкам, которые вам нужны

Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.

Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.

---

Обозначение

- Что означает фигурный символ x «$ \ mathcal {X} $» в «$ \; x_i \ in \ mathcal {X} \; $»? Обозначение

- Что означает фигурный символ x «$ \ mathcal {X} $» в «$ \; x_i \ in \ mathcal {X} \; $»? - Обмен стеками математики

Сеть обмена стеками

Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Mathematics Stack Exchange - это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 1 год назад

Просмотрено 265 раз

$ \ begingroup $

---

Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме форума Mathematics Stack Exchange.

Закрыт в прошлом году.

Если вам нужен более подробный контекст, это уравнение находится на второй странице этого документа. Я предполагаю, что это просто означает «любое значение, которое может иметь $ x $» или «все значения $ x $», но я просто хотел проверить.

Синий

5,3k1111 золотых знаков9797 серебряных знаков204204 бронзовых знака

Создан 28 июн.

тонкий

13944 бронзовых знака

$ \ endgroup $ 6 $ \ begingroup $

Заглавные буквы, такие как $ \ mathcal {X} $ (каллиграфия «X») на изображении, могут использоваться для обозначения набора; в данном случае это так.Однако это не всегда так, поскольку $ f \ substeq \ mathbb {R} \ times \ mathbb {R} $ (строчная буква «f») иногда используется для обозначения функции на $ \ mathbb {R} $. Вы также можете увидеть заглавные буквы, используемые для обозначения элемента набора, например, в определении предела последовательности. Это просто зависит от контекста и автора литературы.

Создан 30 июн.

Тейлор РендонТейлор Рендон

1,93622 золотых знака88 серебряных знаков2525 бронзовых знаков

$ \ endgroup $ 3

Не тот ответ, который вы ищете? Просмотрите другие вопросы с метками обозначения или задайте свой вопрос.

Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Некоторые математические символы

---

Умножение

Есть три широко используемых способа индикации умножения

• Обозначение « х », эл.g., 5 x 6 = 30. Обратите внимание, что этого символа обычно избегают в алгебраических уравнениях из-за общего использования «x» для обозначения неизвестной величины.
• Символ « * », например 5 * 8 = 40. Использование звездочки для обозначения умножения обычно используется в электронных таблицах (например, Excel) и в алгебраических выражениях.
• Или просто число рядом с выражением в скобках, например, 5 (6 + 2) = 40

Дивизион

Есть три обычно используемых способа обозначения деления.

• "/", например, 40/5 = 8
• "÷", например, 30 ÷ 5 = 6
• Деление также можно указать, поместив одну величину (числитель) над другой величиной (знаменатель), как показано ниже.

44/123 = 0,3577

Равно (=) и не равно (≠)

2 + 3 = 5

2 + 3 ≠ 4

(Читается как «не равно» или «не равно».

Меньше (

<) и больше (>)

• Символ <означает, что меньше .Например,

7 <8

200 <300

• Символ> означает больше . Например,

6> 4

3000> 2750

• Символ ≤ означает, что меньше или равно .
• Символ ≥ означает больше или равно .

Примерно равно

• Символ ≈ означает примерно равный .

---

Когда вам дается математическое выражение или уравнение, порядок, в котором выполняются математические операции, очень важен. Правила для этого довольно простые. Рассмотрим следующий пример:

2 + (7 + 3) * 3 ² + 4 * (3-1) + 10

Сначала это может показаться устрашающим, но на самом деле это довольно просто. Правила: кратко изложены в таблице ниже.

Порядок действий Решить в пределах круглых и квадратных скобок изнутри наружу Вычислить экспонентов Выполните Умножение и деление в порядке их появления. Выполните Сложение и Вычитание в порядке их появления.

Итак, в приведенном выше примере вы бы:

1. Решить в скобках
2. Вычислить экспоненты
3. Выполнить умножение и деление
4. Выполнить сложение и вычитание

И правильный ответ - 110.

вернуться наверх | предыдущая страница | следующая страница

.

No related posts.