∈ — Принадлежит: U+2208 isin
Значение символа
Принадлежит. Математические операторы.
Символ «Принадлежит» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия |  1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| bmg | 220B |
| Композиционное исключение | Нет |
| Изменение регистра | 2208 |
| Простое изменение регистра | 2208 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 88 88 | 226 136 136 | 14846088 | 11100010 10001000 10001000 |
| UTF-16BE | 22 08 | 34 8 | 00100010 00001000 | |
| UTF-16LE | 08 22 | 8 34 | 2082 | 00001000 00100010 |
| UTF-32BE | 00 00 22 08 | 0 0 34 8 | 8712 | |
| UTF-32LE | 08 22 00 00 | 8 34 0 0 | 136445952 | 00001000 00100010 00000000 00000000 |
± — Знак плюс-минус: U+00B1 plusmn
+-, сложить вычесть
U+00B1
Значение символа
Знак плюс-минус (±) используется для указания интервала.
Символ «Знак плюс-минус» был утвержден как часть Юникода версии 1.1 в 1993 г.
Этот текст также доступен на следующих языках: English; Deutsch;
Свойства
| Версия | 1. 1 |
| Блок | |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 00B1 |
| Простое изменение регистра | 00B1 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | C2 B1 | 49841 | 11000010 10110001 | |
| UTF-16BE | 00 B1 | 0 177 | 177 | 00000000 10110001 |
| UTF-16LE | B1 00 | 177 0 | 45312 | |
| UTF-32BE | 00 00 00 B1 | 0 0 0 177 | 177 | 00000000 00000000 00000000 10110001 |
| UTF-32LE | B1 00 00 00 | 177 0 0 0 | 2969567232 | 10110001 00000000 00000000 00000000 |
∙ — Оператор буллит: U+2219
скалярное умножение, знак умножения, умножить
U+2219
Значение символа
Оператор буллит.
Математические операторы.
Символ «Оператор буллит» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2219 |
| Простое изменение регистра | 2219 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 88 99 | 226 136 153 | 14846105 | 11100010 10001000 10011001 |
| UTF-16BE | 22 19 | 34 25 | 8729 | 00100010 00011001 |
| UTF-16LE | 19 22 | 25 34 | 6434 | 00011001 00100010 |
| UTF-32BE | 00 00 22 19 | 0 0 34 25 | 8729 | 00000000 00000000 00100010 00011001 |
| UTF-32LE | 19 22 00 00 | 25 34 0 0 | 421658624 | 00011001 00100010 00000000 00000000 |
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно».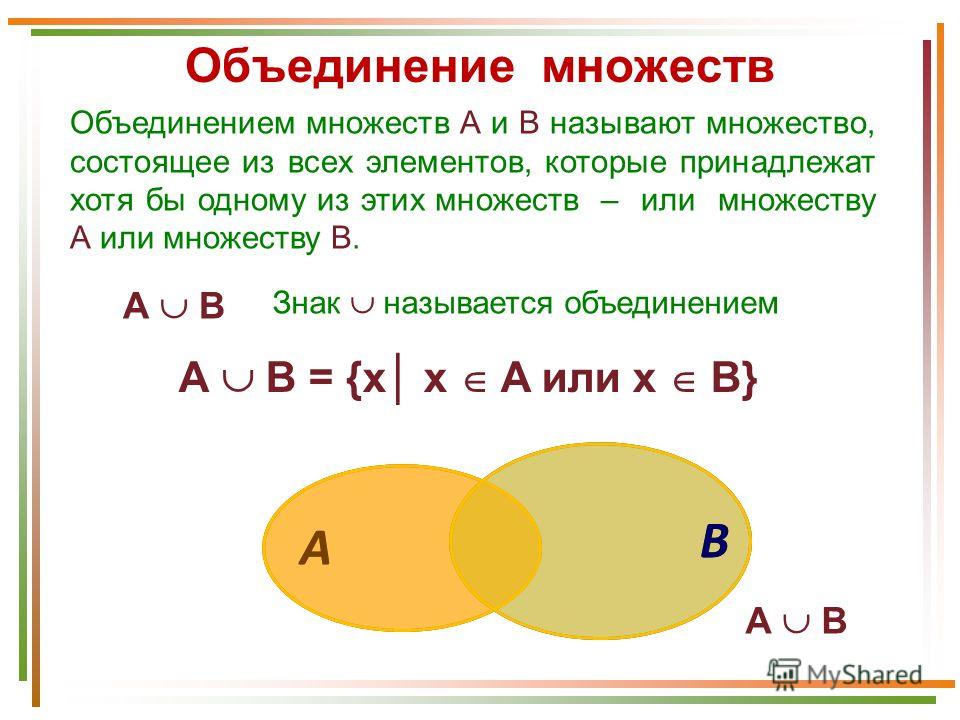 (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . 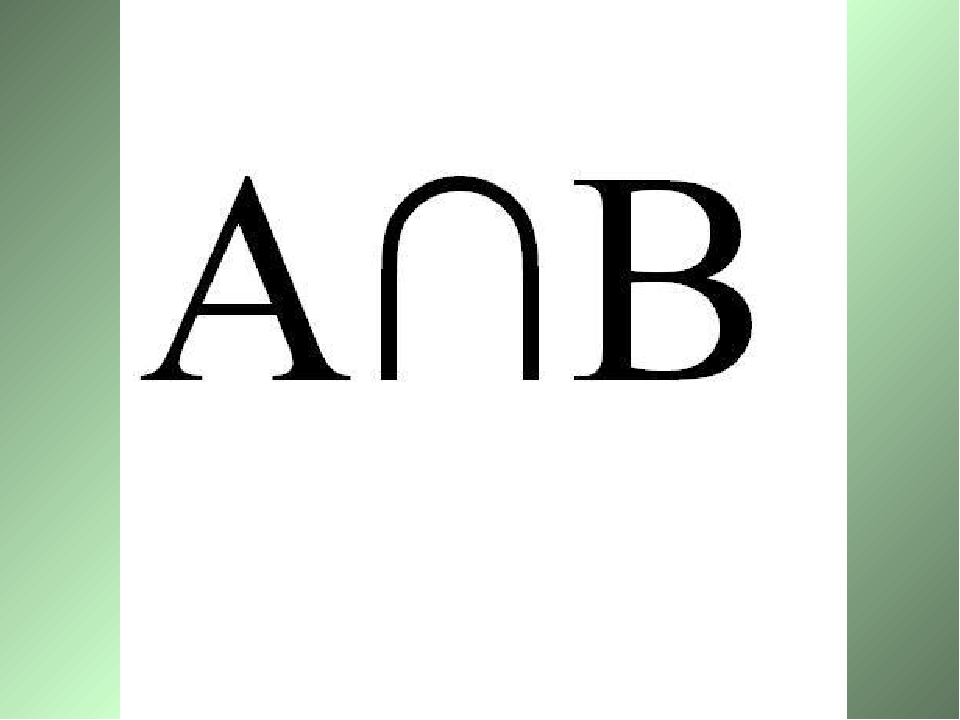 Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть .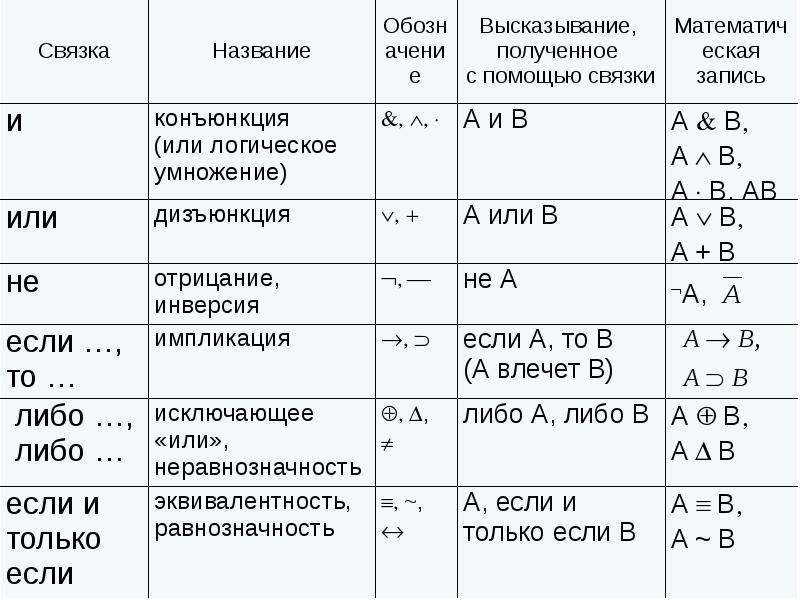 означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
.. Что такое Таблица математических символов?Некоторые символы математического языка — урок. Алгебра, 8 класс.
Натуральные числа — это числа, используемые для счёта предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
ℕ — обозначение множества всех натуральных чисел.ℤ — множество целых чисел. Оно состоит из натуральных чисел, им противоположных и нуля.
Пример:
\(…, -3, -2, -1, 0, 1, 2, 3, …\)
ℚ — множество рациональных чисел.
Оно получается из множества целых чисел, если к ним добавить обыкновенные дроби: 13,5152,−85….
Множество ℚ рациональных чисел — это множество, состоящее из чисел вида mn;−mn (где \(m\), \(n\) — натуральные числа) и числа \(0\).
Очевидно, ℕ — составной компонент множества ℤ, а ℤ — составной компонент множества ℚ. Обозначается это так: ℕ⊂ℤ;ℤ⊂ℚ.
⊂ — знак включения.
Запись x∈X показывает, что \(x\) — элемент множества \(X\).
Запись A⊂B показывает, что множество \(A\) — часть множества \(B\). Говорят: \(A\) — подмножество множества \(B\).
Для записи, что элемент \(x\) не принадлежит множеству \(X\) или что множество \(A\) не является подмножеством множества \(B\), используют символы принадлежности, перечёркнутые чертой: x∉X,A⊄B.
Данные математические символы используют для компактной записи верных математических утверждений, называемых истинными высказываниями.
Пример:
7∈ℕ;7∈ℤ;7∈ℚ;−5∉ℕ;ℕ⊂ℚ;ℤ⊄ℕ;2∈1;6;1;3⊂−2;8.
Каждое рациональное число может быть записано десятичной дробью (конечной или бесконечной периодической):
722=0,3181818…=0,3(18);4=4,000…=4,(0);7,3777=7,37770000…=7,3777(0).
Обратное утверждение также верно: каждую бесконечную десятичную периодическую дробь можно записать обыкновенной дробью. Следовательно, любая бесконечная десятичная периодическая дробь является рациональным числом.
Переведём бесконечную десятичную периодическую дробь 4,5(28) в обыкновенную дробь.
Пусть \(x=\) 4,5(28), т. е. \(x=\) 4,5282828… и т.д.
Сначала нужно передвинуть запятую, чтобы она стояла перед периодом. Для этого число \(x\) умножим на \(10\). Получим 10x=45,282828… и т.д.
Теперь передвинем запятую так, чтобы она стояла после периода.
Для этого число \(x\) умножим на \(1000\). Получим 1000x=4528,282828… и т.д.
Вычтем из второго равенства первое равенство.
1000x=4528,282828…10x=45,282828…
990x=4483¯
Отсюда x=4483990=4523990.
Приведём примеры перевода бесконечной десятичной периодической дроби в обыкновенную в сокращённой записи.
Пример:
1,(23)=123−199=12299=12399;1,5(23)=1523−5990=1518990=1259495.
Таблица математических знаков (символов): значения, распечатать
Ниже представлена таблица с основными математическими символами и знаками: корень (√), больше (>), меньше (<), равенство (=) и др. Также приведено их краткое описание и примеры для лучшего понимания.
YYYY» data-time-format=»HH:mm» data-features=»["after_table_loaded_script"]» data-search-value=»» data-lightbox-img=»» data-head-rows-count=»1″ data-pagination-length=»50,100,All» data-auto-index=»off» data-searching-settings=»{"columnSearchPosition":"bottom","minChars":"0"}» data-lang=»default» data-override=»{"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default"}» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>знак
е. 4 плюс 3 равно 7</nobr>» data-order=»<nobr>7 = 4 + 3,</nobr><br><nobr>т.е. 4 плюс 3 равно 7</nobr>»>7 = 4 + 3,т.е. 4 плюс 3 равно 7
7 не равно 10
равно 0,36</nobr>» data-order=»<nobr>0,35765 ≈ 0,36,</nobr><br><nobr>0,35765 прибл. равно 0,36</nobr>»>0,35765 ≈ 0,36,0,35765 прибл. равно 0,36
15 больше 10
6 меньше 8
10 больше или равно 4
3 меньше или равно 7
7 : 2 = 3 (остаток 1)
» data-order=».»>.
1%</nobr>» data-order=»<nobr>1‰ = 1/1000 = 0.1%</nobr>»>1‰ = 1/1000 = 0.1%microexcel.ru
Обозначения и соглашения — Уроки для приматов
Базовые математические символы
Кванторы:
- — квантор общности. Имеет значения «любой», «для любого», «каждый», «для каждого», «все», «для всех».
- — квантор существования. Имеет значения «существует», «существует не меньше одного». Иногда к квантору существования приписывается восклицательный знак (то есть квантор принимает вид ), и тогда полученное обозначение получает смысл «существует только один», «существует единственный».
Логические символы:
- — импликация.
Имеет значения «если… то…», «следовательно», «что влечёт». - — эквиваленция. Имеет значения «тогда, и только тогда, когда…», «что эквивалентно».
- — конъюнкция. Имеет значение «и». (то есть выражение является истинным тогда, и только тогда, когда истинными являются оба выражения и )
- — дизъюнкция. Имеет значение «или» в неисключающем смысле. (то есть выражение является истинным тогда, и только тогда, когда истинным является либо выражение , либо выражение , либо оба выражения)
Имеет значения «если… то…», «следовательно», «что влечёт».Обозначения, связанные с множествами:
- — фигурные скобки. Используются для обозначения множеств, состоящих из элементов, указанных/свойства которых указано внутри скобок.
Например, под выражением подразумевается множество, состоящее из элементов , и . - — символ принадлежности. Имеет значение «содержится в», «принадлежит», «находится в».
Например, (то есть содержится в множестве, которое состоит из элементов и ) является истинным высказыванием, а — ложным. - — символ отсутствия. Читается как символ принадлежности с приставкой «не».
Например, является ложным высказыванием, а — истинным. - , , , , — множества натуральных, целых, рациональных, вещественных и комплексных чисел соответственно.
- — отношение подмножества. Читается «содержится», «включено в».
Например, , поскольку все элементы первого множества ( и ) содержатся во втором множестве - — отношение подмножества, с допусканием равенства. Читается аналогично предыдущему. Имеет следующий смысл:
- — операция пересечения множеств.
- — операция объединения множеств.
- — операция декартова произведения множеств.
- — круглые и квадратные скобки. Зачастую используются для обозначения отрезков, интервалов и полуинтервалов во множестве вещественных чисел.
Например, полуинтервал содержит все вещественные числа между и , включая и не включая
Другие выражения и символы:
- — символ суммы с условиями. Как правило, условия суммирования описываются под символом суммы, а предел суммирования/номер последнего слагаемого — над ним.
Например, под выражением подразумевается сумма , а само выражение читается как «сумма по от до «. - — символ произведения с условиями. Условия накладываются аналогично символу суммы с условиями.
Например, под выражением подразумевается произведение . - — выражение со «счётчиком» , где — большее и меньшее соответственно целые числа либо бесконечность (со знаком плюс или минус). Под этим выражением подразумевается запись вида .
Например, под выражением подразумевается - — множество элементов , где — большее и меньшее соответственно целые числа либо бесконечность (со знаком плюс или минус). В случае, символ является бесконечностью, сама бесконечность в множество не входит. Иногда предыдущее выражение (в котором выражение уже не является множеством) заменяют записью вида либо либо .
- — верхний индекс над выражением . Подразумевает выражение « выполняется/верно по определению».
Как правило, условия суммирования описываются под символом суммы, а предел суммирования/номер последнего слагаемого — над ним.
Более подробно о математических символах можно прочитать здесь.
Поделиться ссылкой:
Установить членство и пустые наборы
Ниже приведен полный список кодов ALT Windows для математических символов: набор членства и пустых наборов , соответствующие им ссылки на числовые символы HTML-сущностей и, если они доступны, соответствующие им HTML-сущности с именами ссылок на символы и Кодовые точки Unicode.
Если вы плохо знакомы с кодами ALT и нуждаетесь в подробных инструкциях по использованию кодов ALT в документах Microsoft Office, таких как Word, Excel и Powerpoint, или в соответствующих программах и приложениях Microsoft Windows, прочтите, Как использовать коды ALT для ввода специальных символов. .
00″ data-percent-format=»10.00%» data-date-format=»DD.MM.YYYY» data-time-format=»HH:mm» data-features=»["after_table_loaded_script","import"]» data-search-value=»» data-head=»on» data-head-rows-count=»1″ data-pagination-length=»50,100,All» data-auto-index=»off» data-searching-settings=»{"columnSearchPosition":"bottom","minChars":"0"}» data-lang=»default» data-override=»{"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default"}» data-merged=»[]» data-responsive-mode=»0″ data-from-history=»0″> Дополнительные наборы математических символов см.
В разделе «Коды ALT для математических символов».
Полный список первых 256 кодов Windows ALT см. На странице Коды Windows ALT для специальных символов и символов.
Базовая математика | Нет | Обычно используемые математические символы, такие как> и < |
Греческие буквы | Строчные | Строчные буквы греческого алфавита |
Заглавные | Заглавные буквы греческого алфавита | |
Буквенные символы | Нет | Символы, похожие на буквы |
Операторы | Общие двоичные операторы | Символы, действующие на две величины, например + и ÷ |
Общие операторы отношения | Символы, которые выражают связь между двумя выражениями, например = и ~ | |
Базовые N-арные операторы | Операторы, работающие с рядом переменных или терминов | |
Продвинутые бинарные операторы | Дополнительные символы, действующие на две величины | |
Продвинутые операторы отношений | Дополнительные символы, которые выражают связь между двумя выражениями | |
Стрелки | Нет | Символы, указывающие направление |
Отношения отрицательные | Нет | Символы, выражающие отрицательную связь |
Скрипты | Скрипты | Гарнитура The Mathematical Script |
Фрактурс | Математический шрифт Fraktur | |
Двойной удар | Математический шрифт с двойным штрихом | |
Геометрия | Нет | Часто используемые геометрические символы |
Рекомендации по математике в журналах AIAA
Символика
Делайте уравнения простыми и избегайте необычных символов или символов.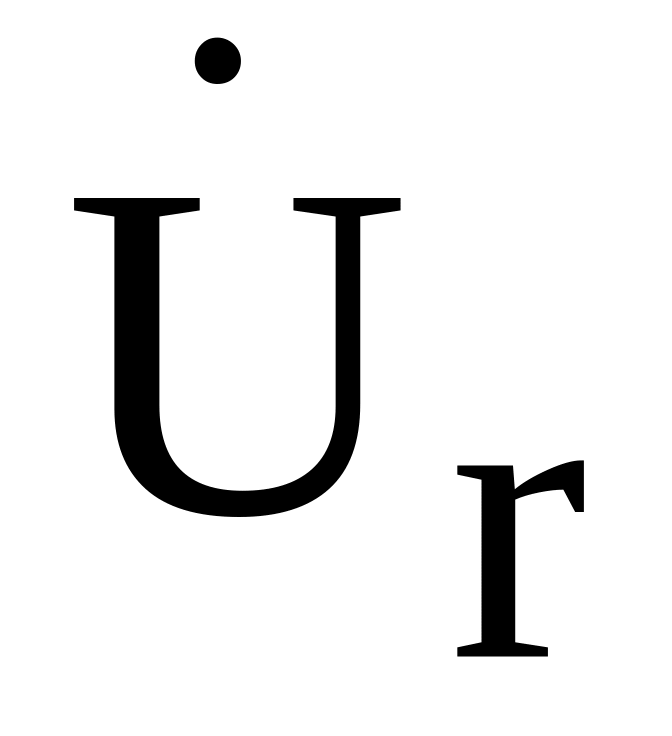
Используйте MathType или другое интерактивное программное обеспечение для редактирования формул, чтобы создавать свои уравнения, чтобы их можно было редактировать в процессе производства, если это необходимо. Не преобразовывайте свои уравнения в изображения. Чтобы ускорить процесс редактирования и составления, авторов просят соблюдать следующие условия:
- Избегайте использования символов с чертой чертой.
- Избегайте использования нескольких акцентов (более двух).
- В случае переменных, отмеченных чертой, обычно используется штриховой акцент ( ā ) для одной переменной и непрерывное правило ( abc ) для нескольких переменных.
- Пунктуация может использоваться для разделения математических выражений, отображаемых в одной строке, но в конце каждой строки (включая точки в конце уравнения) знаки пунктуации не используются.
Подстрочные и надстрочные индексы
Избегайте символов с несколькими уровнями подстрочных и надстрочных индексов.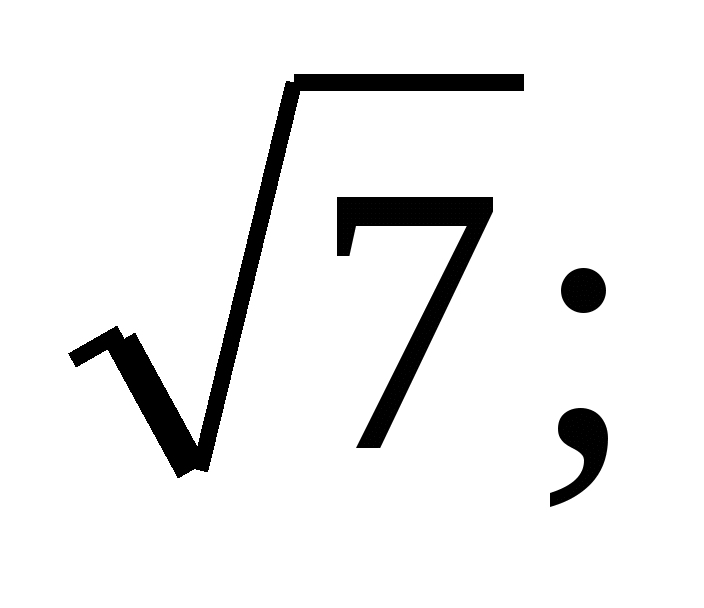
Лучше использовать в подстрочном индексе несколько символов, чем несколько слоев. Например, используйте X A1 вместо X A 1 .То же самое и с надстрочными индексами. В любом случае не следует использовать более двухуровневый нижний или верхний индекс.
Векторы
Если необходимо различать векторные и скалярные величины, используйте полужирный шрифт для векторных величин, а не столбцы или стрелки над символом. Жирный шрифт доступен для обычного, курсивного и греческого шрифтов.
Курсив против обычных символов
Используйте курсивный шрифт (наклонный) для всех переменных и констант, за некоторыми исключениями.Устанавливается обычным (вертикальным) шрифтом: sin, cos, tan, … и все аналогичные тригонометрические и гиперболические функции: log для десятичных логарифмов; такие качества, как мин., макс.,
opt, … и т.д .; и «d» для производной. Символы для описательных терминов устанавливаются обычным шрифтом, если они являются нижними или верхними индексами.
Акронимы, используемые в математических выражениях, также имеют обычный шрифт. «Ln» — натуральный логарифм.
будет задано в скрипте: (Ln)
Примечание. При использовании экспоненциального представления предпочтительна форма e xyz .Используйте форму exp [ x 2 + ( y — 1) — 3 + z ], когда показатели естественного основания необычно длинные или сложные, то есть содержат дроби, интегралы или сигма-суммирования.
Производные
Производные величины могут быть обозначены точкой или штрихом. X ‘ является предпочтительным и доступен до четвертой производной. Доступны одинарные / двойные точки.
Акценты
Семь общих математических акцентов можно автоматически поставить над любой курсивной, обычной или греческой буквой.Акценты не следует накладывать друг на друга. Эти акценты также можно использовать над немецкими буквами и буквами алфавита, но это приложение не
рекомендуемые.
Дроби
Чтобы уравнения были как можно более компактными, мелкие дроби обычно «разбиваются» в виде солидуса (/). Это особенно верно, если уравнение не содержит интегралов или сумм. Однако не смешивайте накопленные фракции и фракции. с солидом. Дроби с длинными числителями или знаменателями (пять или более символов) следует отображать и оставлять как построенные дроби для удобства чтения.
Радикалы
Знаки радикала произвольной длины доступны для использования над переменными (с надстрочным индексом или без него) и простыми дробями. Когда необходим радикал над переменной с диакритическими знаками или чертой, переменной с многоуровневыми надстрочными индексами или сложной дробью (где числитель или знаменатель содержит дробное, целое или сигма-суммирование), следует использовать экспоненциальное представление () 1/2 .
Многострочные уравнения
Длинные уравнения разбиваются на части и продолжаются для нескольких строк.
Момент, в котором такие уравнения должны быть нарушены, лучше всего определяется автором, чтобы разрывы удобно соответствовали выражаемой концепции. Эмпирическое правило относительно суммы, которая
помещается на одной строке в опубликованном журнале PDF-формат составляет 40 символов, занимающих горизонтальное пространство, включая все обычные символы, подстрочные и надстрочные индексы, круглые скобки, знаки плюс и минус и т. д.
Пример:
Знаки интеграла и суммирования каждый считается как три символа. Авторы должны отформатировать отдельные строки уравнений так, чтобы их ширина не превышала 40 символов, чтобы гарантировать, что они логически «разрываются» на печатной странице.Стиль AIAA требует, чтобы второй строка «ломаного» уравнения начинается со связующего математического знака; т.е.
Пронумеруйте каждое уравнение последовательно в скобках справа от уравнения или справа от последней строки «разорванного» уравнения. Группы уравнений, которые автор хочет отождествить с одним номером уравнения, предпочтительно должны быть индивидуальными.
пронумерованы (1a), (1b), (1c) и т. д. Исключением является матрица, в которой номер уравнения находится справа от средней точки матрицы.
Матрицы
Выровнять матрицы по центру по вертикали вокруг «главной линии» или средней точки каждой матрицы и отделить каждую строку в матрице пустой строкой.
Основы математической записи для машинного обучения
Последнее обновление 7 мая 2020 г.
Вы не можете избежать математических обозначений при чтении описаний методов машинного обучения.
Часто достаточно одного члена или одного фрагмента записи в уравнении, чтобы полностью разрушить ваше понимание всей процедуры.Это может быть очень неприятно, особенно для новичков в области машинного обучения из мира разработки.
Вы можете добиться больших успехов, если знаете несколько основных областей математической записи и некоторые приемы для работы с описанием методов машинного обучения в статьях и книгах.
В этом руководстве вы откроете для себя основы математической записи, с которыми вы можете столкнуться при чтении описаний методов машинного обучения.
После прохождения этого руководства вы будете знать:
- Обозначение для арифметики, включая вариации умножения, показателей, корней и логарифмов.
- Обозначение для последовательностей и наборов, включая индексацию, суммирование и членство в множестве.
- 5 Приемы, которые вы можете использовать, чтобы получить помощь, если вам не удается использовать математические обозначения.
Начните свой проект с моей новой книги «Линейная алгебра для машинного обучения», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.
Приступим.
- Обновление май / 2018 : Добавлены изображения для некоторых примечаний, чтобы сделать объяснения более понятными.
Основы математической записи для машинного обучения
Фото Кристиана Коллинза, некоторые права защищены.
Обзор учебного пособия
Это руководство разделено на 7 частей; их:
- Разочарование в математической нотации
- Арифметическая запись
- Греческий алфавит
- Обозначение последовательности
- Установить обозначение
- Другое обозначение
- Дополнительная справка
Есть ли другие области базовой математической записи, необходимые для машинного обучения, которые, по вашему мнению, я пропустил?
Дайте мне знать в комментариях ниже.
Нужна помощь с линейной алгеброй для машинного обучения?
Пройдите бесплатный 7-дневный ускоренный курс по электронной почте (с образцом кода).
Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.
Загрузите БЕСПЛАТНЫЙ мини-курс
Разочарование в математической нотации
Вы встретите математические обозначения, читая об алгоритмах машинного обучения.
Например, можно использовать обозначение:
- Опишите алгоритм.
- Опишите подготовку данных.
- Опишите результаты.
- Опишите испытательную привязь.
- Опишите последствия.
Эти описания могут быть в исследовательских статьях, учебниках, блогах и других местах.
Часто термины имеют четкое определение, но существуют также нормы математической записи, с которыми вы, возможно, не знакомы.
Достаточно одного члена или одного уравнения, которое вы не понимаете, и ваше понимание всего метода будет потеряно.
Я сам много раз страдал от этой проблемы, и это невероятно расстраивает!
В этом руководстве мы рассмотрим некоторые основные математические обозначения, которые помогут вам при чтении описаний методов машинного обучения.
Арифметическая запись
В этом разделе мы рассмотрим некоторые менее очевидные обозначения для базовой арифметики, а также несколько концепций, которые вы, возможно, забыли со школы.
Простая арифметика
Обозначения для основной арифметики такие, как вы бы ее написали.Например:
- Сложение: 1 + 1 = 2
- Вычитание: 2-1 = 1
- Умножение: 2 x 2 = 4
- Деление: 2/2 = 1
У большинства математических операций есть родственная операция, выполняющая обратную операцию; например, вычитание — это обратное сложение, а деление — обратное умножению.
Алгебра
Мы часто хотим описать операции абстрактно, чтобы отделить их от конкретных данных или конкретных реализаций.
По этой причине мы видим интенсивное использование алгебры: то есть прописные и / или строчные буквы или слова для представления терминов или понятий в математической нотации. Также часто используются буквы греческого алфавита.
Каждое подполе математики может иметь зарезервированные буквы: это термины или буквы, которые всегда означают одно и то же. Тем не менее, алгебраические термины должны быть определены как часть описания, и если это не так, это может быть просто плохим описанием, а не вашей ошибкой.
Обозначение умножения
Умножение — это обычное обозначение, у него несколько коротких рук.
Часто для обозначения умножения используется маленький «x» или звездочка «*»:
Вы можете увидеть, что используется точечная нотация; например:
Это то же самое, что:
В качестве альтернативы, вы можете не видеть никаких операций и разделения пробелов между ранее определенными терминами; например:
Что опять же одно и то же.
Показатели степени и квадратные корни
Показатель степени — это число в степени.
Обозначение записывается как исходное число или основание со вторым числом или показателем степени, показанным в виде верхнего индекса; например:
Что будет вычислено как 2, умноженное на себя 3 раза, или куб:
Число в степени 2 до называется его квадратом.
Квадрат числа можно инвертировать, вычислив квадратный корень. Это показано с использованием обозначения числа и с галочкой выше, я буду использовать здесь функцию «sqrt ()» для простоты.
Здесь мы знаем результат и показатель степени и хотим найти основание.
Фактически, операция корня может использоваться для инверсии любой экспоненты, просто так получилось, что квадратный корень по умолчанию предполагает показатель степени 2, представленный нижним индексом 2 перед отметкой квадратного корня.
Например, мы можем инвертировать вычисление числа, взяв кубический корень (обратите внимание, что 3 здесь не умножение, это запись перед галочкой в корне):
Логарифмы и е
Когда мы возводим 10 в целое число, мы часто называем это порядком величины.
Другой способ изменить эту операцию — вычислить логарифм результата 100, приняв за основу 10; в обозначениях это записывается как log10 ().
Здесь мы знаем результат и основание и хотим найти показатель степени.
Это позволяет нам очень легко перемещаться вверх и вниз по порядку величины. Логарифм в предположении, что основание 2 также широко используется, учитывая использование двоичной арифметики, используемой в компьютерах. Например:
Другой популярный логарифм — использовать натуральное основание e. Буква e зарезервирована и представляет собой специальное число или константу, называемую числом Эйлера (произносится как « oy-ler »), которое относится к значению с практически бесконечной точностью.
Возведение e в степень называется естественной экспоненциальной функцией:
Его можно инвертировать с помощью натурального логарифма, который обозначается как ln ():
Не вдаваясь в подробности, натуральный показатель степени и натуральный логарифм оказываются полезными во всей математике для абстрактного описания непрерывного роста некоторых систем, например.
грамм. системы, которые растут экспоненциально, например сложные проценты.
Греческий алфавит
греческих буквы используются в математических обозначениях переменных, констант, функций и т. Д.
Например, в статистике мы говорим о среднем, используя строчную греческую букву мю, а стандартное отклонение — как строчную греческую сигму. В линейной регрессии мы говорим о коэффициентах как о строчной букве бета. И так далее.
Полезно знать все прописные и строчные буквы греческого алфавита и знать, как их произносить.
Когда я был аспирантом, я напечатал греческий алфавит и приклеил его к монитору компьютера, чтобы запомнить. Полезный трюк!
Ниже представлен полный греческий алфавит.
Греческий алфавит, из Википедии
Страница Википедии под названием «Греческие буквы, используемые в математике, естествознании и инженерии» также является полезным руководством, поскольку на ней перечислены общие способы использования каждой греческой буквы в различных подполях математики и естествознания.
й элемент последовательности a.-й элемент последовательности b.
Последовательность операций
Математические операции могут выполняться над последовательностью.
Две операции выполняются с последовательностями так часто, что у них есть свои собственные сокращения: сумма и умножение.
Суммирование последовательностей
Сумма по последовательности обозначается прописной греческой буквой сигма. Он задается переменной и началом суммирования последовательности под сигмой (например, i = 1) и индексом конца суммирования над сигмой (например, i = 1).грамм. п).
Это сумма последовательности от элемента 1 до элемента n.
Умножение последовательности
Умножение над последовательностью обозначается прописной греческой буквой «пи». Он задается так же, как и суммирование последовательности с началом и концом операции под и над буквой соответственно.
Это произведение последовательности a, начиная с элемента 1, до элемента n.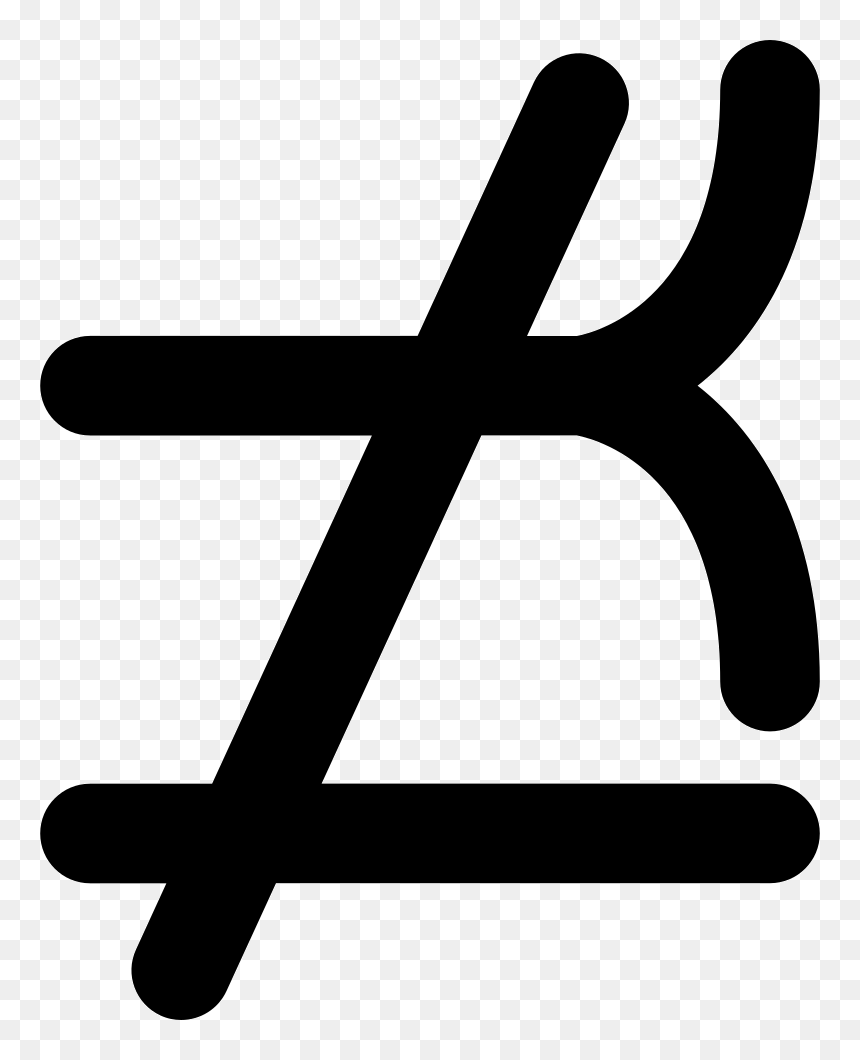
Установить обозначение
Набор — это группа уникальных предметов.
Мы можем видеть обозначение набора, используемое при определении терминов в машинном обучении.
Набор цифр
Обычный набор, который вы можете увидеть, представляет собой набор чисел, например, термин, определенный как находящийся в наборе целых чисел или наборе действительных чисел.
Некоторые общие наборы чисел, которые вы можете увидеть, включают:
- Набор всех натуральных чисел: N
- Набор всех целых чисел: Z
- Набор всех действительных чисел: R
Есть другие наборы; см. Специальные наборы в Википедии.
При определении терминов мы часто говорим о реальных значениях или действительных числах, а не о значениях с плавающей запятой, которые на самом деле являются дискретными творениями для операций в компьютерах.
Установить членство
Членство в множестве часто встречается в определениях терминов.
B
Узнайте больше о наборах в Википедии.
Другое обозначение
Есть и другие обозначения, с которыми вы можете столкнуться.
Кое-что из этого я пытаюсь изложить в этом разделе.
Обычно метод определяют в абстрактном виде, а затем снова определяют его как конкретную реализацию с отдельной нотацией.
Например, если мы оцениваем переменную x, мы можем представить ее, используя нотацию, изменяющую x; например:
Одна и та же нотация может иметь разное значение в другом контексте, например, для разных объектов или подполей математики.Например, часто путают | x |, что, в зависимости от контекста, может означать:
- | x |: Абсолютное или положительное значение x.
- | x |: длина вектора x.
- | x |: мощность множества x.
В этом руководстве были рассмотрены только основы математической записи. Есть некоторые подполи математики, которые больше подходят для машинного обучения, и их следует рассмотреть более подробно.
Их:
И, возможно, немного о многомерном анализе и теории информации.
Есть ли области математической записи, которые, по вашему мнению, отсутствуют в этом посте?
Дайте мне знать в комментариях ниже.
5 советов по работе с математическими обозначениями
В этом разделе перечислены некоторые советы, которые вы можете использовать, когда боретесь с математической записью в машинном обучении.
Подумайте об авторе
Люди написали статью или книгу, которую вы читаете.
Люди, которые могут ошибаться, делать упущения и даже сбивать с толку, потому что не до конца понимают, о чем пишут.
Немного ослабьте ограничения обозначений, которые вы читаете, и подумайте о намерениях автора. Что они пытаются донести?
Возможно, вы даже сможете связаться с автором по электронной почте, в Twitter, Facebook, LinkedIn и т. Д. И попросить разъяснений. Помните, что ученые хотят, чтобы другие люди понимали и использовали их работу (в основном).
Проверить Википедию
В Википедии есть списки обозначений, которые могут помочь сузить смысл или цель обозначений, которые вы читаете.
Я рекомендую вам начать с двух мест:
Эскиз в коде
Математические операции — это просто функции над данными.
Сопоставьте все, что вы читаете, с псевдокодом с переменными, циклами for и т. Д.
Возможно, вы захотите использовать язык сценариев в процессе работы вместе с небольшими массивами надуманных данных или даже электронной таблицей Excel.
По мере того, как ваше чтение и понимание техники улучшается, ваш код-набросок техники будет иметь больше смысла, и в конце у вас будет мини-прототип, с которым можно поиграть.
Я никогда особо не критиковал этот подход, пока не увидел академический набросок очень сложной статьи в нескольких строках MATLAB с некоторыми надуманными данными. Это сбило меня с толку, потому что я считал, что система должна быть полностью закодирована и работать с «реальным» набором данных, и что единственный вариант — получить исходный код и данные.
Я был очень неправ. Также, оглядываясь назад, парень был одарен.
Сейчас я использую этот метод все время и наброски на Python.
Искать альтернативы
Есть уловка, которую я использую, когда пытаюсь понять новую технику.
Я нахожу и читаю все статьи, в которых упоминается статья, которую я читаю, с использованием новой техники.
Чтение интерпретаций других ученых и повторных объяснений техники часто может прояснить мои недопонимания в исходном описании.
Но не всегда. Иногда это может замутить воду и ввести вводящие в заблуждение объяснения или новые обозначения. Но чаще всего это помогает. Вернувшись к исходной статье и перечитав ее, я часто нахожу случаи, когда в последующих статьях действительно были ошибки и неверное толкование исходного метода.
Задать вопрос
В Интернете есть места, где люди любят объяснять математику другим. Шутки в сторону!
Сделайте снимок экрана с обозначением, с которым вы боретесь, напишите полную ссылку или ссылку на него и разместите его и свою область непонимания на сайте вопросов и ответов.
Два отличных места для начала:
Каковы ваши приемы работы с математическими обозначениями?
Сообщите мне в комментариях ниже?
Дополнительная литература
Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.
Сводка
В этом руководстве вы открыли для себя основы математической записи, с которыми вы можете столкнуться при чтении описаний методов машинного обучения.
В частности, вы выучили:
- Обозначение для арифметики, включая вариации умножения, показателей, корней и логарифмов.
- Обозначение для последовательностей и наборов, включая индексацию, суммирование и членство в множестве.
- 5 Приемы, которые вы можете использовать, чтобы получить помощь, если вам не удается использовать математические обозначения.
Вы боретесь с математической записью?
Помогли ли какие-либо обозначения или советы в этом сообщении?
Дайте мне знать в комментариях ниже.
Познакомьтесь с линейной алгеброй для машинного обучения!
Развивайте рабочее понимание линейной алгебры
… путем написания строк кода на Python
Узнайте, как это сделать, в моей новой электронной книге:
Линейная алгебра для машинного обучения
Он предоставляет самоучителей по таким темам, как:
, векторные нормы, умножение матриц, тензоры, собственное разложение, SVD, PCA и многое другое…
И наконец разобраться в математике данных
Пропустить академики. Только результаты.
Посмотрите, что внутриСправка LaTeX
Что такое LaTeX?
LaTeX (произносится как LAH-tek) — это программа форматирования документов, которая является потомком TeX, изобретенной профессором Стэнфордского университета Дональдом Кнутом. Его цель — обеспечить высококачественное представление математических и других специализированных обозначений в виде шрифтов.
Большинство рефератов можно выполнить без дополнительных команд LaTeX, но если вам нужно использовать греческие буквы или большинство математических символов, это необходимо сделать с помощью LaTeX.
Наиболее часто используемые символы показаны ниже. Многие из них выполняются в «математическом режиме» и, следовательно, начинаются и заканчиваются знаком доллара ($).
Если вы используете несколько символов в математическом режиме, нужен только один $ перед всей строкой и один $ в конце строки; т.е. $ \ alpha H_ {2} O $.
«Зарезервированные» персонажи
Некоторые символы имеют в LaTeX особое значение. Если вы хотите включить один или несколько из этих символов в свой реферат, используйте соответствующую команду, приведенную ниже, для «выключения» специального значения.
Примечание: Не используйте «\ ~» для отображения символа, означающего «приблизительно».
Вместо этого используйте $ \ sim $. Например, «Число Пи равно $ \ sim $ 3,1416.
греческие буквы
Для правильного отображения все греческие буквы должны быть окружены знаками $, e.г., $ \ pi $. Обратите внимание, что omicron — это просто строчная буква «o».
Нижний регистр
| \ альфа | \ beta | \ гамма | \ дельта | \ эпсилон | \ zeta |
| \ theta | \ eta | \ iota | \ каппа | \ лямбда | мк |
| \ nu | \ xi | \ pi | \ rho | \ sigma | \ тау |
| \ ипсилон | \ phi | \ чи | \ фунт / кв. Дюйм | \ омега | |
Верхний корпус
| \ Гамма | \ Дельта | \ Theta | \ Лямбда | \ Си | \ Pi |
| \ Sigma | \ Ипсилон | \ Phi | \ фунтов на квадратный дюйм | \ Omega |
Надстрочные знаки
Надстрочная команда: $ ^ {надстрочные символы} $.
(каретка или «контроль») на большинстве клавиатур это сдвиг 6. Всякий раз, когда используется какая-либо команда, которая начинается с обратной косой черты (\), а знак доллара ($) не следует сразу за ней, за этой командой должен следовать пробел, чтобы очертить команду; следовательно, пробел после \ pi выше. Это пространство не появится в окончательном выводе; формула будет печататься непрерывно.
Индексы
Команда подстрочного индекса: $ _ {указываются символы} $.
Пример: формула для воды: H $ _ {2} $ O .
Примечание: Символ _ (подчеркивание) заменяется сдвигом — (дефис) на большинстве клавиатур. Знак доллара ($) показан здесь после H; он также может предшествовать этому.
Сноски
Сноски следует создавать с помощью команды сноски, а не вручную создавать их с надстрочными индексами.
Пример: LUNA послужила источником нескольких успешных исследований критических реакций в pp-цепях.
\ footnote {Дж. Доу, \ textbf {Phy. Ред.} 161, 1500}
Это сгенерирует автоматически пронумерованную сноску, где находится команда, а также поместит текст сноски внизу страницы.{\ circ} долл. США
Примечание: Знак доллара ($) также может стоять перед 45.
Ангстрем
Команда для ангстрема: {\ AA}
Символы, используемые на языках, отличных от английского
Команды для следующих символов НЕ выполняются в математическом режиме и поэтому НЕ должны быть окружены знаками доллара.
Примечание: В приведенной ниже таблице буквы c и o используются для демонстрации расстановки ударений и диакритических знаков над любой буквой.{o}
o
Дополнительные ресурсы по LaTeX
Полная информация о символах LaTeX, названиях разметки, книгах, руководствах, часто задаваемых вопросах и группах обсуждения доступна на веб-сайте TeX Users Group (TUG) по адресу www.
tug.org.
Получение помощи
Если у вас возникнут проблемы на любом этапе запроса, генерации или отправки тезисов, обратитесь в службу поддержки APS по тезисам, отправив электронное письмо по адресу [email protected] или позвонив в службу поддержки Abs-Help по адресу 301-209-3290 в рабочее время по восточному времени.
Список символов — Дискретная математика [Книга]
Список символов
| Символ | Значение |
|---|---|
Глава первая | |
∈ | принадлежит, является элементом |
{a, b} | набор, состоящий из a и b |
∉ | не принадлежит, не является элементом |
R | набор действительных чисел |
Z | набор целых чисел |
Z + | набор натуральных чисел |
№ | набор натуральных чисел |
ɸ | пустой набор, пустой набор, недействительный набор |
⊆ | набор включения, является подмножеством |
не является подмножеством | |
⇔ | тогда и только тогда, когда |
P (A) | набор мощности набора A, набор всех подмножеств набора A |
| A | | количество элементов в множестве A, мощность конечного множества A |
U | универсальный набор, вселенная дискурса |
∪ | штуцер комплектов |
∩ | пересечение множеств |
Б — А | относительное дополнение. |
..Получите по дискретной математике сейчас с онлайн-обучением O’Reilly.
участника O’Reilly проходят онлайн-обучение в режиме реального времени, а также получают книги, видео и цифровой контент от 200+ издателей.
Добро пожаловать в NAM!
Миссия, цель и задачи ДННациональная ассоциация математиков (NAM) — это некоммерческая профессиональная организация в области математических наук, членство в которой открыто для всех лиц, заинтересованных в миссии и целях NAM, а именно:
- продвижение передового опыта в математических науках и
- способствует математическому развитию всех недопредставленных меньшинств.
NAM была основана в 1969 году; в 2019 году нам исполнилось 50 лет. Миссия и связанные с ней цели приводят к следующим конкретным основным целям ДН.
- Для участия в мероприятиях, проектах, программах, конференциях, семинарах, семинарах и т. Д., Которые призваны вдохновлять, мотивировать, продвигать и помогать людям всех возрастов искать, начинать или поддерживать активную заинтересованность / карьеру в какой-либо области (s) математических наук.
- Поощрять и помогать в постоянном профессиональном развитии практикующих ученых-математиков и преподавателей, особенно тех групп, которые недопредставлены в математических науках.
- Поддерживать постоянное совершенствование преподавания и совершенствования учебных программ по математическим наукам, особенно в колледжах и университетах / институтах для исторических чернокожих.
- Пропаганда, продвижение и поддержка исследований в области математических наук, особенно для недопредставленных меньшинств.
- Повысить осведомленность сообщества математиков и широкой общественности о важных вопросах в областях математических наук, особенно о тех, которые представляют большой интерес для недопредставленных меньшинств.
Д., Которые призваны вдохновлять, мотивировать, продвигать и помогать людям всех возрастов искать, начинать или поддерживать активную заинтересованность / карьеру в какой-либо области (s) математических наук. Хотя членство открыто для всех, NAM стремится продвигать передовые достижения в математических науках для недопредставленных американских меньшинств в целом и афроамериканцев в частности.
У нас более 500 участников, и мы надеемся, что вы присоединитесь и станете одним из них!
Приветственное заявление NAM
Национальная ассоциация математиков (NAM) — это некоммерческая профессиональная организация в области математических наук, членство в которой открыто для всех лиц, заинтересованных в миссии и целях NAM, которые способствуют совершенствованию математических наук и способствуют математическому развитию всех. недопредставленные меньшинства.NAM был основан на принципах включения и разнообразия в то время, когда крупные американские математические организации исключали цветных математиков из своих членов, редакционных советов, исследовательских симпозиумов и другой профессиональной деятельности. Откровенное человеческое неуважение, домогательства или нападение — сексуального или иного характера — являются формами неправомерного поведения, которые подрывают целостность NAM: такое неправомерное поведение недопустимо внутри организации или в деятельности NAM.
ДН продолжает приветствовать и поощрять разнообразие в выражении научных идей и свободу самовыражения.ДН стремится продвигать равные возможности и обращение для всех членов ДН и участников мероприятий, спонсируемых ДН, независимо от пола, гендерной идентичности или выражения, расы, цвета кожи, национального или этнического происхождения, религии или религиозных убеждений, возраста, семейного положения. , сексуальная ориентация, инвалидность, статус ветерана или любая другая причина, не имеющая отношения к научным достижениям.
Выражение признательности: В качестве основы для этого утверждения были взяты принципы, принятые Ассоциацией женщин-математиков (AWM) и Национальным научным фондом (NSF).
NAM имеет Совет директоров, а также двенадцать постоянных комитетов. Мы проводим мероприятия на совместных встречах по математике, а также на MathFest МАА. В целом, NAM имеет двенадцать фирменных мероприятий, которые проходят в пяти точках в течение года:
Вы можете узнать больше о предстоящих программах и мероприятиях NAM, щелкнув здесь.