Из истории математических символов. — математика, уроки
Из истории математических символов.
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
Математика – это первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число 35 в виде нарисованных в ряд 35 палочек. Можно сказать, что 1 палочка – это первый математический символ.
Слово математика пришло к нам из древнегреческого, где μάθημα означало «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю.
Математическая «письменность», которую мы сейчас используем — от обозначений неизвестных буквами x, y, z до знака интеграла — складывалась постепенно. Развитие символики упрощало работу с математическими операциями и способствовало развитию самой математики.
С древнегреческого «символ» (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию.
С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение.
Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.
Знаки сложения, вычитания
История математических обозначений начинается с палеолита. Этим временем датируются камни и кости с насечками, использовавшимися для счета. Наиболее известный пример — кость Ишанго. Знаменитая кость из Ишанго (Конго) датируемая примерно 20 тысяч лет до новой эры, доказывает, что уже в то время человек выполнял достаточно сложные математические операции. Насечки на кости использовались для сложения и наносились группами, символизируя сложения чисел.
В Древнем Египте была уже намного более продвинутая система обозначений. Например, в папирусе Ахмеса в качестве символа сложения используется изображение двух ног, идущих вперед по тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полуэллиптическую кривую для вычитания.
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. Происхождение этих символов неясно. Одна из версий — они ранее использовались в торговом деле как признаки прибыли и убытка.
Считается, так же, что наш знак происходит от одной из форм слова “et’’, которое по-латыни значит “и’’. Выражение a + b писалось на латыни так: a et b. Постепенно, из-за частого использования, от знака «et» осталось только » t » , которое, со временем превратилось в » + «. Первым человеком, который, возможно, использовал знак как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.
Обозначения вычитания были более запутанными, так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
Первое использование современного алгебраического знака “” относится к немецкой рукописи по алгебре 1481 г., которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: « » и « — » . Систематическое использование знаков « » и « — » для сложения и вычитания встречается у Иоганна Видмана. Немецкий математик Иоганн Видманн (1462-1498) первым использовал оба знака для пометок присутствия и отсутствия студентов на своих лекциях.
Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ. Видман сам ввел его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест « † », иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид « ».
Знак равенства
Знак равенства в математике и других точных науках пишут между двумя идентичными по своему размеру выражениями.
Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный). В античной и средневековой математике равенство обозначалось словесно, например, est egale, или использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые буквы слова “равный’’, но это не было общепринятым. Знак равенства «=» ввел в 1557 году уэльский врач и математик Роберт Рекорд (Recorde R., 1510-1558). Математическим символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя одинаковыми горизонтальными параллельными отрезками, гораздо более длинными, чем те, что используются сегодня. Английский математик Роберт Рекорд был первым, кто начал использовать символ «равенство», аргументируя словами: «никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». Но ещё в XVII веке Рене Декарт использовал аббревиатуру “ae’’. Франсуа Виет знаком равенства обозначал вычитание.
Родственные символы для обозначения приблизительного равенства «≈» и тождества «≡» являются совсем молодыми — первый введен в 1885 году Гюнтером, второй — в 1857 году Риманом
Знаки умножения и деления
Знак умножения в виде крестика («х») ввел англиканский священник-математик Уильям Отред в 1631 году. До него для знака умножения использовали букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон, 1634), звёздочка (Иоганн Ран, 1659).
Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Знак процента.
Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта (1685). В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%».
Так из-за опечатки этот знак вошёл в обиход.
Знак бесконечности
Нынешний символ бесконечности «∞» ввел в употребление Джон Уоллис в 1655 году. Джон Уоллис издал большой трактат «Арифметика бесконечного» (лат. Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque Difficiliora Matheseos Problemata), где ввёл придуманный им символ бесконечности. До сих пор так и не известно, почему он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных гипотез связывает происхождение этого символа с латинской буквой «М», которую римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента) математиком Бернулли приблизительно сорок лет спустя.
Другая версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия «бесконечность»: движение без конца. По линиям числа 8 можно совершать, как по велотреку, бесконечное движение.
Для того, чтобы не путать введенный знак с числом 8, математики решили располагать его горизонтально. Получилось . Такое обозначение cтало стандартным для всей математики, не только алгебры. Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не поворачивай — она не изменится. Поэтому выбор и пал именно на 8.
Другой вариант — змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца.
Многие считают, что лист Мёбиуса является прародителем символа бесконечности, т.к символ бесконечности был запатентован после изобретения устройства «лента Мебиуса» (названный в честь математика девятнадцатого столетия Мебиуса). Лента Мебиуса — полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Однако по имеющимся историческим сведениям символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса
Знаки угла и перпендикулярности
Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон.
Символ перпендикулярности у него был перевёрнут, напоминая букву T. Символ угла напоминал значок , современную форму ему придал Уильям Отред (1657).
Знак параллельности
Символ «параллельности» известен с античных времён, его использовали Герон и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально (Отред (1677), Керси (John Kersey) и др. математики XVII века).
Число ПИ
Общепринятое обозначение числа, равного отношению длины окружности к ее диаметру (3,1415926535…), впервые образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια —окружность и περίμετρος — периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.
Синус и косинус
Интересно появление синуса и косинуса.
Sinus с латинского — пазуха, впадина. Но история у такого названия долгая. Далеко в тригонометрии продвинулись индийские математики в районе 5 века. Самого слова «тригонометрия» не было, оно было введено Георгом Клюгелем в 1770 году.) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для краткости называли просто — джия (тетива). Когда арабы переводили работы индусов с санскрита, они не стали переводить «тетиву» на арабский, а просто транскрибировали слово арабскими буквами. Получилась джиба. Но так как в слоговой арабской письменности краткие гласные не обозначаются, то реально остается дж-б, что похоже на другое арабское слово — джайб (впадина, пазуха). Когда Герард Кремонский в 12 веке переводил арабов на латынь, он перевел это слово как sinus, что по-латыни также означает пазуху, углубление.
Косинус появился автоматически, т.к. индусы называли его коти-джия, или сокращено ко-джия.
Коти — изогнутый конец лука на санскрите. Современные краткие обозначения и введены Уильямом Отредом и закреплены в трудах Эйлера.
Обозначения тангенса/котангенса имеют намного более позднее происхождение (английское слово tangent происходит от латинского tangere — касаться). И даже до сих пор нет унифицированного обозначения — в одних странах чаще используется обозначение tan, в других — tg
Сокращение «Что и требовалось доказать» (ч.т.д.)
«Quod erat demonstrandum» (квол эрат лэмонстранлум).
Греческая фраза имеет значение «что требовалось доказывать», а латинская — «что нужно было показать». Этой формулой заканчивается каждое математическое рассуждение великого греческого математика Древней Греции Эвклида (III в. до н. э.). В переводе с латинского — что и требовалось доказать. В средневековых научных трактатах эту формулу писали часто в сокращенном виде: QED.
Математические обозначения.
Символы | История символов |
+ — | Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии. |
× ∙ | Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. |
/ : ÷ | Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века. |
= | Знак равенства предложил Роберт Рекорд (1510—1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем. |
Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. | |
% | Символ процента появляется в середине XVII века сразу в нескольких источниках, его происхождение неясно. Есть гипотеза, что он возник от ошибки наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более вероятно, что это скорописный коммерческий значок, возникший лет на 100 раньше. |
√ | Знак корня впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы слова radix (корень). Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня. |
an | Возведение в степень. |
( ) | Скобки появились у Тартальи (1556) для подкоренного выражения, но большинство математиков предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц. |
Σ | Знак суммы ввёл Эйлер в 1755 году |
П | Знак произведения ввёл Гаусс в 1812 году |
i | Букву i как код мнимой единицы: предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый). |
π | Общепринятое обозначение числа 3.14159… образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр, то есть длина окружности. |
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). | |
y’ | Краткое обозначение производной штрихом восходит к Лагранжу. |
Символ предела появился в 1787 году у Симона Люилье (1750—1840). | |
Символ бесконечности придумал Валлис, опубликован в 1655 году. |
До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
До него писали словами: больше, меньше.
Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676).
Математическая наука необходима для цивилизованного общества.
Математика содержится во всех науках. Математический язык смешивается с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые создают новые технологии. Сохранившиеся открытия дают возможность решать сложные математически задачи. И древний математический язык нам понятен, а открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли физические законы. Мы изучаем их в школе. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение математики необходимо для новых открытий.
Литература.
Рыбников К.А. История математики. Издательство Московского Университета, 1974
Интернет.
www математические символы.
7
Откуда взялись математические символы | Образовательная социальная сеть
li:before{content:»\002022 «}#doc8312611 .lst-kix_list_14-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_14-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_14-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_14-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_14-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_14-6>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_9-3{list-style-type:none}#doc8312611 ul.lst-kix_list_9-4{list-style-type:none}#doc8312611 ul.lst-kix_list_9-1{list-style-type:none}#doc8312611 ul.lst-kix_list_9-2{list-style-type:none}#doc8312611 ul.lst-kix_list_9-7{list-style-type:none}#doc8312611 ul.lst-kix_list_9-8{list-style-type:none}#doc8312611 ol.lst-kix_list_20-2.start{counter-reset:lst-ctn-kix_list_20-2 0}#doc8312611 ul.lst-kix_list_9-5{list-style-type:none}#doc8312611 ul.lst-kix_list_9-6{list-style-type:none}#doc8312611 ul.
lst-kix_list_9-0{list-style-type:none}#doc8312611 .lst-kix_list_14-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_20-7>li{counter-increment:lst-ctn-kix_list_20-7}#doc8312611 ul.lst-kix_list_17-1{list-style-type:none}#doc8312611 ul.lst-kix_list_17-0{list-style-type:none}#doc8312611 ol.lst-kix_list_28-3.start{counter-reset:lst-ctn-kix_list_28-3 0}#doc8312611 ul.lst-kix_list_17-8{list-style-type:none}#doc8312611 ul.lst-kix_list_17-7{list-style-type:none}#doc8312611 ul.lst-kix_list_17-6{list-style-type:none}#doc8312611 ul.lst-kix_list_17-5{list-style-type:none}#doc8312611 .lst-kix_list_28-7>li{counter-increment:lst-ctn-kix_list_28-7}#doc8312611 ul.lst-kix_list_17-4{list-style-type:none}#doc8312611 ul.lst-kix_list_17-3{list-style-type:none}#doc8312611 .lst-kix_list_14-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_17-2{list-style-type:none}#doc8312611 .lst-kix_list_5-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_24-7>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_24-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_24-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_8-4{list-style-type:none}#doc8312611 ul.lst-kix_list_8-5{list-style-type:none}#doc8312611 ol.lst-kix_list_20-7.start{counter-reset:lst-ctn-kix_list_20-7 0}#doc8312611 .lst-kix_list_5-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_8-2{list-style-type:none}#doc8312611 ul.lst-kix_list_8-3{list-style-type:none}#doc8312611 ul.lst-kix_list_8-8{list-style-type:none}#doc8312611 .lst-kix_list_24-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_8-6{list-style-type:none}#doc8312611 .lst-kix_list_24-4>li:before{content:»\002022 «}#doc8312611 ul.
lst-kix_list_8-7{list-style-type:none}#doc8312611 .lst-kix_list_24-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_5-5>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_8-0{list-style-type:none}#doc8312611 ul.lst-kix_list_8-1{list-style-type:none}#doc8312611 .lst-kix_list_24-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_23-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-3>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-6{list-style-type:none}#doc8312611 ol.lst-kix_list_27-5{list-style-type:none}#doc8312611 ol.lst-kix_list_27-8{list-style-type:none}#doc8312611 .lst-kix_list_23-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_23-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-4>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-7{list-style-type:none}#doc8312611 ol.
lst-kix_list_27-2{list-style-type:none}#doc8312611 .lst-kix_list_23-2>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_16-2{list-style-type:none}#doc8312611 ol.lst-kix_list_27-1{list-style-type:none}#doc8312611 ul.lst-kix_list_16-1{list-style-type:none}#doc8312611 ol.lst-kix_list_27-4{list-style-type:none}#doc8312611 ul.lst-kix_list_16-0{list-style-type:none}#doc8312611 ol.lst-kix_list_27-3{list-style-type:none}#doc8312611 .lst-kix_list_23-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_23-8>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-0{list-style-type:none}#doc8312611 .lst-kix_list_23-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_24-1>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_16-8{list-style-type:none}#doc8312611 ul.lst-kix_list_16-7{list-style-type:none}#doc8312611 ul.lst-kix_list_16-6{list-style-type:none}#doc8312611 ul.lst-kix_list_16-5{list-style-type:none}#doc8312611 .
lst-kix_list_24-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_16-4{list-style-type:none}#doc8312611 .lst-kix_list_6-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_16-3{list-style-type:none}#doc8312611 .lst-kix_list_6-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_23-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_23-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_6-6>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-6.start{counter-reset:lst-ctn-kix_list_27-6 0}#doc8312611 .lst-kix_list_7-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_7-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_22-2>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_22-6>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_7-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-2>li{counter-increment:lst-ctn-kix_list_27-2}#doc8312611 .lst-kix_list_22-0>li:before{content:»\0025cf «}#doc8312611 .
lst-kix_list_22-8>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_13-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_7-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_22-4>li:before{content:»o «}#doc8312611 .lst-kix_list_15-5>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_28-8{list-style-type:none}#doc8312611 ol.lst-kix_list_28-5{list-style-type:none}#doc8312611 ol.lst-kix_list_28-4{list-style-type:none}#doc8312611 .lst-kix_list_27-3>li{counter-increment:lst-ctn-kix_list_27-3}#doc8312611 ol.lst-kix_list_28-7{list-style-type:none}#doc8312611 ol.lst-kix_list_28-6{list-style-type:none}#doc8312611 ol.lst-kix_list_28-1{list-style-type:none}#doc8312611 ol.lst-kix_list_28-0{list-style-type:none}#doc8312611 .lst-kix_list_4-1>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_28-3{list-style-type:none}#doc8312611 ol.lst-kix_list_28-2{list-style-type:none}#doc8312611 .lst-kix_list_15-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_19-7{list-style-type:none}#doc8312611 ul.
lst-kix_list_19-6{list-style-type:none}#doc8312611 .lst-kix_list_4-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_4-5>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_19-5{list-style-type:none}#doc8312611 ul.lst-kix_list_19-4{list-style-type:none}#doc8312611 ul.lst-kix_list_19-3{list-style-type:none}#doc8312611 .lst-kix_list_25-5>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_19-2{list-style-type:none}#doc8312611 ul.lst-kix_list_19-1{list-style-type:none}#doc8312611 ul.lst-kix_list_19-0{list-style-type:none}#doc8312611 .lst-kix_list_15-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_25-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_15-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_19-8{list-style-type:none}#doc8312611 ol.lst-kix_list_27-4.start{counter-reset:lst-ctn-kix_list_27-4 0}#doc8312611 .lst-kix_list_20-0>li{counter-increment:lst-ctn-kix_list_20-0}#doc8312611 .lst-kix_list_12-3>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_12-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_13-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_18-0{list-style-type:none}#doc8312611 .lst-kix_list_28-0>li{counter-increment:lst-ctn-kix_list_28-0}#doc8312611 .lst-kix_list_13-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_12-5>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_28-8.start{counter-reset:lst-ctn-kix_list_28-8 0}#doc8312611 ul.lst-kix_list_18-8{list-style-type:none}#doc8312611 ul.lst-kix_list_18-7{list-style-type:none}#doc8312611 ul.lst-kix_list_18-6{list-style-type:none}#doc8312611 ul.lst-kix_list_18-5{list-style-type:none}#doc8312611 .lst-kix_list_12-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_18-4{list-style-type:none}#doc8312611 ul.lst-kix_list_18-3{list-style-type:none}#doc8312611 ul.lst-kix_list_18-2{list-style-type:none}#doc8312611 ul.lst-kix_list_18-1{list-style-type:none}#doc8312611 .lst-kix_list_13-1>li:before{content:»\002022 «}#doc8312611 ul.
lst-kix_list_24-0{list-style-type:none}#doc8312611 ul.lst-kix_list_24-1{list-style-type:none}#doc8312611 ul.lst-kix_list_24-2{list-style-type:none}#doc8312611 ul.lst-kix_list_24-3{list-style-type:none}#doc8312611 ul.lst-kix_list_24-4{list-style-type:none}#doc8312611 ul.lst-kix_list_24-5{list-style-type:none}#doc8312611 .lst-kix_list_28-8>li{counter-increment:lst-ctn-kix_list_28-8}#doc8312611 .lst-kix_list_3-0>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_20-5.start{counter-reset:lst-ctn-kix_list_20-5 0}#doc8312611 ul.lst-kix_list_5-7{list-style-type:none}#doc8312611 ul.lst-kix_list_5-8{list-style-type:none}#doc8312611 ul.lst-kix_list_5-5{list-style-type:none}#doc8312611 ul.lst-kix_list_5-6{list-style-type:none}#doc8312611 .lst-kix_list_21-8>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_26-5>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_24-6{list-style-type:none}#doc8312611 ul.lst-kix_list_5-0{list-style-type:none}#doc8312611 ul.lst-kix_list_24-7{list-style-type:none}#doc8312611 .
lst-kix_list_3-4>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_24-8{list-style-type:none}#doc8312611 ul.lst-kix_list_5-3{list-style-type:none}#doc8312611 .lst-kix_list_3-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_5-4{list-style-type:none}#doc8312611 .lst-kix_list_26-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_5-1{list-style-type:none}#doc8312611 .lst-kix_list_8-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_5-2{list-style-type:none}#doc8312611 .lst-kix_list_8-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_3-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_21-0>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_26-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_21-1>li:before{content:»o «}#doc8312611 .lst-kix_list_8-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_13-5{list-style-type:none}#doc8312611 ul.lst-kix_list_13-4{list-style-type:none}#doc8312611 ul.lst-kix_list_13-3{list-style-type:none}#doc8312611 ul.
lst-kix_list_13-2{list-style-type:none}#doc8312611 ul.lst-kix_list_13-1{list-style-type:none}#doc8312611 .lst-kix_list_3-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_13-0{list-style-type:none}#doc8312611 .lst-kix_list_26-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_8-4>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_13-8{list-style-type:none}#doc8312611 .lst-kix_list_11-1>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_13-7{list-style-type:none}#doc8312611 ul.lst-kix_list_13-6{list-style-type:none}#doc8312611 .lst-kix_list_21-5>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_21-4>li:before{content:»o «}#doc8312611 .lst-kix_list_11-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_26-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_8-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_16-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_23-0{list-style-type:none}#doc8312611 ul.lst-kix_list_23-1{list-style-type:none}#doc8312611 .
lst-kix_list_16-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_23-2{list-style-type:none}#doc8312611 ul.lst-kix_list_23-3{list-style-type:none}#doc8312611 ul.lst-kix_list_23-4{list-style-type:none}#doc8312611 ul.lst-kix_list_23-5{list-style-type:none}#doc8312611 ul.lst-kix_list_23-6{list-style-type:none}#doc8312611 .lst-kix_list_4-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_4-7>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_20-0.start{counter-reset:lst-ctn-kix_list_20-0 0}#doc8312611 .lst-kix_list_17-0>li:before{content:»\0025cf «}#doc8312611 ul.lst-kix_list_4-8{list-style-type:none}#doc8312611 .lst-kix_list_16-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_4-6{list-style-type:none}#doc8312611 ul.lst-kix_list_4-7{list-style-type:none}#doc8312611 ol.lst-kix_list_27-8.start{counter-reset:lst-ctn-kix_list_27-8 0}#doc8312611 .lst-kix_list_25-1>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_4-0{list-style-type:none}#doc8312611 ul.
lst-kix_list_23-7{list-style-type:none}#doc8312611 .lst-kix_list_25-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_16-4>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_4-1{list-style-type:none}#doc8312611 ul.lst-kix_list_23-8{list-style-type:none}#doc8312611 .lst-kix_list_16-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_4-4{list-style-type:none}#doc8312611 ul.lst-kix_list_4-5{list-style-type:none}#doc8312611 ul.lst-kix_list_4-2{list-style-type:none}#doc8312611 ul.lst-kix_list_4-3{list-style-type:none}#doc8312611 ul.lst-kix_list_12-6{list-style-type:none}#doc8312611 ul.lst-kix_list_12-5{list-style-type:none}#doc8312611 .lst-kix_list_17-7>li:before{content:»o «}#doc8312611 ul.lst-kix_list_12-4{list-style-type:none}#doc8312611 ul.lst-kix_list_12-3{list-style-type:none}#doc8312611 ul.lst-kix_list_12-2{list-style-type:none}#doc8312611 ul.lst-kix_list_12-1{list-style-type:none}#doc8312611 .lst-kix_list_17-8>li:before{content:»\0025aa «}#doc8312611 ul.lst-kix_list_12-0{list-style-type:none}#doc8312611 .
lst-kix_list_17-3>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_27-7>li{counter-increment:lst-ctn-kix_list_27-7}#doc8312611 .lst-kix_list_17-4>li:before{content:»o «}#doc8312611 ul.lst-kix_list_12-8{list-style-type:none}#doc8312611 ol.lst-kix_list_20-6.start{counter-reset:lst-ctn-kix_list_20-6 0}#doc8312611 ul.lst-kix_list_12-7{list-style-type:none}#doc8312611 .lst-kix_list_7-0>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-7.start{counter-reset:lst-ctn-kix_list_27-7 0}#doc8312611 .lst-kix_list_22-5>li:before{content:»\0025aa «}#doc8312611 ul.lst-kix_list_26-0{list-style-type:none}#doc8312611 .lst-kix_list_2-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_2-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_26-1{list-style-type:none}#doc8312611 ul.lst-kix_list_26-2{list-style-type:none}#doc8312611 ul.lst-kix_list_26-3{list-style-type:none}#doc8312611 .lst-kix_list_22-1>li:before{content:»o «}#doc8312611 .lst-kix_list_27-4>li:before{content:»» counter(lst-ctn-kix_list_27-4,lower-latin) «.
«}#doc8312611 .lst-kix_list_20-2>li{counter-increment:lst-ctn-kix_list_20-2}#doc8312611 .lst-kix_list_7-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_7-5{list-style-type:none}#doc8312611 .lst-kix_list_10-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_7-6{list-style-type:none}#doc8312611 ul.lst-kix_list_7-3{list-style-type:none}#doc8312611 ul.lst-kix_list_7-4{list-style-type:none}#doc8312611 .lst-kix_list_13-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_18-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_18-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_7-7{list-style-type:none}#doc8312611 ul.lst-kix_list_7-8{list-style-type:none}#doc8312611 ul.lst-kix_list_26-4{list-style-type:none}#doc8312611 ul.lst-kix_list_26-5{list-style-type:none}#doc8312611 ul.lst-kix_list_26-6{list-style-type:none}#doc8312611 ul.lst-kix_list_26-7{list-style-type:none}#doc8312611 ul.lst-kix_list_7-1{list-style-type:none}#doc8312611 ul.lst-kix_list_26-8{list-style-type:none}#doc8312611 ul.
lst-kix_list_7-2{list-style-type:none}#doc8312611 .lst-kix_list_27-0>li:before{content:»» counter(lst-ctn-kix_list_27-0,decimal) «. «}#doc8312611 ul.lst-kix_list_7-0{list-style-type:none}#doc8312611 .lst-kix_list_7-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_20-4>li{counter-increment:lst-ctn-kix_list_20-4}#doc8312611 .lst-kix_list_15-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_10-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_10-8>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_20-4.start{counter-reset:lst-ctn-kix_list_20-4 0}#doc8312611 .lst-kix_list_4-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-0>li{counter-increment:lst-ctn-kix_list_27-0}#doc8312611 ul.lst-kix_list_15-3{list-style-type:none}#doc8312611 ul.lst-kix_list_15-2{list-style-type:none}#doc8312611 .lst-kix_list_15-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_15-1{list-style-type:none}#doc8312611 .lst-kix_list_15-8>li:before{content:»\002022 «}#doc8312611 ul.
lst-kix_list_15-0{list-style-type:none}#doc8312611 .lst-kix_list_4-4>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_20-1.start{counter-reset:lst-ctn-kix_list_20-1 0}#doc8312611 .lst-kix_list_25-4>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_15-8{list-style-type:none}#doc8312611 ul.lst-kix_list_15-7{list-style-type:none}#doc8312611 ul.lst-kix_list_15-6{list-style-type:none}#doc8312611 .lst-kix_list_9-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_15-5{list-style-type:none}#doc8312611 ul.lst-kix_list_15-4{list-style-type:none}#doc8312611 .lst-kix_list_25-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_25-0{list-style-type:none}#doc8312611 ul.lst-kix_list_25-1{list-style-type:none}#doc8312611 ul.lst-kix_list_25-2{list-style-type:none}#doc8312611 .lst-kix_list_9-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_25-3{list-style-type:none}#doc8312611 ul.lst-kix_list_25-4{list-style-type:none}#doc8312611 .lst-kix_list_11-4>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_12-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-5>li{counter-increment:lst-ctn-kix_list_27-5}#doc8312611 ul.lst-kix_list_6-6{list-style-type:none}#doc8312611 ul.lst-kix_list_6-7{list-style-type:none}#doc8312611 ul.lst-kix_list_6-4{list-style-type:none}#doc8312611 .lst-kix_list_20-5>li:before{content:»» counter(lst-ctn-kix_list_20-5,lower-roman) «. «}#doc8312611 ul.lst-kix_list_6-5{list-style-type:none}#doc8312611 ul.lst-kix_list_6-8{list-style-type:none}#doc8312611 .lst-kix_list_28-8>li:before{content:»» counter(lst-ctn-kix_list_28-8,lower-roman) «. «}#doc8312611 ul.lst-kix_list_25-5{list-style-type:none}#doc8312611 .lst-kix_list_1-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_25-6{list-style-type:none}#doc8312611 .lst-kix_list_20-1>li:before{content:»» counter(lst-ctn-kix_list_20-1,lower-latin) «. «}#doc8312611 ul.lst-kix_list_25-7{list-style-type:none}#doc8312611 ul.lst-kix_list_25-8{list-style-type:none}#doc8312611 ul.lst-kix_list_6-2{list-style-type:none}#doc8312611 .
lst-kix_list_11-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_6-3{list-style-type:none}#doc8312611 ul.lst-kix_list_6-0{list-style-type:none}#doc8312611 .lst-kix_list_12-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_6-1{list-style-type:none}#doc8312611 .lst-kix_list_28-4>li:before{content:»» counter(lst-ctn-kix_list_28-4,lower-latin) «. «}#doc8312611 .lst-kix_list_1-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_13-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_28-3>li{counter-increment:lst-ctn-kix_list_28-3}#doc8312611 ul.lst-kix_list_14-4{list-style-type:none}#doc8312611 ul.lst-kix_list_14-3{list-style-type:none}#doc8312611 ul.lst-kix_list_14-2{list-style-type:none}#doc8312611 .lst-kix_list_13-4>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_14-1{list-style-type:none}#doc8312611 ul.lst-kix_list_14-0{list-style-type:none}#doc8312611 ul.lst-kix_list_14-8{list-style-type:none}#doc8312611 ul.lst-kix_list_14-7{list-style-type:none}#doc8312611 .
lst-kix_list_2-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_14-6{list-style-type:none}#doc8312611 ul.lst-kix_list_14-5{list-style-type:none}#doc8312611 .lst-kix_list_28-0>li:before{content:»» counter(lst-ctn-kix_list_28-0,decimal) «. «}#doc8312611 .lst-kix_list_1-8>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-8>li:before{content:»» counter(lst-ctn-kix_list_27-8,lower-roman) «. «}#doc8312611 .lst-kix_list_12-8>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_20-3.start{counter-reset:lst-ctn-kix_list_20-3 0}#doc8312611 .lst-kix_list_19-0>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_19-1>li:before{content:»o «}#doc8312611 ul.lst-kix_list_1-0{list-style-type:none}#doc8312611 .lst-kix_list_27-8>li{counter-increment:lst-ctn-kix_list_27-8}#doc8312611 .lst-kix_list_19-4>li:before{content:»o «}#doc8312611 .lst-kix_list_19-2>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_19-3>li:before{content:»\0025cf «}#doc8312611 ul.lst-kix_list_1-3{list-style-type:none}#doc8312611 ul.
lst-kix_list_1-4{list-style-type:none}#doc8312611 ul.lst-kix_list_1-1{list-style-type:none}#doc8312611 ul.lst-kix_list_1-2{list-style-type:none}#doc8312611 ul.lst-kix_list_1-7{list-style-type:none}#doc8312611 ul.lst-kix_list_1-8{list-style-type:none}#doc8312611 ul.lst-kix_list_1-5{list-style-type:none}#doc8312611 ul.lst-kix_list_1-6{list-style-type:none}#doc8312611 ol.lst-kix_list_27-5.start{counter-reset:lst-ctn-kix_list_27-5 0}#doc8312611 .lst-kix_list_19-8>li:before{content:»\0025aa «}#doc8312611 ol.lst-kix_list_20-8.start{counter-reset:lst-ctn-kix_list_20-8 0}#doc8312611 .lst-kix_list_19-5>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_19-6>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_19-7>li:before{content:»o «}#doc8312611 .lst-kix_list_28-5>li{counter-increment:lst-ctn-kix_list_28-5}#doc8312611 .lst-kix_list_20-5>li{counter-increment:lst-ctn-kix_list_20-5}#doc8312611 .lst-kix_list_18-0>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_18-1>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_18-2>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-0.start{counter-reset:lst-ctn-kix_list_27-0 0}#doc8312611 .lst-kix_list_27-4>li{counter-increment:lst-ctn-kix_list_27-4}#doc8312611 .lst-kix_list_27-1>li{counter-increment:lst-ctn-kix_list_27-1}#doc8312611 ul.lst-kix_list_22-0{list-style-type:none}#doc8312611 .lst-kix_list_2-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-1>li:before{content:»» counter(lst-ctn-kix_list_27-1,lower-latin) «. «}#doc8312611 ul.lst-kix_list_22-1{list-style-type:none}#doc8312611 ul.lst-kix_list_22-2{list-style-type:none}#doc8312611 ul.lst-kix_list_22-3{list-style-type:none}#doc8312611 ul.lst-kix_list_22-4{list-style-type:none}#doc8312611 .lst-kix_list_2-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-3>li:before{content:»» counter(lst-ctn-kix_list_27-3,decimal) «. «}#doc8312611 ul.lst-kix_list_22-5{list-style-type:none}#doc8312611 ul.lst-kix_list_22-6{list-style-type:none}#doc8312611 ul.lst-kix_list_22-7{list-style-type:none}#doc8312611 .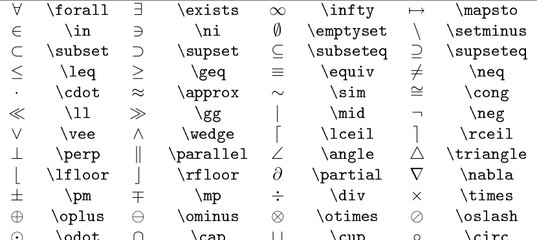
lst-kix_list_27-5>li:before{content:»» counter(lst-ctn-kix_list_27-5,lower-roman) «. «}#doc8312611 .lst-kix_list_18-6>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_3-7{list-style-type:none}#doc8312611 ul.lst-kix_list_3-8{list-style-type:none}#doc8312611 .lst-kix_list_10-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_18-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_18-8>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-3.start{counter-reset:lst-ctn-kix_list_27-3 0}#doc8312611 ul.lst-kix_list_3-1{list-style-type:none}#doc8312611 ul.lst-kix_list_22-8{list-style-type:none}#doc8312611 ul.lst-kix_list_3-2{list-style-type:none}#doc8312611 ul.lst-kix_list_3-0{list-style-type:none}#doc8312611 ul.lst-kix_list_3-5{list-style-type:none}#doc8312611 ul.lst-kix_list_3-6{list-style-type:none}#doc8312611 ul.lst-kix_list_3-3{list-style-type:none}#doc8312611 ul.lst-kix_list_3-4{list-style-type:none}#doc8312611 .lst-kix_list_10-7>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_20-1>li{counter-increment:lst-ctn-kix_list_20-1}#doc8312611 .lst-kix_list_10-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_10-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_11-7{list-style-type:none}#doc8312611 ul.lst-kix_list_11-6{list-style-type:none}#doc8312611 ol.lst-kix_list_20-8{list-style-type:none}#doc8312611 ul.lst-kix_list_11-5{list-style-type:none}#doc8312611 ul.lst-kix_list_11-4{list-style-type:none}#doc8312611 ul.lst-kix_list_11-3{list-style-type:none}#doc8312611 ol.lst-kix_list_20-5{list-style-type:none}#doc8312611 ul.lst-kix_list_11-2{list-style-type:none}#doc8312611 ol.lst-kix_list_20-4{list-style-type:none}#doc8312611 ul.lst-kix_list_11-1{list-style-type:none}#doc8312611 ol.lst-kix_list_20-7{list-style-type:none}#doc8312611 ul.lst-kix_list_11-0{list-style-type:none}#doc8312611 ol.lst-kix_list_20-6{list-style-type:none}#doc8312611 .lst-kix_list_9-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_28-1>li{counter-increment:lst-ctn-kix_list_28-1}#doc8312611 ol.
lst-kix_list_20-1{list-style-type:none}#doc8312611 ol.lst-kix_list_20-0{list-style-type:none}#doc8312611 ol.lst-kix_list_20-3{list-style-type:none}#doc8312611 ol.lst-kix_list_20-2{list-style-type:none}#doc8312611 ol.lst-kix_list_28-7.start{counter-reset:lst-ctn-kix_list_28-7 0}#doc8312611 ul.lst-kix_list_11-8{list-style-type:none}#doc8312611 .lst-kix_list_20-8>li:before{content:»» counter(lst-ctn-kix_list_20-8,lower-roman) «. «}#doc8312611 .lst-kix_list_9-0>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_21-1{list-style-type:none}#doc8312611 ul.lst-kix_list_21-2{list-style-type:none}#doc8312611 ul.lst-kix_list_21-3{list-style-type:none}#doc8312611 ul.lst-kix_list_21-4{list-style-type:none}#doc8312611 .lst-kix_list_20-0>li:before{content:»» counter(lst-ctn-kix_list_20-0,decimal) «. «}#doc8312611 ul.lst-kix_list_21-5{list-style-type:none}#doc8312611 ul.lst-kix_list_21-6{list-style-type:none}#doc8312611 ul.lst-kix_list_21-7{list-style-type:none}#doc8312611 ul.lst-kix_list_21-8{list-style-type:none}#doc8312611 .
lst-kix_list_9-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_9-4>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_11-3>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_21-0{list-style-type:none}#doc8312611 .lst-kix_list_20-6>li:before{content:»» counter(lst-ctn-kix_list_20-6,decimal) «. «}#doc8312611 ul.lst-kix_list_2-8{list-style-type:none}#doc8312611 .lst-kix_list_20-4>li:before{content:»» counter(lst-ctn-kix_list_20-4,lower-latin) «. «}#doc8312611 .lst-kix_list_11-5>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_2-2{list-style-type:none}#doc8312611 .lst-kix_list_20-2>li:before{content:»» counter(lst-ctn-kix_list_20-2,lower-roman) «. «}#doc8312611 ul.lst-kix_list_2-3{list-style-type:none}#doc8312611 ul.lst-kix_list_2-0{list-style-type:none}#doc8312611 ul.lst-kix_list_2-1{list-style-type:none}#doc8312611 .lst-kix_list_9-8>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_2-6{list-style-type:none}#doc8312611 .lst-kix_list_20-6>li{counter-increment:lst-ctn-kix_list_20-6}#doc8312611 .
lst-kix_list_1-1>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_2-7{list-style-type:none}#doc8312611 .lst-kix_list_11-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_2-4{list-style-type:none}#doc8312611 ul.lst-kix_list_2-5{list-style-type:none}#doc8312611 ul.lst-kix_list_10-0{list-style-type:none}#doc8312611 .lst-kix_list_1-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_28-6>li{counter-increment:lst-ctn-kix_list_28-6}#doc8312611 .lst-kix_list_28-3>li:before{content:»» counter(lst-ctn-kix_list_28-3,decimal) «. «}#doc8312611 .lst-kix_list_28-7>li:before{content:»» counter(lst-ctn-kix_list_28-7,lower-latin) «. «}#doc8312611 ul.lst-kix_list_10-8{list-style-type:none}#doc8312611 ul.lst-kix_list_10-7{list-style-type:none}#doc8312611 .lst-kix_list_1-7>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_10-6{list-style-type:none}#doc8312611 ul.lst-kix_list_10-5{list-style-type:none}#doc8312611 ul.lst-kix_list_10-4{list-style-type:none}#doc8312611 ul.lst-kix_list_10-3{list-style-type:none}#doc8312611 .
lst-kix_list_1-5>li:before{content:»\002022 «}#doc8312611 ul.lst-kix_list_10-2{list-style-type:none}#doc8312611 .lst-kix_list_28-5>li:before{content:»» counter(lst-ctn-kix_list_28-5,lower-roman) «. «}#doc8312611 ul.lst-kix_list_10-1{list-style-type:none}#doc8312611 .lst-kix_list_2-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-7>li:before{content:»» counter(lst-ctn-kix_list_27-7,lower-latin) «. «}#doc8312611 .lst-kix_list_2-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_28-1>li:before{content:»» counter(lst-ctn-kix_list_28-1,lower-latin) «. «}#doc8312611 .lst-kix_list_20-8>li{counter-increment:lst-ctn-kix_list_20-8}#doc8312611 .lst-kix_list_3-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_3-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_26-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_26-7>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_8-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_8-2>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_3-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_21-2>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_8-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_8-6>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_28-0.start{counter-reset:lst-ctn-kix_list_28-0 0}#doc8312611 .lst-kix_list_26-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_26-3>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_3-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_21-6>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_21-7>li:before{content:»o «}#doc8312611 .lst-kix_list_11-2>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-2.start{counter-reset:lst-ctn-kix_list_27-2 0}#doc8312611 .lst-kix_list_21-3>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_16-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_25-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_17-1>li:before{content:»o «}#doc8312611 .lst-kix_list_25-3>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_16-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_16-2>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_27-1.start{counter-reset:lst-ctn-kix_list_27-1 0}#doc8312611 .lst-kix_list_16-5>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_28-6.start{counter-reset:lst-ctn-kix_list_28-6 0}#doc8312611 ol.lst-kix_list_28-5.start{counter-reset:lst-ctn-kix_list_28-5 0}#doc8312611 .lst-kix_list_17-2>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_17-6>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_17-5>li:before{content:»\0025aa «}#doc8312611 .lst-kix_list_2-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-2>li:before{content:»» counter(lst-ctn-kix_list_27-2,lower-roman) «. «}#doc8312611 .lst-kix_list_22-3>li:before{content:»\0025cf «}#doc8312611 .lst-kix_list_7-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_7-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-6>li:before{content:»» counter(lst-ctn-kix_list_27-6,decimal) «.
«}#doc8312611 .lst-kix_list_28-2>li{counter-increment:lst-ctn-kix_list_28-2}#doc8312611 ol.lst-kix_list_28-4.start{counter-reset:lst-ctn-kix_list_28-4 0}#doc8312611 .lst-kix_list_22-7>li:before{content:»o «}#doc8312611 .lst-kix_list_18-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_13-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_20-3>li{counter-increment:lst-ctn-kix_list_20-3}#doc8312611 ol.lst-kix_list_28-1.start{counter-reset:lst-ctn-kix_list_28-1 0}#doc8312611 .lst-kix_list_15-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_10-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_28-4>li{counter-increment:lst-ctn-kix_list_28-4}#doc8312611 .lst-kix_list_20-7>li:before{content:»» counter(lst-ctn-kix_list_20-7,lower-latin) «. «}#doc8312611 .lst-kix_list_4-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_4-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_15-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_25-6>li:before{content:»\002022 «}#doc8312611 .
lst-kix_list_10-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_9-1>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_9-5>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_12-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_11-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_20-3>li:before{content:»» counter(lst-ctn-kix_list_20-3,decimal) «. «}#doc8312611 .lst-kix_list_1-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_27-6>li{counter-increment:lst-ctn-kix_list_27-6}#doc8312611 .lst-kix_list_28-6>li:before{content:»» counter(lst-ctn-kix_list_28-6,decimal) «. «}#doc8312611 .lst-kix_list_1-6>li:before{content:»\002022 «}#doc8312611 ol.lst-kix_list_28-2.start{counter-reset:lst-ctn-kix_list_28-2 0}#doc8312611 .lst-kix_list_12-6>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_2-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_13-2>li:before{content:»\002022 «}#doc8312611 .lst-kix_list_28-2>li:before{content:»» counter(lst-ctn-kix_list_28-2,lower-roman) «.
«}#doc8312611 ol{margin:0;padding:0}#doc8312611 .c13{border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-right-width:1pt;border-left-color:#000000;vertical-align:top;border-right-color:#000000;border-left-width:1pt;border-top-style:solid;border-left-style:solid;border-bottom-width:1pt;width:219.2pt;border-top-color:#000000;border-bottom-style:solid}#doc8312611 .c20{border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-right-width:1pt;border-left-color:#000000;vertical-align:top;border-right-color:#000000;border-left-width:1pt;border-top-style:solid;border-left-style:solid;border-bottom-width:1pt;width:223.3pt;border-top-color:#000000;border-bottom-style:solid}#doc8312611 .c1{padding-top:0pt;padding-bottom:0pt;line-height:1.5;orphans:2;widows:2;text-align:justify;direction:ltr}#doc8312611 .c2{padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;direction:ltr;height:11pt}#doc8312611 .
c10{padding-top:0pt;padding-bottom:0pt;line-height:1.5;orphans:2;widows:2;direction:ltr}#doc8312611 .c5{padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;direction:ltr}#doc8312611 .c12{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc8312611 .c26{vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-weight:bold}#doc8312611 .c0{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc8312611 .c27{vertical-align:baseline;font-size:11.5pt;font-family:»Times New Roman»;font-weight:normal}#doc8312611 .c11{vertical-align:baseline;font-size:11.5pt;font-family:»Times New Roman»;font-weight:bold}#doc8312611 .c23{background-color:#ffffff;max-width:467.7pt;padding:63.8pt 42.5pt 42.5pt 85pt}#doc8312611 .c24{margin-left:30.6pt;border-collapse:collapse;margin-right:auto}#doc8312611 .c19{padding:0;margin:0}#doc8312611 .c15{text-decoration:underline;font-style:italic}#doc8312611 .c4{text-decoration:underline;font-style:normal}#doc8312611 .
c18{text-decoration:none;font-style:normal}#doc8312611 .c8{padding-left:0pt}#doc8312611 .c16{color:#3a3a3a}#doc8312611 .c17{height:0pt}#doc8312611 .c22{text-decoration:underline}#doc8312611 .c25{text-align:justify}#doc8312611 .c6{color:#000000}#doc8312611 .c21{color:#ff0000}#doc8312611 .c14{text-align:right}#doc8312611 .c3{height:11pt}#doc8312611 .c7{margin-left:36pt}#doc8312611 .c9{text-align:center}#doc8312611 .title{padding-top:24pt;color:#000000;font-weight:bold;font-size:36pt;padding-bottom:6pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 .subtitle{padding-top:18pt;color:#666666;font-size:24pt;padding-bottom:4pt;font-family:»Georgia»;line-height:1.15;page-break-after:avoid;font-style:italic;orphans:2;widows:2;text-align:left}#doc8312611 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc8312611 p{margin:0;color:#000000;font-size:11pt;font-family:»Arial»}#doc8312611 h2{padding-top:24pt;color:#000000;font-weight:bold;font-size:24pt;padding-bottom:6pt;font-family:»Arial»;line-height:1. 15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 h3{padding-top:18pt;color:#000000;font-weight:bold;font-size:18pt;padding-bottom:4pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 h4{padding-top:14pt;color:#000000;font-weight:bold;font-size:14pt;padding-bottom:4pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 h5{padding-top:12pt;color:#000000;font-weight:bold;font-size:12pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 h5{padding-top:11pt;color:#000000;font-weight:bold;font-size:11pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 h6{padding-top:10pt;color:#000000;font-weight:bold;font-size:10pt;padding-bottom:2pt;font-family:»Arial»;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8312611 ]]>Откуда взялись математические символы
Содержание
Введение…………………………………………………………………………………….
.2
1История возникновения математических символов ……………………………………3
1.1Равенство…………………………………………………………………………3
1.2.Сложение …………….………………………………………………………….3
1.3Вычитание………………………………………………………………………..4
1.4Умножение……………………………………………………………………….4
1.5Деление……………………………………………………………………………4
1.6. Примерно равно…………………………………………………………………4
2. Практическая часть………………………………………………………………………5
3. Заключение……………………………………………………………………………….6
Библиография……………………………………………………………………………….7
Введение.
История математики тысячами нитей связана с историей других наук, историей техники, историей искусства, она — существенная часть человеческой культуры. В ней ясно обозначен вклад в математику учёных всего мира. Любая наука могла бы гордиться такой историей, как история математики. Преемственность не нарушали ни многовековые перерывы в развитии математической мысли, ни революции, ни войны.
Человечество говорит более чем на 2000 языках. Каждая народность имеет свой язык, свою культуру. Но есть язык, который понятен каждому грамотному человеку – это язык математики. Символика математического языка во всем мире одна и та же. Любая формула, любое математическое выражение, записанное при помощи цифр и знаков действий, имеет один и тот же смысл для всех народов мира. К этому международному языку математики люди пришли не сразу. Путь был длинный и сложный. Считать люди стали давно, еще тогда, когда о письменности не было никакого понятия. В общем, самым впечатляющим в этой истории является то, что символы, которые впервые появились в печати лишь около пятисот лет назад, стали частью того, что является, видимо, наиболее универсальным «языком». Живёте вы в Америке или в Сибири, все равно вы точно знаете, что означают эти символы.
Целью работы является:
- Познакомиться с историей возникновения математических знаков из разных источников.
- Применить старинные математические знаки к написанию современных примеров по математике
Мной были поставлены следующие задачи:
- Изучить литературу по теме исследования;
- Рассмотреть историю возникновения математических знаков и символов;
- Составить математические примеры, используя старинные математические обозначения
Для решения поставленных задач были использованы следующие методы:
изучение, анализ, обобщение.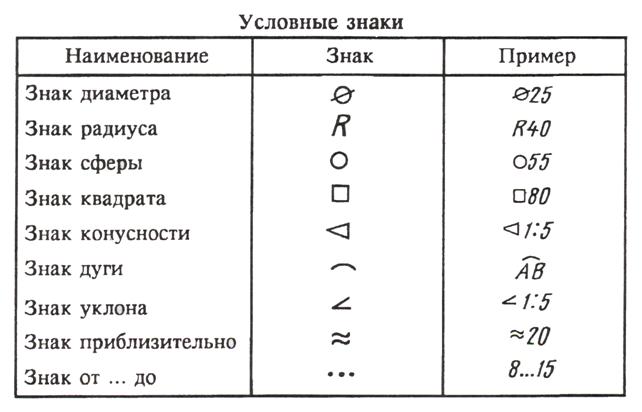
История возникновения математических символов.
Равенство.
Знак равенства предложил уэльский врач и математик Роберт Рекорд в 1557 году; начертание символа было намного длиннее нынешнего, так как имитировало изображение двух параллельных отрезков. Автор пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. Символ Рекорда получил распространение далеко не сразу. Распространению символа Рекорда мешало то обстоятельство, что с античных времён такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным. В континентальной Европе знак «=» был введён Готфридом Лейбницем только на рубеже XVII–XVIII веков, то есть более чем через 100 лет, после смерти впервые использовавшего его для этого Роберта Рекорда.
Сложение и вычитание.
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда.
В самом деле, кто-то должен был изобрести эти символы. Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Когда я начал изучать историю этих знаков, я обнаружил, к своему удивлению, что они появились вовсе не в глубокой древности. Многое из того, что нам известно, происходит из всеобъемлющего и впечатляющего исследования 1928-1929 гг., которое до сих пор остается непревзойденным. Это “История математических обозначений’’ швейцарско-американского историка математики Флориана Каджори (1859-1930).
Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’. В знаменитом египетском папирусе Ахмеса — пара ног, идущих вперед, обозначает сложение, а уходящих — вычитание. В конце пятнадцатого века французский математик Шике и итальянский Пачоли использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.
Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ.
Видман сам ввёл его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест “†’’, иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид “’’.
Вычитание.
Знак минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Он используется в учебнике Яна Видмана «Быстрый и приятный счёт для всех торговцев», изданном в 1489 году. До этого вычитание обозначалось буквой m (от латинского minus «менее, меньше»). Происхождение этого символа неясно, но, скорее всего, он ранее использовался в торговом деле как признак убытка. Этот символ вскоре получил общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
Обозначения вычитания были несколько менее причудливыми, но, возможно, более запутанными (для нас, по крайней мере), так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
Деление.
Уильям Оутред в качестве знака деления использовал косую черту /. Двоеточием деление стал обозначать Готфрид Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также горизонтальная черта дроби, употреблявшаяся ещё у Герона, Диофанта и в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложил Иоганн Ран в 1659 году.
Умножение.
Знак умножения в виде косого крестика ввёл в 1631 году англичанин Уильям Оутред. До него использовали чаще всего букву M, хотя предлагались и другие обозначения: символ прямоугольника, звёздочка.
Позднее Готфрид Вильгельм Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у немецкого астронома и математика Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560 –1621).
Примерно равно, приблизительно равно.
Знак «≈» (примерно равно) ввёл в использование как символ отношения «примерно равно» немецкий математик и физик Адам Вильгельм Зигмунд Гюнтер в 1882 году.
Больше, меньше.
Эти два знака ввёл в использование английский астроном, математик, этнограф и переводчик Томас Гарриот в 1631 году, до этого использовали слова «больше» и «меньше».
Практическая часть.
Познакомившись с историей возникновения математических символов, я записал простые примеры из курса математики 5 класса, применяя старинные математические знаки.
Старинная запись | Современная запись |
| |
| |
Данные примеры вызвали большой интерес у моих одноклассников.
Конечно, без знаний полученных мной в ходе работы и я не смог бы справится с такими примерами. Поэтому считаю, что проделанная мной работа полезна для развития познавательности и расширения кругозора.
Заключение.
Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю. М.В.Ломоносов говорил: «Математика ум в порядок приводит». Одним словом, математика учит нас учиться приобретать знания. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Поэтому считаю, что проделанная мной работа полезна для развития познавательности и расширения кругозора.
Список используемой литературы .
1.Что? Зачем? Почему? Большая книга вопросов и ответов. Пер.Мишиной К., А Зыковой -М: Издательство ЭКСМО, 2007
2.
Глейзер Г.И. История математики в школе VII-VIII кл. Пособие для учителей. М: Просвещение, 1982
3. Рыбников К.А. История математики. Издательство Московского Университета, 1974
4. Интернет. www математические символы.
Как ввести знак параграфа и математические символы
Количество кнопок на клавиатуре ограничено и далеко не все символы и значки, которые вы захотите использовать в своих целях, доступны очевидным образом. В ОС Windows имеется таблица символов, из которой можно копировать любой значок, однако пользоваться ей каждый раз не так-то удобно.
Каждый символ имеет свое числовое обозначение в так называемой таблице ASCII, благодаря которой компьютер понимает, что именно вы вводите с клавиатуры. Это касается латинских и кириллических букв, а также любых других значков.
При этом, даже если какого-то символа нет на самой клавиатуре, то ввести его можно, если знать точный код из таблицы ASCII.
Узнать код можно в стандартном приложении Windows «Таблица символов». Просто выделив тот или иной значок в правом нижнем углу программы появится подсказка, как именно ввести символ прямо с клавиатуры. Для этого используется зажатой клавиша Alt и последовательный набор цифр на цифровой клавиатуре (ее может не быть на некоторых ноутбуках, а ввод цифр с раскладки, непосредственно над буквами, работать таким образом не будет). При это должна быть активной клавиша Num Lock, иначе вместо цифр будут использоваться клавиши перемещения.
Важный момент: клавиша Alt отпускается только после того, как введены все цифры. Сами цифры нажимаются не одновременно, как это бывает при использовании «горячих клавиш», а по очереди. Скажем, для ввода знака «параграф» необходимо зажать Alt, затем на бухгалтерской клавиатуре нажать 0, потом 1, потом 6, потом 7 и опустить Alt.
§ – Alt+0167 (а также Alt+21) знак параграфа
º – Alt+0186 обозначение градусов Цельсия
£ – Alt+0163 знак фунта
€ – Alt+0128 знак евро
† – Alt+0134 символ креста
± – Alt+0177 символ плюс/минус
≤ – Alt+8804 знак меньше или равно
≥ – Alt+8805 знак больше или равно
≈ Alt+8776 знак примерно равно
≠ – Alt+8800 знак не равно
Самих цифр, нажимаемых совместно с клавишей Alt, не обязательно должно быть четыре. Для многих символов используются по две-три цифры. Например, для обозначения мужского символа ♂ используется сочетание Alt+11, я для ввода женского символа ♀ – Alt+12. Попробуйте самостоятельно различные сочетания и посмотрите, что получится. Более подробно информацию о вводе специальных значков и символов можно посмотреть на Википедии.
★ Знак равенства — математические знаки .. Информация
Пользователи также искали:
знак больше или равно,
знак равенства аватария,
знак равенства это,
знак равенства фестиваль,
знак равенства инстаграм,
знак равенства кулак,
знак равенства людей,
знак равенства в математике,
Знак,
знак,
равенства,
Знак равенства,
знак равенства людей,
знак равенства это,
знак больше или равно,
знак равенства инстаграм,
знак равенства в математике,
знак равенства аватария,
математике,
инстаграм,
знак равенства кулак,
фестиваль,
кулак,
людей,
больше,
равно,
аватария,
знак равенства фестиваль,
знак равенства,
математические знаки.
знак равенства,
В каком веке появился знак больше. История математических обозначений
Балагин Виктор
С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.
Скачать:
Предварительный просмотр:
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
Работу выполнил
Ученик 7-а класса
ГБОУ СОШ № 574
Балагин Виктор
2012-2013 уч.год
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
- Введение
Слово математика пришло к нам из древнегреческого, где μάθημα означало «учиться», «приобретать знания».
И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю. М.В.Ломоносов говорил: «Математика ум в порядок приводит». Одним словом, математика учит нас учиться приобретать знания.
Математика – это первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число 35 в виде нарисованных в ряд 35 палочек. Можно сказать, что 1 палочка – это первый математический символ.
Математическая «письменность», которую мы сейчас используем — от обозначений неизвестных буквами x, y, z до знака интеграла — складывалась постепенно. Развитие символики упрощало работу с математическими операциями и способствовало развитию самой математики.
С древнегреческого «символ» (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию.
С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.
2. Знаки сложения, вычитания
История математических обозначений начинается с палеолита. Этим временем датируются камни и кости с насечками, использовавшимися для счета. Наиболее известный пример —
кость Ишанго
.
Знаменитая кость из Ишанго (Конго) датируемая примерно 20 тысяч лет до новой эры, доказывает, что уже в то время человек выполнял достаточно сложные математические операции. Насечки на кости использовались для сложения и наносились группами, символизируя сложения чисел.
В Древнем Египте была уже намного более продвинутая система обозначений. Например, в папирусе Ахмеса в качестве символа сложения используется изображение двух ног, идущих вперед по тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полуэллиптическую кривую для вычитания.
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. Происхождение этих символов неясно. Одна из версий — они ранее использовались в торговом деле как признаки прибыли и убытка.
Считается, так же, что наш знак
происходит от одной из форм слова “et’’, которое по-латыни значит “и’’.
Выражение
a + b
писалось на латыни так:
a et b
. Постепенно, из-за частого использования, от знака »
et
» осталось только »
t
» , которое, со временем превратилось в »
+
«. Первым человеком, который, возможно, использовал знак
как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “ ’’ или “ ’’ (обозначая “плюс’’) для сложения и “ ’’ или “ ’’ (обозначая “минус’’) для вычитания.
Обозначения вычитания были более запутанными, так как вместо простого знака “ ” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
Первое использование современного алгебраического знака “
” относится к немецкой рукописи по алгебре 1481 г.
, которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: «
» и « — » . Систематическое использование знаков «
» и « — » для сложения и вычитания встречается у
Иоганна Видмана
.
Немецкий математик Иоганн Видманн (1462-1498) первым использовал оба знака для пометок присутствия и отсутствия студентов на своих лекциях. Правда, есть сведения, что он «позаимствовал» эти знаки у малоизвестного профессора Лейпцигского университета. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака
и
, в труде «Быстрый и приятный счёт для всех торговцев» (ок. 1490)
Как исторический курьез, стоит отметить, что даже после принятия знака
не все использовали этот символ. Видман сам ввел его как греческий крест
(знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак.
Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест « † », иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид «
».
3.Знак равенства
Знак равенства в математике и других точных науках пишут между двумя идентичными по своему размеру выражениями. Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный). В
античной и средневековой математике
равенство обозначалось словесно, например, est egale, или использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые буквы слова “равный’’, но это не было общепринятым. Знак равенства «=» ввел в 1557 году уэльский врач и математик
Роберт Рекорд
(Recorde R., 1510-1558). Математическим символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя одинаковыми горизонтальными параллельными отрезками, гораздо более длинными, чем те, что используются сегодня.
Английский математик Роберт Рекорд был первым, кто начал использовать символ «равенство», аргументируя словами: «никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». Но ещё в
XVII веке
Рене Декарт
использовал аббревиатуру “ae’’.
Франсуа Виет
знаком равенства обозначал вычитание. Некоторое время распространению символа Рекорда мешало то обстоятельство, что такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным. Распространение знак получил только после работ Лейбница на рубеже XVII-XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого
Роберта Рекорда
. На его могильной плите нет слов – просто вырезан знак «равно».
Родственные символы для обозначения приблизительного равенства «≈» и тождества «≡» являются совсем молодыми — первый введен в 1885 году Гюнтером, второй — в 1857 году Риманом
4. Знаки умножения и деления
Знак умножения в виде крестика («х») ввел англиканский священник-математик
Уильям Отред
в
1631 году
.
До него для знака умножения использовали букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон
,
), звёздочка (Иоганн Ран
,
).
Позднее Лейбниц заменил крестик на точку (конец XVII века ), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век ) и английского учёного Томаса Хэрриота (1560-1621).
Для обозначения действия деления Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц . До них часто использовали также букву D. Начиная с Фибоначчи , используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. Деление в виде обелюс («÷») ввел швейцарский математик Иоганн Ран (ок. 1660)
5. Знак процента .
Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта (1685). В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento).
Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
6.Знак бесконечности
Нынешний символ бесконечности «∞» ввел в употребление Джон Уоллис в 1655 году. Джон Уоллис издал большой трактат «Арифметика бесконечного» (лат. Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque Difficiliora Matheseos Problemata ), где ввёл придуманный им символ бесконечности . До сих пор так и не известно, почему он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных гипотез связывает происхождение этого символа с латинской буквой «М», которую римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента) математиком Бернулли приблизительно сорок лет спустя.
Другая версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия «бесконечность»: движение
без конца
. По линиям числа 8 можно совершать, как по велотреку, бесконечное движение.
Для того, чтобы не путать введенный знак с числом 8, математики решили располагать его горизонтально. Получилось
. Такое обозначение cтало стандартным для всей математики, не только алгебры. Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не поворачивай — она не изменится. Поэтому выбор и пал именно на 8.
Другой вариант — змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца.
Многие считают, что лист Мёбиуса является прародителем символа бесконечности , т.к символ бесконечности был запатентован после изобретения устройства «лента Мебиуса» (названный в честь математика девятнадцатого столетия Мебиуса). Лента Мебиуса — полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Однако по имеющимся историческим сведениям символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса
7.
Знаки
угл
а и
перпендикулярно
сти
Символы « угол » и « перпендикулярно » придумал в 1634 году французский математик Пьер Эригон . Символ перпендикулярности у него был перевёрнут, напоминая букву T. Символ угла напоминал значок , современную форму ему придал Уильям Отред ().
8. Знак параллельност и
Символ « параллельности » известен с античных времён, его использовали Герон и Папп Александрийский . Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально (Отред (1677), Керси (John Kersey ) и др. математики XVII века)
9. Число пи
Общепринятое обозначение числа, равного отношению длины окружности к ее диаметру (3,1415926535…), впервые образовал Уильям Джонс в 1706 году , взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр , то есть длина окружности. Это сокращение понравилось Эйлеру , труды которого закрепили обозначение окончательно.
10.
Синус и косинус
Интересно появление синуса и косинуса.
Sinus с латинского — пазуха, впадина. Но история у такого названия долгая. Далеко в тригонометрии продвинулись индийские математики в районе 5 века. Самого слова «тригонометрия» не было, оно было введено Георгом Клюгелем в 1770 году.) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для краткости называли просто — джия (тетива). Когда арабы переводили работы индусов с санскрита, они не стали переводить «тетиву» на арабский, а просто транскрибировали слово арабскими буквами. Получилась джиба. Но так как в слоговой арабской письменности краткие гласные не обозначаются, то реально остается дж-б, что похоже на другое арабское слово — джайб (впадина, пазуха). Когда Герард Кремонский в 12 веке переводил арабов на латынь, он перевел это слово как sinus, что по-латыни также означает пазуху, углубление.
Косинус появился автоматически, т.
к. индусы называли его коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука на санскрите.
Современные краткие обозначения
и
введены
Уильямом Отредом
и закреплены в трудах
Эйлера
.
Обозначения тангенса/котангенса имеют намного более позднее происхождение (английское слово tangent происходит от латинского tangere — касаться). И даже до сих пор нет унифицированного обозначения — в одних странах чаще используется обозначение tan, в других — tg
11. Сокращение «Что и требовалось доказать» (ч.т.д.)
«
Quod erat demonstrandum
» (квол эрат лэмонстранлум).
Греческая фраза имеет значение «что требовалось доказывать», а латинская — «что нужно было показать». Этой формулой заканчивается каждое математическое рассуждение великого греческого математика Древней Греции Эвклида (III в. до н. э.). В переводе с латинского — что и требовалось доказать. В средневековых научных трактатах эту формулу писали часто в сокращенном виде: QED.
12. Математические обозначения.
Символы | История символов |
Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии. | |
× ∙ | Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621). |
/ : ÷ | Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века. |
= | Знак равенства предложил Роберт Рекорд (1510-1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем. |
Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше. | |
% | Символ процента появляется в середине XVII века сразу в нескольких источниках, его происхождение неясно. Есть гипотеза, что он возник от ошибки наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. |
√ | Знак корня впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы слова radix (корень). Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня. |
a
n | Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676). |
() | Скобки появились у Тартальи (1556) для подкоренного выражения, но большинство математиков предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц. |
Знак суммы ввёл Эйлер в 1755 году | |
Знак произведения ввёл Гаусс в 1812 году | |
i | Букву i как код мнимой единицы:
предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый). |
π | Общепринятое обозначение числа 3.14159… образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр, то есть длина окружности. |
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). | |
y» | Краткое обозначение производной штрихом восходит к Лагранжу. |
Символ предела появился в 1787 году у Симона Люилье (1750-1840). | |
Символ бесконечности придумал Валлис, опубликован в 1655 году. |
Более вероятно, что это скорописный коммерческий значок, возникший лет на 100 раньше.
13.
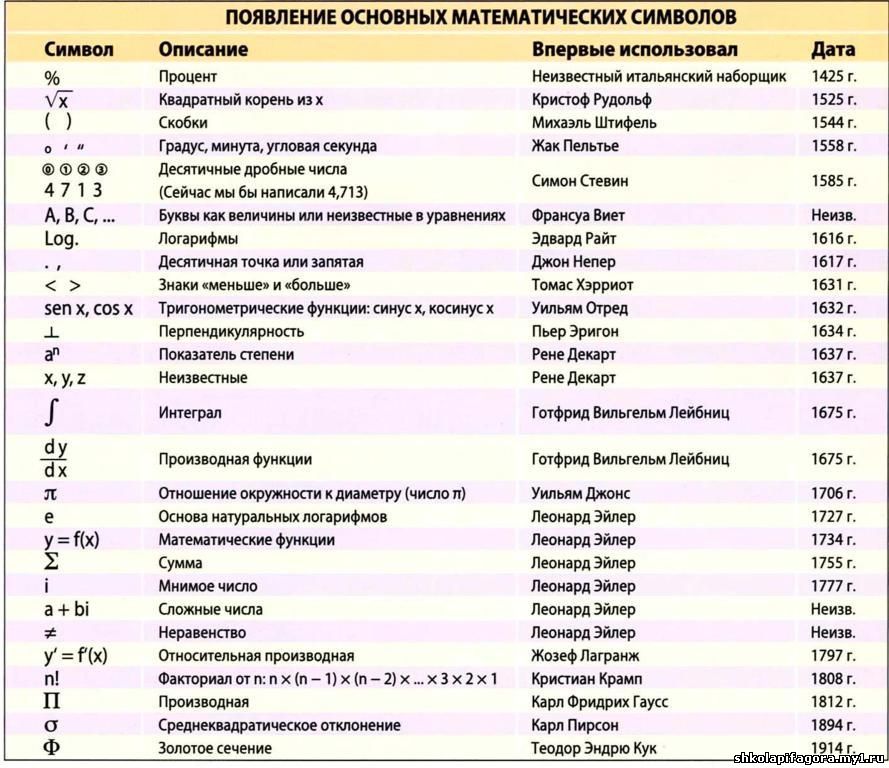Заключение
Математическая наука необходима для цивилизованного общества. Математика содержится во всех науках. Математический язык смешивается с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые создают новые технологии. Сохранившиеся открытия дают возможность решать сложные математически задачи. И древний математический язык нам понятен, а открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли физические законы. Мы изучаем их в школе. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение математики необходимо для новых открытий.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.
google.com
Подписи к слайдам:
Математические символы Работу выполнил ученик 7-а класса школы №574 Балагин Виктор
Символ (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию. Знаки – это математические условные обозначения, предназначенные для записи математических понятий, предложений и выкладок.
Кость Ишанго Часть папируса Ахмеса
+ − Знаки плюса и минуса. Сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). Выражение a + b писалось на латыни так: a et b .
Обозначения вычитания. ÷ ∙ ∙ или ∙ ∙ ∙ Рене Декарт Марен Мерсенн
Страница из книги Иоганна Видман н а. В 1489 году Иоганн Видман издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “ Коммерческая арифметика’’), в которой присутствовали оба знака + и —
Обозначения сложения.
Христиан Гюйгенс Дэвид Юм Пьер де Ферма Эдмунд (Эдмонд) Галлей
Знак равенства Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный).
Знак равенства Предложил в 1557 году английский математик Роберт Рекорд «Никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». В континентальной Европе знак равенства был введён Лейбницем
× ∙ Знак умножения Ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x . Уильям Отред Готфрид Вильгельм Лейбниц
Процент. Матье де ла Порт (1685). Сотая доля целого, принимаемого за единицу. «процент» — «pro centum», что означает — «на сто». «cto» (сокращённо от cento). Н аборщик принял «cto» за дробь и напечатал «%».
Бесконечность. Джон Уоллис Джон Уоллис в 1655 году ввёл придуманный им символ. Змей, пожирающий свой хвост, символизировал различные процессы, не имеющие начала и конца.
Символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса Лента Мебиуса – полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Август Фердинанд Мёбиус
Угол и перпендикуляр. Символы придумал в 1634 году французский математик Пьер Эригон. Символ угла у Эригона напоминал значок. Символ перпендикулярности был перевёрнут, напоминая букву T . Современную форму этим знакам придал Уильям Отред (1657).
Параллельность. Символ использовали Герон Александрийский и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально. Герон Александрийский
Число пи. π ≈ 3,1415926535… Уильям Джонс в 1706 году π εριφέρεια -окружность и π ερίμετρος — периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно. Уильям Джонс
sin Синус и косинус cos Sinus (с латинского) – пазуха, впадина.
коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука Современные краткие обозначения введены Уильямом Отредом и закреплены в трудах Эйлера. «арха-джива» — у индийцев -«полутетива» Леонард Эйлер Уильям Отред
Что и требовалось доказать (ч.т.д.) « Quod erat demonstrandum » QED. Этой формулой заканчивается каждое математическое рассуждение великого математика Древней Греции Эвклида (III в. до н. э.).
Древний математический язык нам понятен. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики.
И в черте города, и за городом нужно движение транспорта как-то регулировать. Не везде хорошая дорога и нет опасных поворотов или ещё каких потенциальных опасностей. Как о них сообщить водителю и пешеходу?
Можно повесить здоровущий информационный щит. А можно поставить не очень большой, но не менее информативный условный знак, который будет понятен всем, кто хоть немного знаком с правилами дорожного движения.
Согласно официальной формулировке, дорожный знак — это стандартизированный графический рисунок, устанавливаемый у дороги для сообщения определённой информации участникам дорожного движения. И устанавливают их в строго определённых местах, нередко — рядом со светофорами или недалеко от них.
История и эволюция
Конечно, дорожные знаки в современном смысле этого слова появились не так уж давно: 110 лет назад в самом начале 20 века — в 1903 году. Но не будем забегать вперёд, начнём с самого начала.
Давным-давно, когда в Южной Европе ещё ходили в тогах… В общем, дело было в Древней Греции и не менее древнем Риме. Именно в античные времена впервые задумались о введении дорожных знаков и вообще правил дорожного движения.
Сегодня на любой трассе через каждый километр стоять столбики с указанием того, какой это километр. В древности расстояния измеряли в других единицах, но сути это не меняет. В Греции, например, вдоль дорог через определённые промежутки ставили специальные столбы — гермы (они получили своё название от имени бога Гермеса, который помимо всего прочего считался покровителем путешественников).
Через некоторое время на этих столбах стали помещать скульптурные изображения политических деятелей и видных философов, а затем — и надписи.
Куда основательнее подошли к этому вопросу римляне. Возле одного из главных храмов города был установлен специальный мильный столб, от которого вели отсчёт все дороги империи. На самых значимых транспортных магистралях империи устанавливались особые столбы цилиндрической формы. На них размещались специальные информационные надписи, сообщающие о расстоянии от Римского форума.
Ещё дальше пошёл Юлий Цезарь. Вечный город к тому времени уже был самым настоящим мегаполисом (хоть и античным), по улицам перемещалось невероятное число людей, среди которых были и приезжие, и торговцы, и местные жители. Чтобы никто никого не задавил, потребовалось регламентировать хотя бы некоторые моменты:
- Появились улицы с односторонним движением.
- Проезд частных колесниц, повозок и экипажей по Риму был запрещен с восхода солнца до конца «рабочего дня», что приблизительно соответствовало двум часам до его захода.
- Иногородние были обязаны оставлять свой транспорт за чертой города и могли передвигаться по улицам только пешком или в наемных паланкинах.
За соблюдением этих правил следила специально созданная служба. В её ряды набирали, главным образом, вольноотпущенных, которые прежде выполняли функции пожарных.
Верстовые столбы устанавливали не только в Греции и Риме. При царе Фёдоре Ивановиче верстовые столбы начали ставить и на дорогах государства Российского. При Петре Первом установка придорожных столбов была закреплена законодательно. Предписывалось и размещать на них надписи с указанием направлений и расстояний до того или иного населённого пункта.
С развитием автомобилестроения возникла новая проблема: как предупредить дорожно-транспортные происшествия. Понятное дело, что и во времена конных экипажей случались аварии, но лошади, всё-таки, живые существа и могут среагировать не дожидаясь действий возницы. А вот один водитель, да ещё на незнакомой дороге.
.. В итоге на улицах Парижа были установлены три дорожных знака: «крутой спуск», «опасный поворот», «неровная дорога».
Чтобы определиться с тем, каким образом обезопасить дорожное движение в 1906 году европейские автолюбители собрались и разработали «Международную конвенцию относительно передвижения автомобилей».
Документ этот содержал требования к самому автомобилю и основные правила дорожного движения. Кроме этого вводились четыре дорожных знака: «неровная дорога», «извилистая дорога», «перекресток», «пересечение с железной дорогой».
Устанавливать знаки следовало за 250 метров до опасного участка. Немного позже, после ратификации конвенции, дорожные знаки появились и в России. Причём первые российские автолюбители не утруждали себя внимательным отношением к этим знакам.
Разновидности дорожных знаков
Последним из документов, в котором прописаны все тонкости, связанные с дорожными знаками, является Венская конвенция, принятая 8 ноября 1968. Конвенция была разработана во время конференции ЮНЕСКО с 7 октября по 8 ноября 1968 в Вене и вступила в силу 6 июня 1978 года.
Согласно этой конвенции, выделяется восемь групп дорожных знаков:
- Предупреждающие знаки.
- Знаки преимущественного права проезда.
- Запрещающие и ограничивающие знаки.
- Предписывающие знаки.
- Знаки особых предписаний.
- Информационные знаки, знаки, обозначающие объекты и знаки сервиса.
- Указатели направлений и информационно-указательные знаки.
- Дополнительные таблички.
Знаки в разных странах
Несмотря на существование международного стандарта, в разных странах мира дорожные знаки довольно существенно отличаются. В ряде стран даже издают специальные руководства для приезжих водителей.
В США, к примеру, на многих знаках вместо условных обозначений используются надписи, что затрудняет их восприятие. На японских дорожных знаках, которые частично близки к международному стандарту, нередко используются иероглифы.
Некоторые знаки имеют даже свою родину. К примеру, привычный всем знак пешеходного перехода «сочинили» в СССР.
На сегодняшний день в одной только России используется больше 250 дорожных знаков и система постоянно развивается и совершенствуется.
Случались и откровенно забавные моменты: на какое-то время из перечня исчез знак «неровная дорога». Вернули его в список только в 1961 году. С чем было связано его исключение из набора — не ясно. То ли дороги вдруг стали ровные, то ли состояние их было настолько печальным, что особого смысла ставить предупреждение не было.
- Дорожные знаки РФ (ГОСТ Р 52289-2004, ГОСТ Р 52290-2004 и ст. 12.16 КоАП)
- Правила дорожного движения РФ (ГОСТ 10807-78, ГОСТ Р 51582-2000, ГОСТ 23457-86)
- Свободная электронная энциклопедия Википедия, раздел «Дорожный знак».
- Свободная электронная энциклопедия Википедия, раздел «Венская конвенция о дорожных знаках и сигналах».
- Свободная электронная энциклопедия Википедия, раздел «Сравнение дорожных знаков Европы».
Вряд ли среди интернет-аудитории встретится человек, которому незнаком этот символ @.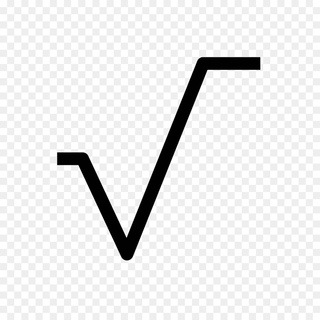
На сетевых просторах он используется в качестве разделителя между именем пользователя и именем хоста в синтаксисе адреса электронной почты.
Некоторые деятели интернет-пространства называют этот символ «одним из главных поп-символов современности, сигнатом нашего общего коммуникационного пространства». Несколько высокопарно, на мой взгляд, но о всемирном признании этого символа, и как даже иногда отмечают, «канонизации» свидетельствует следующий факт.
В феврале 2004 года Международный союз электросвязи ввёл в азбуку Морзе код для символа @ ( — — — ), для удобства передачи адресов электронной почты. Код совмещает латинские буквы А и С и отражает их совместное графическое написание.
Поиски истоков символа @ уводят нас по меньшей мере в XV век, а возможно, еще дальше, хотя лингвисты и палеографы до сих пор расходятся во мнениях по этому вопросу.
Профессор Джорджио Стабиле (Giorgio Stabile) выдвинул такую гипотезу. В документе XVI в., написанном флорентийским купцом, упоминалась «цена одной А вина» (возможно, амфоры).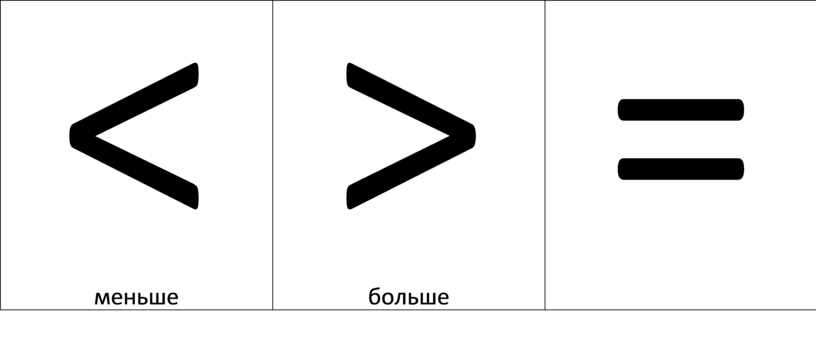
При этом буква А, по тогдашней традиции, была украшена завитком и выглядела как @.
Американский ученый Бертольд Уллман выдвинул предположение, что знак @ был изобретен средневековыми монахами для сокращения латинского слова «ad», которое часто употреблялось в качестве универсального слова, означающего «на», «в», «в отношении» и т.п. В том шрифте, которым пользовались монахи, буква «d» писалась с небольшим хвостиком, и это делало её немного похожей на цифру «6» в зеркальном отражении. Так предлог «ad» стал символом @.
Как бы то ни было, это новшество вскоре переняли торговцы: одним из первых, кто использовал символ вне стен монастыря, был флорентийский купец Франческо Лапи, в одном из своих писем обозначивший «собакой» амфору — стандартную в те времена меру объёма, примерно равную 26-ти л.
В испанском, португальском, французском языках название символа происходит от слова «арроба» – староиспанская мера веса, ок. 15 кг. (по другим данным 11,502 кг), которая сокращённо обозначалась на письме знаком @.
Что касается эпохи Возрождения, то знак @ начали использовать для того, чтобы обозначать цену, но а в эпоху индустриальной революции знак @ начал появляться в отчётах бухгалтеров. Современное официальное название символа «коммерческое at» берёт своё происхождение из счетов, например, 7 widgets @ $2 each = $14, что переводится как 7 шт. по 2$ = 14$. Поскольку этот символ применялся в бизнесе, он был размещён на клавиатурах пишущих машинок и оттуда перекочевал на компьютер.
Распространением данного символа на сетевых просторах мы обязаны праотцу электронной почты Томлинсону. Именно он был тем самым человеком, который выбрал символ @.
Тут нужно немного отвлечься и просветить вас в том, чем занимался Томлинсон и почему именно его принято считать изобретателем электронной почты, а заодно и значка @, хотя на самом деле, он не делал ни того, ни другого. Компания, в которой Томлтнсон работал, примерно в конце 60-х стала участницей проекта ARPANet, компьютерной сети для министерства обороны США.
Именно эта сеть и явилась предшественницей интернета. В те годы уже существовало несколько программ, которые были способны передать файл или послание от одного человека другому. Но отправителю и получателю нужно было пользоваться одним компьютером. Что касается модема, то даже самый быстрый в то время работал раз этак в 200 медленнее современного обычного, который позволяет качать информацию со скоростью 56,6 Кбит/сек.
Томлинсон как раз в то время занимался разработкой почтовой программы и созданием виртуального почтового ящика. На самом деле электронный ящик того времени был файлом, который различался от обычного только одной особенностью — пользователи не имели возможности исправить присланный текст, а только добавить что-то своё. В такой операции использовались только две программы — SNDMSG для того, чтобы отправить файл и READMAIL для того, чтобы его прочитать.
Томлинсон же написал новую программу, которая состояла из кода в 200 строк. Такая программа являла собой нечто среднее между двумя вышеупомянутыми программами и протоколом CPYNET, который был использован в ARPANet для того, чтобы отсылать файлы на удалённый компьютер.
Первое экспериментальное послание Томлинсона было отправлено с одного компьютера в лаборатории на другой.
Для того, чтобы переправить файл Томлинсон затратил примерно полгода, пока не получилось от править послание на компьютер, который действительно можно было считать удалённым.
Конечно, об успехе Томлинсона знали не очень многие, только круг коллег, так как заслугу нигде не освещали.
Ну, а теперь можно вернуться к «собаке». Томлинсон использовал клавиатуру 33 Teletype. И однажды ему понадобился достаточно уникальный символ, который не использовался широко ранее. Такой символ не должен был встречаться ни в одном названии или имени и ещё он должен был разделять имя пользователя и компьютера. Должен был получиться алгоритм по типу имени – символа – места.
Кроме цифр и букв, на клавиатуре были знаки пунктуации, а также и @. Но после 1971 года модель клавиатуры претерпела изменения.
@ была наиболее простым решением такого алгоритма. Как утверждал сам Томлинсон, это был единственный вариант.
Когда уже намного позднее его спросили, почему он выбрал этот конкретный значок, он ответил просто: «Я искал на клавиатуре знак, который не мог встретиться ни в одном имени и вызвать путаницу».
Кликабельно
В 1963-м году появилась кодировка стандарта ASCII, в числе 95-ти печатных знаков которой присутствовала и «собака», а в 1973-м году члены организации «Internet Engineering Taskforce» закрепили использование знака при разделении имени и домена — эту идею в 1971-м году выдвинул программист Рэй Томлинсон.
Такой символ понадобился Томлинсону в тот период, когда он работал над созданием системы сообщений в сети Arpanet (прародительнице Internet). По сути он должен был придумать новую схему адресации, которая бы идентифицировала не только получателей, но и компьютеры, на которых находились их почтовые ящики. Для этого Томлинсону понадобился разделитель, и его, в общем-то, случайный выбор пал на знак @.
Первым сетевым адресом был [email protected] Массовой «собака» стала в 1996-м году, когда появился сервис «Hotmail».
Примерно год спустя после описанных выше событий Винтан Серф и Боб Кан изобрели протокол под названием TCP/IP. И об этом тоже долго упоминалось только в узких кругах.
Вообще, история Интернета довольно свежая, все исторически личности пока живы, поэтому будет справедливо упомянуть людей, которые приложили руку к созданию почты e-mail.
Один из создателей — Дуглас Энгельбарт (вот тут историю этого изобретения ). Он сделал компьютерную мышь и создал первую систему обмена именно текстовыми сообщениями. После этого Томлинсон преподнёс её в виде конверта с полем получателя, отправителя и адреса и текстом письма. После этого программу обрабатывал Лоуренс Робертс, который придумал список писем, чтение письма выборочно и сохранение информации в отдельном файле и пересылку.
Томлинсона, надо отметить, весьма повеселила шумиха, которую развернули на 30-е электронной почты.
Несмотря на ту славу, что обрушилась на него, он производит впечатление обычного человека, хотя и посмеивается над тем, что e-mail по мнению всех остальных, появился за один день.
Да и было это не 30 лет назад. История знака @ — это довольно забавная эпопея, которая связана и с первым посланием. Есть две легенды по этому поводу.
Первая версия о том, что содержалось в историческом первом письме гласила, что Томлинсон набрал QWERTYUIOP – то есть весь верхний ряд букв слева направо. По этому поводу журналисты подняли много шума. Их интересовало, что было написано, и явно ожидали чего-то многозначительного и символического. Так как Томлинсон был персоной отнюдь не публичной, он и не догадался, что мог сказать что угодно.
Он вполне честно ответил о теле письма, так как и не подозревал вовсе, что оно могло получиться историческим. Но ведь журналистам нужны изюминки, а не банальности. Поэтому не очень хотелось сообщать всем, что в письме и вовсе оказался беспорядочный набор букв. Поэтому появился QWERTYUIOP. А инженер и не думает опровергать эту версию.
И вторая версия – это то, что он написал цитату из геттисбергской речи Линкольна. Надо думать, учёный просто во всю подкалывает журналистов и ёрничает, как может. Было бы странно, если бы он на самом деле в каждом экспериментальном письме писал нечто возвышенное. Но эта версия достаточно понравилась журналистам, и они начали её повторять.
В России пользователи чаще всего называют символ «@» «собакой», из-за чего e-mail адреса, образованные от личных имен и фамилий, иногда приобретают непредвиденную окраску. Любопытно, что данный символ используют в своем творчестве как народные таланты (например, шутка: «Пропала собака, @ не предлагать»), так и официальные хохмачи – КВНщики (например, «[email protected]»).
Но все же: почему именно «собака»? Существует несколько версий происхождения этого забавного названия.
Во-первых, значок действительно похож на свернувшуюся калачиком собачку.
Во-вторых – отрывистое звучание английского «at» немного напоминает собачий лай.
В-третьих, при изрядном воображении вы можете рассмотреть в начертаниях символа практически все буквы, входящие в слово «собака», ну разве что, за исключеним «к».
Но самой романтичной является следующая легенда: «Давным-давно, когда компьютеры были большими, а дисплеи – исключительно текстовыми, жила-была популярная игра с немудрящим названием «Adventure» («Приключение»). Смыслом ее было путешествие по созданному компьютером лабиринту в поисках сокровищ и сражения с вредоносными подземными тварями. При этом лабиринт на экране был нарисован символами «!», «+» и «-», а играющий, клады и враждебные монстры обозначались различными буквами и значками. Причем по сюжету у игрока был верный помощник – пес, которого можно было отправлять в катакомбы на разведку. И обозначался он, конечно же, значком @».
Это ли стало первопричиной общепринятого ныне названия, или, наоборот, значок был выбран потому, что уже так назывался, – об этом легенда умалчивает.
Справедливости ради надо отметить, что в России «собака» называется также собачкой, лягушкой, плюшкой, ухом, бараном и даже крякозяброй.
В других странах этот символ ассоциируется с разными предметами.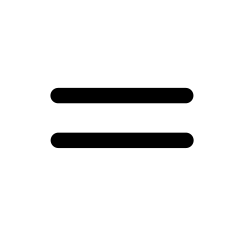
Ниже приведен далеко не полный список того, как называют символ «@» в других странах.
Итальянцы говорят «chiocciola» («улитка»), в Греции его знают, как «παπακι» — «уточка», в Чехии и Словакии — «zavináč» -рольмопс — («рулетик из сельди» или сельдь под маринадом), на Тайване используют понятие «小老鼠» (произносится как «сяо лао шу») — «мышка», в Израиле распространено название «שטרודל» — «штрудель», а в Казахстане знак именуют «айқұлақ» — «ухо Луны».
Болгария – кльомба или маймунско а («обезьяна А»),
Нидерланды – apenstaartje («обезьяний хвостик»),
Испания – как и мера веса «arroba»,
Франция – та же мера веса «arrobase»,
Германия, Польша – обезьяний хвост, обезьянье ухо, скрепка, обезьяна,
Дания, Норвегия, Швеция – «snabel-a» – «рыло а» или слоновый хобот,
Америка, Финляндия – кошка,
Китай, Тайвань – мышонок,
Турция – розочка,
в Сербии – «чокнутая A»,
во Вьетнаме – «скрюченная A»,
на Украине – «равлик» (улитка), «песик» или опять же «собака».
Как видите, у многих народов знак @ вызывает ассоциацию с уютно устроившимся зверьком, у некоторых с аппетитным штруделем или селедочным рулетом, поэтичные турки сравнили с цветком, а вот дисциплинированные японцы используют английское «attomark» без всяких поэтических сравнений.
источники
http://www.factroom.ru/facts/40864#more-40864
http://shkolazhizni.ru/archive/0/n-7999/
http://viva-woman.ru/novosti-so-vsego-sveta/kak-pojavilsja-simvol-sobaka.html
кто придумал первый знак пунктуации? как назывался этот знак? какое у него было назначений?
Пунктуация (от лат. punctus – точка) – знаки, разделяющие слова на удобные для восприятия группы, вносящие порядок в эти группы и помогающие правильно воспринимать или по крайней мере препятствовать ложному толкованию слов и выражений.Однако до середины XVII в. «пунктуацией» называлась простановка точек около согласных для обозначения гласных звуков в тексте на иврите, в то время как написание знаков в латинском тексте называлось простановкой точек.
Где-то около 1650 эти два слова обменялись своими значениями.2000 лет назад простановка точек для разделения текста не существовала, как не существовало и правила разделять слова пробелами. Судя по всему, некоторые греческие писатели использовали отдельные знаки пунктуации уже в V в. до н. э. Например, драматург Еврипид отмечал перемену говорящего лица остроконечным знаком, а философ Платон иногда заканчивал раздел книги двоеточием.
Первый знак пунктуации был изобретен Аристотелем (384–322 до н. э.) для того, чтобы обозначить изменение смыслового значения. Он назывался параграфос (запись на стороне) и представлял собой короткую горизонтальную линию внизу у начала строчки. В I в. римляне, уже пользовавшиеся точками, стали отмечать параграфы тем, что писали на полях несколько первых букв нового раздела. В позднем Средневековье на этом месте стали ставить букву «с» как сокращение слова capitulum (глава). Как уже отмечалось выше, современная практика разделения параграфов в виде отступов и пропуска строки была принята только в XVII в.
Применение знаков для разделения малых смысловых отрезков текста началось примерно в 194 до н. э., когда грамматик Аристофан Александрийский изобрел трехточную систему для разбивки текста на большие по размеру, средние и малые отрезки. Так, точку, стоящую внизу и называемую «комма», он ставил в конце самого короткого отрезка, точка вверху (периодос) делила текст на большие отрезки, а точка в середине (колон) – на средние. Вероятно, что именно Аристофан ввел дефис, чтобы писать составные слова, и наклонную черту, которую ставил около слов с неясным значением.
Хотя все эти нововведения не получили широкого распространения, они спорадически использовались до VIII в. К этому времени писцы стали разделять слова в предложении, а также использовать прописные буквы. Так как с буквами, меняющими размер, читать текст без знаков пунктуации оказалось довольно неудобно, англосаксонский ученый Алкуин (735–804), руководивший придворной школой в Аахене (Германия), несколько реформировал систему Аристофана, сделав ряд добавлений.
Некоторые из них дошли до Англии, где к X в. знаки пунктуации появились в манускриптах для обозначения паузы и изменения интонации.Впервые же пунктуационные знаки, в том виде, в котором они сохранились до наших дней, были введены в конце XV в. венецианским печатником Альдом Мануцием. Именно его книги проложили дорогу большинству знаков, употребляемых в наши дни, – точке, точке с запятой и двоеточию. Спустя 60 лет внук печатника Альд Мануций Младший впервые определил роль знаков пунктуации как вспомогательных для определения структуры предложения.
Этот символ знаком любому пользователю интернета. Но появился он отнюдь не в век всеобщей компьютерной грамотности, символ который мы называем «собака» был известен еще в средние века, и у него было несколько разных назначений. Версий его происхождения тоже несколько, все они интересны и заслуживают внимания.
Символ @ известен как минимум с XV века , но вполне возможно, что он был придуман и раньше. До сих пор доподлинно не установлено, как и откуда он появился, и время первого упоминания определено лишь приблизительно.
По одной из версий, знак @ первыми стали использовать в письме монахи, делавшие переводы трактатов, которые были написаны в том числе и на латыни. В латыни есть предлог «ad», и в шрифте принятом в то время для письма, буква «d» писалась с небольшим хвостиком, закрученным вверх. При быстром письме предлог выглядел как значок @.
Благодаря флорентийским купцам, с XV века значок @ стал использоваться в качестве коммерческого символа. Он обозначал меру веса, равную 12,5 кг. – амфору, и по тогдашней традиции буква «А», которой и обозначался вес, была украшена завитками и выглядела как всем известный сегодня символ. У испанцев, португальцев и французов своя версия происхождения обозначения – от слова «арроба» — староиспанской меры веса около 15 кг, которую обозначали в письме условным знаком @, тоже взятом от первой буквы слова.
В современном коммерческом языке официальное название знака @ — «коммерческое at» произошло из бухгалтерских счетов, где обозначало предлог «в, на, по, к», и в русском переводе выглядело примерно так – 5шт.
по 3$ (5 widgets @ $3 each). Так как символ использовался в торговле, то он был размещен на клавиатурах первых пишущих машинок, откуда и перебрался на компьютерную клавиатуру.
В интернете символ @ появился благодаря создателю электронной почты Томлинсону. Почему он выбрал этот знак для разделения имени пользователя и сервера электронной почты Томлинсон объяснил просто – он искал знак, который бы не встречался ни в именах, ни в названиях и не мог внести путаницу в систему. В разных странах символ называют по-разному, как собачка он известен лишь в русском языке. Версий появления этого забавного названия несколько. Согласно одной из них – звучание английского «at» напоминает собачий лай, по другой – сам значок напоминает свернувшуюся калачиком маленькую собачку. Но самая популярная связана с одной из первых текстовых игр. По сюжету, у игрока был помощник, верный пес, который помогал искать клады, защищал от разных монстров, отправлялся в разведку и в катакомбы. И конечно же обозначался пес знаком @.
Кстати, символ @ во многих странах так или иначе пользователи связывают с животными – у немцев и поляков это обезьянка, у итальянцев – улитка, в Америке и Финляндии – кошка, на Тайване и в Китае – мышка. В других странах символ означает что-то вкусное – булочку с корицей у шведов, штрудель у израильтян. Только дисциплинированные японцы далеки от романтичных сравнений и предпочитают называть знак «attomark», так как он звучит в английском языке, и не придумывают для него своих названий.
| Специальные символы | ||
| Символ | Код | Описание |
| ∀ | 8704 | Для любого |
| ∃ | 8707 | Существует |
| Ø | 216 | Пустое множество |
| ∈ | 8712 | Принадлежит |
| ∉ | 8713 | Не принадлежит |
| ∋ | 8727 | Содержит |
| ⊂ | 8834 | Является подмножеством |
| ⊃ | 8835 | Является надмножеством |
| ⊄ | 8836 | Не является подмножеством |
| ⊆ | 8838 | Является подмножеством либо равно |
| ⊇ | 8839 | Является надмножеством либо равно |
| ∩ | 8745 | Пересечение |
| ∪ | 8746 | Объединение |
| ∧ | 8743 | Логическое И |
| ∨ | 8744 | Логическое ИЛИ |
| ¬ | 172 | Отрицание |
| ≤ | 8804 | Меньше или равно |
| ≥ | 8805 | Больше или равно |
| ≠ | 8800 | Не равно |
| ≈ | 8776 | Приблизительно равно |
| ≡ | 8801 | Тождественно |
| ∞ | 8734 | Бесконечность |
| ± | 177 | Плюс/минус |
| ⁄ | 8260 | Дробная черта |
| − | 8722 | Минус |
| · | 183 | Произведение-точка |
| × | 215 | Произведение-крестик |
| ÷ | 247 | Деление |
| ○ | 9675 | Композиция |
| √ | 8730 | Квадратный корень |
| ⊕ | 8853 | Плюс в кружке |
| ⊗ | 8855 | Знак умножения в кружке |
| ← | 8592 | Стрелка влево |
| ↑ | 8593 | Стрелка вверх |
| → | 8594 | Стрелка вправо |
| ↔ | 8596 | Стрелка влево и вправо |
| ⇐ | 8656 | Двойная стрелка влево |
| ⇒ | 8658 | Двойная стрелка вправо |
| ⇔ | 8660 | Двойная стрелка влево и вправо |
| ° | 176 | Градус |
| ⊥ | 8869 | Перпендикулярно |
| ∠ | 8736 | Угол |
| ∂ | 8706 | Частичная производная / граница |
| ∫ | 8747 | Интеграл |
| ¹ | 185 | Степень 1 |
| ² | 178 | Степень 2 |
| ³ | 179 | Степень 3 |
| ½ | 189 | Одна вторая |
| ∑ | 8721 | Знак суммирования |
| ∏ | 8719 | Знак произведения |
Прошлое и будущее / Блог компании Wolfram Research / Хабр
Перевод поста Стивена Вольфрама (Stephen Wolfram) «Mathematical Notation: Past and Future (2000)».
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации
Содержание
Резюме
Введение
История
Компьютеры
Будущее
Примечания
— Эмпирические законы для математических обозначений
— Печатные обозначения против экранных
— Письменные обозначения
— Шрифты и символы
— Поиск математических формул
— Невизуальные обозначения
— Доказательства
— Отбор символов
— Частотное распределение символов
— Части речи в математической нотации
Стенограмма речи, представленной на секции «MathML и математика в сети» первой Международной Конференции MathML в 2000-м году.
Большинство математических обозначений существуют уже более пятисот лет. Я рассмотрю, как они разрабатывались, что было в античные и средневековые времена, какие обозначения вводили Лейбниц, Эйлер, Пеано и другие, как они получили распространение в 19 и 20 веках. Будет рассмотрен вопрос о схожести математических обозначений с тем, что объединяет обычные человеческие языки.
Я расскажу об основных принципах, которые были обнаружены для обычных человеческих языков, какие из них применяются в математических обозначениях и какие нет.Согласно историческим тенденциям, математическая нотация, как и естественный язык, могла бы оказаться невероятно сложной для понимания компьютером. Но за последние пять лет мы внедрили в Mathematica возможности к пониманию чего-то очень близкого к стандартной математической нотации. Я расскажу о ключевых идеях, которые сделали это возможным, а также о тех особенностях в математических обозначениях, которые мы попутно обнаружили.
Большие математические выражения — в отличии от фрагментов обычного текста — часто представляют собой результаты вычислений и создаются автоматически. Я расскажу об обработке подобных выражений и о том, что мы предприняли для того, чтобы сделать их более понятными для людей.
Традиционная математическая нотация представляет математические объекты, а не математические процессы. Я расскажу о попытках разработать нотацию для алгоритмов, об опыте реализации этого в APL, Mathematica, в программах для автоматических доказательств и других системах.
Обычный язык состоит их строк текста; математическая нотация часто также содержит двумерные структуры. Будет обсуждён вопрос о применении в математической нотации более общих структур и как они соотносятся с пределом познавательных возможностей людей.
Сфера приложения конкретного естественного языка обычно ограничивает сферу мышления тех, кто его использует. Я рассмотрю то, как традиционная математическая нотация ограничивает возможности математики, а также то, на что могут быть похожи обобщения математики.
Когда собиралась эта конференция, люди подумали, что было бы здорово пригласить кого-то для выступления с речью об основаниях и общих принципах математической нотации. И был очевидный кандидат — Флориан Каджори — автор классической книги под названием «История математических обозначений». Но после небольшого расследования оказалось, что есть техническая проблема в приглашении доктора Каджори — он умер как минимум лет семьдесят назад.
Так что мне придётся его заменять.
Полагаю, других вариантов особо-то и не было. Поскольку оказывается, что нет почти никого, кто жив на данный момент и кто занимался фундаментальными исследованиями математической нотации.
В прошлом математической нотацией занимались обычно в контексте систематизации математики. Так, Лейбниц и некоторые другие люди интересовались подобными вещами в середине 17 века. Бэббидж написал тяжеловесный труд по этой теме в 1821 году. И на рубеже 19 и 20 веков, в период серьёзного развития абстрактной алгебры и математической логики, происходит очередной всплеск интереса и деятельности в этой теме. Но после этого не было почти ничего.
Однако не особо удивительно, что я стал интересоваться подобными вещами. Потому что с Mathematica одной из моих главных целей было сделать ещё один большой шаг в области систематизации математики. А более общей моей целью в отношении Mathematica было распространить вычислительную мощь на все виды технической и математической работы. Эта задача имеет две части: то, как вычисления происходят внутри, и то, как люди направляют эти вычисления для получения того, что они хотят.
Одно из самых больших достижений Mathematica, о котором, вероятно, большинство из вас знает, заключается в сочетании высокой общности вычислений изнутри и сохранении практичности, основанной на преобразованиях символьных выражений, где символьные выражения могут представлять данные, графику, документы, формулы — да что угодно.
Однако недостаточно просто проводить вычисления. Необходимо так же, чтобы люди каким-то образом сообщали Mathematica о том, какие вычисления они хотят произвести. И основной способ дать людям взаимодействовать с чем-то столь сложным — использовать что-то вроде языка.
Обычно языки появляются в ходе некоторого поэтапного исторического процесса. Но компьютерные языки в историческом плане сильно отличаются. Многие были созданы практически полностью разом, зачастую одним человеком.
Так что включает в себя эта работа?
Ну, вот в чём заключалась для меня эта работа в отношении Mathematica: я попробовал представить, какие вообще вычисления люди будут производить, какие фрагменты в этой вычислительной работе повторяются снова и снова.
А затем, собственно, я дал имена этим фрагментам и внедрил в качестве встроенных функций в Mathematica.
В основном мы отталкивались от английского языка, так как имена этих фрагментов основаны на простых английских словах. То есть это значит, что человек, который просто знает английский, уже сможет кое-что понять из написанного в Mathematica.
Однако, разумеется, язык Mathematica — не английский. Это скорее сильно адаптированный фрагмент английского языка, оптимизированный для передачи информации о вычислениях в Mathematica.
Можно было бы думать, что, пожалуй, было бы неплохо объясняться с Mathematica на обычном английском языке. В конце концов, мы уже знаем английский язык, так что нам было бы необязательно изучать что-то новое, чтобы объясняться с Mathematica.
Однако я считаю, что есть весьма весомые причины того, почему лучше думать на языке Mathematica, чем на английском, когда мы размышляем о разного рода вычислениях, которые производит Mathematica.
Однако мы так же знаем, заставить компьютер полностью понимать естественный язык — задача крайне сложная.
Хорошо, так что насчёт математической нотации?
Большинство людей, которые работают в Mathematica, знакомы по крайней мере с некоторыми математическими обозначениями, так что, казалось бы, было бы весьма удобно объясняться с Mathematica в рамках привычной математической нотации.
Но можно было бы подумать, что это не будет работать. Можно было бы подумать, что ситуация выльется в нечто, напоминающее ситуацию с естественными языками.
Однако есть один удивительный факт — он весьма удивил меня. В отличие от естественных человеческих языков, для обычной математической нотации можно сделать очень хорошее приближение, которое компьютер сможет понимать. Это одна из самых серьёзных вещей, которую мы разработали для третьей версии Mathematica в 1997 году [текущая версия Wolfram Mathematica — 10.4.1 — вышла в апреле 2016 г. — прим. ред.]. И как минимум некоторая часть того, что у нас получилось, вошла в спецификацию MathML.
Сегодня я хочу поговорить о некоторых общих принципах в математической нотации, которые мне довелось обнаружить, и то, что это означает в контексте сегодняшних дней и будущего.
В действительности, это не математическая проблема. Это куда ближе к лингвистике. Речь не о том, какой бы могла быть математическая нотация, а о том, какова используемая математическая нотация в действительности — как она развивалась в ходе истории и как связана с ограничениями человеческого познания.
Я думаю, математическая нотация — весьма интересное поле исследования для лингвистики.
Как можно было заметить, лингвистика в основном изучала разговорные языки. Даже пунктуация осталась практически без внимания. И, насколько мне известно, никаких серьёзных исследований математической нотации с точки зрения лингвистики никогда не проводилось.
Обычно в лингвистике выделяют несколько направлений. В одном занимаются вопросами исторических изменений в языках. В другом изучается то, как влияет изучение языка на отдельных людей.
В третьем создаются эмпирические модели каких-то языковых структур.
Давайте сперва поговорим об истории.
Откуда произошли все те математические обозначения, которые мы в настоящее время используем?
Это тесно связано с историей самой математики, так что нам придётся коснуться немного этого вопроса. Часто можно услышать мнение, что сегодняшняя математика есть единственная мыслимая её реализация. То, какими бы могли быть произвольные абстрактные построения.
И за последние девять лет, что я занимался одним большим научным проектом, я ясно понял, что такой взгляд на математику не является верным. Математика в том виде, в котором она используется — это учение не о произвольных абстрактных системах. Это учение о конкретной абстрактной системе, которая исторически возникла в математике. И если заглянуть в прошлое, то можно увидеть, что есть три основные направления, из которых появилась математика в том виде, в котором мы сейчас её знаем — это арифметика, геометрия и логика.
Все эти традиции довольно стары. Арифметика берёт своё начало со времён древнего Вавилона. Возможно, и геометрия тоже приходит из тех времён, но точно уже была известна в древнем Египте. Логика приходит из древней Греции.
И мы можем наблюдать, что развитие математической нотации — языка математики — сильно связано с этими направлениями, особенно с арифметикой и логикой.
Следует понимать, что все три направления появлялись в различных сферах человеческого бытия, и это сильно повлияло на используемые в них обозначения.
Арифметика, вероятно, возникла из нужд торговли, для таких вещей, как, к примеру, счёт денег, а затем арифметику подхватили астрология и астрономия. Геометрия, по всей видимости, возникла из землемерческих и подобных задач. А логика, как известно, родилась из попытки систематизировать аргументы, приведённые на естественном языке.
Примечательно, кстати, что другая, очень старая область знаний, о которой я упомяну позднее — грамматика — по сути никогда не интегрировалась с математикой, по крайней мере до совсем недавнего времени.
Итак, давайте поговорим о ранних традициях в обозначениях в математике.
Во-первых, есть арифметика. И самая базовая вещь для арифметики — числа. Так какие обозначения использовались для чисел?
Что ж, первое представление чисел, о котором доподлинно известно — высечки на костях, сделанные 25 тысяч лет назад. Это была унарная система: чтобы представить число 7, нужно было сделать 7 высечек, ну и так далее.
Конечно, мы не можем точно знать, что именно это представление чисел было самым первым. Я имею ввиду, что мы могли и не найти свидетельств каких-то других, более ранних представлений чисел. Однако, если кто-то в те времена изобрёл какое-то необычное представление для чисел, и разместил их, к примеру, в наскальной живописи, то мы можем никогда и не узнать, что это было представление чисел — мы можем воспринимать это просто как какие-то фрагменты украшений.
Таким образом, числа можно представлять в унарной форме. И такое впечатление, что эта идея возрождалась множество раз и в различных частях света.
Но если посмотреть на то, что произошло помимо этого, то можно обнаружить довольно много различий. Это немного напоминает то, как различные виды конструкций для предложений, глаголов и прочее реализованы в различных естественных языках.
И, фактически, один из самых важных вопросов относительно чисел, который, как я полагаю, будет всплывать ещё много раз — насколько сильным должно быть соответствие между обычным естественным языком и языком математики?
Или вот вопрос: он связан с позиционной нотацией и повторным использованием цифр.
Как можно заметить, в естественных языках обычно есть такие слова, как «десять«, «сто«, «тысяча«, «миллион» и так далее. Однако в математике мы можем представить десять как «один нуль» (10), сто как «один нуль нуль» (100), тысячу как «один нуль нуль нуль» (1000) и так далее. Мы можем повторно использовать эту одну цифру и получать что-то новое, в зависимости от того, где в числе она будет появляться.
Что ж, это сложная идея, и людям потребовались тысячи лет, чтобы её действительно принять и осознать. А их неспособность принять её ранее имела большие последствия в используемых ими обозначениях как для чисел, так и для других вещей.
Как это часто бывает в истории, верные идеи появляются очень рано и долгое время остаются в забвении. Более пяти тысяч лет назад вавилоняне, и возможно даже до них ещё и шумеры разработали идею о позиционном представлении чисел. Их система счисления была шестидесятеричная, а не десятичная, как у нас. От них мы унаследовали представление секунд, минут и часов в существующей ныне форме. Но у них была идея использования одних и тех же цифр для обозначения множителей различных степеней шестидесяти.
Вот пример их обозначений.
Из этой картинки можно понять, почему археология столь трудна. Это очень маленький кусок обожжённой глины. Было найдено около полумиллиона подобных вавилонских табличек. И примерно одна из тысячи — то есть всего около 400 — содержат какие-то математические записи. Что, кстати, выше отношения математических текстов к обычным в современном интернете. Вообще, пока MathML не получил достаточного распространения, это является достаточно сложным вопросом.
Но, в любом случае, маленькие обозначения на этой табличке выглядят слегка похожими на отпечатки лапок крошечных птиц. Но почти 50 лет назад в конце концов исследователи определили, что эта клинописная табличка времён Хаммурапи — около 1750 года до н.э. — фактически является таблицей того, что мы сейчас называем пифагорейскими тройками.
Что ж, эти вавилонские знания были утеряны для человечества почти на 3000 лет. И вместо этого использовались схемы, основанные на естественных языках, с отдельными символами для десяти, ста и так далее.
Так, к примеру, у египтян для обозначения тысячи использовался символ цветка лотоса, для сотни тысяч — птица, ну и так далее. Каждая степень десяти для её обозначения имела отдельный символ.
А затем появилась другая очень важная идея, до которой не додумались ни вавилоняне, ни египтяне. Она заключалась в обозначении чисел цифрами — то есть не обозначать число семь семью единицами чего-то, а лишь одним символом.
Однако, у греков, возможно, как и у финикийцев ранее, эта идея уже была. Ну, на самом деле, она была несколько отличной. Она заключалась в том, чтобы обозначать последовательность чисел через последовательность букв в их алфавите. То есть альфе соответствовала единица, бете — двойка и так далее.
Вот как выглядит список чисел в греческом обозначении [вы можете скачать Wolfram Language Package, позволяющий представить числа в различных древних нотациях здесь — прим. ред.].
(Думаю, именно так сисадмины из Академии Платона адаптировали бы свою версию Mathematica; их воображаемую -600-ю (или около того) версию Mathematica.)
С этой системой счисления сопряжено множество проблем. Например, есть серьёзная проблема управления версиями: даже если вы решаете удалить какие-то буквы из своего алфавита, то вы должны оставить их в числах, иначе все ваши ранее записанные числа будут некорректными.
То есть это значит, что есть различные устаревшие греческие буквы, оставшиеся в системе счисления — как коппа для обозначения числа 90 и сампи для обозначения числа 900. Однако я включил их в набор символов для Mathematica, потому здесь прекрасно работает греческая форма записи чисел.
Спустя некоторое время римляне разработали свою форму записи чисел, с которой мы хорошо знакомы.
Пускай сейчас и не совсем ясно, что их цифры изначально задумывались как буквы, однако об этом следует помнить.
Итак, давайте попробуем римскую форму записи чисел.
Это тоже довольно неудобный способ записи, особенно для больших чисел.
Тут есть несколько интересных моментов. К примеру, длина представляемого числа рекурсивно возрастает с размером числа.
И в целом, подобное представление для больших чисел полно неприятных моментов. К примеру, когда Архимед писал свою работу о количестве песчинок, объём которых эквивалентен объёму вселенной (Архимед оценил их количество в 1051, однако, полагаю, правильный ответ будет около 1090), то он использовал обычные слова вместо обозначений, чтобы описать столь большое число.
Но на самом деле есть более серьёзная понятийная проблема с идеей о представлении цифр как букв: становится трудно придумать представление символьных переменных — каких-то символьных объектов, за которыми стоят числа. Потому что любую букву, которую можно было бы использовать для этого символьного объекта, можно будет спутать с цифрой или фрагментом числа.
Общая идея о символьном обозначении каких-то объектов через буквы известна довольно давно. Евклид, по сути, использовал эту идею в своих трудах по геометрии.
К сожалению, не сохранилось оригиналов работ Евклида. Однако имеются на несколько сот лет более молодые версии его работ. Вот одна, написанная на греческом языке.
И на этих геометрических фигурах можно увидеть точки, которые имеют символьное представление в виде греческих букв. И в описании теорем есть множество моментов, в которых точки, линии и углы имеют символьное представление в виде букв. Так что идея о символьном представлении каких-то объектов в виде букв берёт своё начало как минимум от Евклида.
Однако эта идея могла появиться и раньше. Если бы я умел читать на вавилонском, я бы, вероятно, смог бы сказать вам точно. Вот вавилонская табличка, в которой представляется квадратный корень из двух, и которая использует вавилонские буквы для обозначений.
Полагаю, обожжённая глина более долговечна, чем папирус, и получается, что мы знаем о том, что писали вавилоняне больше, чем о том, что писали люди вроде Евклида.
Вообще, эта неспособность увидеть возможность вводить имена для числовых переменных есть интересный случай, когда языки или обозначения ограничивают наше мышление. Это то, что несомненно обсуждается в обычной лингвистике. В наиболее распространённой формулировке эта идея звучит как гипотеза Сепира-Уорфа (гипотеза лингвистической относительности).
Разумеется, для тех из нас, кто потратил некоторую часть своей жизни на разработку компьютерных языков, эта идея представляется очень важной. То есть я точно знаю, что если я буду думать на языке Mathematica, то многие концепции будут достаточно просты для моего понимания, и они будут совсем не такими простыми, если я буду думать на каком-то другом языке.
Но, в любом случае, без переменных всё было бы гораздо сложнее. Например, как вы представите многочлен?
Ну, Диофант — тот самый, что придумал диофантовы уравнения — сталкивался с проблемой представления многочленов в середине 2 века н.э. В итоге он пришёл к использованию определённых основанных на буквах имён для квадратов, кубов и прочего. Вот как это работало.
По крайней мере сейчас нам показалось бы чрезвычайно трудным понять обозначения Диофанта для полиномов. Это пример не очень хороших обозначений. Полагаю, главная причина, помимо ограниченной расширяемости, состоит в том, что эти обозначения делают математические связи между полиномами неочевидными и не выделяют наиболее интересные нам моменты.
Есть и другие схемы задания полиномов без переменных, как, например, китайская схема, которая включала создание двухмерного массива коэффициентов.
Проблема здесь, опять-таки, в расширяемости. И эта проблема с основанными на графике обозначениями всплывает снова и снова: лист бумаги, папирус или что бы то ни было — они все ограничены двумя измерениями.
Хорошо, так что насчёт буквенного обозначения переменных?
Полагаю, что они могли бы появиться лишь после появления чего-то похожего на нашу современную нотацию. И она до определённого времени не появлялась. Были какие-то намёки в индо-арабских обозначениях в середине первого тысячелетия, однако установилось всё лишь к его концу. А на запад эта идея пришла лишь с работой Фибоначчи о вычислениях в 13 веке.
Фибоначчи, разумеется, был тем самым, кто говорил о числах Фибоначчи применительно к задаче о кроликах, однако в действительности эти числа известны были уже более тысячи лет, и служили они для описания форм индийской поэзии. И я всегда находил случай с числами Фибоначчи удивительным и отрезвляющим эпизодом в истории математики: возникнув на заре западной математики, столь привычные и фундаментальные, они начали становиться популярными лишь в 80-е.
В любом случае, также интересно заметить, что идея разбивки цифр в группы по три, чтобы сделать большие числа более читаемыми, имеется уже в книге Фибоначчи 1202 года, хотя я думаю, что он говорил об использовании скобок над числами, а не о разделяющих запятых.
После Фибоначчи наше современное представление для чисел постепенно становится всё популярнее, и ко времени начала книгопечатания в 15 веке оно уже было универсальным, хотя ещё и оставались несколько чудных моментов.
Но алгебраических переменных в полном их смысле тогда ещё не было. Они появились лишь после Виета в конце 16 века и обрели популярность лишь в 17 веке. То есть у Коперника и его современников их ещё не было. Как в основном и у Кеплера. Эти учёные для описания каких-то математических концепций использовали обычный текст, иногда структурированный как у Евклида.
Кстати, даже несмотря на то, что математическая нотация в те времена была не очень хорошо проработана, системы символьных обозначений в алхимии, астрологии и музыке были довольно развиты. Так, к примеру, Кеплер в начале 17 века использовал нечто, похожее на современную музыкальную нотацию, объясняя свою «музыку сфер» для отношений планетарных орбит.
Со времён Виета буквенные обозначения для переменных стали привычным делом. Обычно, кстати, он использовал гласные для неизвестных и согласные — для известных.
Вот как Виет записывал многочлены в форме, которую он называл «zetetics«, а сейчас мы бы это назвали просто символьной алгеброй:
Можно увидеть, что он использует слова для обозначения операций, в основном так, чтобы их нельзя было спутать с переменными.
Так как раньше представляли операции, в каком виде?
Идея о том, что операции есть нечто, что можно в какой-то форме представить, добиралась до умов людей довольно долго. Вавилоняне обычно не использовали символы для операций — для сложения они просто записывали слагаемые друг за другом. И в целом они были предрасположены записывать всё в виде таблиц, так что им не требовалось как-то обозначать операции.
У египтян были некоторые обозначения для операций: для сложения они использовали пару идущих вперёд ног, а для вычитания — идущих назад.
А современный знак +, который, вероятно, является сокращением от «et» на латыни (означает «и»), появился лишь в конце 15 века.
А вот кое-что из 1579 года, что выглядит весьма современным, написанное в основном на английском, пока не начнёшь понимать, что те забавные загогулины — это не иксы, а специальные небуквенные символы, которые представляют различные степени для переменных.
В первой половине 17 века произошла своего рода революция в математической нотации, после которой она практически обрела свой современный вид. Было создано современное обозначение квадратного корня, который ранее обозначался как Rx — это обозначение сейчас используется в медицинских рецептах. И в основном алгебраическая нотация приобрела свой современный вид.
Уильям Отред был одним из тех людей, кто серьёзно занимался этим вопросом. Изобретение логарифмической линейки — одна из вещей, которая сделала его известным. На самом деле о нём практически ничего неизвестно. Он не был крупным математиком, однако сделал много полезного в области преподавания, с такими людьми, как Кристофер Рен и его учениками. Странно, что я ничего не слышал о нём в школе, особенно если учесть, что мы учились в одной и той же школе, только он на 400 лет ранее. Однако изобретение логарифмической линейки было недостаточным для того, чтобы увековечить своё имя в истории математики.
Но, в любом случае, он серьёзно занимался нотацией. Он придумал обозначать умножение крестиком, и он продвинул идею о представлении алгебры посредством обозначений вместо слов — так, как это делал Виет. И, фактически, он изобрёл довольно много других обозначений, подобно тильде для таких предикатов, как IntegerQ.
После Отреда и его сотоварищей эти обозначения быстро установились. Были и альтернативные обозначения, как изображения убывающей и растущей лун для обозначения арифметических операций — прекрасный пример плохого и нерасширяемого дизайна. Однако в основном использовались современные обозначения.
Вот пример.
Это фрагмент рукописи Ньютона Principia, из которой ясно, что он в основном использовал современные алгебраические обозначения. Думаю, именно Ньютон придумал использовать отрицательные степени вместо дробей для обратных величин и прочего. Principia содержит весьма мало обозначений, за исключением этих алгебраических вещей и представления разного материала в стиле Евклида. И в действительности Ньютон не особо интересовался обозначениями. Он даже хотел использовать точечные обозначения для своих флюксий.
Чего не скажешь о Лейбнице. Лейбниц много внимания уделял вопросам нотации. В действительности, он считал, что правильные обозначения есть ключ ко многим человеческим вопросам. Он был своего рода дипломат-аналитик, курсирующий между различными странами, со всеми их различными языками, и т.д. У него была идея, что если создать некий универсальный логический язык, то тогда все люди смогли бы понимать друг друга и имели бы возможность объяснить всё что угодно.
Были и другие люди, которые размышляли о подобном, преимущественно с позиции обычных естественных языков и логики. Один из примеров — довольно специфичный персонаж по имени Раймонд Лул, живший в 14 веке, который заявлял, что изобрёл некие логические колёса, дающие ответы на все вопросы мира.
Но так или иначе, Лейбниц разработал те вещи, которые были интересны и с позиций математики. То, что он хотел сделать, должно было так или иначе объединить все виды обозначений в математике в некоторый точный естественный язык с подобным математике способом описания и решения различных проблем, или даже больше — объединить ещё и все используемые естественные языки.
Ну, как и многие другие свои проекты, Лейбниц так и не воплотил это в жизнь. Однако он занимался самыми разными направлениями математики и серьёзно относился к разработке обозначений для них. Наиболее известные его обозначения были введены им в 1675 году. Для обозначения интегралов он использовал «omn.«, возможно, как сокращение от omnium. Но в пятницу 29 октября 1675 года он написал следующее.
На этом фрагменте бумаги можно увидеть знак интеграла. Он задумывал его как вытянутую S. Несомненно, это и есть современное обозначение интеграла. Ну, между обозначениями интегралов тогда и сейчас почти нет никакой разницы.
Затем в четверг 11 ноября того же года он обозначил дифференциал как «d«. На самом деле, Лейбниц считал это обозначение не самым лучшим и планировал придумать ему какую-нибудь замену. Но, как мы все знаем, этого не произошло.
Что ж, Лейбниц вёл переписку касательно обозначений с самыми разными людьми. Он видел себя кем-то вроде председателя комитета стандартов математических обозначений — так бы мы сказали сейчас. Он считал, что обозначения должны быть максимально краткими. К примеру, Лейбниц говорил: «Зачем использовать две точки для обозначения деления, когда можно использовать лишь одну?«.
Некоторые из продвигаемых им идей так и не получили распространения. К примеру, используя буквы для обозначения переменных, он использовал астрономические знаки для обозначения выражений. Довольно интересная идея, на самом деле.
Так он обозначал функции.
Помимо этих моментов и некоторых исключений наподобие символа пересечения квадратов, который Лейбниц использовал для обозначения равенства, его обозначения практически неизменными дошли до наших дней.
В 18 веке Эйлер активно пользовался обозначениями. Однако, по сути, он следовал по пути Лейбница. Полагаю, он был первым, кто всерьёз начал использовать греческие буквы наравне с латинскими для обозначения переменных.
Есть и некоторые другие обозначения, которые появились вскоре после Лейбница. Следующий пример из книги, вышедшей через несколько лет после смерти Ньютона. Это учебник алгебры, и он содержит весьма традиционные алгебраические обозначения, уже в печатном виде.
А вот книга Лопиталя, напечатанная примерно в то же время, в которой уже практически современная алгебраическая нотация.
И, наконец, вот пример от Эйлера, содержащий весьма современные обозначения для интегралов и прочего.
Эйлер — популяризировал современное обозначение для числа пи, которое первоначально было предложено Уильямом Джонсом, который рассматривал его как сокращение от слова периметр.
Предложенная Лейбницем и сотоварищами нотация довольно долго оставалась неизменной. Происходили небольшие изменения, как, к примеру квадрат x x получил написание x2. Однако практически ничего нового не появилось.
Однако в конце 19 века наблюдается новый всплеск интереса к математической нотации, сопряжённый с развитием математической логики. Были некоторые нововведения, сделанные физиками, такими как Максвелл и Гиббс, в основном для векторов и векторного анализа, как следствие развития абстрактной алгебры. Однако наиболее значимые изменения были сделаны людьми, начиная с Фреге и приблизительно с 1879 года, которые занимались математической логикой.
Эти люди в своих устремлениях были близки к Лейбницу. Они хотели разработать нотацию, которая представляла бы не только математические формулы, но и математические выводы и доказательства. В середине 19 века Буль показал, что основы логики высказываний можно представлять в терминах математики. Однако Фреге и его единомышленники хотели пойти дальше и представить так как логику высказываний, так и любые математические суждения в соответствующих математических терминах и обозначениях.
Фреге решил, что для решения этой задачи потребуются графические обозначения. Вот фрагмент его так называемой «концептуальной нотации«.
К сожалению, в ней трудно разобраться. И в действительности, если посмотреть на историю обозначений в целом, то часто можно встретить попытки изобретения графических обозначений, которые оказывались трудными для понимания. Но в любом случае, обозначения Фреге уж точно не стали популярными.
Потом был Пеано, самый главный энтузиаст в области математической нотации. Он делал ставку на линейное представление обозначений. Вот пример:
Вообще говоря, в 80-х годах 19 века Пеано разработал то, что очень близко к обозначениям, которые используются в большинстве современных теоретико-множественных концепций.
Однако, как и Лейбниц, Пеано не желал останавливаться лишь на универсальной нотации для математики. Он хотел разработать универсальный язык для всего. Эта идея реализовалась у него в то, что он назвал интерлингва — язык на основе упрощённой латыни. Затем он написал нечто вроде краткого изложения математики, назвав это Formulario Mathematico, которое было основано на его обозначениях для формул, и труд этот был написал на этой производной от латыни — на интерлингве.
Интерлингва, подобно эсперанто, который появился примерно в это же время, так и не получил широкого распространения. Однако этого нельзя сказать об обозначениях Пеано. Сперва о них никто ничего толком и не слышал. Но затем Уайтхед и Рассел написали свой труд Principia Mathematica, в котором использовались обозначения Пеано.
Думаю, Уайтхед и Рассел выиграли бы приз в номинации «самая насыщенная математическими обозначениями работа, которая когда-либо была сделана без помощи вычислительных устройств«. Вот пример типичной страницы из Principia Mathematica.
У них были все мыслимые виды обозначений. Частая история, когда авторы впереди своих издателей: Рассел сам разрабатывал шрифты для многих используемых им обозначений.
И, разумеется, тогда речь шла не о шрифтах TrueType или о Type 1, а о самых настоящих кусках свинца. Я о том, что Рассела можно было встретить с тележкой, полной свинцовых оттисков, катящему её в издательство Кембриджского университета для обеспечения корректной вёрстки его книг.
Но, несмотря на все эти усилия, результаты были довольно гротескными и малопонятными. Я думаю, это довольно ясно, что Рассел и Уайтхед зашли слишком далеко со своими обозначениями.
И хотя область математической логики немного прояснилась в результате деятельности Рассела и Уайтхеда, она всё ещё остаётся наименее стандартизированной и содержащей самую сложную нотацию.
Но что насчёт более распространённых составляющих математики?
Какое-то время в начале 20 века то, что было сделано в математической логике, ещё не произвело никакого эффекта. Однако ситуация резко начала меняться с движением Бурбаки, которое начало разрастаться во Франции в примерное сороковые года.
Бурбаки придавали особое значение гораздо более абстрактному, логико-ориентированному подходу к математике. В частности, они акцентировали внимание на использовании обозначений там, где это только возможно, любым способом сводя использование потенциально неточного текста к минимуму.
Где-то с сороковых работы в области чистой математики претерпели серьёзные изменения, что можно заметить в соответствующих журналах, в работах международного математического сообщества и прочих источниках подобного рода. Изменения заключались в переходе от работ, полных текста и лишь с основными алгебраическими и вычислительными выкладками к работам, насыщенными обозначениями.
Конечно, эта тенденция коснулась не всех областей математики. Это в некотором роде то, чем занимаются в лингвистике обычных естественных языков. По устаревшим используемым математическим обозначениям можно заметить, как различные области, их использующие, отстают от основной магистрали математического развития. Так, к примеру, можно сказать, что физика осталась где-то в конце 19 века, используя уже устаревшую математическую нотацию тех времён.
Есть один момент, который постоянно проявляется в этой области — нотация, как и обычные языки, сильно разделяет людей. Я имею в виду, что между теми, кто понимает конкретные обозначения, и теми, кто не понимает, имеется большой барьер. Это кажется довольно мистическим, напоминая ситуацию с алхимиками и оккультистами — математическая нотация полна знаков и символов, которые люди в обычной жизни не используют, и большинство людей их не понимают.
На самом деле, довольно любопытно, что с недавних пор в рекламе появился тренд на использование математических обозначений. Думаю, по какой-то причине математическая нотация стала чем-то вроде шика. Вот один актуальный пример рекламы.
Отношение к математическим обозначениям, к примеру, в школьном образовании, часто напоминает мне отношение к символам секретных сообществ и тому подобному.
Что ж, это был краткий конспект некоторых наиболее важных эпизодов истории математической нотации.
В ходе исторических процессов некоторые обозначения перестали использоваться. Помимо некоторых областей, таких как математическая логика, она стала весьма стандартизированной. Разница в используемых разными людьми обозначениях минимальна. Как и в ситуации с любым обычным языком, математические записи практически всегда выглядят одинаково.
Вот вопрос: можно ли сделать так, чтобы компьютеры понимали эти обозначения?
Это зависит от того, насколько они систематизированы и как много смысла можно извлечь из некоторого заданного фрагмента математической записи.
Ну, надеюсь, мне удалось донести мысль о том, что нотация развивалась в результате непродуманных случайных исторических процессов. Было несколько людей, таких как Лейбниц и Пеано, которые пытались подойти к этому вопросу более системно. Но в основном обозначения появлялись по ходу решения каких-то конкретных задач — подобно тому, как это происходит в обычных разговорных языках.
И одна из вещей, которая меня удивила, заключается в том, что по сути никогда не проводилось интроспективного изучения структуры математической нотации.
Грамматика обычных разговорных языков развивалась веками. Без сомнения, многие римские и греческие философы и ораторы уделяли ей много внимания. И, по сути, уже примерно в 500 года до н. э. Панини удивительно подробно и ясно расписал грамматику для санскрита. Фактически, грамматика Панини была удивительно похожа по структуре на спецификацию правил создания компьютерных языков в форме Бэкуса-Наура, которая используется в настоящее время.
И были грамматики не только для языков — в последнее столетие появилось бесконечное количество научных работ по правильному использованию языка и тому подобному.
Но, несмотря на всю эту активность в отношении обычных языков, по сути, абсолютно ничего не было сделано для языка математики и математической нотации. Это действительно довольно странно.
Были даже математики, которые работали над грамматиками обычных языков. Ранним примером являлся Джон Уоллис, который придумал формулу произведения Уоллиса для числа пи, и вот он писал работы по грамматике английского языка в 1658 году. Уоллис был тем самым человеком, который начал всю эту суматоху с правильным использованием «will» или «shall«.
В начале 20 века в математической логике говорили о разных слоях правильно сформированного математического выражения: переменные внутри функций внутри предикатов внутри функций внутри соединительных слов внутри кванторов. Но не о том, что же это всё значило для обозначений выражений.
Некоторая определённость появилась в 50-е годы 20 века, когда Хомский и Бакус, независимо разработали идею контекстно-свободных языков. Идея пришла походу работы над правилами подстановки в математической логике, в основном благодаря Эмилю Посту в 20-х годах 20 века. Но, любопытно, что и у Хомского, и у Бакуса возникла одна и та же идея именно в 1950-е.
Бакус применил её к компьютерным языкам: сперва к Fortran, затем к ALGOL. И он заметил, что алгебраические выражения могут быть представлены в контекстно-свободной грамматике.
Хомский применил эту идею к обычному человеческому языку. И он отмечал, что с некоторой степенью точности обычные человеческие языки так же могут быть представлены контекстно-свободными грамматиками.
Конечно, лингвисты включая Хомского, потратили годы на демонстрацию того, насколько всё же эта идея не соответствует действительности. Но вещь, которую я всегда отмечал, а с научной точки зрения считал самой важной, состоит в том, что в первом приближении это всё-таки истина — то, что обычные естественные языки контекстно-свободны.
Итак, Хомский изучал обычный язык, а Бакус изучал такие вещи, как ALGOL. Однако никто из них не рассматривал вопрос разработки более продвинутой математики, чем простой алгебраический язык. И, насколько я могу судить, практически никто с тех времён не занимался этим вопросом.
Но, если вы хотите посмотреть, сможете ли вы интерпретировать некоторые математические обозначения, вы должны знать, грамматику какого типа они используют.
Сейчас я должен сказать вам, что считал математическую нотацию чем-то слишком случайным для того, чтобы её мог корректно интерпретировать компьютер. В начале девяностых мы горели идеей предоставить возможность Mathematica работать с математической нотацией. И по ходу реализации этой идеи нам пришлось разобраться с тем, что происходит с математической нотацией.
Нил Сойффер потратил множество лет, работая над редактированием и интерпретацией математической нотации, и когда он присоединился к нам в 1991, он пытаться убедить меня, что с математической нотацией вполне можно работать — как с вводом, так и с выводом.
Часть с выводом данных была довольно простой: в конце концов, TROFF и TEX уже проделали большую работу в этом направлении.
Вопрос заключался во вводе данных.
На самом деле, мы уже кое-что выяснили для себя касательно вывода. Мы поняли, что хотя бы на некотором уровне многие математические обозначения могут быть представлены в некоторой контекстно-свободной форме. Поскольку многие знают подобный принцип из, скажем, TEX, то можно было бы всё настроить через работу со вложенными структурами.
Но что насчёт входных данных? Один из самых важных моментов заключался в том, с чем всегда сталкиваются при парсинге: если у вас есть строка текста с операторами и операндами, то как задать, что и с чем группируется?
Итак, допустим, у вас есть подобное математическое выражение.2+ArcSin[x+1]+c(x+1)+f[x+1]
Что оно означает? Чтобы это понять, нужно знать приоритеты операторов — какие действуют сильнее, а какие слабее в отношении операндов.
Я подозревал, что для этого нет какого-то серьёзного обоснования ни в каких статьях, посвящённых математике. И я решил исследовать это. Я прошёлся по самой разнообразной математической литературе, показывал разным людям какие-то случайные фрагменты математической нотации и спрашивал у них, как бы они их интерпретировали. И я обнаружил весьма любопытную вещь: была удивительная слаженность мнений людей в определении приоритетов операторов. Таким образом, можно утверждать: имеется определённая последовательность приоритетов математических операторов.
Можно с некоторой уверенностью сказать, что люди представляют именно эту последовательность приоритетов, когда смотрят на фрагменты математической нотации.
Обнаружив этот факт, я стал значительно более оптимистично оценивать возможность интерпретации вводимых математических обозначений. Один из способов, с помощью которого всегда можно это реализовать — использовать шаблоны. То есть достаточно просто иметь шаблон для интеграла и заполнять ячейки подынтегрального выражения, переменной и так далее. И когда шаблон вставляется в документ, то всё выглядит как надо, однако всё ещё содержится информация о том, что это за шаблон, и программа понимает, как это интерпретировать. И многие программы действительно так и работают.
Но в целом это крайне неудобно. Потому что если вы попытаетесь быстро вводить данные или редактировать, вы будете обнаруживать, что компьютер вам бикает (beeping) и не даёт делать те вещи, которые, очевидно, должны быть вам доступны для реализации.
Дать людям возможность ввода в свободной форме — значительно более сложная задача. Но это то, что мы хотим реализовать.
Итак, что это влечёт?
Прежде всего, математический синтаксис должен быть тщательно продуманным и однозначным. Очевидно, получить подобный синтаксис можно, если использовать обычный язык программирования с основанным на строках синтаксисом. Но тогда вы не получите знакомую математическую нотацию.
Вот ключевая проблема: традиционная математическая нотация содержит неоднозначности. По крайней мере, если вы захотите представить её в достаточно общем виде. Возьмём, к примеру, «i«. Что это — Sqrt[-1] или переменная «i«?
В обычном текстовом InputForm в Mathematica все подобные неоднозначности решены простым путём: все встроенные объекты Mathematica начинаются с заглавной буквы.
Но заглавная «I» не очень то и похожа на то, чем обозначается Sqrt[-1] в математических текстах. И что с этим делать? И вот ключевая идея: можно сделать другой символ, который вроде тоже прописная «i», однако это будет не обычная прописная «i», а квадратный корень из -1.
Можно было бы подумать: Ну, а почему бы просто не использовать две «i», которые бы выглядели одинаково, — прям как в математических текстах — однако из них будет особой? Ну, это бы точно сбивало с толку. Вы должны будете знать, какую именно «i» вы печатаете, а если вы её куда-то передвинете или сделаете что-то подобное, то получится неразбериха.
Итак, значит, должно быть два «i«. Как должна выглядеть особая версия этого символа?
У нас была идея — использовать двойное начертание для символа. Мы перепробовали самые разные графические представления. Но идея с двойным начертанием оказалась лучшей. В некотором роде она отвечает традиции в математике обозначать специфичные объекты двойным начертанием.
Так, к примеру, прописная R могла бы быть переменной в математических записях. А вот R с двойным начертанием — уже специфический объект, которым обозначают множество действительных чисел.
Таким образом, «i» с двойным начертанием есть специфичный объект, который мы называем ImaginaryI. Вот как это работает:
Идея с двойным начертанием решает множество проблем.
В том числе и самую большую — интегралы. Допустим, вы пытаетесь разработать синтаксис для интегралов. Один из ключевых вопросов — что может означать «d» в интеграле? Что, если это параметр в подынтегральном выражении? Или переменная? Получается ужасная путаница.
Всё становится очень просто, если использовать DifferentialD или «d» с двойным начертанием. И получается хорошо определённый синтаксис.
Можно проинтегрировать x в степени d, деленное на квадратный корень от x+1. Вот как это работает:
Оказывается, что требуется всего лишь несколько маленьких изменений в основании математического обозначения, чтобы сделать его однозначным. Это удивительно. И весьма здорово. Потому что вы можете просто ввести что-то, состоящее из математических обозначений, в свободной форме, и оно будет прекрасно понято системой. И это то, что мы реализовали в Mathematica 3.
Конечно, чтобы всё работало так, как надо, нужно разобраться с некоторыми нюансами. К примеру, иметь возможность вводить что бы то ни было эффективным и легко запоминающимся путём., с помощью которой можно вводить явный верхний индекс. Та же идея для сочетания control — /, с помощью которого можно вводить «двухэтажную» дробь.
Наличие ясного набора принципов подобных этому важно для того, чтобы заставить всё вместе работать на практике. И оно работает. Вот как мог бы выглядеть ввод довольно сложного выражения:
Но мы можем брать фрагменты из этого результата и работать с ними.
И смысл в том, что это выражение полностью понятно для Mathematica, то есть оно может быть вычислено. Из этого следует, что результаты выполнения (Out) — объекты той же природы, что и входные данные (In), то есть их можно редактировать, использовать их части по отдельности, использовать их фрагменты в качестве входных данных и так далее.
Чтобы заставить всё это работать, нам пришлось обобщить обычные языки программирования и кое-что проанализировать. Прежде была внедрена возможность работать с целым «зоопарком» специальных символов в качестве операторов. Однако, вероятно, более важно то, что мы внедрили поддержку двумерных структур. Так, помимо префиксных операторов, имеется поддержка оверфиксных операторов и прочего.
Если вы посмотрите на это выражение, вы можете сказать, что оно не совсем похоже на традиционную математическую нотацию. Но оно очень близко. И оно несомненно содержит все особенности структуры и форм записи обычной математической нотации. И важная вещь заключается в том, что ни у кого, владеющим обычной математической нотацией, не возникнет трудностей в интерпретации этого выражения.
Конечно, есть некоторые косметические отличия от того, что можно было бы увидеть в обычном учебнике по математике. К примеру, как записываются тригонометрические функции, ну и тому подобное.
Однако я готов поспорить, что StandardForm в Mathematica лучше и яснее для представления этого выражения. И в книге, которую я писал много лет о научном проекте, которым я занимался, для представления чего бы то ни было я использовал только StandardForm.
Однако если нужно полное соответствие с обычными учебниками, то понадобится уже что-то другое. И вот другая важная идея, реализованная в Mathematica 3: разделить StandardForm и TraditionalForm.
Любое выражение я всегда могу сконвертировать в TraditionalForm.
И в действительности TraditionalForm всегда содержит достаточно информации, чтобы быть однозначно сконвертированным обратно в StandardForm.
Но TraditionalForm выглядит практически как обычные математические обозначения. Со всеми этими довольно странными вещами в традиционной математической нотации, как запись синус в квадрате x вместо синус x в квадрате и так далее.
Так что насчёт ввода TraditionalForm?
Вы могли заметить пунктир справа от ячейки [в других выводах ячейки были скрыты для упрощения картинок — прим. ред.]. Они означают, что есть какой-то опасный момент. Однако давайте попробуем кое-что отредактировать.
Мы прекрасно можем всё редактировать. Давайте посмотрим, что случится, если мы попытаемся это вычислить.
Вот, возникло предупреждение. В любом случае, всё равно продолжим.
Что ж, система поняла, что мы хотим.
Фактически, у нас есть несколько сотен эвристических правил интерпретации выражений в традиционной форме. И они работают весьма хорошо. Достаточно хорошо, чтобы пройти через большие объёмы устаревших математических обозначений, определённых, скажем, в TEX, и автоматически и однозначно сконвертировать их в осмысленные данные в Mathematica.
И эта возможность весьма вдохновляет. Потому что для того же устаревшего текста на естественном языке нет никакого способа сконвертировать его во что-то значимое. Однако в математике есть такая возможность.
Конечно, есть некоторые вещи, связанные с математикой, в основном на стороне выхода, с которыми существенно больше сложностей, чем с обычным текстом. Часть проблемы в том, что от математики часто ожидают автоматической работы. Нельзя автоматически сгенерировать много текста, который будет достаточно осмысленным. Однако в математике производятся вычисления, которые могут выдавать большие выражения.
Так что вам нужно придумывать, как разбивать выражение по строкам так, чтобы всё выглядело достаточно аккуратно, и в Mathematica мы хорошо поработали над этой задачей. И с ней связано несколько интересных вопросов, как, например, то, что во время редактирования выражения оптимальное разбиение на строки постоянно может меняться по ходу работы.
И это значит, что будут возникать такие противные моменты, как если вы печатаете, и вдруг курсор перескакивает назад. Что ж, эту проблему, полагаю, мы решили довольно изящным образом. Давайте рассмотрим пример.
Вы видели это? Была забавная анимация, которая появляется на мгновение, когда курсор должен передвинуться назад. Возможно, вы её заметили. Однако если бы вы печатали, вы бы, вероятно, и не заметили бы, что курсор передвинулся назад, хотя вы могли бы её и заметить, потому что эта анимация заставляет ваши глаза автоматически посмотреть на это место. С точки зрения физиологии, полагаю, это работает за счёт нервных импульсов, которые поступают не в зрительную кору, а прямо в мозговой ствол, который контролирует движения глаз. Итак, эта анимация заставляет вас подсознательно переместить свой взор в нужное место.
Таким образом, мы смогли найти способ интерпретировать стандартную математическую нотацию. Означает ли это, что теперь вся работа в Mathematica должна теперь проводиться в рамках традиционных математических обозначений? Должны ли мы ввести специальные символы для всех представленных операций в Mathematica? Таким образом можно получить весьма компактную нотацию. Но насколько это разумно? Будет ли это читаемо?
Пожалуй, ответом будет нет.
Думаю, тут сокрыт фундаментальный принцип: кто-то хочет всё представлять в обозначениях, и не использовать ничего другого.
А кому-то не нужны специальные обозначения. А кто-то пользуется в Mathematica FullForm. Однако с этой формой весьма утомительно работать. Возможно, именно поэтому синтаксис языков наподобие LISP кажется столь трудным — по сути это синтаксис FullForm в Mathematica.
Другая возможность заключается в том, что всему можно присвоить специальные обозначения. Получится что-то наподобие APL или каких-то фрагментов математической логики. Вот пример этого.
Довольно трудно читать.
Вот другой пример из оригинальной статьи Тьюринга, в которой содержатся обозначения для универсальной машины Тьюринга, опять-таки — пример не самой лучшей нотации.
Она тоже относительно нечитабельная.
Вопрос заключается в том, что же находится между двумя такими крайностями, как LISP и APL. Думаю, эта проблема очень близка к той, что возникала при использовании очень коротких имён для команд.
К примеру, Unix. Ранние версии Unix весьма здорово смотрелись, когда там было небольшое количество коротких для набора команд. Но система разрасталась. И через какое-то время было уже большое количество команд, состоящих из небольшого количества символов. И большинство простых смертных не смогли бы их запомнить. И всё стало выглядеть совершенно непонятным.
Та же ситуация, что и с математической или другой нотацией, если на то пошло. Люди могут работать лишь с небольшим количеством специальных форм и символов. Возможно, с несколькими десятками. Соизмеримым с длиной алфавита. Но не более. А если дать им больше, особенно все и сразу, в голове у них будет полная неразбериха.
Это следует немного конкретизировать. Вот, к примеру, множество различных операторов отношений.
Но большинство из них по сути состоят из небольшого количества элементов, так что с ними проблем быть не должно.
Конечно, принципиально люди могут выучить очень большое количество символов. Потому что в языках наподобие китайского или японского имеются тысячи иероглифов. Однако людям требуется несколько дополнительных лет для обучения чтению на этих языках в сравнении с теми, которые используют обычный алфавит.
Если говорить о символах, кстати, полагаю, что людям гораздо легче справится с какими-то новыми символами в качестве переменных, нежели в качестве операторов. И весьма занятно рассмотреть этот вопрос с точки зрения истории.
Один из наиболее любопытных моментов — во все времена и практически без исключения в качестве переменных использовались лишь латинские и греческие символы. Ну, Кантор ввёл алеф, взятый из иврита, для своих кардинальных чисел бесконечных множеств. И некоторые люди утверждают, что символ частной производной — русская д, хотя я думаю, что на самом деле это не так. Однако нет никаких других символов, которые были бы заимствованы из других языков и получили бы распространение.
Кстати, наверняка вам известно, что в английском языке буква «e» — самая популярная, затем идёт «t«, ну и так далее. И мне стало любопытно, каково распределение по частоте использования букв в математике. Потому я исследовал сайт MathWorld, в котором содержится большое количество математической информации — более 13 500 записей, и посмотрел, каково распределение для различных букв [к сожалению, эту картинку, сделанную Стивеном, не удалось осовременить — прим. ред.].
Можно увидеть, что «e» — самая популярная. И весьма странно, что «a» занимает второе место. Это очень необычно. Можно увидеть, что строчная π — наиболее популярная, за которой идут θ, α, φ, μ, β и так далее. А среди прописных самые популярные — Γ и Δ.
Хорошо. Я немного рассказал об обозначениях, которые в принципе можно использовать в математике. Так какая нотация лучше всего подходит для использования?
Большинство людей, использующих математическую нотацию, наверняка задавались этим вопросом. Однако для математики нет никакого аналога, подобного «Современному использованию английского языка» Фаулера для английского языка. Была небольшая книжка под названием Математика в печати, изданная AMS, однако она в основном о типографских приёмах.
В результате мы не имеем хорошо расписанных принципов, аналогичным вещам наподобие инфинитивов с отдельными частицами в английском языке.
Если вы используете StandardForm в Mathematica, вам это больше не потребуется. Потому что всё, что вы введёте, будет однозначно интерпретировано. Однако для TraditionalForm следует придерживаться некоторых принципов. К примеру, не писать , потому что не совсем ясно, что это означает.
Чтобы закончить, позвольте мне рассказать немного о будущем математической нотации.
Какой, к примеру, должна бы быть новая нотация?
В какой-нибудь книге символов будет содержаться около 2500 символов, популярных в тех или иных областях и не являющимися буквами языков. И с правильным написанием символов, многие из них могли бы идеально сочетаться с математическими символами.
Для чего же их использовать?
Первая приходящая на ум возможность — нотация для представления программ и математических операций. В Mathematica, к примеру, представлено довольно много текстовых операторов, используемых в программах. И я долгое время считал, что было бы здорово иметь возможность использовать для них какие-то специальные символы вместо комбинаций обычных символов ASCII [последние версии Mathematica полностью поддерживают Unicode — прим. ред.].
Оказывается, иногда это можно реализовать весьма просто. Поскольку мы выбрали символы ASCII, то часто можно получить некоторые символы, очень близкие по написанию, но более изящные. К примеру, если в Mathematica набрать ->, то эта стрелочка автоматически превратиться в более изящную . И это всё реализуемо за счёт того, что парсер в Mathematica может работать в том числе и со специальными символами.
Я часто размышлял о том, как бы расширить всё это. И вот, постепенно появляются новые идеи. Обратите внимание на знак решётки #, или номерной знак, или, как его ещё иногда называют, октоторп, который мы используем в тех местах, в которые передаётся параметр чистой функции. Он напоминает квадрат с щупальцами. И в будущем, возможно, он будет обозначаться симпатичным квадратиком с маленькими засечками, и будет означать место для передачи параметра в функцию. И он будет более гладким, не похожим на фрагмент обычного кода, чем-то вроде пиктограммы.
Насколько далеко можно зайти в этом направлении — представлении вещей в визуальной форме или в виде пиктограмм? Ясно, что такие вещи, как блок-схемы в инженерии, коммутативные диаграммы в чистой математике, технологические схемы — все хорошо справляются со своими задачами. По крайней мере до настоящего момента. Но как долго это может продолжаться?
Не думаю, что уж очень долго. Думаю, некоторые приближаются к некоторым фундаментальным ограничениям людей в обработке лингвистической информации.
Когда языки более или менее контекстно-свободные, имеют древовидную структуру, с ними можно многое сделать. Наша буферная память из пяти элементов памяти и что бы то ни было спокойно сможет их разобрать. Конечно, если у нас будет слишком много вспомогательных предложений даже на контекстно-свободном языке, то будет вероятность исчерпать стековое пространство и попасть впросак. Но, если стек не будет заходить слишком глубоко, то всё будет работать как надо.
Но что насчёт сетей? Можем ли мы понимать произвольные сети? Я имею в виду — почему у нас должны быть только префиксные, инфиксные, оверфиксные операторы? Почему бы операторам не получать свои аргументы через какие-то связи внутри сети?
Меня особенно интересовал этот вопрос в контексте того, что я занимался некоторыми научными вопросами касательно сетей. И мне действительно хотелось бы получить некоторое языковое представление для сетей. Но не смотря на то, что я уделил этому вопросу довольно много времени — не думаю, что мой мозг смог бы работать с подобными сетями так же, как с обычными языковыми или математическими конструкциями, имеющими одномерную или двумерную контекстно-свободную структуру. Так что я думаю, что это, возможно, то место, до которого нотация не сможет добраться.
Вообще, как я упоминал выше, это частый случай, когда язык или нотация ограничивают наше пространство мыслимого.
Итак, что это значит для математики?
В своём научном проекте я разрабатывал некоторые основные обобщения того, что люди обычно относят к математике. И вопрос в том, какие обозначения могут быть использованы для абстрактного представления подобных вещей.
Что ж, я не смог пока что полностью ответить на этот вопрос. Однако я обнаружил, что, по крайней мере в большинстве случаев, графическое представление или представление в виде пиктограмм гораздо эффективнее обозначений в виде конструкций на обычных языках.
Возвращаясь к самому началу этого разговора, ситуация напоминает то, что происходило тысячи лет в геометрии. В геометрии мы знаем, как представить что-то в графическом виде. Ещё со времён древнего Вавилона. И чуть более ста лет назад стало ясно, как можно формулировать геометрические задачи с точки зрения алгебры.
Однако мы всё ещё не знаем простого и ясного способа представлять геометрические схемы в обозначениях на естественном языке. И моя догадка состоит в том, что практически все эти математические вещи лишь в небольшом количестве могут быть представлены в обозначениях на естественном языке.
Однако мы — люди — легко воспринимаем лишь эти обозначения на естественном языке. Так что мы склонны изучать те вещи, которые могут быть представлены этим способом. Конечно, подобные вещи не могут быть тем, что происходит в природе и вселенной.
Но это уже совсем другая история. Так что я лучше закончу на этом.
Большое спасибо.
В ходе обсуждения после выступления и во время общения с другими людьми на конференции возникло несколько моментов, которые следовало бы обсудить.
Эмпирические законы для математических обозначений
При изучении обычного естественного языка были обнаружены различные историко-эмпирические законы. Пример — Закон Гримма, которые описывает переносы в согласных на индоевропейских языках. Мне было любопытно, можно ли найти подобные историко-эмпирические законы для математического обозначения.
Дана Скотт предложила такой вариант: тенденция к удалению явных параметров.
Как пример, в 60 годах 19 века часто каждый компонент вектора именовался отдельно. Но затем компоненты стали помечать индексами — как ai. И вскоре после этого — в основном после работ Гиббса — векторы стали представлять как один объект, обозначаемый, скажем, как или a.
С тензорами всё не так просто. Нотацию, избегающую явных индексов, обычно называют координатно-свободной. И подобная нотация — частое явление в чистой математике. Однако в физике данный подход считается слишком абстрактным, потому явные индексы используются повсеместно.
В отношении функций так же имеется тенденция явно не упоминать параметры. В чистой математике, когда функции рассматриваются через сопоставления, они часто упоминаются лишь по своему имени — просто f, без каких-либо параметров.
Однако это будет хорошо только тогда, когда у функции только один параметр. Когда параметров несколько, обычно становится непонятно, как будут работать те потоки данных, которые ассоциированы с параметрами.
Однако, ещё в 20-х годах 20 века было показано, что можно использовать так называемые комбинаторы для определения подобных потоков данных без какого-либо явного указания параметров.
Комбинаторы не использовались в основных течениях математики, однако время от времени становились популярными в теории вычислений, хотя их популярность заметно поубавилась из-за несовместимости с идеей о типах данных.
Комбинаторы довольно легко задать в Mathematica через задание функции с составным заголовком. Вот как можно определить стандартные комбинаторы:
k[x_][y_]:=i x
s[x_][y_][z_]:= x[z][y[z]]
Если определить целое число n, по сути, в унарной системе, используя Nest[s[s[k[s]][k]],k[s[k][k]],n], то тогда сложение можно будет определить как s[k[s]][s[k[s[k[s]]]][s[k[k]]]], умножение как s[k[s]][k], а степень — s[k[s[s[k][k]]]][k]. Никакие переменные не требуются.
Проблема заключается в том, что выражения получаются непонятными, и с этим ничего не поделать. Я пытался найти какие-то способы для более ясного представления их и сопряжённых с ними вычислений. Я добился небольшого прогресса, однако нельзя сказать, что задача была решена.
Печатные обозначения против экранных
Некоторые спрашивали о разнице в возможностях печатных и экранных обозначений.
Чтобы можно было понимать обозначения, они должны быть похожими, и разница между ними не должна быть очень большой.
Но есть некоторые очевидные возможности.
Во-первых, на экране легко можно использовать цвет. Можно было бы подумать, что было каким-то образом удобно использовать разные цвета для переменных. Мой опыт говорит о том, что это удобно для разъяснения формулы. Однако всё станет весьма запутанным, если, к примеру, красному x и зелёному x будут соответствовать разные переменные.
Другая возможность состоит в том, чтобы иметь в формуле какие-то анимированные элементы. Полагаю, что они будут столь же раздражающими, как и мигающий текст, и не будут особо полезными.
Пожалуй, идея получше — иметь возможность скрывать и разворачивать определённые части выражения — как группы ячеек в ноутбуке Mathematica. Тогда будет возможность сразу получить представление обо всём выражении, а если интересны детали, то разворачивать его далее и далее.
Письменные обозначения
Некоторые могли бы подумать, что я уж слишком много времени уделил графическим обозначениям.
Хотелось бы прояснить, что я нахожу довольно затруднительным графические обозначения обычных математических действий и операций. В своей книге A New Kind of Science я повсеместно использую графику, и мне не представляется никакого другого способа делать то, что я делаю.
И в традиционной науке, и в математике есть множество графических обозначений, которые прекрасно работают, пускай и в основном для статичных конструкций.
Теория графов — очевидный пример использования графического представления.
К ним близки структурные диаграммы из химии и диаграммы Фейнмана из физики.
В математике имеются методы для групповых теоретических вычислений, представленные отчасти благодаря Предрагу Цвитановицу, и вот они основаны на графическом обозначении.
И в лингвистике, к примеру, распространены диаграммы для предложений, показывающие дерево лингвистических компонентов и способы их группировки для образования предложения.
Все эти обозначения, однако, становятся малопригодными в случаях исследования каких-то очень крупных объектов. Однако в диаграммах Фейнмана обычно используется две петли, а пять петель — максимум, для которого когда-либо были сделаны явные общие вычисления.
Шрифты и символы
Я обещал рассказать кое-что о символах и шрифтах.
В Mathematica 3 нам пришлось проделать большую работу чтобы разработать шрифты для более чем 1100 символов, имеющих отношение к математической и технической нотации.
Получение правильной формы — даже для греческих букв — часто было достаточно сложным. С одной стороны, мы хотели сохранить некоторую традиционность в написании, а с другой — сделать греческие буквы максимально непохожими на английские и какие бы то ни было другие.
В конце концов я сделал эскизы для большинства символов. Вот к чему мы пришли для греческих букв. Мы разработали Times-подобный шрифт, моноширинный наподобие Courier, а сейчас разрабатываем sans serif. Разработать шрифт Courier было непростой задачей. Нужно, к примеру, было придумать, как сделать так, чтобы йота занимала весь слот под символ.
Так же сложности были со скриптовыми и готическими (фактурными) шрифтами. Часто в этих шрифтах буквы настолько непохожи на обычные английские, что становятся абсолютно нечитаемыми. Мы хотели, чтобы эти шрифты вписывались в соответствующую им тему, и, тем не менее, обладали бы теми же габаритами, что и обычные английские буквы.
Вот, что у нас получилось:
Веб сайт fonts.wolfram.com, в котором собрана вся детальная информация о символах и шрифтах, разумеется, если они имеют отношение к Mathematica и её шрифтам.
Поиск математических формул
Некоторые люди спрашивали о поиске математических формул [после создания Wolfram|Alpha появился гигантский объем баз данных, доступных в языке Wolfram Language, теперь можно получить огромный массив информации о любых формулах с помощью функции MathematicalFunctionData — прим. ред.].
Очевидно легко сказать, что же такое поиск обычного текста. Единственная вопрос заключается в эквивалентности строчных и прописных букв.
Для математических формул всё сложнее, потому что есть ещё много различных эквивалентностей. Если спрашивать о всех возможных эквивалентностях, то всё станет слишком сложным. Но, если спросить об эквивалентностях, которые просто подразумевают замену одной переменной другой, то всегда можно определить, эквивалентны ли два выражения.
Однако, для этого потребуется мощь обнаружителя одинаковых паттернов Mathematica.
Мы планируем встроить возможности по поиску формул в наш сайт functions.wolfram.com, однако тут я не буду останавливаться на подробностях.
Невизуальные обозначения
Кто-то спрашивал о невизуальных обозначениях.
Первая мысль, которая у меня возникла, заключалась в том, что человеческое зрение даёт гораздо больше информации, чем, скажем, слух. В конце концов, с нашими глазами соединён миллион нервных окончаний, а с ушами лишь 50 000.
В Mathematica встроены возможности по генерации звуков начиная со второй версии, которая была выпущена в 1991 году. И были некоторые моменты, когда эта функция оказывалась полезной для понимания каких-то данных.
Однако я никогда не находил подобную функцию полезной для чего-то, связанного с обозначениями.
Доказательства
Кто-то спрашивал о представлении доказательств.
Самая большая проблема заключается в представлении длинных доказательств, которые были автоматически найдены с помощью компьютера.
Большое количество работы было проделано для представления доказательств в Mathematica. Примером является проект Theorema.
Самые сложные для представления доказательства — скажем, в логике — представляют из себя некоторую последовательность преобразований. Вот пример такого доказательства:
Даны аксиомы Шеффера для логики (f это NAND):
{f[f[a,a],f[a,a]]==a,f[a,f[b,f[b,b]]]==f[a,a], f[f[a,f[b,c]],f[a,f[b,c]]]==f[f[f[b,b],a],f[f[c,c],a]]}
Доказать коммутативность, то есть что f[a,b]==f[b,a]:
Замечание (a b) есть Nand[a,b]. В этом доказательстве L == лемма, A == аксиома, и T == теорема.
Отбор символов
Я хотел бы кое-что рассказать о выборе символов для использования в математической нотации.
Существует около 2500 часто используемых символов, которые не встречаются в обычном тексте.
Некоторые из них слишком картинны — скажем, обозначение для хрупких предметов. Некоторые слишком витиеватые. Некоторые полны чёрной заливки, так что они будут слишком сильно выделяться на странице (символ радиации, например).
Но некоторые могут быть вполне приемлемыми.
Если заглянуть в историю, часто можно наблюдать картину, как со временем написание некоторых символов упрощается.
Особой проблемой, с которой я не так давно столкнулся, был выбор хорошего обозначения для таких логических операций, как NAND, NOR, XOR.
В литературе по логике NAND обозначается по-разному:
Ни одно из этих обозначений мне особо не нравилось. В основном они наполнены тонкими линиями и недостаточно цельны для того, чтобы представлять бинарные операторы. Однако они передают своё содержание.
Я пришёл к следующему обозначению для оператора NAND, который основан на стандартном, однако имеющим улучшенную визуальную форму. Вот текущая версия того, к чему я пришёл:
Частотное распределение символов
Я упоминал о частотном распределении греческих букв в MathWorld.
В дополнение к этому я также посчитал количество различных объектов, именуемых с помощью букв, которые появляются в словаре физических терминов и математических сокращений. Вот результаты.
В более ранних образцах математической нотации, скажем, в 17 веке, обычные слова шли вперемешку с различными символами.
Однако всё более в таких сферах, как математика и физика, проявлялась тенденция к исключению слов из обозначений и именования переменных одной или двумя буквами.
В некоторых областях инженерии и социальных наук, куда математика дошла не так давно и не является слишком абстрактной, обычные слова гораздо чаще можно встретить в качестве имён переменных.
Та же история с современными тенденциями в программировании. И всё работает хорошо, пока формулы достаточно просты. Однако по мере усложнения формул нарушается их визуальный баланс, и становится уже сложно разглядеть их общую структуру.
Части речи в математической нотации
В разговоре о соответствии языка математики и обычного языка я хотел упомянуть вопрос частей речи.
Насколько я знаю, во всех обычных языках есть глаголы и существительные, и в большинстве из них есть прилагательные, наречия и др.
В математической нотации можно представлять переменные как существительные и глаголы как операторы.
А что насчёт других частей речи?
Вещи наподобие иногда играют роль союзов, как и в обычных языках (примечательно, что во всех языках есть отдельные слова для AND и OR, однако ни в одном нет слова для NAND). А в качестве префиксного оператора может рассматриваться как прилагательное.
Однако не до конца ясно, в какой мере различные виды лингвистических структур, связанные с частями речи на обычном языке, отражены в математическом обозначении.
По вопросам о технологиях Wolfram пишите на [email protected]
Обозначение— Использование знака приближения
Вы можете связать любые бинарные отношения.
Например,
$$
a \ leq b = c Из приведенной выше цепочки вы можете, например, сделать вывод, что $ a Другой пример:
$$
г = ч \ примерно я = J = к \ примерно л
$$
действительно означает, что $ g \ приблизительно l $. Я бы сказал, что два приближения все еще нормально.
Отношение «$ \ приблизительно $» не определено строго, и как вопрос, так и этот ответ выходят за рамки полностью строгой математики.
Он определяется эвристически (мы вроде как знаем, что это означает), и у этого эвристического значения есть свойства.Одно из проблемных свойств — транзитивность.
Если растянуть слишком далеко, это становится смешным: $ 1.00 \ приблизительно1.01 \ приблизительно1.02 \ приблизительно \ cdots \ приблизительно1.99 \ приблизительно2.00 $ и так $ 1 \ приблизительно2 $, а по индукции $ n \ приблизительно m $ для любых двух целые числа $ n, m $.
Однако я не вижу проблемы в практических расчетах, как в вопросе, и я бы с уверенностью заключил, что $ g \ приблизительно l $ в моем втором примере.
Приближение потенциально ухудшается при повторении, но всего пара шагов не является большой проблемой в этом контексте. Важно четко и постоянно говорить вашим ученикам, что
$$
129.87 \ cdot 6 \ приблизительно 130 \ cdot 6 = 780
$$
означает два оператора в одном: $ 129.87 \ cdot 6 \ приблизительно 130 \ cdot 6 $ и $ 130 \ cdot 6 = 780 $.
Мой опыт подсказывает, что не все студенты поймут это, если (даже если?) Не расскажут.
Из этих двух утверждений следует, что $ 129.87 \ cdot 6 \ Approx780 $, но это не указано прямо . Я бы посоветовал ваш первый вариант.
Но и второй вариант на самом деле не ошибочен; и $ 130 \ cdot 6 = 780 $ и $ 130 \ cdot 6 \ приблизительно 780 $ верны.
Но может сбивать с толку использование «$ \ приблизительно $», когда эти две вещи фактически равны. Этот текст можно прочитать вслух как « примерно равно » или « примерно равно ». Примеры: — Предпочтительный способ обозначения «приблизительно равно» — использовать символ ≈, символ ~ или (в некоторых случаях) символ ≅ (см. Примечание 2). Однако : «= ~» — это простая в использовании и легко запоминающаяся альтернатива. « ~ = » — это логически возможное расширение, которое многие люди интерпретируют как «приблизительно равно» (а не как использование «конгрунета» в геометрии). Если текст можно ввести как HTML, вы также можете использовать следующие обозначения: 49 2266 49 2266 ≦ При сравнении величин значения могут быть почти равными, но не в точности равными или идентичными. Так как было бы ошибочно показывать сравнение с параллельными линиями знака равенства, символ печати для приблизительно равных состоит из параллельных волнистых линий, двойной тильды. Брайлевский символ приблизительно равен, точка четыре точки один пять шесть точек четыре точки один пять шесть, напоминает его печатный эквивалент. Он использует символ тильды, но в вертикальной, а не горизонтальной конфигурации. ≈ примерно равно Если размеры соответствующих углов равны, а размеры соответствующих сторон равны, геометрические фигуры считаются математически подобными. Символ печати для подобия состоит из одной волнистой линии, тильды. Брайлевский символ для подобного - это точка четыре точки один пять шесть. ∼ аналогично Если две фигуры подобны и размеры их сторон равны, то фигуры считаются конгруэнтными.И печатные символы, и символы Брайля сочетают в себе символ сходства с символом равенства. В печатном виде тильда появляется над знаком равенства. Знак Брайля для конгруэнтности - это точка четыре точки один пять шесть точек четыре шесть точек один три. ≅ соответствует 1,78≈1,8 π≈3,14 & xutri; ABC∼ & xutri; XYZ трапецияABCD∼ трапеция MNOP & xutri; ABC≅ & xutri; XYZ AB и OverBar; &CD и OverBar; ∠A≅∠B предыдущая - следующая (упражнения) Примечание: доступность веб-сайтов APH Следующий список содержит некоторые из наиболее известных символов в математике.Обратите внимание, что эти символы могут иметь разные значения в разных контекстах. = ≡ ≈ ≠ < > ≪ ≫ ≤ неравенство ≥ ∝ + – × · ÷ / ± ∓ √ ∑ ∏ ! ⇒ ⇔ |… | || ⊥ ≅ φ ∞ ∈ ∉ {,} ℕ ℤ ℚ ℝ ℂ х х В этом разделе собраны математические символы, которые нельзя правильно ввести с клавиатуры. Представленный набор можно разделить на несколько групп: Парабола: ƒ (x) = ax² + bx + c (a ≠ 0) Представление исключительного ИЛИ: A⊕B: ⇔ (A⋁B) ∧¬ (A∧B) Скорость тела, падающего с высоты h: V = √̅2̅g̅h̅ Использование этих значков - единственный способ вставить различные математические символы на веб-сайт или в сообщение, появляющееся в любой операционной системе. Надо просто скопировать кодовый знак. Использование изображений для таких целей усложняет процесс: они требуют настройки при разработке или наполнении Интернет-сайта.Кроме того, мультимедийный контент занимает слишком много места на диске. Математические знаки можно использовать в социальных сетях, чатах и форумах. Они также могут быть полезны веб-разработчикам. Математика как язык всех наук не может существовать без системы письма. Его многочисленные концепции и операторы приобрели свои шрифты по мере развития науки. Поскольку стандартные алфавиты не включают их, набрать эти символы довольно проблематично. Вы можете легко скопировать их на нашем сайте и вставить. Unicode включил в себя множество различных знаков. Если вы не можете найти то, что вам нужно, попробуйте поискать по сайту или просмотрите следующие разделы: Математические операторы 2200–22FF Разные математические символы-A 27C0–27EF Разные математические символы-B 2980–29FF Дополнительные математические операторы 2A00–2AFF Буквы для формул: Греческий и коптский 0370–03FF Математические буквенно-цифровые символы 1D400–1D7FF Мы сделали еще один набор для надстрочных и подстрочных чисел. Исчерпывающий список математических символов и их значения [+ Загружаемая таблица для класса]
{} набор набор элементов A = {3,7,9,14},
B = {9,14,28} | так, что так, чтобы A = { x | x ∈, x <0} A⋂B пересечение объектов, принадлежащих набору A и набору B A ⋂ B = {9,14} A⋃B union объектов, которые принадлежат набору A или набору B A ⋃ B = {3,7,9,14,28} A⊆B подмножество A является подмножеством B.набор A включен в набор B. {9,14,28} ⊆ {9,14,28} A⊂B собственное подмножество / строгое подмножество A является подмножеством B, но A не равно B. {9,14} ⊂ {9,14,28} A⊄B не подмножество набор A не является подмножеством набора B {9,66} ⊄ {9,14,28} A⊇B расширенный набор A является расширенным набором B. набор A включает набор B {9,14,28} ⊇ {9,14,28} A⊃B правильный суперсет / строгий суперсет A — надмножество B, но B не равно A. {9,14,28} ⊃ {9,14} A⊅B не расширенный набор A не является расширенным набором B {9,14,28} ⊅ {9, 66} 2 A набор мощности все подмножества A нет данных power set все подмножества A нет A = B равенство оба набора имеют одинаковые элементы A = {3,9,14},
B = {3,9,14},
A = B A c дополнить все объекты, которые не принадлежат набору A н / д A ‘ дополнить все объекты, которые не принадлежат установить A n / a A \ B относительное дополнение объектов, которые принадлежат A, а не B A = {3,9,14},
B = {1,2,3},
A \ B = {9,14} A-B относительное дополнение объектов, которые принадлежат A, а не B A = {3,9,14},
B = {1,2,3},
A — B = {9,14} A∆B симметричная разность объектов, принадлежащих A или B, но не их пересечению A = {3,9,14},
B = {1,2,3},
A ∆ B = {1,2,9,14} A⊖B симметричная разность объектов, принадлежащих A или B, но не их пересечению A = {3,9,14},
B = {1,2,3},
A ⊖ B = {1,2,9,14} a ∈A элемент,
принадлежит установленному членству A = {3,9,14}, 3 ∈ A x ∉A не элемент нет установленного членства A = {3,9,14 }, 1 ∉ A ( a , b ) заказанная пара набор из 2 элементов н / д A × B декартово произведение набор всего заказанного пары из A и B н / д | A | мощность количество элементов набора A A = {3,9,14}, | A | = 3 #A мощность количество элементов набора A A = {3,9,14}, # A = 3 aleph-null бесконечная мощность множества натуральных чисел нет данных aleph-one мощность счетного ординала набор номеров нет данных Ø пустой набор Ø = {} A = Ø универсальный набор набор всех возможных значений нет 0 набор натуральных / целых чисел (с нулем) 0 = {0,1,2,3,4 ,…} 0 ∈ 0 1 натуральные числа / набор целых чисел (без нуля) 1 = {1,2,3,4,5, …} 6 ∈ 1 набор целых чисел = {…- 3, -2, -1,0,1,2,3, …} -6 ∈ набор рациональных чисел = { x | x = a / b , a , b ∈ и b ≠ 0} 2/6 ∈ набор вещественных чисел = { x | -∞ < x <∞} 6.343434 ∈ набор комплексных чисел = { z | z = a + bi , -∞ < a <∞, -∞ < b <∞} 6 + 2 i ∈ равно приблизительно (= ~)
Способ написания «приблизительно равно» («почти равно» \ «приблизительно равно» \ «приблизительно равно») в стандартном тексте в Интернете * или в текстовых приложениях:
«Один мегабайт … равен восьми миллионам триста восемьдесят восемь тысяч шестисот восьми битам, (что) приблизительно равно одному миллиону байтов.»
» Один мегабайт … равен восьми миллионам триста восемьдесят восемь тысяч шестьсот восемь бит, (что) приблизительно равно одному миллиону байтов «.
«Один гигабайт примерно равен одному миллиарду байтов …».
«Один гигабайт равен примерно одному миллиарду байтов ….»
* электронная почта, формы комментариев, форумы, доски объявлений и т. 2 = 50 (это должен быть символ» приблизительно равно «, но мне лень придумать, как получить один из них)… «
• ≅ и ≈ — символы, которые нелегко ввести в электронную почту, форумы и т. Д. (нет стандартизированного метода ввода с клавиатуры).
• ≅ и ≈ — символы, которые не всегда корректно отображаются в веб-браузерах (на самом деле, вы можете видеть прямоугольники вместо символов прямо сейчас ) и обычно неправильно анализируются в веб-инструментах, таких как комментарии и форумы.
• символ ~ слишком часто используется для обозначения другого значения (например, «НЕ») или для украшения.
(
Примечание. В HTML 4 «~» определяется как «изменяется с» или «похоже на».) Почему не ~ =?
Кроме того, « ~ = » можно читать как «приблизительно равно». Однако в некоторых языках программирования « ~ » является символом НЕ (побитовое), и поэтому « ~ = » иногда используется как вариант «! = », что означает НЕ РАВНО.
Из-за этого потенциального источника путаницы вместо этого предлагается «= ~». Предпочтительные символы
Примечание 1:
«асимптотика к, U + 2248» означает, точнее, « почти равно»; часто, если приближение более широкое \ менее точное, предпочтительнее ~.
Примечание 2:
≅ (& # 8773; ‘U + 2245’) определяется в HTML 4 как « cong »: «конгруэнтно» — имеет точно или почти такой же размер и форму, имеет соответствие; с такими же характеристиками нет
Разные математические символы
2200 ∀ Для всех = универсальный квантификатор Дополнение 2201 → 0297 растянутая латинская буква c 2202 ∂ Частичный дифференциал 2203 ∃ Есть Exists = квантификатор существования 2204 ∄ Не существует ≡ 2203 ∃ 1 2205 ∅ Пустой набор = Пустой набор • используется в лингвистике для обозначения нулевой морфемы или фонологического «нуля» → 00D8 Ø заглавная латинская буква o с ходом → 2300 Знак диаметра 2206 ∆ Шаг = Оператор Лапласа = разность вперед = симметричная разность (в теории множеств) • другие символы также могут использоваться для симметричных d ifference → 0394 Δ дельта греческой заглавной буквы → 25B3 △ белый треугольник, указывающий вверх 2207 Nabla = разница в обратном направлении = градиент, del • используется для оператора лапласа (пишется с надстрочным индексом 2 ) → 25BD ▽ белый треугольник, направленный вниз Установить членство
2208 ∈ Элемент 220 ∉ Не элемент 90 021 ≡ 2208 ∈ 0338 ◌̸ 220A ∊ Малый элемент в math. шрифты; не прямой эпсилон → 03F5 ϵ греческий полулунный символ эпсилон 220B ∋ Содержит как член = такой что 220C ∌ Не содержит в качестве элемента ≡ 220B ∋ 0338 ◌̸ 220D Маленький содержит как элемент → 03F6 ϶ греческий обратный полулунный символ эпсилон Прочие математические символы
220E ∎ 1 Конец = кв.e.d. → 2023 ‣ треугольная пуля → 25AE ▮ черный вертикальный прямоугольник N-арные операторы
21 ∏ N-Ary Продукт = знак продукта → 03A0 Π греческая заглавная буква pi 2210 ∐ N-Ary Coproduct = знак сопродукта 2211 ∑ N-Ary Summing суммирование знак → 03A3 Σ греческая заглавная буква сигма → 2140 ⅀ двойное начертание n-арное суммирование Операторы
Знак минус 221220 --550 → 002D - дефис-минус → 2796 ➖ жирный знак минус 2213 ∓ Знак минус-или-плюс → 00B1 ± знак плюс-минус 2214 ∔ Точка Плюс 2215 ∕ Division Slash • общее деление n оператор → 002F / солидус → 2044 ⁄ дробная косая черта → 27CB математическая восходящая диагональ 2216 ∖ Установить Минус → 005C \ обратный солидус → 27CD падающая диагональ → 29F5 ⧵ оператор обратного солидуса 2217 ∗ Asterisk Operator → 002A 2218 ∘ Кольцевой оператор = составная функция = APL jot → 00B Знак ° градус → 0970 ॰ знак аббревиатуры деванагари → 25E6 ◦ белая пуля → 900 10B39 𐬹 аббревиатура авестийской марки 2219 ∙ Bullet Operator → 00B7 · средняя точка • пуля → 2024 ․ выноска с одной точкой 221A √ Квадратный корень = радикальный знак → 2713 ✓ галочка 221B ∛ Корень куба → 0606 ؆ арабско-индийский корень куба 221C 1 900 Четвертый → 0607 ؇ арабско-индийский корень четвертой степени 221D ∝ Пропорционально → 03B1 α21 греческая строчная буква Прочие математические символы
221E ∞ Infinity Углы
221F ∟ Прямой угол → 2BFE ⯾ перевернутый прямой угол 2220 ∠ Угол • квадрат используется в астрологических контекстах 21 для → 299F ⦟ острый угол 2221 ∡ Измеренный угол 2222 ∢ 1 = угол дуги Взаимосвязи
2223 ∣ Делит = таким образом, что = → 007C | вертикальная линия → 01C0 ǀ латинские буквы стоматологический щелчок 2224 ∤ Не разделяет ≡ 22 ∣ 0338 ◌̸ 2225 ∥ Параллельно → 01C1 ǁ латинские буквы боковой щелчок 2016 ‖ двойная вертикальная линия 2226 ∦ Не параллельно ≡ 2225 ∥ 0338 ◌̸ Логический и набор операторы 2227 ∧ 9 0021 Логическое И = клин, соединение → 22C0 ⋀ n-арное логическое и → 905 2303 ⌃ стрелка вверх → 27D1 ⟑ и с точкой 2228 ∨ Логический Или e, ve, ve дизъюнкция → 22C1 ⋁ n-арная логика или → 2304 ⌄ стрелка вниз → 27C7 ⟇ или с точкой внутри 900 20 ∩ 2229 Пересечение = крышка, шляпа → 22C2 ⋂ n-арное пересечение 222A 0 55 Штуцер = стакан → 22C3 ⋃ n-арный штуцер Интегралы
222B20 900 Integral → 0283 ʃ строчная латинская буква esh 222C ∬ Double Integral ≈ 222B ∫ 222D ∭ Тройной интеграл → 2A0C ⨌ Четверной интегральный оператор ≈ 222B ∫ 222B ∫21 222E ∮ Contour Integral → 2A15 ⨕ интеграл вокруг точечного оператора 222F ∯ Surface Integral Surface Integral ≈ 222E ∮ 222E ∮ 2230 ∰ Интеграл по объему ≈ 222E 5 9050 E ∮ 2231 ∱ Интеграл по часовой стрелке 2232 ∲ Контурный интеграл по часовой стрелке 2233 ∳ Контур против часовой стрелки стрелки не меняются местами при зеркальном отображении макета Разные математические символы
2234 ∴ Следовательно, → 26EC ⛬ историческое место 2235 ∵ Потому что Отношения
2236 ∶ Соотношение • предпочтительнее 003 для denotA 003 Использование деления или шкалы в математическом использовании → 003A : двоеточие 2237 ∷ Пропорция Оператор
905 ∸ Точка минус = вычитание насыщения • иногда указывается как обозначение симметричной разницы множеств, но 2206 ∆ является предпочтительным Отношение
2239 ∹ Избыток Оператор
223A ∺ Геометрическая пропорция 22 3B ∻ Homothetic → 2A6B ⩫ тильда с растущими точками 223C ∼ 1 Tilde Operator = изменяется с (пропорционально) = разница между = аналогично = не = цикл = APL-тильда → 007E ~ тильда → 00AC ¬ без знака → 02DC ˜ маленькая тильда 223D ∽ Перевернутая тильда = ленивый S ленивый перевернутый тильда и ленивый S - варианты глифов 223E ∾ Inverted Lazy S = наиболее положительный Разное математический символ 223F Синусоидальная волна = переменного тока Оператор
2240 ≀ Венок Отношения 2241 ≁ Not Tilde ≡ 223C ∼ 0338 ◌̸ 2242 ≂us 2243 ≃ Асимптотически равно 2244 ≄ Не асимптотически равно ≡ 2243 8 2243 9008 900 2245 ≅ Приблизительно равно → 2A70 ⩰ примерно равно или равно 2246 ≆ Фактически примерно равно Кому 9002 0 ≇ 2247 Ни приблизительно, ни фактически не равно ≡ 2245 ≅ 0338 ◌̸ 2248 ≈ Почти равно 21 = асимптотика до 2249 ≉ Не почти равно ≡ 2248 ≈ 224 0338 900A21 ≊ Почти равно или равно 224B ≋ Тройная тильда 224C ≌ Все равно перевернутая тильда и ленивый S - варианты глифов 224 D ≍ Эквивалентно 224E ≎ Геометрически эквивалентно 224F ≏ Разница между 9055 Приближается к пределу 2251 ≑ Геометрически равно 2252 ≒ Приблизительно равно или Изображение равно = 2253 ≓ Изображение или приблизительно равно 2254 ≔ Двоеточие равно 2255 ≕ 1 1 2256 ≖ Кольцо равно 2257 ≗ Кольцо равно = примерно равно 2258 ≘ 1 Соответствует 2259 ≙ Оценки = соответствует 225A ≚ Эквивалентно 21 900B Звезда равно 225C ≜ Дельта равна = равноуглово = равно по определению 90 225D ≝ 9 0554 Равно по определению 225E ≞ Измерено по 225F ≟ Опрошено Равно 2260 4 Не равно 4 Не равно 4 Не равно → 003D = знак равенства → 01C2 ǂ альвеолярный щелчок латинской буквы ≡ 0338 ◌̸ 2261 ≡ Идентично 2262 ≢ Не идентично ≡49 905 905 0338 ◌̸ 2263 ≣ Строго эквивалентно 2264 ≤ Меньше или равно 2265 ≥ Больше или равно Меньше, чем больше равно 2267 ≧ Больше, чем больше, равно 2268 ≨ Меньше, но не равно 2269 ≩ Больше, чем, но не равно 226A ≪ Намного меньше → 00AB «с двумя направлениями влево угловая кавычка 226B ≫ Намного больше 90 021 → 00BB »двойные угловые кавычки, указывающие вправо 226C ≬ Между = истец, количественный 226D ≭ Не эквивалентно ≡ 224D ≍ 0338 ◌̸ 226E ≮ 1 Не менее 1 Не менее ≡ 003C < 0338 ◌̸ 226F ≯ Не больше ≡ 8 003E ◌̸ 2270 ≰ Ни меньше, ни Равно ≡ 2264 ≤ 0338 ◌̸ 2271 ≱ Ни больше, ни равно 2265 ≥ 0338 ◌̸ 2272 ≲ Меньше чем или эквивалентно 2273 ≳ Больше чем 21 19 2274 ≴ Ни менее чем, ни эквивалент ≡ 2272 ≲ 0338 ◌̸ 2275 ≵ Ни один из них -Чем не эквивалентно ≡ 2273 ≳ 0338 ◌̸ 2276 ≶ Меньше или больше 2277 ≷ Больше или меньше 2278 ≸ Ни меньше, ни больше ≡ 2276 ≶ 0338 ◌̸ 2279 ≹ Ни больше, ни -Чем ≡ 2277 ≷ 0338 ◌̸ 227A ≺ Перед ранг ниже → 22B0 ⊰ предшествует по отношению 227B ≻ Успех = ранг выше, чем → 22B1 ⊱ успех в соответствии с отношениями 21 900 предшествует или равно 227D ≽ Успешно или равно 227E ≾ предшествует или эквивалентно 227F20 5 Или эквивалентно 2280 ⊀ Не предшествует ≡ 227A ≺ 0338 ◌̸ 2281 905 905 Не удается ≡ 227B ≻ 0338 ◌̸ 2282 ⊂ Подмножество из = включено в набор 2E26 ⸦ левый боковой u-образный кронштейн 2283 ⊃ Надмножество = входит в набор → 90 2E27 ⸧ правый боковой u-образный кронштейн 2284 ⊄ Не является подмножеством ≡ 2282 ⊂ 0338 ◌̸0 8520 ⊅ Не является расширением 9002 1 ≡ 2283 ⊃ 0338 ◌̸ 2286 ⊆ Подмножество или равно 2287 ⊇ ⊇ Надмножество 21 или равно 900 2288 ⊈ Ни подмножество, ни равное ≡ 2286 ⊆ 0338 ◌̸ 2289 2289 Надмножество не равно ≡ 2287 ⊇ 0338 ◌̸ 228A ⊊ Подмножество не равно 90 ⊋ Надмножество с Не равно Операторы
900 20 228C ⊌ Multiset 228D ⊍ Multiset Умножение → 2A03 ⨃ n-ary union → 2A40 ⩀ пересечение с точкой 228E ⊎ Multiset Union = z добавление сумки обозначений → 2A04 ⨄ Обычный оператор объединения с plus Взаимосвязи
228F ⊏ Квадратное изображение 2290 Квадрат Оригинал 2291 ⊑ Квадратное изображение или равно 2292 ⊒ Квадратное изображение или равно Операторы
2293 Квадрат → 2A05 ⨅ Оператор прямого квадратного пересечения 2294 ⊔ Квадратная чашка → 2A06 n -арикс квадратного оператора 2295 ⊕ Circled Plus = прямая сумма = вектор, указывающий на страницу → 2A01 ⨁ н-р. y обведен плюс оператор → 1F728 🜨 алхимический символ для Verdigris 2296 ⊖ Минус в кружке симметричная разница → 29B5 ⦵ круг с горизонтальной полосой → 1F714 🜔 алхимический символ соли 2297 Времена в кружке = тензорное произведение = вектор, указывающий на страницу → 26D2 ⛒ пересекающиеся полосы в кружке → 2A02 ⨂ n-ary circled times operator → 2BBE ⮾ circled x 2298 ⊘ Circled Division Slash 2299 ⊙ Circled Dot Operator = direct product = vector pointing out of page → 0298 ʘ latin letter bilabial click → 2609 ☉ sun → 2A00 ⨀ n-ary circled dot operator 229A ⊚ Circled Ring Operator → 233E ⌾ apl functional symbol circle jot → 25CE ◎ bullseye 229B ⊛ Circled Asterisk Operator → 235F ⍟ apl functional symbol circle star 229C ⊜ Circled Equals = NoDerivatives (symbol used for Creative Commons licenses) → 1F16D 🅭 circled cc 229D ⊝ Circled Dash 229E ⊞ Squared Plus 90 549 229F ⊟ Squared Minus 22A0 ⊠ Squared Times → 2612 ☒ ballot box with x → 26DD ⛝ squared saltire → 1F771 🝱 alchemical symbol for month 22A1 ⊡ Squared Dot Operator → 1F755 🝕 alchemical symbol for urine → 1FBBC 🮼 right open squared dot 22A2 ⊢ Right Tack = turnstile 900 21 = proves, implies, yields = reducible 22A3 ⊣ Left Tack = reverse turnstile = non-theorem, does not yield Miscellaneous mathematical symbols
22A4 ⊤ Down Tack = top → 2E06 ⸆ raised interpolation marker → 1F768 🝨 alchemical symbol for crucible-4 22A5 ⊥ Up Tack = base, bottom → 27C2 ⟂ perpendicular Relations
22A6 ⊦ Assertion = reduces to 22A7 ⊧ Models 22A8 ⊨ True = statement is true, valid = is a tautology = satisfies = results in 9 0020 ⊩ 22A9 Forces 22AA ⊪ Triple Vertical Bar Right Turnstile 22AB ⊫ Double Vertical Bar Double Right Turnstile 22AC ⊬ Does Not Prove ≡ 22A2 ⊢ 0338 ◌̸ 22AD ⊭ Not True ≡ 22A8 ⊨ 0338 ◌̸ 22AE ⊮ Does Not Force ≡ 22A9 ⊩ 0338 ◌̸ 22AF ⊯ Negated Double Vertical Bar Double Right Turnstile 9 0021 ≡ 22AB ⊫ 0338 ◌̸ 22B0 ⊰ Precedes Under Relation → 227A ≺ precedes 22B1 ⊱ Succeeds Under Relation → 227B ≻ succeeds 22B2 ⊲ Normal Subgroup Of → 25C5 ◅ white left-pointing pointer 22B3 ⊳ Contains As Normal Subgroup → 25BB ▻ white right-pointing pointer 22B4 9 0550 ⊴ Normal Subgroup Of Or Equal To 22B5 ⊵ Contains As Normal Subgroup Or Equal To 22B6 ⊶ Original Of 22B7 ⊷ Image Of 22B8 ⊸ Multimap 22B9 ⊹ Hermitian Conjugate Matrix Operators
22BA ⊺ Intercalate 22BB ⊻ Xor → 26BA ⚺ semisextile 22BC ⊼ Nand → 2305 ⌅ projective → 26BB ⚻ quincunx 22BD ⊽ Nor Miscellaneous mathematical symbols
22BE ⊾ Right Angle With Arc 22BF ⊿ Right Triangle N-ary operators
22C0 ⋀ N-Ary Logical And • also used to denote the universal quantifier → 2227 ∧ logical and 22C1 ⋁ N-Ary Logical Or • also used to denote the existential quantifier → 2228 ∨ logical or 22C2 ⋂ N-Ary Intersection = z notation generalised intersection → 2229 ∩ intersection 22C3 ⋃ N-Ary Union = z notation generalised union → 222A ∪ union Operators
22C4 ⋄ Diamond Operator → 25C7 ◇ white diamond → 2B29 ⬩ black small diamond 22C5 ⋅ Dot Operator • preferred to 00B7 · for denotation of multiplication → 00B7 · middle dot 22C6 ⋆ Star Operator • APL → 066D ٭ arabic five pointed star → 2605 ★ black star → 2B50 ⭐ white medium star 22C7 ⋇ Division Times Relation
22C8 ⋈ Bowtie → 2445 ⑅ ocr bow tie Operators
22C9 ⋉ Left Normal Factor Semidirect Product 22CA ⋊ Right Normal Factor Semidirect Product 22CB ⋋ Left Semidirect Product 22CC ⋌ Right Semidirect Product → 2041 ⁁ caret insertion point Relation
22CD 9055 0 ⋍ Reversed Tilde Equals Logical operators
22CE ⋎ Curly Logical Or 22CF ⋏ Curly Logical And Relations
22D0 ⋐ Double Subset 22D1 ⋑ Double Superset Operators
22D2 ⋒ Double Intersection 22D3 ⋓ Double Union Relations
22D4 ⋔ Pitchfork = proper intersection 9 0021 22D5 ⋕ Equal And Parallel To → 2317 ⌗ viewdata square 22D6 ⋖ Less-Than With Dot 22D7 ⋗ Greater-Than With Dot 22D8 ⋘ Very Much Less-Than 22D9 ⋙ Very Much Greater-Than 22DA ⋚ Less-Than Equal To Or Greater-Than 22DB ⋛ Greater-Than Equal To Or Less-Than 22DC ⋜ Equal To Or Less-Than 22DD ⋝ Equal To O r Greater-Than 22DE ⋞ Equal To Or Precedes 22DF ⋟ Equal To Or Succeeds 22E0 ⋠ Does Not Precede Or Equal ≡ 227C ≼ 0338 ◌̸ 22E1 ⋡ Does Not Succeed Or Equal ≡ 227D ≽ 0338 ◌̸ 22E2 ⋢ Not Square Image Of Or Equal To ≡ 2291 ⊑ 0338 ◌̸ 22E3 ⋣ Not Square Original Of Or Equal To 90 020 ≡ 2292 ⊒ 0338 ◌̸ 22E4 ⋤ Square Image Of Or Not Equal To 22E5 ⋥ Square Original Of Or Not Equal To 22E6 ⋦ Less-Than But Not Equivalent To 22E7 ⋧ Greater-Than But Not Equivalent To 22E8 ⋨ Precedes But Not Equivalent To 22E9 ⋩ Succeeds But Not Equivalent To 22EA ⋪ Not Normal Subgroup Of ≡ 22B2 ⊲ 0338 ◌̸ 22EB 905 50 ⋫ Does Not Contain As Normal Subgroup ≡ 22B3 ⊳ 0338 ◌̸ 22EC ⋬ Not Normal Subgroup Of Or Equal To ≡ 22B4 ⊴ 0338 ◌̸ 22ED ⋭ Does Not Contain As Normal Subgroup Or Equal ≡ 22B5 ⊵ 0338 ◌̸ Matrix ellipses
22EE ⋮ Vertical Ellipsis → 205D ⁝ tricolon → 2026 … horizontal ellipsis → FE19 ︙ presentation form for vertical horizontal ellipsis 22EF ⋯ Midline Horizontal Ellipsis 22F0 ⋰ Up Right Diagonal Ellipsis 22F1 ⋱ Down Right Diagonal Ellipsis Relations
22F2 ⋲ Element Of With Long Horizontal Stroke 22F3 ⋳ Element Of With Vertical Bar At End Of Horizontal Stroke 22F4 ⋴ Small Element Of With Vertical Bar At End Of Horizontal Stroke 22F5 ⋵ Element Of With Dot Above 22F6 ⋶ Element Of With Overbar 22F7 ⋷ Small Element Of With Overbar 22F8 ⋸ Element Of With Underbar 22F9 ⋹ Element Of With Two Horizontal Strokes 22FA ⋺ Contains With Long Horizontal Stroke 22FB ⋻ Contains With Vertical Bar At End Of Horizontal Stroke 22FC ⋼ Small Contains With Vertical Bar At End Of Horizontal Stroke 22FD ⋽ Contains With Overbar 22FE ⋾ Small C ontains With Overbar 22FF ⋿ Z Notation Bag Membership Nemeth Tutorial - Lesson 10.1
Примерно равно
Аналогично знаку, тильда
Соответствует подписи
Пример 1
⠼⠂⠨⠶⠦⠀⠈⠱⠈⠱⠀⠼⠂⠨⠦ Пример 2
⠨⠏⠀⠈⠱⠈⠱⠀⠼⠒⠨⠂⠲ Пример 3
⠫⠞⠀⠠⠁⠠⠃⠠⠉⠀⠈⠱⠀⠫⠞⠀⠠⠭⠠⠽⠠⠵ Пример 4
⠫⠵⠀⠠⠁⠠⠃⠠⠉⠠⠙⠀⠈⠱⠀⠫⠵⠀⠠⠍⠠⠝⠠⠕⠠⠏ Пример 5
⠫⠞⠀⠠⠁⠠⠃⠠⠉⠀⠈⠱⠨⠅⠀⠫⠞⠀⠠⠭⠠⠽⠠⠵ Пример 6
⠐⠠⠁⠠⠃⠣⠱⠻⠀⠈⠱⠨⠅⠀⠐⠠⠉⠠⠙⠣⠱⠻ Пример 7
⠫⠪⠀⠠⠁⠀⠈⠱⠨⠅⠀⠫⠪⠀⠠⠃ Список математических символов Facts for Kids
Обозначение Имя Читать как Значение Пример равенство равно, равно Если x = y, x и y представляют одно и то же значение или вещь. 2 + 3 = 5 определение определяется как Если x≡y, x определяется как другое имя y (a + b) 2 ≡a 2 + 2ab + b 2 примерно равно примерно равно Если x≈y, x и y почти равны. √2≈1,41 неравенство не равно, не равно Если x ≠ y, x и y не представляют одно и то же значение или предмет. 1 + 1 ≠ 3 меньше Если x 4 <5 больше Если x> y, x больше y. 3> 2 намного меньше Если x≪y, x намного меньше y. 1,9999999999 намного больше, чем Если x≫y, x намного больше y. 88979808≫0,001 меньше или равно Если x≤y, x меньше или равно y. 5≤6 и 5≤5 больше или равно Если x≥y, x больше или равно y. 2≥1 и 2≥2 пропорциональность пропорционален Если x∝y, то y = kx для некоторой постоянной k. Если y = 4x, то y∝x и x∝y дополнение плюс x + y - это сумма x и y. 2 + 3 = 5 вычитание минус x-y - это вычитание y из x 5-3 = 2 умножение раз x × y - это произведение x на y 4 × 5 = 20 x · y - это произведение x на y 4 · 5 = 20 отдел разделить на x ÷ y или x / y - деление x на y 20 ÷ 4 = 5 и 20/4 = 5 20/4 = 5 плюс-минус плюс-минус x ± y означает как x + y, так и x-y Уравнение 3 ± √9 имеет два решения: 0 и 6. минус-плюс минус или плюс 4 ± (3∓5) означает как 4+ (3-5), так и 4- (3 + 5) 6∓ (1 ± 3) = 2 или 4 квадратный корень квадратный корень √x - это число, квадрат которого равен x. √4 = 2 или -2 суммирование сумма свыше… от… до… из, сигма совпадает с x 1 + x 2 + x 3 + x k умножение товар более… с… до… из совпадает с x 1 × x 2 × x 3 × x k = 1 × 2 × 3 × 4 × 5 = 120 факториал факториал н! это произведение 1 × 2 × 3... × п 5! = 1 × 2 × 3 × 4 × 5 = 120 материальное значение означает A⇒B означает, что если A истинно, B также должно быть истинным, но если A ложно, B неизвестно. x = 3⇒x 2 = 9, но x 2 = 9⇒x = 3 неверно, потому что x также может быть -3. эквивалент материала тогда и только тогда, когда Если A истинно, B истинно, а если A ложно, B ложно. х = у + 1⇔x-1 = у абсолютное значение абсолютное значение | x | это расстояние вдоль действительной линии (или поперек комплексной плоскости) между x и нулем | 5 | = 5 и | -5 | = 5 параллельно параллельно Если A || B, то A и B параллельны перпендикуляр перпендикулярно Если A⊥B, то A перпендикулярно B соответствие соответствует Если A≅B, то форма A соответствует форме B (имеет те же размеры) золотое сечение золотое сечение Золотое сечение - это иррациональное число, равное (1 + √5) ÷ 2 или приблизительно 1.6180339887. бесконечность бесконечность ∞ - это число больше любого действительного числа. набор членства является элементом a∈S означает, что a является элементом множества S 3.5∈ℝ, 1∈ℕ, 1+ i ∈ℂ не является элементом a∉S означает, что a не является элементом набора S 2.1∉ℕ, 1+ и ∉ℝ Комплект скоб набор {a, b, c} - это набор, состоящий из a, b и c ℕ = {0,1,2,3,4,5 ...} Натуральные числа N ℕ обозначает набор натуральных чисел {0,1,2,3,4,5 ...} Целые числа Z ℤ обозначает набор целых чисел (-3, -2, -1,0,1,2,3...) Рациональные числа Q ℚ обозначает набор рациональных чисел (числа, которые можно записать как дробь a / b, где a∈ℤ, b∈ℕ) 8.323∈ℚ, 7∈ℚ, π∉ℚ Реальные числа R ℝ обозначает набор действительных чисел π∈ℝ, 7∈ℝ, √ (-1) ∉ℝ Комплексные числа С ℂ обозначает набор комплексных чисел √ (-1) ∈ℂ Среднее бар, бар x - среднее (среднее) x i , если x = {1,2,3}, то x̄ = 2 комплексное сопряжение комплексное сопряжение x Если x = a + bi, то x̄ = a - bi, где i = √ (-1) х = -4 + 5.3i, x̄ = -4 - 5,3i Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞
Пример применения
Возведение в степень и дробь