Символ неравно – ≠ — Не равный (U+2260)

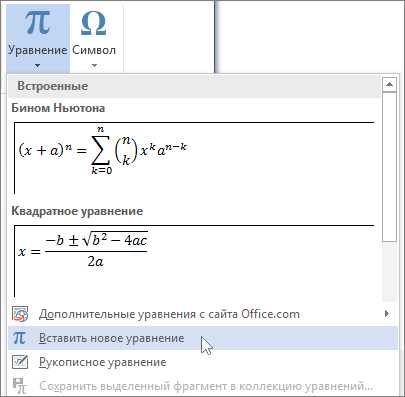
≠ — Не равный (U+2260)

Начертание символа «Не равный» в разных шрифтах

≠

Ваш браузер

Описание символа

Не равный. Математические операторы.

Связанные символы

Кодировка

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	E2 89 A0	226 137 160	14846368	11100010 10001001 10100000
UTF-16BE	22 60	34 96	8800	00100010 01100000
UTF-16LE	60 22	96 34	24610	01100000 00100010
UTF-32BE	00 00 22 60	0 0 34 96	8800	00000000 00000000 00100010 01100000
UTF-32LE	60 22 00 00	96 34 0 0	1612840960	01100000 00100010 00000000 00000000

unicode-table.com

Знак неравенства Википедия

Символы со сходным начертанием: 二 · ニ · ═

Знак равенства
=
Изображение
	equals sign
Юни	U+003D
HTML-	или
UTF-16	0x3D
	%3D

Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя идентичными по своему значению выражениями.

История появления[ | ]

Знак равенства в современной форме создал математик Роберт Рекорд (Robert Recorde, 1510—1558) в своём труде The Whetstone of Witte (1557). Он обосновал применение двух параллельных штрихов так (орфография оригинала — ранненовоанглийский): «…bicause noe 2 thynges can be moare equalle», то есть «никакие другие две вещи не могут быть более равными». До этого в античной и средневековой математике равенство обозначалось словесно (например

est egale). Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал, чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. В континентальной Европе знак «=» был введён Лейбницем только на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда.

Таблица математических знаков (символов) эквивалентности с ами Unicode[

ru-wiki.ru

Как поставить знак не равно в Excel

Если такие знаки сравнения, как «больше» (>) и «меньше» (<) довольно легко находятся на клавиатуре компьютера, то с написанием элемента «не равно» (≠) возникают проблемы, так как его символ на ней отсутствует. Этот вопрос касается всех программных продуктов, но особенно он актуален для приложения Microsoft Excel, так как в нём проводятся различные математические и логические вычисления, для которых этот знак необходим. Давайте узнаем, как поставить данный символ в Экселе.

Написание знака «не равно»

Прежде всего, нужно сказать, что в Экселе существует два знака «не равно»:

«<>» и «≠». Первый из них используется для вычислений, а второй исключительно для графического отображения.

Символ «<>»

Элемент «<>» применяется в логических формулах Эксель, когда нужно показать неравенство аргументов. Впрочем, его можно применять и для визуального обозначения, так как он все больше входит в обиход.

Наверное, уже многие поняли, что для того, чтобы набрать символ «<>», нужно сразу набрать на клавиатуре знак «меньше» (<), а потом элемент «больше» (>). В итоге получается вот такая надпись: «<>».

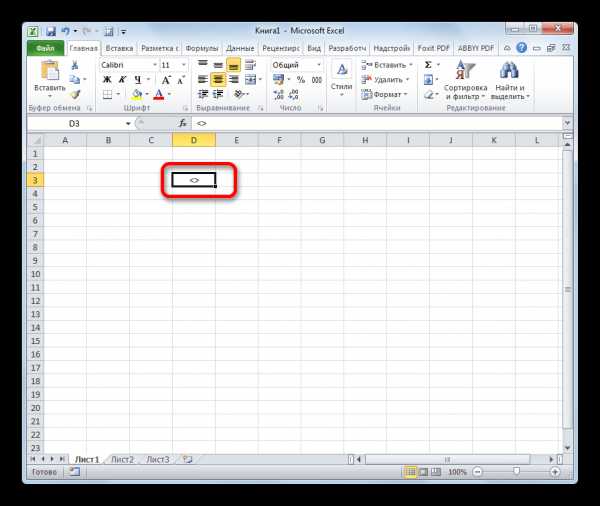
Существует ещё один вариант набора данного элемента. Но, при наличии предыдущего, он, безусловно, покажется неудобным. Смысл его использовать есть лишь в том случае, если по какой-либо причине клавиатура оказалась отключена.

1. Выделяем ячейку, куда должен быть вписан знак. Переходим во вкладку «Вставка». На ленте в блоке инструментов «Символы» жмем на кнопку с наименованием «Символ».



2. Открывается окно выбора символов. В параметре «Набор» должен быть выставлен пункт «Основная латиница». В центральной части окна находится огромное количество различных элементов, среди которых далеко не все есть на стандартной клавиатуре ПК. Чтобы набрать знак «не равно» сначала кликаем по элементу «<», затем нажимаем на кнопку «Вставить». Сразу же после этого жмем «>» и опять на кнопку «Вставить». После этого окно вставки можно закрывать, нажав белый крестик на красном фоне в левом верхнем углу.

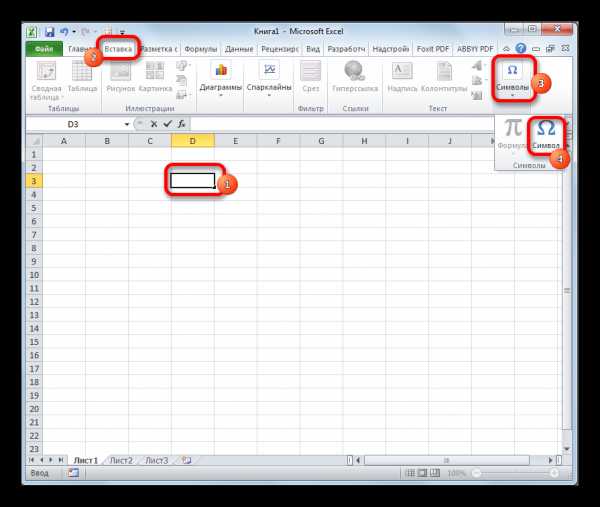
Таким образом, наша задача полностью выполнена.

Символ «≠»

Знак «≠» используется исключительно в визуальных целях. Для формул и других вычислений в Excel его применять нельзя, так как приложение не распознаёт его, как оператора математических действий.

В отличие от символа «<>» набрать знак «≠» можно только при помощи кнопки на ленте.

1. Кликаем по ячейке, в которую планируется вставить элемент. Переходим во вкладку «Вставка». Жмем на уже знакомую нам кнопку «Символ».



2. В открывшемся окне в параметре «Набор» указываем «Математические операторы». Ищем знак «≠» и кликаем по нему. Затем жмем на кнопку «Вставить». Закрываем окно тем же способом, что и предыдущий раз, нажав на крестик.

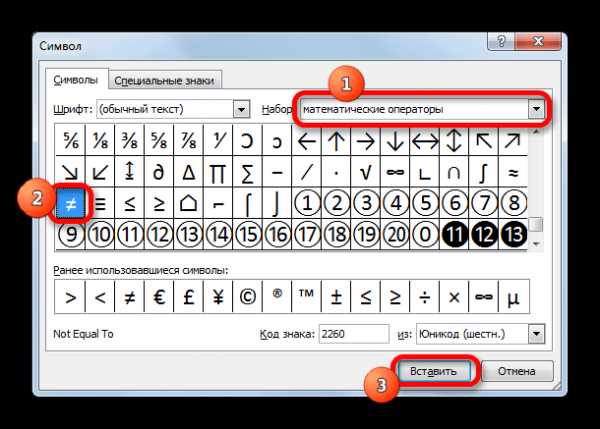
Как видим, элемент «≠» в поле ячейки вставлен успешно.

Мы выяснили, что в Эксель существует два вида символов «не равно». Один из них состоит из знаков «меньше» и «больше», и используется для вычислений. Второй (≠) – самодостаточный элемент, но его использование ограничивается только визуальным обозначением неравенства.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Таблица математических символов

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования.

Кроме указанных символов, иногда используются их зеркальные отражения, например, обозначает то же, что и

Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.

таблица математических символов, таблица символов, таблица символов ascii, таблица символов html, таблица символов html кода free, таблица символов в ворде, таблица символов для ников, таблица символов на клавиатуре, таблица символов на клавиатуре для вк, таблица символов юникода

Таблица математических символов что, Таблица математических символов кто, Таблица математических символов описание

Символ (TeX)	Символ (Юникод)	Название	Значение	Пример
		Произношение
		Раздел математики
	⇒ → ⊃	Импликация, следование	означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.).	верно, но неверно (так как также является решением).
		«влечёт» или «если…, то»
		везде
	⇔	Равносильность	означает « верно тогда и только тогда, когда верно».
		«если и только если» или «равносильно»
		везде
	∧	Конъюнкция	истинно тогда и только тогда, когда и оба истинны.	, если  — натуральное число.
		«и»
		Математическая логика
	∨	Дизъюнкция	истинно, когда хотя бы одно из условий и истинно.	, если  — натуральное число.
		«или»
		Математическая логика
	¬	Отрицание	истинно тогда и только тогда, когда ложно .
		«не»
		Математическая логика
	∀	Квантор всеобщности	обозначает « верно для всех ».
		«Для любых», «Для всех», «Для всякого»
		Математическая логика
	∃	Квантор существования	означает «существует хотя бы один такой, что верно »	(подходит число 5)
		«существует»
		Математическая логика
	=	Равенство	обозначает « и обозначают одно и то же значение».	1 + 2 = 6 − 3
		«равно»
		везде
	:= :⇔	Определение	означает « по определению равен ». означает « по определению равносильно »	(определение гиперболического косинуса) (определение исключающего «ИЛИ»)
		«равно/равносильно по определению»
		везде
	{ }	Множество элементов	означает множество, элементами которого являются , и .	(множество натуральных чисел)
		«Множество…»
		Теория множеств
	{|}	Множество элементов, удовлетворяющих условию	означает множество всех таких, что верно .
		«Множество всех… таких, что верно…»
		Теория множеств
	∅ {}	Пустое множество	и означают множество, не содержащее ни одного элемента.
		«Пустое множество»
		Теория множеств
	∈ ∉	Принадлежность/непринадлежность к множеству	означает « является элементом множества » означает « не является элементом множества »
		«принадлежит», «из» «не принадлежит»
		Теория множеств
	⊆ ⊂	Подмножество	означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
		«является подмножеством», «включено в»
		Теория множеств
	⊇ ⊃	Надмножество	означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
		«является надмножеством», «включает в себя»
		Теория множеств
	⊊	Собственное подмножество	означает и .
		«является собственным подмножеством», «строго включается в»
		Теория множеств
	⊋	Собственное надмножество	означает и .
		«является собственным надмножеством», «строго включает в себя»
		Теория множеств
	∪	Объединение	означает множество элементов, принадлежащих и
		«Объединение … и …», «…, объединённое с …»
		Теория множеств
	⋂	Пересечение	означает множество одинаковых элементов, принадлежащих и , и .
		«Пересечение … и … «, «…, пересечённое с …»
		Теория множеств
	\	Разность множеств	означает множество элементов, принадлежащих , но не принадлежащих .
		«разность … и …», «минус», «… без …»
		Теория множеств
	→	Функция (отображение)	означает функцию с областью определения и областью значений .	Функция , определённая как
		«из … в …»,
		везде
	↦	Отображение	означает, что образом после применения функции будет .	Функцию, определённую как , можно записать так:
		«отображается в»
		везде
	N или ℕ	Натуральные числа	означает множество или реже (в зависимости от ситуации).
		«Эн»
		Числа
	Z или ℤ	Целые числа	означает множество
		«Зед»
		Числа
	Q или ℚ	Рациональные числа	означает
		«Ку» или «Къю»
		Числа
	R или ℝ	Вещественные (действительные) числа	означает множество всех пределов последовательностей из	( — мнимая единица: )
		«Эр»
		Числа
	C или ℂ	Комплексные числа	означает множество
		«Це»
		Числа
	H или	Кватернионы	означает множество
		«Аш»
		Числа
	< >	Сравнение	обозначает, что строго меньше . означает, что строго больше .
		«меньше чем», «больше чем»
		Отношение порядка
или или	⩽ или ≤ ⩾ или ≥	Сравнение	означает, что меньше или равен . означает, что больше или равен .
		«меньше или равно»; «больше или равно»
		Отношение порядка
	≈	Приблизительное равенство	с точностью до 10−3 означает, что 2,718 отличается от не больше чем на 10−3.	с точностью до 10−7.
		«приблизительно равно»
		Числа
	√	Арифметический квадратный корень	означает неотрицательное действительное число, которое в квадрате даёт .
		«Корень квадратный из …»
		Числа
	∞	Бесконечность	и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел.
		«Плюс/минус бесконечность»
		Числа
	| |	Абсолютная величина (абсолютное значение, модуль) числа, или мощность множества	обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов .
		«Модуль»; «Мощность»
		Числа и Теория множеств
	∑	Сумма (набора чисел), сумма ряда	означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из .
		«Сумма … по … от … до …»
		Арифметика, Математический анализ
	∏	Произведение	означает «произведение для всех от 1 до », то есть
		«Произведение … по … от … до …»
		Арифметика
	!	Факториал	означает произведение всех натуральных чисел от 1 до включительно, то есть
		« факториал»
		Комбинаторика
	∫	Интеграл	означает «интеграл от до функции от по переменной ».
		«Интеграл (от … до …) функции … по (или d)…»
		Математический анализ
	df/dx f'(x)	Производная	или означает «(первая) производная функции от по переменной ».
		«Производная … по …»
		Математический анализ
	∂f/∂y	Частная производная	означает «(первая) частная производная функции от переменных по переменной ».
		«Частная производная … по …»
		Математический анализ
	dnf/dxn f(n)(x)	Производная -го порядка	или (во втором случае если  — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ».
		«-я производная … по …»
		Математический анализ

www.turkaramamotoru.com

Знак равенства — это… Что такое Знак равенства?

=
Именно так должен выглядеть этот символ
Название символа	Знак равенства
Юникод	U+003D
HTML	=
UTF-8	3D
Заглавная форма	=
Строчная форма	=
Группа в Юникоде	ASCII
{{{метка9}}}	{{{текст9}}}
{{{метка10}}}	{{{текст10}}}

Знак равенства (=) в математике, в логике и других точных науках пишут между двумя идентичными по своему значению выражениями.

История появления

Знак равенства в современной форме создал математик Роберт Рекорд (Robert Recorde, 1510—1558) в своём труде The Whetstone of Witte (1557). Он обосновал применение двух параллельных штрихов так (на староанглийском): «…bicause noe 2 thynges can be moare equalle», то есть «никакие другие две вещи не могут быть более равными». До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. В континентальной Европе знак «=» был введён Лейбницем только на рубеже XVII—XVIII веков, то есть более чем через 100 лет, после смерти впервые использовавшего его для этого Роберта Рекорда

Таблица математических знаков (символов) эквивалентности с кодами Unicode

Необходимо добавить символы: 1 подобия фигур, 2 равенства с точностью до зеркального подобия, 3 равенства «почти всюду»

Похожие символы

• ≠, !=, либо <> — не равно.
• ≃, ≈, либо ~ — «приблизительно равно». Используется при обозначении двух величин, разницей между которыми в данной задаче можно пренебречь.
• ~ — «пропорционально». Иногда используется для обозначения пропорциональности двух величин или подобия в геометрии.
• ≡ — «тождественно равно». Используется для обозначения двух идентичных (равных при любых значениях входящих параметров) выражений.
•  := — часто используется для обозначения оператора присваивания.
• ≌ — подобие фигур. Используется для обозначения подобных фигур в геометрии.

Применение в информатике

В языках программирования символ = чаще всего используется для операций сравнения и/или присваивания. В некоторых языках (например, Basic) символ используется для обеих операций, в зависимости от контекста. В языках C, PHP и т. п. = обозначает присваивание, равенство записывается как ==. В Perl, кроме того, операторы для сравнения строк отличаются от операторов для сравнения чисел, равенство строк проверяет eq. В Pascal, напротив, = обозначает равенство, присваивание обозначается :=.

Литература

dic.academic.ru

Кто знает, существует ли в математике специальный символ, который обозначает разницу?

«дельта» обозначает разницу

Ой, точно дельта!! ! 🙂

Смотря какая разница имеется ввиду. Если два объекта — разные, то знак «неравно» — перечёркнутое равенство. (Возможно, что разными символами обозначен один и тот же объект, тогда равно или тождественно равно) . Если каким-то другим способом измеряется различие объектов и это различие может быть выражено числом, то (при выполнении ещё нескольких условий) , говорят, что на множестве объектов «введена метрика». Ввести метрику можно разными способами (на одном множестве определить много метрик) , Часто «расстояние» в выбранной метрике обозначают буквой «ро» греческой и в скобках записывают обозначения объектов. Если на множестве определены операции «сложение» и обратная «вычитание» и введена метрика, то часто разницу (расстояние) обозначают как модуль у действительных чисел |x-y|, Иногда в двойных палочках — и называют «нормой» (Норма — расстояние до нулевого элемента) На множестве действительных чисел разницу часто означают как заглавную греческую дельта. А меняющуюся разницу, например разницу меджу функциями (не в точке — здесь будет разница чисел) , а «вообще» называют «вариация» и часто обозначают греческой дельта — маленькой. Даже «сигма» — это сейчас общепринятый знак, но не «законодательно утверждённый» В математике нет твёрдо установленных правил. Даже символы плюс и минус могут использоваться совсем в другом смысле, чем «учат в школе» В статьях и книгах обычно разъясняют смысл используемых знаков. Такое объяснение — требование стандарта.

<img src=»//otvet.imgsmail.ru/download/192238791_9e857ab4795b02f337f5a177c5fd1adb_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/192238791_9e857ab4795b02f337f5a177c5fd1adb_120x120.jpg» data-big=»1″>

Что означает буква DELTA над знаком = равенства

touch.otvet.mail.ru

Вставка математических знаков — Word

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

В Word можно вставлять математические символы в уравнения и текст.

1. На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

   

2. В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

3. Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.

4. Щелкните нужный символ.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Набор символов	Подгруппа	Определение
Основные математические символы	Нет	Часто используемые математические символы, такие как > и <
Греческие буквы	Строчные буквы	Строчные буквы греческого алфавита
	Прописные буквы	Прописные буквы греческого алфавита
Буквоподобные символы	Нет	Символы, которые напоминают буквы
Операторы	Обычные бинарные операторы	Символы, обозначающие действия над двумя числами, например + и ÷
	Обычные реляционные операторы	Символы, обозначающие отношение между двумя выражениями, такие как = и ~
	Основные N-арные операторы	Операторы, осуществляющие действия над несколькими переменными
	Сложные бинарные операторы	Дополнительные символы, обозначающие действия над двумя числами
	Сложные реляционные операторы	Дополнительные символы, обозначающие отношение между двумя выражениями
Стрелки	Нет	Символы, указывающие направление
Отношения с отрицанием	Нет	Символы, обозначающие отрицание отношения
Наборы знаков	Наборы знаков	Математический шрифт Script
	Готические	Математический шрифт Fraktur
	В два прохода	Математический шрифт с двойным зачеркиванием
Геометрия	Нет	Часто используемые геометрические символы

Дополнительные сведения

Вставка флажка или другого символа

support.office.com