Арабские цифры ① ❶ ⓵ ¼ 𝟙 𝟏 в разном начертании
Римские
Ⅰ – 1 ; ⅩⅠ — 11
Ⅱ – 2 ; ⅩⅡ — 12
Ⅲ – 3 ; ⅩⅢ — 13
Ⅳ – 4 ; ⅩⅣ — 14
Ⅴ – 5 ; ⅩⅤ — 15
Ⅵ – 6 ; ⅩⅥ — 16
Ⅶ – 7 ; ⅩⅦ — 17
Ⅷ – 8 ; ⅩⅧ — 18
Ⅸ – 9 ; ⅩⅨ — 19
Ⅹ – 10 ; ⅩⅩ — 20
Ⅽ – 50 ; ⅩⅩⅠ — 21
Ⅾ — 100
Ⅿ — 500
ↁ — 1000
ↂ – 10000
Соответствие арабских цифр
Арабские (арбская письменность) = Индийские (в письменности деванагари) = Арабские (понятные нам)
٠ = ० = 0
١ = १ = 1
٢ = २ = 2
٣ = ३ = 3
٤ = ४ = 4
٥ = ५ = 5
٦ = ६ = 6
٧ = ७ = 7
٨ = ८ = 8
٩ = ९ = 9
Данная страница содержит красивые арабские цифры, которые не напечатать с клавиатуры. Их можно скопировать и вставить туда, где нельзя изменить шрифт (в соц. сетях). Кроме цифр, которыми пользуются европейцы, тут есть и настоящие — те что применяют сами арабы.
Немного истории. Считается, что арабская система счисления зародилась в Индии, примерно, в V веке. Хотя, возможно, что ещё раньше и в Вавилоне. Арабскими цифры называются потому, что в Европу пришли от арабов. Сначала, в мусульманскую часть Испании, а в X веке уже и папа римский Сильвестр II призывал забросить громоздкую латинскую запись. Серьёзным толчком к распространению арабских цифр стал перевод на латинский язык книги Аль-Хорезми «Об индийском счёте».
Индо-арабская система записи чисел является десятичной. Любое число составляется из 10 знаков. Юникод, кстати, использует шестнадцатеричные числа. Удобнее римской она потому, что позиционная. В таких системах, величина которую обозначает цифра зависит от её положения в числе. В числе 90 цифра 9 значит девяносто, а в числе 951 – девятьсот.
Если для кого-то эти символы слишком большие, то маленькие цифры лежат рядом. Маленькие буквы тоже в наличии.
① — Цифра один в круге: U+2460
Значение символа
Цифра один в круге. Обрамлённые буквы и цифры.
Символ «Цифра один в круге» был утвержден как часть Юникода версии 1.
Свойства
| Версия | 1.1 |
| Блок | Обрамлённые буквы и цифры |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2460 |
| Простое изменение регистра | 2460 |
Похожие символы
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 91 A0 | 226 145 160 | 14848416 | 11100010 10010001 10100000 |
| UTF-16BE | 24 60 | 36 96 | 9312 | 00100100 01100000 |
| UTF-16LE | 60 24 | 96 36 | 24612 | 01100000 00100100 |
| UTF-32BE | 00 00 24 60 | 0 0 36 96 | 9312 | 00000000 00000000 00100100 01100000 |
| UTF-32LE | 96 36 0 0 | 1612972032 | 01100000 00100100 00000000 00000000 |
② — Цифра два в круге: U+2461
Значение символа
Обрамлённые буквы и цифры.Символ «Цифра два в круге» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Обрамлённые буквы и цифры |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2461 |
| Простое изменение регистра |
Похожие символы
Кодировка
| Кодировка | dec (bytes) | dec | binary | |
|---|---|---|---|---|
| UTF-8 | E2 91 A1 | 226 145 161 | 14848417 | 11100010 10010001 10100001 |
| UTF-16BE | 24 61 | 36 97 | 9313 | 00100100 01100001 |
| UTF-16LE | 61 24 | 97 36 | 24868 | 01100001 00100100 |
| UTF-32BE | 00 00 24 61 | 0 0 36 97 | 9313 | 00000000 00000000 00100100 01100001 |
| UTF-32LE | 61 24 00 00 | 97 36 0 0 | 1629749248 | 01100001 00100100 00000000 00000000 |
Поиск рисунков Меню
Горячая десятка
Фото — Картинки Скуби-Ду и ОборотеньВоздушная Езда КирбиСнупиФрида из «Снупи»Криг «Borderlands»Безумный Фред из «Кураж — трусливый пёс»Праздники | Рисунки символами » Алфавит, Буквы, Цифры из символов » Цифры символами Алфавит, Буквы, Цифры — картинки символами
Маленькие Сердечки Любовь Смайлики Девушки Мемы Статусы Аниме Кошки Собаки Цветы Праздники Ангелы Тату Авто Мотоциклы Самолёты Корабли Танки Оружие Спорт Анимация Gif Надписи Женские Мужские имена Дома Еда Люди Мультфильмы Фильмы Музыка Черепа Картинки из Смайликов Животные Лучшие Символы ✎ Рисовать
| Генераторы Ascii
Menu
Почитай-ка
Видео Приколы
| ||||||||||||||||||||
Bean (ASCII Text Art)
07.2010 » просмотров: 12474
T 
Bean (ASCII Text Art) Вставка символов и знаков на основе латинского алфавита в кодировке ASCII или Юникод
Вставка символа ASCII или Юникода в документ
Если вам нужно ввести только несколько специальных знаков или символов, можно использовать таблицу символов или сочетания клавиш.
Список символов ASCII см. в следующих таблицах или статье Вставка букв национальных алфавитов с помощью сочетаний клавиш.
Примечания:
-
Многие языки содержат символы, которые не удалось сжатить, в 256-символьный набор extended ACSII. Таким образом, существуют варианты ASCII и Юникода, которые должны включать региональные символы и символы, и см. таблицы кодов символов Юникода по сценариям.
-
Если у вас возникают проблемы с вводом кода необходимого символа, попробуйте использовать таблицу символов.
Вставка символов ASCII
Чтобы вставить символ ASCII, нажмите и удерживайте клавишу ALT, вводя код символа. Например, чтобы вставить символ градуса (º), нажмите и удерживайте клавишу ALT, затем введите 0176 на цифровой клавиатуре.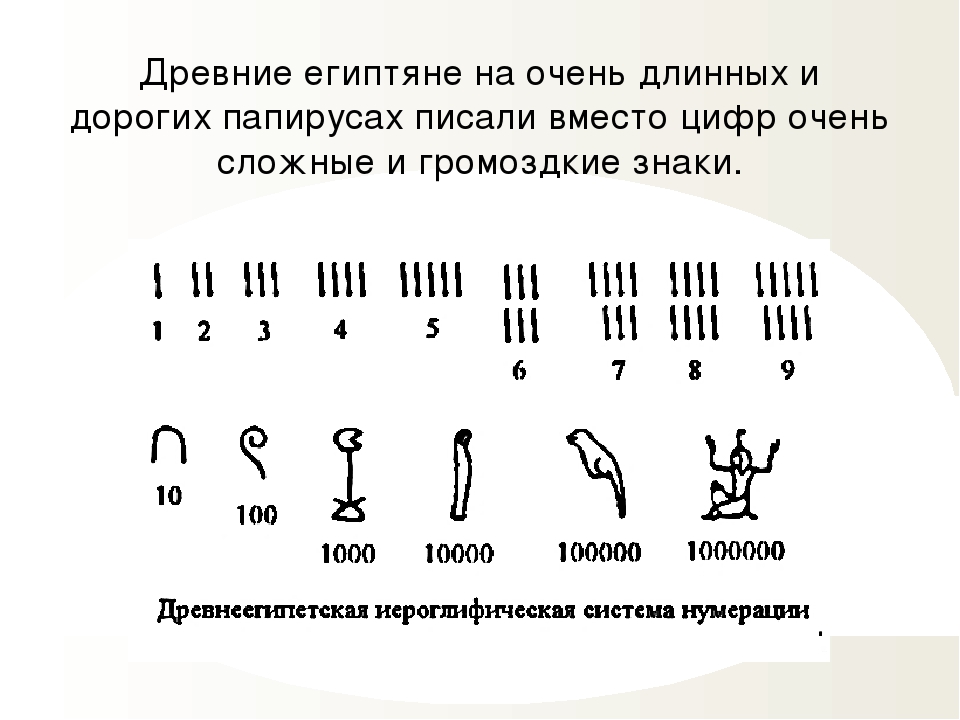
Для ввода чисел используйте цифровую клавиатуру, а не цифры на основной клавиатуре. Если на цифровой клавиатуре необходимо ввести цифры, убедитесь, что включен индикатор NUM LOCK.
Вставка символов Юникода
Чтобы вставить символ Юникода, введите код символа, затем последовательно нажмите клавиши ALT и X. Например, чтобы вставить символ доллара ($), введите 0024 и последовательно нажмите клавиши ALT и X. Все коды символов Юникода см. в таблицах символов Юникода, упорядоченных по наборам.
Важно: Некоторые программы Microsoft Office, например PowerPoint и InfoPath, не поддерживают преобразование кодов Юникода в символы. Если вам необходимо вставить символ Юникода в одной из таких программ, используйте таблицу символов.
Примечания:
-
Если после нажатия клавиш ALT+X отображается неправильный символ Юникода, выберите правильный код, а затем снова нажмите ALT+X.
-
Кроме того, перед кодом следует ввести «U+». Например, если ввести «1U+B5» и нажать клавиши ALT+X, отобразится текст «1µ», а если ввести «1B5» и нажать клавиши ALT+X, отобразится символ «Ƶ».
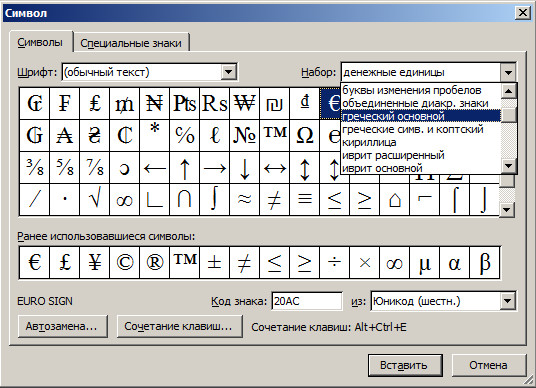
Использование таблицы символов
Таблица символов — это программа, встроенная в Microsoft Windows, которая позволяет просматривать символы, доступные для выбранного шрифта.
С помощью таблицы символов можно копировать отдельные символы или группу символов в буфер обмена и вставлять их в любую программу, поддерживающую отображение этих символов. Открытие таблицы символов
-
В Windows 10 Введите слово «символ» в поле поиска на панели задач и выберите таблицу символов в результатах поиска.
-
В Windows 8 Введите слово «символ» на начальном экране и выберите таблицу символов в результатах поиска.
-
В Windows 7: Нажмите кнопку Пуск, а затем последовательно выберите команды Программы, Стандартные, Служебные и Таблица знаков.
Знаки группются по шрифтам. Щелкните список шрифтов, чтобы выбрать набор символов. Чтобы выбрать символ, щелкните его, нажмите кнопку «Выбрать», щелкните в документе правую кнопку мыши в том месте, где он должен быть, а затем выберите «Вировать».
К началу страницы
Коды часто используемых символов
Полный список символов см.
в таблице символов на компьютере, таблице кодов символов ASCII или таблицах символов Юникода, упорядоченных по наборам.
|
Глиф |
Код |
Глиф |
Код |
|---|---|---|---|
|
Денежные единицы |
|||
|
£ |
ALT+0163 |
¥ |
ALT+0165 |
|
¢ |
ALT+0162 |
$ |
0024+ALT+X |
|
€ |
ALT+0128 |
¤ |
ALT+0164 |
|
Юридические символы |
|||
|
© |
ALT+0169 |
® |
ALT+0174 |
|
§ |
ALT+0167 |
™ |
ALT+0153 |
|
Математические символы |
|||
|
° |
ALT+0176 |
º |
ALT+0186 |
|
√ |
221A+ALT+X |
+ |
ALT+43 |
|
# |
ALT+35 |
µ |
ALT+0181 |
|
< |
ALT+60 |
> |
ALT+62 |
|
% |
ALT+37 |
( |
ALT+40 |
|
[ |
ALT+91 |
) |
ALT+41 |
|
] |
ALT+93 |
∆ |
2206+ALT+X |
|
Дроби |
|||
|
¼ |
ALT+0188 |
½ |
ALT+0189 |
|
¾ |
ALT+0190 |
||
|
Знаки пунктуации и диалектные символы |
|||
|
? |
ALT+63 |
¿ |
ALT+0191 |
|
! |
ALT+33 |
‼ |
203+ALT+X |
|
— |
ALT+45 |
‘ |
ALT+39 |
|
« |
ALT+34 |
, |
ALT+44 |
|
. |
ALT+46 |
| |
ALT+124 |
|
/ |
ALT+47 |
\ |
ALT+92 |
|
` |
ALT+96 |
^ |
ALT+94 |
|
« |
ALT+0171 |
» |
ALT+0187 |
|
« |
ALT+174 |
» |
ALT+175 |
|
~ |
ALT+126 |
& |
ALT+38 |
|
: |
ALT+58 |
{ |
ALT+123 |
|
; |
ALT+59 |
} |
ALT+125 |
|
Символы форм |
|||
|
□ |
25A1+ALT+X |
√ |
221A+ALT+X |
К началу страницы
Коды часто используемых диакритических знаков
Полный список глифов и соответствующих кодов см.
в таблице символов.
|
Глиф |
Код |
Глиф |
Код |
|
|---|---|---|---|---|
|
à |
ALT+0195 |
å |
ALT+0229 |
|
|
Å |
ALT+143 |
å |
ALT+134 |
|
|
Ä |
ALT+142 |
ä |
ALT+132 |
|
|
À |
ALT+0192 |
à |
ALT+133 |
|
|
Á |
ALT+0193 |
á |
ALT+160 |
|
|
 |
ALT+0194 |
â |
ALT+131 |
|
|
Ç |
ALT+128 |
ç |
ALT+135 |
|
|
Č |
010C+ALT+X |
č |
010D+ALT+X |
|
|
É |
ALT+144 |
é |
ALT+130 |
|
|
È |
ALT+0200 |
è |
ALT+138 |
|
|
Ê |
ALT+202 |
ê |
ALT+136 |
|
|
Ë |
ALT+203 |
ë |
ALT+137 |
|
|
Ĕ |
0114+ALT+X |
ĕ |
0115+ALT+X |
|
|
Ğ |
011E+ALT+X |
ğ |
011F+ALT+X |
|
|
Ģ |
0122+ALT+X |
ģ |
0123+ALT+X |
|
|
Ï |
ALT+0207 |
ï |
ALT+139 |
|
|
Î |
ALT+0206 |
î |
ALT+140 |
|
|
Í |
ALT+0205 |
í |
ALT+161 |
|
|
Ì |
ALT+0204 |
ì |
ALT+141 |
|
|
Ñ |
ALT+165 |
ñ |
ALT+164 |
|
|
Ö |
ALT+153 |
ö |
ALT+148 |
|
|
Ô |
ALT+212 |
ô |
ALT+147 |
|
|
Ō |
014C+ALT+X |
ō |
014D+ALT+X |
|
|
Ò |
ALT+0210 |
ò |
ALT+149 |
|
|
Ó |
ALT+0211 |
ó |
ALT+162 |
|
|
Ø |
ALT+0216 |
ø |
00F8+ALT+X |
|
|
Ŝ |
015C+ALT+X |
ŝ |
015D+ALT+X |
|
|
Ş |
015E+ALT+X |
ş |
015F+ALT+X |
|
|
Ü |
ALT+154 |
ü |
ALT+129 |
|
|
Ū |
ALT+016A |
ū |
016B+ALT+X |
|
|
Û |
ALT+0219 |
û |
ALT+150 |
|
|
Ù |
ALT+0217 |
ù |
ALT+151 |
|
|
Ú |
00DA+ALT+X |
ú |
ALT+163 |
|
|
Ÿ |
0159+ALT+X |
ÿ |
ALT+152 |
К началу страницы
Коды часто используемых лигатур
Дополнительные сведения о лигатурах см.
в статье Лигатура (соединение букв). Полный список лигатур и соответствующих кодов см. в таблице символов.
|
Глиф |
Код |
Глиф |
Код |
|
|---|---|---|---|---|
|
Æ |
ALT+0198 |
æ |
ALT+0230 |
|
|
ß |
ALT+0223 |
ß |
ALT+225 |
|
|
Π|
ALT+0140 |
œ |
ALT+0156 |
|
|
ʩ |
02A9+ALT+X |
|||
|
ʣ |
02A3+ALT+X |
ʥ |
02A5+ALT+X |
|
|
ʪ |
02AA+ALT+X |
ʫ |
02AB+ALT+X |
|
|
ʦ |
0246+ALT+X |
ʧ |
02A7+ALT+X |
|
|
Љ |
0409+ALT+X |
Ю |
042E+ALT+X |
|
|
Њ |
040A+ALT+X |
Ѿ |
047E+ALT+x |
|
|
Ы |
042B+ALT+X |
Ѩ |
0468+ALT+X |
|
|
Ѭ |
049C+ALT+X |
ﷲ |
FDF2+ALT+X |
К началу страницы
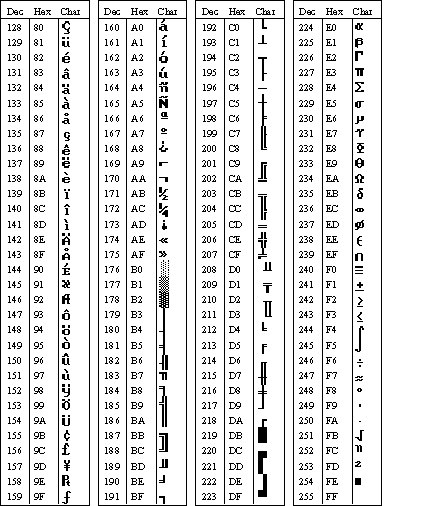
Непечатаемые управляющие знаки ASCII
Знаки, используемые для управления некоторыми периферийными устройствами, например принтерами, в таблице ASCII имеют номера 0–31.
Например, знаку перевода страницы/новой страницы соответствует номер 12. Этот знак указывает принтеру перейти к началу следующей страницы.
Таблица непечатаемых управляющих знаков ASCII
|
Десятичное число |
Знак |
Десятичное число |
Знак |
|
|---|---|---|---|---|
|
NULL |
0 |
Освобождение канала данных |
16 |
|
|
Начало заголовка |
1 |
Первый код управления устройством |
17 |
|
|
Начало текста |
2 |
Второй код управления устройством |
18 |
|
|
Конец текста |
3 |
Третий код управления устройством |
19 |
|
|
Конец передачи |
4 |
Четвертый код управления устройством |
20 |
|
|
Запрос |
5 |
Отрицательное подтверждение |
21 |
|
|
Подтверждение |
6 |
Синхронный режим передачи |
22 |
|
|
Звуковой сигнал |
7 |
Конец блока передаваемых данных |
23 |
|
|
BACKSPACE |
8 |
Отмена |
24 |
|
|
Горизонтальная табуляция |
9 |
Конец носителя |
25 |
|
|
Перевод строки/новая строка |
10 |
Символ замены |
26 |
|
|
Вертикальная табуляция |
11 |
ESC |
27 |
|
|
Перевод страницы/новая страница |
12 |
Разделитель файлов |
28 |
|
|
Возврат каретки |
13 |
Разделитель групп |
29 |
|
|
Сдвиг без сохранения разрядов |
14 |
Разделитель записей |
30 |
|
|
Сдвиг с сохранением разрядов |
15 |
Разделитель данных |
31 |
|
|
Пробел |
32 |
DEL |
127 |
К началу страницы
Таблица символов цифр: арабские, римские, греческие, иврит
В таблице ниже представлены числа от 1 до 100, записанные цифрами разных систем счислений: арабской, римской, греческой, индо-арабской и еврейской.
| Название числа | Арабские цифры | Римские цифры | Греческие цифры | Индо-арабские цифры | Цифры на иврите |
| ноль | 0 | ٠ | |||
| один | 1 | I | α | ١ | א |
| два | 2 | II | β | ٢ | ב |
| три | 3 | III | γ | ٣ | ג |
| четыре | 4 | IV | δ | ٤ | ד |
| пять | 5 | V | ε | ٥ | ה |
| шесть | 6 | VI | ϝ или ϛ | ٦ | ו |
| семь | 7 | VII | ζ | ٧ | ז |
| восемь | 8 | VIII | η | ٨ | ח |
| девять | 9 | IX | θ | ٩ | ט |
| десять | 10 | X | ι | ١٠ | י |
| одиннадцать | 11 | XI | ια | ١١ | יא |
| двенадцать | 12 | XII | ιβ | ١٢ | יב |
| тринадцать | 13 | XIII | ιγ | ١٣ | יג |
| четырнадцать | 14 | XIV | ιδ | ١٤ | יד |
| пятнадцать | 15 | XV | ιε | ١٥ | טו |
| шестнадцать | 16 | XVI | ιϛ | ١٦ | טז |
| семнадцать | 17 | XVII | ιζ | ١٧ | יז |
| восемнадцать | 18 | XVIII | ιη | ١٨ | יח |
| девятнадцать | 19 | XIX | ιθ | ١٩ | יט |
| двадцать | 20 | XX | κ | ٢٠ | כ |
| тридцать | 30 | XXX | λ | ٣٠ | ל |
| сорок | 40 | XL | μ | ٤٠ | מ |
| пятьдесят | 50 | L | ν | ٥٠ | נ |
| шестьдесят | 60 | LX | ξ | ٦٠ | ס |
| семьдесят | 70 | LXX | ο | ٧٠ | ע |
| восемьдесят | 80 | LXXX | π | ٨٠ | פ |
| девяносто | 90 | XC | ϟ | ٩٠ | צ |
| сто | 100 | C | ρ | ١٠٠ | ק |
microexcel.
_` { | } ~ (33 символа)
Имя пользователя для входа в систему
Пробелы, двоеточия и кавычки не допускаются.
Оно не может состоять только из цифр, и поле нельзя оставлять незаполненным.
Длина ограничивается 32 символами.
Пароль для входа в систему
Максимально допустимая длина пароля для администраторов и супервайзера составляет 32 символа, тогда как для пользователей длина ограничивается 128 символами.
В отношении типов символов, которые могут использоваться для задания пароля, никаких ограничений не установлено. В целях безопасности рекомендуется создавать пароли, содержащие буквы верхнего и нижнего регистров, цифры и другие символы. Чем большее число символов используется в пароле, тем более трудной является задача его подбора для посторонних лиц.
В подразделе [Политика паролей] раздела [Расширенная безопасность] вы можете установить требование в отношении обязательного включения в пароль букв верхнего и нижнего регистров, цифр и других символов, а также минимально необходимое количество символов в пароле.
Для получения сведений об определении политики паролей см. Настройка функций расширенной безопасности.
Для получения сведений об определении политики паролей см. Настройка функций расширенной безопасности.Цифры, цифры и цифры
Номер
Число — это счетчик или измерение, которое на самом деле является идеей в нашем сознании.
Мы пишем или говорим о числах, используя цифр , таких как «4» или «четыре».
Но мы также можем поднять 4 пальца или 4 раза постучать по земле.
Это разные способы обозначения одного и того же номера.
Существуют также специальные числа (например, π (Пи)), которые нельзя записать точно, но они по-прежнему являются числами, потому что мы знаем, что за ними стоит идея .
Цифра
Цифра — это символ или имя , обозначающее число.
Примеры: 3 , 49 и двенадцать — все числа.
Итак, число — это идея, цифра — это то, как мы его записываем.
цифра
Цифра — это единичный символ , используемый для составления цифр.
0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — это десять цифр, которые мы используем в повседневных числах.
Пример: цифра 153 состоит из 3 цифр («1», «5» и «3»).
Пример: цифра 46 состоит из 2 цифр («4» и «6»).
Пример: цифра 9 состоит из 1 цифры («9»). Таким образом, одна цифра также может быть цифрой
.Мы можем использовать и другие символы, например, в шестнадцатеричном формате также используются некоторые буквы!
Цифры -> Цифры -> Цифры
Таким образом, цифры составляют цифры, а цифры обозначают идею числа.
Также как буквы составляют слова, а слова выражают идею предмета.
Номер вместо цифры
Но часто люди (в том числе и я) говорят «Число», хотя им действительно следует сказать «Числовое» … неважно, если вы это сделаете, потому что другие люди вас понимают.
Но попробуйте использовать «цифру» только когда говорите об отдельных символах, составляющих цифры, хорошо?
Цифры и цифры других типов
Мы все привыкли использовать такие числа, как «237» и «99», но римляне использовали римские цифры, и на протяжении всей истории использовалось много других цифр и цифр.
цифр, символов и знаков препинания на английском языке
Следуйте списку;
Список кардинальных, порядковых и римских цифр;
| Кардинальные числа | Порядковые номераримские цифры | |
|---|---|---|
| 1 — один | 1-я — первая | 1 — Я |
| 2 — два | 2-я — вторая | 2 — II |
| 3 — три | 3-й — 3-й | 3 — III |
| 4 — четыре | 4-я — 4-я | 4 — IV |
| 5-5 | 5–5 | 5 — В |
| 6 — шесть | шестой — шестой | 6 — VI |
| 7-7 | 7-7 | 7 — VII |
| 8-8 | 8-8 | 8 — VIII |
| 9 — девять | 9-9 | 9 — IX |
| 10 — десять | 10–10 | 10 — Х |
| 11 — одиннадцать | 11-11-е | 11 — XI |
| 12 — двенадцать | 12–12 | 12 — XII |
| 13 — тринадцать | 13–13 | 13 — XIII |
| 14 — четырнадцать | 14–14 | 14 — XIV |
| 15 — пятнадцать | 15-15 | 15 — XV |
| 16 — шестнадцать | 16–16 | 16 — XVI |
| 17 — семнадцать | 17 — семнадцатая | 17 — XVII |
| 18–18 лет | 18-18-е | 18 — XVIII |
| 19 — девятнадцать | девятнадцатое — девятнадцатое | 19 — XIX |
| 20 — двадцать | 20-20-е | 20 — ХХ |
| 21 — двадцать один | 21 — двадцать первое | 21 — XXI |
| 30–30 лет | 30–30 | 30 — ХХХ |
| 40 — четыре года | 40-40 | 40 — XL |
| 50 — пятьдесят | 50-50 | 50 — L |
| 60 — шестьдесят | 60-60 | 60 — LX |
| 70 — семьдесят | 70 — семидесятые | 70 — LXX |
| 80 — восемьдесят | 80-80-е | 80 — LXXX |
| 90 — девяносто | 90 — девяностые | 90 — ХС |
| 100 — сто | сотые — сотые | 100 — С |
| 500 — пятьсот | 500-5 сотых | 500 — Д |
| 1000 — одна тысяча | 1000-я — одна тысячная | 1000 — M |
Список символов и знаков препинания;
| Обозначение | Значение | Символ | Значение |
| + | плюс | – | минус |
| х | умножить на | ÷ | делить на |
| = | равно | > | больше |
| < | менее | % | процентов |
| и | и | @ | при |
| ° | градусов | √ | корень квадратный |
| π | пи | $ | доллар |
| © | авторское право | . | полная остановка |
| , | запятая | ; | точка с запятой |
| : | толстая кишка | ? | вопросительный знак |
| ! | восклицательный знак | – | тире |
| * | звездочка | () | скобки |
| «» | кавычки | ‘ | апостроф |
Как сравнивать числа с математическими символами — Видео и стенограмма урока
Больше
Первый символ, который мы обсудим, — это символ больше .Этот символ выглядит так:>. Большее число идет с левой стороны. Если вы посмотрите на символ, вы увидите, что одна сторона больше, чем другая. Если большая сторона обращена влево, значит, вы смотрите на символ «больше». Чтобы использовать его для сравнения двух чисел, мы пишем наше большее число слева, например: 10> 8.
Меньше
Нашим следующим символом является символ меньше .
Этот символ выглядит так: <. Меньшее число идет с левой стороны.Посмотрев на этот символ, вы увидите, что теперь большая сторона обращена вправо, а меньшая сторона обращена влево. Чтобы использовать этот символ, мы пишем меньшее число слева, например: 8 <10.
Equal To
Третий и последний символ, который мы обсуждаем в этом уроке, — это , равный . Этот символ сообщает вам, когда два числа равны друг другу. Выглядит это так: =. Вы будете использовать этот символ, когда числа на обеих сторонах одинаковы, например: 10 = 10.
Примеры
Я использовал всего пару чисел, чтобы показать вам, как работают символы. Эти символы можно использовать с любыми двумя числами, и вы встретите их в тестах по математике. У вас может возникнуть проблема с просьбой записать правильный символ, чтобы показать взаимосвязь между двумя числами. Например, вы можете столкнуться с такой проблемой, когда вас попросят ввести правильный символ в поле между двумя числами:
Вы смотрите на два числа и должны решить, больше ли число слева, меньше или равно числу справа.
Глядя на эти два числа, вы видите, что число слева меньше числа справа, поэтому правильным символом для вставки в поле является символ меньше <.
Что с этой проблемой?
Какой символ помещен в эту рамку?
Глядя на свои числа, вы видите, что число слева, 76, больше, чем число справа, 67. Итак, правильный символ, который стоит в рамке, — это символ больше>.
Итоги урока
Давайте рассмотрим, что мы узнали. Для сравнения двух чисел можно использовать символ больше , символ меньше или равен . Вот краткое описание символов, включая их внешний вид и примеры их использования:
| Имя | Символ | Пример |
|---|---|---|
| Больше | > | 10> 8 |
| Менее | < | 8 <10 |
| Равно | = | 10 = 10 |
Результат обучения
После завершения этого урока учащиеся должны уметь уверенно распознавать математические символы, используемые для сравнения чисел и решать случайные примеры каждого из них.
английских символов и цифр
английских символов и цифрСимвол | Значение |
|---|---|
| и | и |
| ~ | приблизительно / об / более или менее |
| @ | при |
| ° | градус |
| $ | Доллар |
| = | равно / совпадает с |
| € | Евро |
| > | больше / лучше / больше |
| ∞ | бесконечность |
| < | меньше / меньше |
| – | минус |
| # | номер |
| ¶ | пункт |
| % | процента |
| + | plus, в дополнение к |
| £ | фунтов |
| § | раздел |
| \ | следовательно |
| ¥ | Йена |
| 2D | Двумерный |
| 3D | Трехмерный |
| 3G | Третье поколение (технология мобильных телефонов) |
| 4D | Четырехмерный |
| 4WD | Полный привод |
24/7 | 24 часа в сутки, 7 дней в неделю |
404 | Не знаю ^ |
 w3.org/1999/xhtml» cellspacing=»0″> | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Следующие символы используются для форматирования чисел.Утвержденные символы для локали будут заменены заполнителями, описанными в Шаблоны номеров. Для английских региональных стандартов (например, en_DE), где английский не является основным языком страны / региона (например, en_DE; английский, используемый в Германии), числовые форматы и форматы даты должны соответствовать английскому форматированию, используемому в этой стране. /область, край. Часто использование форматирования на английском языке, как правило, соответствует британскому или американскому форматированию, а не форматированию основного языка.Проконсультируйтесь с английскими версиями известных журналов или газет по поводу использования даты и числового формата.
💡 Полезные советы
|
Например, в операции 3 — (- 2) определенный символ будет использоваться для второго знака минус, но не для оператора вычитания. Любые маркеры направления (например, 
Написание слов и символов
Предварительные знания.
- Сложение, вычитание, умножение и деление целых чисел, а также задачи записи слов с помощью символов
- Объясните: букву можно использовать для обозначения «некоторого числа», которое нам не обязательно знать.
Упражнения в этом упражнении различаются по сложности от EA до AP.Учителю нужно будет выбрать наиболее подходящие для своих учеников.
Фон
Эти упражнения направлены на развитие понимания языка математики. Они включают в себя развитие понимания соглашений, которые мы используем для записи фраз на этом языке, и интерпретацию того, что эти фразы означают.
Комментарии к упражнениям
Упражнение 1
Попросите студентов написать фразы, используя символы вместо слов. В этом упражнении не предполагается, что учащиеся знакомятся со всеми алгебраическими условностями.
Это упражнение можно проделать дважды. Вначале полезно развить идею о том, что буква n (обратите внимание на курсив) используется для обозначения «некоторого числа» (см. Прилагаемое учебное задание «алфавитный суп»). Затем учащиеся могут продолжить выполнение упражнения, просто используя это понимание. Полезное продолжение — задать вопрос: «Есть ли причина, по которой нам пришлось использовать букву n ? Пока мы понимаем, что говорим о «некотором числе», можем ли мы использовать другую букву (которую мы хотели использовать? »). Затем обсуждение может привести к мысли, что в некоторых ситуациях мы используем n (например, с шаблонами ), иногда x (с графиками и функциями), иногда a и т. д.Затем упражнение можно сбросить, при этом учащиеся будут использовать разные буквы в разных задачах для обозначения «некоторого числа».
Обратите внимание, что учебное задание «Алфавитный суп» знакомит с обозначениями символов, которые студенты должны знать, чтобы записывать символьные фразы для числовых задач, выраженные словами (например, записывая «половину шести» как «1/2 x 6»).
Надлежащая запись таких фраз и эквивалентность записанных по-разному фраз должна быть рассмотрена в числовом контексте перед использованием этого упражнения.
Упражнение 2
Попросите учащихся написать фразы, используя символы. Для этого упражнения ученики должны показать два числа , используя символы. Это может быть намного сложнее, чем работать с одним символом отдельно, поэтому перед тем, как приступить к выполнению упражнения, необходимо обсудить, как это сделать. Скажите студентам: «Вы научились использовать букву для обозначения некоторого числа, с которым вы хотите работать. Как ты думаешь, ты записываешь, что хочешь сложить два разных числа? » Это должно натолкнуть на мысль, что в одном предложении должны использоваться две разные буквы.(Это могут быть a и b или n и r …). Затем ученики должны попрактиковаться с некоторыми простыми задачами, устно выраженными словами, которые они записывают с помощью символов.
Некоторым студентам сначала может потребоваться использовать одни и те же буквы для всех вопросов, в то время как другим будет удобно менять буквы, которые они используют для каждой задачи. Отмечая эти устные вопросы, обсуждение того, какие буквы использовали люди, может быть ценным способом снова подчеркнуть, что не имеет значения, какие буквы выбраны для вопроса, если они были разными.
Идея о том, что даже когда мы используем две разные буквы, у нас есть особый случай (соглашение), что два числа могут фактически быть одинаковыми, должна быть представлена на этом этапе. Полезный способ сделать это — спросить, что означает это предложение:
x + y = 12
, а затем «какие числа мы можем использовать, чтобы сделать это правдой?»
В этом упражнении возникает необходимость в скобках для группировки и разделения чисел. Учащиеся могут быть готовы к этому дополнительному соглашению, а могут и не быть, поэтому в упражнении 3 об этом будет сказано больше.
Упражнение 3
Предлагает студентам посмотреть, как используются скобки в числовых задачах. Имеет смысл установить упражнение без предварительного обучения, так как есть примечание о правилах использования скобок в математике над упражнением. (Возможно, стоит обсудить, что такое соглашение, если этот термин не соблюдался раньше.)
Вопрос о том, чтобы не менять порядок написания вещей, исследуется в вопросе 9. Вопрос структурирован таким образом, что, отвечая на вопросы, учащиеся могут понять, что не все они написали одно и то же (некоторые могут даже понять что будет отрицательный ответ, если порядок будет изменен на 9а).Этот вопрос был предоставлен, чтобы дать возможность обсудить условные обозначения, которые математики используют в этой области, поскольку студенты, вероятно, привнесут в эту работу ряд важных заблуждений, которые необходимо устранить, если обучение будет иметь место.
После этого обсуждения ученикам может быть уместно вернуться к упражнениям 2 и 3 в контексте их нового изучения.
Упражнение 4
Попросите учащихся объяснить, что фразы с символами говорят о том, что они делают с числами.Некоторые вопросы в этом упражнении (например, n /2 в вопросе 8) могут быть немного незнакомы учащимся, хотя учащимся следует попробовать их все без строительных лесов. При настройке упражнения предложите студентам написать, что, по их мнению, означает эта фраза, даже если они не уверены. (Помещение звездочки рядом с ответами, в которых они не уверены, является хорошей практикой и позволит учащимся определить, на что им нужно обратить особое внимание во время обсуждения во время выставления оценок).
Важно отметить это упражнение коллективно, так как разные словосочетания, написанные учащимися, могут означать одно и то же.(Это может привести к пересмотру языка, используемого для обозначения использования различных операций.) Затем можно обсудить обозначения, подобные тем, которые используются в вопросах 6, 7, 8, 9, 12, 20, 22 и 23, а также стандартные интерпретации введен.
Полезным продолжением этого упражнения является учебное занятие, на котором учитель записывает на доске серию утверждений по алгебре, и учащиеся в парах обсуждают то, что, по их мнению, они имеют в виду, прежде чем поделиться своим мнением с группой.
Задание в паре
Это задание задумано как мышление и основано на работе, проделанной при выставлении оценок за упражнение 3.Студентам это может показаться трудным, но им следует разрешить работать над задачей без каких-либо строительных лесов или вмешательства. Им нужно подумать о том, как записать эти проблемы, прежде чем обсуждать «ответы» с учителем. Цель упражнения — научить учащихся осознать, что то, как мы записываем такие проблемы, является условным. Если повезет, некоторые группы могут «решить» задачу и придумать аналогичные способы записи проблем, в то время как другие придумают другой подход. Это позволит обсудить необходимость последовательного подхода, чтобы у всех было одинаковое понимание того, что имеется в виду.
В этом процессе учащиеся также должны развивать идею о том, что «буквы», будучи числами (хотя и неизвестными), подчиняются основным правилам, которые действуют в отношении чисел, что является важной идеей для дальнейшего изучения.
Хорошим продолжением задания в паре будет задание учеников написать рабочий лист для других учеников. По этому поводу они должны объяснить, как у нас есть соглашения о записи умножения и деления, когда мы используем буквы, и как они работают. Затем они должны составить несколько упражнений для студентов, над которыми они будут практиковаться, — конечно, с ответами.Затем учащиеся должны обменяться работой с кем-нибудь еще, чтобы проверить, имеет ли она смысл и правильность ответов.
Упражнение 5
Просит студентов использовать правила записи умножения и деления при использовании символов вместо слов во фразах. Это упражнение основано на задаче и знакомит с использованием закона коммутативности, чтобы убедиться, что умножения с использованием букв можно записать так, чтобы они выглядели одинаково.
Также рассматривается использование обозначения дробей для записи делений.Некоторые вопросы также требуют, чтобы студенты использовали скобки, чтобы убедиться, что операции выполняются в правильном порядке.
Учащимся можно предложить написать собственное упражнение с ответами. «Затем можно поменять местами лучшие вопросы и создать новый рабочий лист для использования в следующем году.
Упражнение 6
Попросите студентов записать словами, о чем вас просят сделать условные фразы.
Это упражнение позволяет лучше понять язык символов и является довольно продвинутым.Здесь используются скобки (следовательно, порядок операций) и понимание того, какая работа скобок в выражении ожидается. В некоторых вопросах также вводятся ситуации, когда другие символы означают, что скобки не нужны. Это упражнение, возможно, потребуется тщательно обсудить после его завершения.
Вопрос 19 снова побуждает студентов написать и попробовать свои собственные задачи.
Это хорошее занятие, которым можно поделиться во время учебного занятия, чтобы учащиеся могли написать выражение, а другие могли записать, что, по их мнению, оно должно делать с числами.Здесь можно исправить любые оставшиеся заблуждения.
Упражнение 7
Попросите учащихся интерпретировать фразы, содержащие, например, 2n, и показать их на числовой прямой. В этом упражнении используется контекст измерения для изучения относительного размера чисел. Студенты должны понимать, что в этой модели длина (и расстояние от нуля) передают смысл. Например, 2 n должно быть вдвое больше расстояния от нуля, чем n , а при размещении n + 1 он идет справа от n, и размещение этого определяет длину единицы (так что один раз размещенный n — 1 необходимо разместить на равном расстоянии от n , но слева от него).Это действительно может позволить вам определить, какое число n находится на числовой строке…
Более поздние задачи помещают в , так что это отрицательное число, а затем как десятичное (или дробное), что имеет последствия для различных других чисел.
Это упражнение стоит обсудить во время учебного занятия, хотя снова позвольте студентам попробовать его до того, как это обсуждение будет проведено.
Цифры в Юникоде ① ② ③
Автор Xah Lee. Дата: .Последнее обновление: .
Номер в белом обведении
⓪ ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ 911 11 11 11 11 11 911 911 1133 911 911 ⑰ ⑱ ⑲ ⑳ ㉑ ㉒ ㉓ ㉔ ㉕ ㉖ ㉗ 11 1133 911 911 911 911 911 911 911 ㉝ ㉞ ㉟ ㊱ ㊲ ㊳ ㊴ ㊵ ㊶ ㊷ ㊸ ㊹ 912 11 912 911 ㊿
Это, в частности, без засечек: ⓿ ❶ ❷ ❸ ❹ ❺ ❻ ❼ ❽ ❾ ❿ ⓫ ⓬ ⓭ ⓮ ⓯ ⓰ ⓱ ⓲ ⓳ ⓴ Это, в частности, без засечек: НА ЧЕРНОЙ ПЛОЩАДИ ⓵ ⓶ ⓷ ⓸ ⓹ ⓺ ⓻ ⓼ ⓽ ⓾ 🄀 ⒈ ⒉ ⒊ ⒋ ⒌ ⒍ ⒎ ⒏ ⒐ 40 911 1133
🄋 ➀ ➁ ➂ ➃ ➄ ➅ ➆ ➇ ➈ 33 3 Номер в черном обведении
🄌 ➊ ➋ ➌ ➍ ➎ ➏ ➐ ➑ ➒ 33 ➓3
㉈ ㉉ ㉊ ㉋ ㉌ ㉍ ㉎ ㉏ Двукратный номер
Число с периодом
Число в скобках
⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽ ⑾ 933 11 911 911 911 911 911 911 ⒅ ⒇
Номер в китайском кружке
㊀ ㊁ ㊂ ㊃ ㊄ ㊅ ㊆ ㊇ ㊈ ㊉
Письмо с круглыми скобками
🄐 🄑 🄒 🄓 🄔 🄕 🄖 🄗 🄘 🄙 🄚33 🄚33 915 911 911 911 911 911 911 911 911 911 911 911 911 911 911 🄡 🄢 🄣 🄤 🄥 🄦 🄧 🄨 🄩
⒜ ⒝ ⒞ ⒟ ⒠ ⒡ ⒢ ⒣ ⒤ ⒥ ⒦33 1133 ⒦33 915 911 1133 911 11 911 911 911 911 911 ⒭ ⒮ ⒯ ⒰ ⒱ ⒲ ⒳ ⒴ ⒵
Буквы в белых кружках
Ⓐ Ⓑ Ⓒ Ⓓ Ⓔ Ⓕ Ⓖ Ⓗ Ⓘ Ⓙ Ⓚ33 911 33 1133 911 1133 911 1133 911 Ⓡ Ⓢ Ⓣ Ⓤ Ⓥ Ⓦ Ⓧ Ⓨ Ⓩ
ⓐ ⓑ ⓒ ⓓ ⓔ ⓕ ⓖ ⓗ ⓘ ⓙ ⓚ 16 911 33 11 11 11 911 911 911 911 911 ⓡ ⓢ ⓣ ⓤ ⓥ ⓦ ⓧ ⓨ ⓩ
Буквы в черном кружке
🅐 🅑 🅒 🅓 🅔 🅕 🅖 🅗 🅘 🅙 🅚33 11 911 3311 911 911 911 911 911 911 911 911 🅡 🅢 🅣 🅤 🅥 🅦 🅧 🅨 🅩
Квадратные буквы
🄰 🄱 🄲 🄳 🄴 🄵 🄶 🄷 🄸 🄹 🄺 911 911 911 911 911 911 911 911 911 911 🅁 🅂 🅃 🅄 🅅 🅆 🅇 🅈 🅉
🅰 🅱 🅲 🅳 🅴 🅵 🅶 🅷 🅸 🅹 🅺33 911 1133 911 11 11 911 1133 911 911 11 🆁 🆂 🆃 🆄 🆅 🆆 🆇 🆈 🆉
Вот скриншот того, как они выглядят.