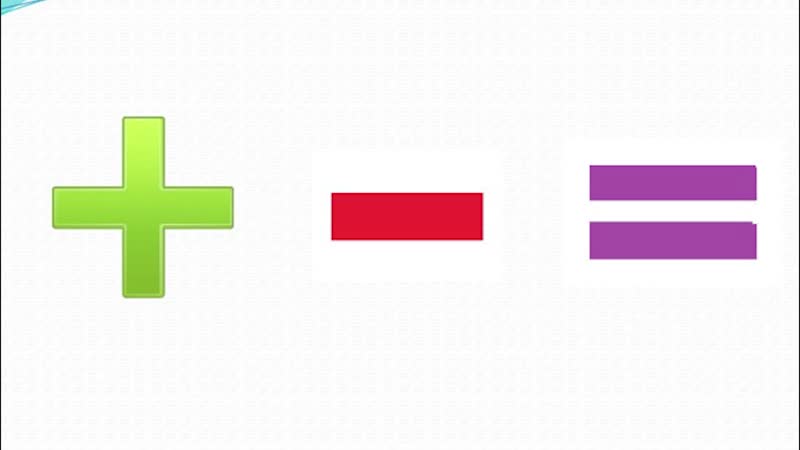на клавиатуре, в окне программы
На компьютерной клавиатуре, помимо букв алфавита и цифр, также представлены самые популярные символы, которые чаще всего используются в программах при работе с текстовой и другой информацией, в том числе, знаки сравнения – “больше” и “меньше”. Но что делать, если требуется вставить символ “не равно”, который физически не представлен на устройстве ввода? Давайте посмотрим, как можно справиться с этой задачей в Эксель.
Примечание: В Excel “не равно” используется в двух вариантах:
- “<>” – в формулах и функциях;
- “≠” – для визуализации информации.
Знак “<>”
Данный знак используется для задания логического условия в формулах и аргументах функций. Также некоторые пользователи даже при визуальном отображении информации предпочитают использовать этот символ вместо “≠”.
Т.к. оба символа (“<“ и “>”), из которых состоит знак, представлены на клавиатуре, все что требуется, чтобы напечатать их – нажать соответствующие клавиши вместе с зажатым  Обратите внимание на раскладку клавиатуры (должна быть английская), в случае неверного выбора будут напечатаны заглавные буквы “Б” и “Ю”.
Обратите внимание на раскладку клавиатуры (должна быть английская), в случае неверного выбора будут напечатаны заглавные буквы “Б” и “Ю”.
Если вдруг клавиатура перестала работать (например, сели батарейки), и срочно требуется набрать знак, можно выполнить следующие действия:
- Встаем в ячейку, в которую хотим вставить символ. Переключаемся во вкладку “Вставка” и щелкаем по пункту “Символы” в левом углу ленты программы. В раскрывшемся перечне выбираем
- На экране отобразится окно, через которое мы можем добавить в документ всевозможные знаки, в том числе, не вынесенные на клавиатуру. Для удобства поиска раскрываем список доступных вариантов для параметра “Набор” и останавливаемся на “Основной латинице”. Щелкаем по знаку “<“, затем – по кнопке “Вставить”. Аналогичным образом вставляем “>”. По готовности закрываем окно.
Примечание: данный метод подходит в исключительных случаях, когда необходимо внести единичные правки в документ, т. к. для полноценной работы с информацией нужна рабочая клавиатура (хотя бы виртуальная).
к. для полноценной работы с информацией нужна рабочая клавиатура (хотя бы виртуальная).
Символ “≠”
Этот символ в виде перечеркнутого знака “равно” предназначен только красивого визуального оформления информации. Он не воспринимается программой как математический, следовательно, в формулах применяться не может.
Т.к. знак не представлен на клавиатуре, его можно найти и вставить только через специальное окно, которое мы рассмотрели выше.
Для параметра “Набор” выбираем вариант – “Математические операторы”. Выбираем знак щелчком мыши, жмем кнопку “Вставить”, после чего закрываем окно.
Заключение
Таким образом, в том, чтобы поставить знак “не равно” в Эксель, нет ничего сложного. Для начала нужно определиться с его значением – математическое или визуальное. В первом случае используется комбинация знаков “меньше” и “больше”, во втором – символ в виде перечеркнутого знака “равно”.
Как вставить знак «не равно» в Excel
Программный продукт от Microsoft под названием Excel чаще всего используется для работы с электронными таблицами, проведения вычислений и подсчетов, построения диаграмм и графиков, а также имеет еще массу полезных свойств. Умение пользоваться инструментами Excel значительно облегчает работу бухгалтеров, финансистов, статистов и представителей других отраслей.
Умение пользоваться инструментами Excel значительно облегчает работу бухгалтеров, финансистов, статистов и представителей других отраслей.
Где используется знак «не равно»
Знак «не равно» (≠) используется в функции «СУММЕСЛИ», которая позволяет производить суммирование не всех данных, а только ряда цифр, соответствующих логическим условиям.
Функция «=СУММЕСЛИ»Указанная функция работает с учетом нескольких аргументов:
- Диапазон – оценка ячеек определенным критериям.
- Критерий – выбор ячеек в соответствии с диапазоном.
- Суммирующий диапазон – суммирование ячеек, удовлетворяющих поставленным условиям.
В некоторых случаях допускается исключение последнего аргумента, но критерий и диапазон продолжают функционировать.
Пример применения функции «=СУММЕСЛИ»Обратите внимание! Последовательность знаков «<» и «>» очень важна. Если последовательность нарушена – функция не работает.
Ставим знак «не равно» с клавиатуры
Символ «не равно» можно поставить в ячейку несколькими способами:
- с помощью клавиатуры;
- используя специальные символы.

Среди множества клавиш на клавиатуре нет кнопки с символом ≠, но для проведения вычислений в программе Excel она и не используется. Чтобы соответствующая функция сработала, вместо «не равно» следует набрать на клавиатуре знаки «<» (меньше) и «>» (больше). Причем делается это в английской раскладке и с зажатой клавишей Shift.
Если не соблюсти все указанные требования, то в активной ячейке появятся значения «Б» и «Ю», которые не несут в себе абсолютно никакого математического значения, и функция не будет выполнена. Должно получиться сочетание символов «<>», которое соответствует значению «не равно». Символ «≠» не работает как математический знак, он имеет исключительно визуальное значение. Также не стоит забывать о существовании специальных комбинаций Alt-кодов, которые позволяют ввести с клавиатуры практически любой символ. Таким образом знак «≠» с компьютерной клавиатуры можно ввести, воспользовавшись комбинацией клавиш Alt+8800.
Совет! Набор Alt-кодов работает только с цифровыми клавишами в правой части клавиатуры и с активированной функцией NumLock.
Другие варианты поставить знак «не равно»
В некоторых случаях использование клавиатуры может быть недоступным: села батарейка на устройстве с Bluetooth-подключением или работа осуществляется с планшета или мобильного телефона. В любом случае, выбор метода ввода специальных символов остается за пользователем.
Вкладка «Символы» в ExcelТак, одним из способов введения знака «не равно» является использование библиотеки специальных символов:
- Во вкладке «Вставить» есть блок «Символы», в котором следует выбрать кнопку «Символ».
- Как правило, знак «≠» можно найти среди наиболее популярных. В противном случае, вызываем меню «Другие символы».
- Для быстрого поиска в параметре «Набор» нужно выбрать категорию «Математические операторы».
Кстати, во вкладке «Символы» также присутствуют и необходимые для осуществления соответствующих вычислений символы «<» и «>». Но их следует искать в категории «Основная латиница».
Но их следует искать в категории «Основная латиница».
Введение символов активируется нажатием на выбранный символ и кнопкой «Вставить» в этой же вкладке «Символы». После достижения цели, то есть появления необходимых символов в активной ячейке, окно «Специальные символы» можно закрыть.
Справка! Вкладка «Символы» предлагает на выбор не только специальные математические символы, но и товарные знаки, обозначения денежных единиц, символы авторского права.
Какой способ лучше использовать
Пользователи программы Excel для написания вычислительных формул и функций чаще используют клавиатуру. Этот метод одновременно быстрый и удобный. А вариант с вызовом вкладки «Символы» может использоваться для однократного редактирования документа или в других исключительных случаях. Для визуального оформления документа с использованием символа «не равно», другого способа введения знака «≠» не существует, кроме как выбором из предложенной библиотеки символов.
Оцените качество статьи. Нам важно ваше мнение:
Java. Экспресс-курс: Операторы сравнения
Статья проплачена кошками — всемирно известными производителями котят.
Операторы сравнения выдают логический результат (boolean). Если условие проверки истинно, оператор выдает true, а если ложно — false. К операторам сравнения относятся < (меньше чем), > (больше чем), <= (меньше чем или равно), >= (больше чем или равно), == (равно), != (не равно). Операторы «Равно» и «не равно» можно использовать для всех примитивных типов данных, однако остальные сравнения нельзя использовать к типу boolean.![]() b
b
Наиболее часто операции сравнения используют в выражениях, которые управляют оператором if и операторами цикла.
Обратите внимание, что равенство обозначается двумя знаками равно (==), одиночный знак равно (=) — это оператор присваивания. Типичная ошибка начинающих программистов.
Корректный вариант примера:
int x = 5;
int y = 7;
boolean z = a < b; // результат сохраняется в переменной типа boolean
Примеры для оператора if для Java (В C++ используется другой синтаксис!):
int cat_age;
if(cat_age == 4) // нельзя if(cat_age) - нет сравнения
if(cat_age != 9) // нельзя if(!cat_age) - нет сравнения
Помните, что в Java значения true и false не являются числовыми значениями, как в C++, поэтому, чтобы сравнить значение с другим значением, необходимо явно использовать операторы сравнения.
Реклама
Операторы сравнения — JavaScript | MDN
В JavaScript имеются как строгие сравнения, так и сравнения с преобразованием типа операндов. Строгие сравнения (к примеру, ===) истинны только в том случае, если типы сравниваемых значений являются одинаковыми (к примеру: string-string, number-number). Однако, чаще используются сравнения с преобразованием типов (к примеру, ==). Такой тип сравнения, перед тем как непосредственно выполнить сравнение, приводит операнды к одному типу. В случае же абстрактного реляционного сравнения, операнды сперва преобразуются в примитивы, затем приводятся к одному типу, и только после этого сравниваются.
Строгие сравнения (к примеру, ===) истинны только в том случае, если типы сравниваемых значений являются одинаковыми (к примеру: string-string, number-number). Однако, чаще используются сравнения с преобразованием типов (к примеру, ==). Такой тип сравнения, перед тем как непосредственно выполнить сравнение, приводит операнды к одному типу. В случае же абстрактного реляционного сравнения, операнды сперва преобразуются в примитивы, затем приводятся к одному типу, и только после этого сравниваются.
Строки сравниваются на основе стандартного лексикографического упорядочения, используя значения Unicode.
Особенности сравнений:
- Две строки строго равны только в том случае, если они имеют одинаковую длину, и те же символы в одинаковой последовательности и соответствующих позициях.
- Два числа строго равны в том случае, если они численно равны. NaN не равно ничему, в том числе и NaN. Нули с положительным и отрицательным знаком равны.
- Два логических значения (boolean) равны только в том случае, если они оба
истинны (true)илиложны (false).
- Два различных объекта никогда не равны как в строгих, так и в абстрактных сравнениях.
- Сравнение объекта истинно лишь в том случае, если оба операнда ссылаются на один и тот же объект в памяти.
- Виды
nullиundefinedравны себе как в строгом сравнении, так и в абстрактном.
При использовании сравнения с преобразованием типов, следует быть крайне осторожным, так как это может привести к непредвиденным проблемам, связанным с особенностями конвертации различных типов (см. параграф «Использование операторов равенства»).
Равно (==)
Оператор равно сначала приводит операнды к одному типу, и затем применяет строгое сравнение. Если оба операнда являются объектами, то JavaScript сравнивает внутренние ссылки, которые равны в том случае, если они ссылаются на один и тот же объект в памяти.
Синтаксис
x == y
Примеры
1 == 1
"1" == 1
1 == '1'
3 == 5
0 == false
"foo" == "bar"
Не равно (!=)
Оператор не равно возвращает true в том случае, если операнды не равны.![]() Он аналогичен оператору равенства, перед сравнением приводит операнды к одному типу. В случае если оба операнда являются объектами, JavaScript сравнивает внутренние ссылки, которые не равны в том случае, если относятся к разным объектам в памяти.
Он аналогичен оператору равенства, перед сравнением приводит операнды к одному типу. В случае если оба операнда являются объектами, JavaScript сравнивает внутренние ссылки, которые не равны в том случае, если относятся к разным объектам в памяти.
Синтаксис
x != y
Примеры
1 != 2
1 != "1"
1 != '1'
1 != true
0 != false
"foo" != "bar"
Строго равно (===)
Оператор возвращает истину в том случае, если операнды строго равны (см. выше). В отличие от оператора равно, данный оператор не приводит операнды к одному типу.
Синтаксис
x === y
Примеры
3 === 3
3 === '3'
'foo' === 'foo'
Строго не равно (!==)
Оператор строго не равно возвращает истину в том случае, если операнды не равны, или их типы отличаются друг от друга.
Синтаксис
x !== y
Примеры
3 !== '3'
4 !== 3
Больше (>)
Оператор больше возвращает истину в том случае, если значение левого операнда больше, чем правого.
Синтаксис
x > y
Примеры
4 > 3
1 > 5
Больше или равно (>=)
Оператор больше или равно, возвращает истину в том случае, если значение операнда слева больше или равно значению операнда справа.
Синтаксис
x >= y
Примеры
4 >= 3
3 >= 3
Меньше(<)
Оператор меньше, возвращает истину в том случае, если значение операнда слева меньше, чем значение операнда справа.
Синтаксис
x < y
Примеры
3 < 4
5 < 2
Меньше или равно (<=)
Оператор меньше или равно, возвращает истину в том случае, если значение операнда слева меньше, или равно значению операнда справа.
Синтаксис
x <= y
Примеры
3 <= 4
3 <= 3
Стандартные операции равенства с преобразованием типов (== и !=) используют Абстрактный Алгоритм Эквивалентного Сравнения для сравнения двух операндов. Если у операндов различные типы, то JavaScript пытается привести их к одному типу, перед тем как сравнивать их. К примеру, в выражении
Если у операндов различные типы, то JavaScript пытается привести их к одному типу, перед тем как сравнивать их. К примеру, в выражении 5 == '5', строка справа конвертируется в число, и только потом сравнивается.
Операторы строгого равентсва (=== и !==) используют Строгий Алгоритм Эквивалентного Сравнения, и предназначены для сравнения операндов одного типа. Если операнды имеют разные типы, то результат операции сравнения всегда будет ложью. К примеру, выражение 5 !== '5' будет истинным.
Используйте операторы строгого равенства в тех случаях, когда необходимо проверять не только значения операндов, но так же и их типы. Во противном случае, используйте операторы стандартного равенства, которые позволяют сравнить два операнда вне зависимости от их типов.
Когда происходит преобразование типов (т.е в случаях использования нестрогого сравнения), JavaScript преобразует типы String, Number, Boolean и Object, следующим образом:
- При сравнении числа
(Number)и строки(String), JavaScript пытается преобразовать числовой литерал строки в число. Затем полученное число округляется до ближайшего возможного значения типа
Затем полученное число округляется до ближайшего возможного значения типа Number. - Если один из операндов является логическим
(Boolean), то он преобразуется в значение типа(Number). Если значение логического операнда равняется истине(true), то значение этого операнда преобразуется в 1. Иначе — в 0(ложь / false). - Если объект сравнивается с числом или строкой, JavaScript пытается получить значение по умолчанию для данного объекта. Полученное значение преобразуется в примитив, посредством методов
valueOf()иtoString(). Если преобразовать объект не удается, генерируется ошибка времени выполнения. - Обратите внимание на то, что объект преобразуется в примитив, если, и только если, второй операнд является примитивом. В ином случае, операнды сравниваются как объекты, соответственно, операция сравнения вернет истину в том случае, если внутренние ссылки обоих объектов ссылаются на один и тот же объект в памяти.

Внимание: Объекты String имеют тип Object, а не String. Такие объекты используются редко, так что следующий код может вас сильно удивить.
'foo' === 'foo'
var a = new String('foo');
var b = new String('foo');
a == b
a === b
a == 'foo' | Chrome | Firefox (Gecko) | Internet Explorer | Opera | Safari | |
|---|---|---|---|---|---|
| Базовая поддержка | (Да) | (Да) | (Да) | (Да) | (Да) |
| Android | Chrome for Android | Firefox Mobile (Gecko) | IE Mobile | Opera Mobile | Safari Mobile | |
|---|---|---|---|---|---|---|
| Базовая поддержка | (Да) | (Да) | (Да) | (Да) | (Да) | (Да) |
Перечень специальных символов — Документация Qucs Help 0.
 0.19
0.19В компоненте “Текст” и в тексте меток осей диаграмм можно использовать специальные символы. Это делается с помощью тэгов LaTeX. В следующей таблице приводится перечень символов, имеющихся в настоящее время.
Примечание: Правильное отображение этих символов зависит от шрифта, используемого Qucs!
Строчные греческие буквы
| Тэг LaTeX | Юникод | Описание |
\alpha | 0x03B1 | alpha |
\beta | 0x03B2 | beta |
\gamma | 0x03B3 | gamma |
\delta | 0x03B4 | delta |
\epsilon | 0x03B5 | epsilon |
\zeta | 0x03B6 | zeta |
\eta | 0x03B7 | eta |
\theta | 0x03B8 | theta |
\iota | 0x03B9 | iota |
\kappa | 0x03BA | kappa |
\lambda | 0x03BB | lambda |
\mu | 0x03BC | mu |
\textmu | 0x00B5 | mu |
\nu | 0x03BD | nu |
\xi | 0x03BE | xi |
\pi | 0x03C0 | pi |
\varpi | 0x03D6 | pi |
\rho | 0x03C1 | rho |
\varrho | 0x03F1 | rho |
\sigma | 0x03C3 | sigma |
\tau | 0x03C4 | tau |
\upsilon | 0x03C5 | upsilon |
\phi | 0x03C6 | phi |
\chi | 0x03C7 | chi |
\psi | 0x03C8 | psi |
\omega | 0x03C9 | omega |
Прописные греческие буквы
| Тэг LaTeX | Юникод | Описание |
\Gamma | 0x0393 | Gamma |
\Delta | 0x0394 | Delta |
\Theta | 0x0398 | Theta |
\Lambda | 0x039B | Lambda |
\Xi | 0x039E | Xi |
\Pi | 0x03A0 | Pi |
\Sigma | 0x03A3 | Sigma |
\Upsilon | 0x03A5 | Upsilon |
\Phi | 0x03A6 | Phi |
\Psi | 0x03A8 | Psi |
\Omega | 0x03A9 | Omega |
Математические символы
| Тэг LaTeX | Юникод | Описание |
\cdot | 0x00B7 | знак умножения — точка (центрированная точка) |
\times | 0x00D7 | знак умножения — крестик |
\pm | 0x00B1 | знак плюс минус |
\mp | 0x2213 | знак минус плюс |
\partial | 0x2202 | знак частного дифференцирования |
\nabla | 0x2207 | набла-оператор |
\infty | 0x221E | знак бесконечности |
\int | 0x222B | знак интеграла |
\approx | 0x2248 | символ приближения (волнистый знак равенства) |
\neq | 0x2260 | знак не равно |
\in | 0x220A | символ “содержится в” |
\leq | 0x2264 | знак меньше-равно |
\geq | 0x2265 | знак больше-равно |
\sim | 0x223C | (центрально-европейский) знак пропорциональности |
\propto | 0x221D | (американский) знак пропорциональности |
\diameter | 0x00F8 | знак диаметра (также знак среднего) |
\onehalf | 0x00BD | половина |
\onequarter | 0x00BC | четверть |
\twosuperior | 0x00B2 | квадрат (степень 2) |
\threesuperior | 0x00B3 | степень 3 |
\ohm | 0x03A9 | единица для сопротивления (прописная греческая омега) |
back to the top
Справочник SQL для выражений запросов, применяемых в ArcGIS—ArcGIS Pro
This topic describes the elements of common selection queries in ArcGIS. Выражения запросов в ArcGIS используют SQL.
Выражения запросов в ArcGIS используют SQL.
Внимание:
Синтаксис SQL не работает при вычислении полей с помощью окна Калькулятора поля .
Часто используемые запросы: поиск строк
Строковые значения в выражениях всегда заключаются в одинарные кавычки, например:
STATE_NAME = 'California'
Строки в выражениях чувствительны к регистру, кроме случаев работы в базах геоданных в Microsoft SQL Server. Чтобы выполнять не чувствительный к регистру поиск в других источниках данных, можно использовать функцию SQL для преобразования всех значений в один регистр. Для источников данных на основе файлов, таких как файловые базы геоданных или шейп-файлы, для задания регистра выборки можно использовать функции UPPER или LOWER. Например, при помощи следующего выражения выбирается штат, имя которого написано как ‘Rhode Island’ или ‘RHODE ISLAND’:
UPPER(STATE_NAME) = 'RHODE ISLAND'
Если строка содержит одинарную кавычку, вам в первую очередь требуется использовать другую одинарную кавычку как символ управляющей последовательности, например:
NAME = 'Alfie''s Trough'
При помощи оператора LIKE (вместо оператора = ) строится поиск частей строк. Например, данное выражение выбирает Mississippi и Missouri среди названий штатов США:
Например, данное выражение выбирает Mississippi и Missouri среди названий штатов США:
STATE_NAME LIKE 'Miss%'
Символ процента (%) означает, что на этом месте может быть что угодно – один символ или сотня, или ни одного. Если вы хотите использовать групповой символ, обозначающий один любой символ, используйте символ подчёркивания (_). Следующий пример показывает выражение для выбора имен Catherine Smith и Katherine Smith:
OWNER_NAME LIKE '_atherine Smith'
Можно также использовать операторы больше (>), меньше (<), больше или равно (>=), меньше или равно (<=), не равно (<>) и BETWEEN, чтобы выбирать строковые значения на основании их сортировки. Например, этот запрос выбирает все города в покрытии, названия которых начинаются с букв от М до Z:
CITY_NAME >= 'M'
Строковые функции могут использоваться для форматирования строк. Например функция LEFT возвращает определенное количество символов начиная с левого края строки. Данный запрос возвращает все штаты, начинающиеся на букву A:
Данный запрос возвращает все штаты, начинающиеся на букву A:
LEFT(STATE_NAME,1) = 'A'
Список поддерживаемых функций вы найдете в документации по своей СУБД.
Часто используемые выражения: поиск значений NULL
Вы можете использовать ключевое слово NULL, чтобы отбирать объекты и записи, содержащие пустые поля. Перед ключевым словом NULL всегда стоит IS или IS NOT. Например, чтобы найти города, для которых не была введена численность населения по данным переписи 1996 года, можно использовать следующее выражение:
POPULATION IS NULL
Или, чтобы найти все города, для которых указана численность населения, используйте:
POPULATION96 IS NOT NULL
Часто используемые выражения: поиск чисел
Точка (.) всегда используется в качестве десятичного разделителя, независимо от региональных настроек. В выражениях в качестве разделителя десятичных знаков нельзя использовать запятую.
Вы можете запрашивать цифровые значения, используя операторы равно (=), не равно (<>), больше (>), меньше (<), больше или равно (>=) и меньше или равно (<=), а также BETWEEN (между), например:
POPULATION >= 5000
Числовые функции можно использовать для форматирования чисел. Например функция ROUND округляет до заданного количества десятичных знаков данные в файловой базе геоданных:
Например функция ROUND округляет до заданного количества десятичных знаков данные в файловой базе геоданных:
ROUND(SQKM,0) = 500
Список поддерживаемых числовых функций см. в документации по СУБД.
Даты и время
Общие правила и часто используемые выражения
В таких источниках данных, как база геоданных, даты хранятся в полях даты–времени. Однако в шейп-файлах это не тек. Поэтому большинство из примеров синтаксиса запроса, представленных ниже, содержит ссылки на время. В некоторых случаях часть запроса, касающаяся времени, может быть без всякого вреда пропущена, когда известно, что поле содержит только даты; в других случаях её необходимо указывать, или запрос вернет синтаксическую ошибку.
Поиск полей с датой требует внимания к синтаксису, необходимому для источника данных. Если вы создаете запрос в Конструкторе запросов в режиме Условие, правильный синтаксис будет сгенерирован автоматически. Ниже приведен пример запроса, который возвращает все записи после 1 января 2011, включительно, из файловой базы геоданных:
INCIDENT_DATE >= date '2011-01-01 00:00:00'
Даты хранятся в исходной базе данных относительно 30 декабря 1899 года, 00:00:00. Это действительно для всех источников данных, перечисленных здесь.
Это действительно для всех источников данных, перечисленных здесь.
Цель этого подраздела – помочь вам в построении запросов по датам, но не по значениям времени. Когда со значением даты хранится не нулевое значение (например January 12, 1999, 04:00:00), то запрос по дате не возвратит данную запись, поскольку если вы задаете в запросе только дату для поля в формате дата – время, недостающие поля времени заполняются нулями, и выбраны будут только записи, время которых соответствует 12:00:00 полуночи.
Таблица атрибутов отображает дату и время в удобном для пользователя формате, согласно вашим региональным установкам, а не в формате исходной базы данных. Это подходит для большинства случаев, но имеются и некоторые недостатки:
- Строка, отображаемая в SQL-запросе, может иметь только небольшое сходство со значением, показанным в таблице, особенно когда в нее входит время. Например время, введенное как 00:00:15, отображается в атрибутивной таблице как 12:00:15 AM с региональными настройками США, а сопоставимый синтаксис запроса Datefield = ‘1899-12-30 00:00:15’.

- Атрибутивная таблица не имеет сведений об исходных данных, пока вы не сохраните изменения. Она сначала попытается отформатировать значения в соответствии с ее собственным форматом, затем, после сохранения изменений, она попытается подогнать получившиеся результаты в соответствии с базой данных. По этой причине, вы можете вводить время в шейп-файл, но обнаружите, что оно удаляется при сохранении ваших изменений. Поле будет содержать значение ‘1899-12-30’, которое будет отображаться как 12:00:00 AM или эквивалентно, в зависимости от ваших региональных настроек.
Синтаксис даты-времени для многопользовательских баз геоданных
Oracle
Datefield = date 'yyyy-mm-dd'
Имейте в виду, что здесь записи, где время не равно нулю, не будут возвращены.
Альтернативный формат при запросах к датам в Oracle следующий:
Datefield = TO_DATE('yyyy-mm-dd hh:mm:ss','YYYY-MM-DD Hh34:MI:SS')Второй параметр ‘YYYY-MM-DD Hh34:MI:SS’ описывает используемый при запросах формат. Актуальный запрос выглядит так:
Актуальный запрос выглядит так:
Datefield = TO_DATE('2003-01-08 14:35:00','YYYY-MM-DD Hh34:MI:SS')Вы можете использовать более короткую версию:
TO_DATE('2003-11-18','YYYY-MM-DD')И снова записи, где время не равно нулю, не будут возвращены.
SQL Server
Datefield = 'yyyy-mm-dd hh:mm:ss'
Часть запроса hh:mm:ss может быть опущена, когда в записях не установлено время.
Ниже приведен альтернативный формат:
Datefield = 'mm/dd/yyyy'
IBM Db2
Datefield = TO_DATE('yyyy-mm-dd hh:mm:ss','YYYY-MM-DD Hh34:MI:SS')Часть запроса hh:mm:ss не может быть опущена, даже если время равно 00:00:00.
PostgreSQL
Datefield = TIMESTAMP 'YYYY-MM-DD Hh34:MI:SS' Datefield = TIMESTAMP 'YYYY-MM-DD'
Вы должны указать полностью временную метку при использовании запросов типа «равно», в или не будет возвращено никаких записей. Вы можете успешно делать запросы со следующими выражениями, если запрашиваемая таблица содержит записи дат с точными временными метками (2007-05-29 00:00:00 или 2007-05-29 12:14:25):
Вы можете успешно делать запросы со следующими выражениями, если запрашиваемая таблица содержит записи дат с точными временными метками (2007-05-29 00:00:00 или 2007-05-29 12:14:25):
select * from table where date = '2007-05-29 00:00:00';
или
select * from table where date = '2007-05-29 12:14:25';
При использовании других операторов, таких как больше, меньше, больше или равно, или меньше или равно, вам не нужно указывать время, но это можно сделать для повышения точности. Оба эти выражения работают:
select * from table where date < '2007-05-29';
select * from table where date < '2007-05-29 12:14:25';
Файловые базы геоданных, шейп-файлы, покрытия и прочие файловые источники данных
Datefield = date 'yyyy-mm-dd'
Файловые базы геоданных поддерживают использование времени в поле даты, поэтому его можно добавить в выражение:
Datefield = date 'yyyy-mm-dd hh:mm:ss'
Шейп-файлы и покрытия не поддерживают использование времени в поле даты.
SQL, используемый в файловой базе геоданных, базируется на стандарте SQL-92.
Известные ограничения
Построение запросов к датам, находящимся в левой части (первой таблице) соединения, работает только для файловых источников данных, таких как файловые базы геоданных, шейп-файлы и таблицы DBF. Но возможен обходной путь при работе с другими, не файловыми, источниками, такими как многопользовательские данные, как описано ниже.
Запрос к датам левой части соединения будет выполнен успешно, если использовать ограниченную версию SQL, разработанную для файловых источников данных. Если вы не используете такой источник данных, можете перевести выражение для использования этого формата. Нужно обеспечить, чтобы выражение запроса включало поля из более чем одной присоединенной таблицы. Например, если соединены класс пространственных объектов и таблица (FC1 и Table1), и они поступают из многопользовательской базы геоданных, следующее выражение не будет выполнено или не вернет данные:
FC1.date = date #01/12/2001# FC1.date = date '01/12/2001'
Чтобы запрос был выполнен успешно, можно создать вот такой запрос:
FC1.date = date '01/12/2001' and Table1.OBJECTID > 0
Так как запрос включает поля из обеих таблиц, будет использована ограниченная версия SQL. В этом выражении Table1.OBJECTID всегда > 0 для записей, которые сопоставлены в процессе создания соединения, поэтому это выражение всегда верно для всех строк, содержащих сопоставления соединения.
Чтобы быть уверенным, что каждая запись с FC1.date = date ’01/12/2001′ выбрана, используйте следующий запрос:
FC1.date = date '01/12/2001' and (Table1.OBJECTID IS NOT NULL OR Table1.OBJECTID IS NULL)
Такой запрос будет выбирать все записи с FC1.date = date ’01/12/2001′, независимо от того, есть ли сопоставление при соединении для каждой отдельной записи.
Комбинированные выражения
Составные запросы могут комбинироваться путем соединения выражений операторами AND (И) и OR (ИЛИ). Вот пример запроса для выборки всех домов с общей площадью более 1500 квадратных футов и гаражом более чем на три машины:
Вот пример запроса для выборки всех домов с общей площадью более 1500 квадратных футов и гаражом более чем на три машины:
AREA > 1500 AND GARAGE > 3
Когда вы используете оператор OR (ИЛИ), по крайней мере одно из двух разделенных оператором выражений, должно быть верно для выбираемой записи, например:
RAINFALL < 20 OR SLOPE > 35
Используйте оператор NOT (НЕ) в начале выражения, чтобы найти объекты или записи, не соответствующие условию выражения, например:
NOT STATE_NAME = 'Colorado'
Оператор NOT можно комбинировать с AND и OR. Вот пример запроса, который выбирает все штаты Новой Англии за исключением штата Maine:
SUB_REGION = 'New England' AND NOT STATE_NAME = 'Maine'
Вычисления
Вычисления можно включить в запросы с помощью математических операторов +, –, * и /. Можно использовать вычисление между полем и числом, например:
AREA >= PERIMETER * 100
Вычисления также могут производиться между полями.![]() Например чтобы найти районы с плотностью населения меньшим или равным 25 человек на 1 квадратную милю, можно использовать вот такой запрос:
Например чтобы найти районы с плотностью населения меньшим или равным 25 человек на 1 квадратную милю, можно использовать вот такой запрос:
POP1990 / AREA <= 25
Приоритет выражения в скобках
Выражения выполняются в последовательности, определяемой стандартными правилами. Например, заключённая в круглые скобки часть выражения выполняется раньше, чем часть выражения за скобками.
HOUSEHOLDS > MALES * (POP90_SQMI + AREA)
Вы можете добавить скобки в режиме Редактирование SQL вручную, или использовать команды Группировать и Разгруппировать в режиме Условие, чтобы добавить или удалить их.
Подзапросы
Подзапрос – это запрос, вложенный в другой запрос и поддерживаемый только в базах геоданных. Подзапросы могут использоваться в SQL-выражении для применения предикативных или агрегирующих функций, или для сравнения данных со значениями, хранящимися в другой таблице и т.п. Это может быть сделано с помощью ключевых слов IN или ANY.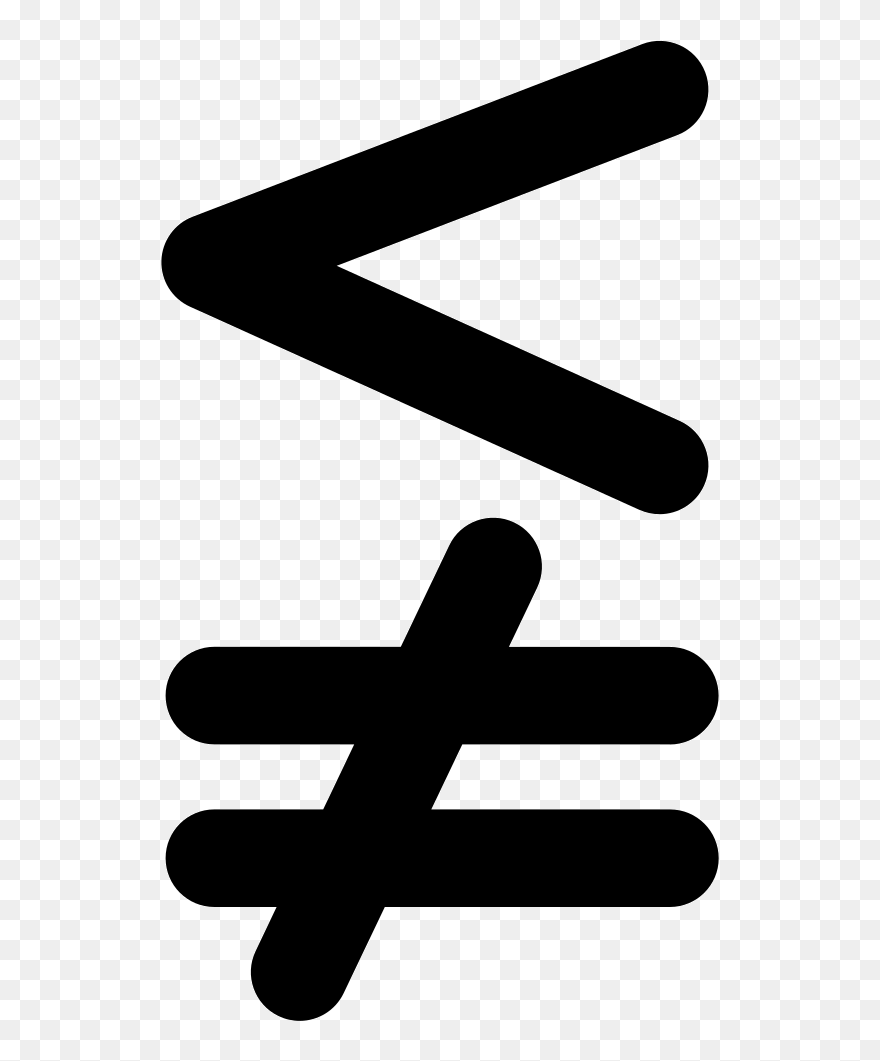 Например этот запрос выбирает только те страны, которых нет в таблице indep_countries:
Например этот запрос выбирает только те страны, которых нет в таблице indep_countries:
COUNTRY_NAME NOT IN (SELECT COUNTRY_NAME FROM indep_countries)
Покрытия, шейп-файлы и прочие файловые источники данных, не относящиеся к базам геоданных, не поддерживают подзапросы. Подзапросы, выполняемые на версионных многопользовательских классах объектов и таблицах, не возвращают объекты, которые хранятся в дельта-таблицах. Файловые базы геоданных имеют ограниченную поддержку подзапросов, описанных в данном разделе, в то время, как многопользовательские базы геоданных поддерживают их полностью. Информацию обо всех возможностях подзапросов к многопользовательским базам геоданных смотрите в документации по своей СУБД.
Этот запрос возвращает объекты, где GDP2006 больше, чем GDP2005 любых объектов, содержащихся в countries (странах):
GDP2006 > (SELECT MAX(GDP2005) FROM countries)
Поддержка подзапросов в файловых базах геоданных ограничена следующим:
Операторы
Ниже приведен полный список операторов, поддерживаемых файловыми базами геоданных, шейп-файлами, покрытиями и прочими файловыми источниками данных. Они также поддерживаются в многопользовательских базах геоданных, хотя для этих источников данных может требоваться иной синтаксис. Кроме нижеперечисленных операторов, многопользовательские базы геоданных поддерживают дополнительные возможности. Более подробную информацию см. в документации по своей СУБД.
Они также поддерживаются в многопользовательских базах геоданных, хотя для этих источников данных может требоваться иной синтаксис. Кроме нижеперечисленных операторов, многопользовательские базы геоданных поддерживают дополнительные возможности. Более подробную информацию см. в документации по своей СУБД.
Арифметические операторы
Для сложения, вычитания, умножения и деления числовых значений можно использовать арифметические операторы.
| Оператор | Описание |
|---|---|
* | Арифметический оператор умножения |
/ | Арифметический оператор деления |
+ | Арифметический оператор сложения |
– | Арифметический оператор вычитания |
Операторы сравнения
Операторы сравнения используются для сравнения одного выражения с другим.
| Оператор | Описание |
|---|---|
< | Меньше . Может использоваться со строками (сравнение основывается на алфавитном порядке) и для числовых вычислений, а также дат. |
<= | Меньше или равно. Может использоваться со строками (сравнение основывается на алфавитном порядке) и для числовых вычислений, а также дат. |
<> | Не равно . Может использоваться со строками (сравнение основывается на алфавитном порядке) и для числовых вычислений, а также дат. |
> | Больше . |
>= | Больше или равно. Может использоваться со строками (сравнение основывается на алфавитном порядке) и для числовых вычислений, а также дат. |
[NOT] BETWEEN x AND y | Выбирает запись, если она имеет значение, которое больше или равно x и меньше или равно y. Если перед ней стоит значение NOT, она выбирает запись, если та имеет значение вне указанного диапазона. Например это выражение выбирает все записи со значениями, которые больше или равны 1 и меньше или равны 10: OBJECTID BETWEEN 1 AND 10 Вот эквивалент этого выражения: OBJECTID >= 1 AND OBJECTID <= 10 Однако, выражение с оператором BETWEEN обрабатывается быстрее, если у вас поле проиндексировано. |
[NOT] EXISTS | Возвращает TRUE (истинно), если подзапрос возвращает хотя бы одну запись; в противном случае возвращает FALSE (ложно). Например, данное выражение вернет TRUE, если поле OJBECTID содержит значение 50: EXISTS (SELECT * FROM parcels WHERE OBJECTID = 50) EXISTS поддерживается только в файловых и многопользовательских базах геоданных. |
[NOT] IN | Выбирает запись, если она содержит одну из нескольких строк или значений в поле. Если впереди стоит NOT, выбирает запись, где нет таких строк или значений. Например, это выражение будет искать четыре разных названия штатов: STATE_NAME IN ('Alabama', 'Alaska', 'California', 'Florida') |
IS [NOT] NULL | Выбирает запись, если там в определенном поле есть нулевое значение. |
x [NOT] LIKE y [ESCAPE ‘escape-character’] | Используйте оператор LIKE (вместо оператора = ) с групповыми символами, если хотите построить запрос по части строки. Символ процента (%) означает, что на этом месте может быть что угодно – один символ или сотня, или ни одного. Если вы хотите использовать групповой символ, обозначающий один любой символ, используйте символ подчёркивания (_). Если вам нужен доступ к несимвольным данным, используйте функцию CAST. Например, этот запрос возвращает числа, начинающиеся на 8, из целочисленного поля SCORE_INT: CAST (SCORE_INT AS VARCHAR(10)) LIKE '8%' Для включения символа (%) или (_) в вашу строку поиска, используйте ключевое слово ESCAPE для указания другого символа вместо escape, который в свою очередь обозначает настоящий знак процента или подчёркивания. AMOUNT LIKE '%10$%%' ESCAPE '$' |
Логические операторы
| Оператор | Описание |
|---|---|
AND | Соединяет два условия и выбирает запись, в которой оба условия являются истинными. Например, выполнение следующего запроса выберет все дома с площадью более 1 500 квадратных футов и гаражом на две и более машины: AREA > 1500 AND GARAGE > 2 |
OR | Соединяет два условия и выбирает запись, где истинно хотя бы одно условие. AREA > 1500 OR GARAGE > 2 |
NOT | Выбирает записи, не соответствующие указанному выражению. Например это выражение выберет все штаты, кроме Калифорнии (California): NOT STATE_NAME = 'California' |
Операторы строковой операции
| Оператор | Описание |
|---|---|
|| | Возвращает символьную строку, являющуюся результатом конкатенации двух или более строковых выражений. FIRST_NAME || MIDDLE_NAME || LAST_NAME |
Функции
Ниже приведен полный список функций, поддерживаемых файловыми базами геоданных, шейп-файлами, покрытиями и прочими файловыми источниками данных. Функции также поддерживаются в многопользовательских базах геоданных, хотя в этих источниках данных может использоваться иной синтаксис или имена функций. Кроме нижеперечисленных функций, многопользовательские базы геоданных поддерживают дополнительные возможности. Более подробную информацию см. в документации по своей СУБД.
Функции дат
| Функция | Описание |
|---|---|
CURRENT_DATE | Возвращает текущую дату. |
EXTRACT(extract_field FROM extract_source) | Возвращает фрагмент extract_field из extract_source. |
CURRENT TIME | Возвращает текущую дату. |
Строковые функции
Аргументы, обозначаемые string_exp, могут быть названием столбца, строковой константой или результатом другой скалярной функции, где исходные данные могут быть представлены в виде символов.
Аргументы, обозначаемые character_exp, являются строками символов переменной длины.
Аргументы, указанные как start или length могут быть числовыми постоянными или результатами других скалярных функций, где исходные данные представлены числовым типом.
Строковые функции, перечисленные здесь, базируются на 1; то есть, первым символом в строке является символ 1.
| Функция | Описание |
|---|---|
CHAR_LENGTH(string_exp) | Возвращает длину строкового выражения в символах. |
LOWER(string_exp) | Возвращает строку, идентичную string_exp, в которой все символы верхнего регистра изменены на символы нижнего регистра. |
POSITION(character_exp IN character_exp) | Возвращает место первого символьного выражения во втором символьном выражении. Результат – число с точностью, определяемой реализацией и коэффициентом кратности 0. |
SUBSTRING(string_exp FROM start FOR length) | Возвращает символьную строку, извлекаемую из string_exp, начинающуюся с символа, положение которого определяется символами start и length . |
TRIM(BOTH | LEADING | TRAILING trim_character FROM string_exp) | Возвращает string_exp, укороченную на количество символов, указанное в аргументе trim_character, с начала, с конца или с обоих концов строки. |
UPPER(string_exp) | Возвращает строку, идентичную string_exp, в которой все символы нижнего регистра изменены на символы верхнего регистра. |
Числовые функции
Все числовые функции возвращают числовые значения.
Аргументы, обозначенные numeric_exp, float_exp или integer_exp могут быть именем столбца, результатом другой скалярной функции или числовой константой, где исходные данные могут быть представлены числовым типом.
| Функция | Описание |
|---|---|
ABS(numeric_exp) | Возвращает абсолютное значение numeric_exp. |
ACOS(float_exp) | Возвращает угол в радианах, равный арккосинусу float_exp. |
ASIN(float_exp) | Возвращает угол в радианах, равный арксинусу float_exp. |
ATAN(float_exp) | Возвращает угол в радианах, равный арктангенсу float_exp. |
CEILING(numeric_exp) | Возвращает наименьшее целочисленное значение, большее или равное numeric_exp. |
COS(float_exp) | Возвращает косинус float_exp, где float_exp — угол, выраженный в радианах. |
FLOOR(numeric_exp) | Возвращает наибольшее целое значение, меньшее или равное numeric_exp. |
LOG(float_exp) | Возвращает натуральный логарифм float_exp. |
LOG10(float_exp) | Возвращает логарифм по основанию 10 float_exp. |
MOD(integer_exp1, integer_exp2) | Возвращает результат деления integer_exp1 на integer_exp2. |
POWER(numeric_exp, integer_exp) | Возвращает значение numeric_exp в степени integer_exp. |
ROUND(numeric_exp, integer_exp) | Возвращает numeric_exp, округленное до integer_exp знаков справа от десятичной точки. Если integer_exp отрицательное, numeric_exp округляется до |integer_exp| знаков слева от десятичной запятой. |
SIGN(numeric_exp) | Возвращает указатель знака numeric_exp. Если numeric_exp меньше нуля, возвращается -1. Если numeric_exp равно нулю, возвращается 0. Если numeric_exp больше нуля, возвращается 1. |
SIN(float_exp) | Возвращает синус float_exp, где float_exp — угол, выраженный в радианах. |
TAN(float_exp) | Возвращает тангенс float_exp, где float_exp — угол, выраженный в радианах. |
TRUNCATE(numeric_exp, integer_exp) | Возвращает numeric_exp, округленное до integer_exp знаков справа от десятичной точки. Если integer_exp отрицательное, numeric_exp округляется до |integer_exp| знаков слева от десятичной запятой. |
Функция CAST
Функция CAST конвертирует значение в определенный тип данных. Синтаксис выглядит так:
CAST(exp AS data_type [(length)])
Пример:
CAST (SCORE_INT AS VARCHAR(10))
Аргумент exp может быть названием столбца, результатом другой скалярной функции или буквенным. Data_type может быть любым из следующих ключевых слов, и задается строчными или заглавными буквами: CHAR, VARCHAR, INTEGER, SMALLINT, REAL, DOUBLE, DATE, TIME, DATETIME, NUMERIC или DECIMAL.
Data_type может быть любым из следующих ключевых слов, и задается строчными или заглавными буквами: CHAR, VARCHAR, INTEGER, SMALLINT, REAL, DOUBLE, DATE, TIME, DATETIME, NUMERIC или DECIMAL.
Более подробно о функции CAST см. CAST and CONVERT.
Связанные разделы
Отзыв по этому разделу?
Ruby/Базовые типы данных — Викиучебник
Все абстрактные типы данных
Базовые типы данных[править]
Данные любого типа в Ruby суть объекты тех или иных классов. Самые используемые встроенные типы данных:
Естественно, что это только базовые типы, но их вполне хватает для широкого спектра задач.
Числа[править]
Числа в Ruby выглядят так:
5 # целое число -12 # отрицательное целое число 4.5 # число с плавающей точкой 076 # восьмеричное число 0b010 # двоичное число 0x89 # шестнадцатеричное число
Не будем пока углубляться и мельком взглянем на другие типы данных.
Логический тип[править]
Логический (булевый) тип — это вариация на тему «да» или «нет».
xorМетоды сравнения[править]
| Название метода | Символ |
|---|---|
| Равно | == |
| Не равно | != |
| Меньше | < |
| Больше | > |
| Меньше или равно | <= |
| Больше или равно | >= |
Часто молодые программисты, когда надо написать «меньше или равно», пишут знак =< вместо <=. Запомнить правильное написание можно вслух проговорив «меньше или равно» и в этом же порядке писать < и =.
- Традиционно имена логических методов заканчиваются на
?(знак вопроса). - В качестве
falseможет выступатьnil, а в качествеtrue— любой объект. nil— это символ пустоты.
Массивы[править]
Разработчики Ruby решили не реализовывать особых классов для динамических массивов, списков, стеков и тому подобного. Они все это реализовали в массивах — структурах данных типа (или класса — в Ruby всё равно) Array. Сделано это путём добавления специальных методов; например, методы .push и .pop для стека. Особенности массивов в Ruby:
- Нет ограничений (это общий принцип языка). Массивы могут быть сколь угодно длинными.
- Динамичность: размер массива легко меняется.
- Гетерогенность: один массив может хранить данные разных типов.
- Библиотека итераторов на каждый случай жизни. Эта возможность позволяет не использовать циклы для обработки данных в массивах, а, следовательно, избегать множества ошибок, связанных с неосторожным обращением с циклами. Итераторы реализуются на высочайшем уровне.
- Много других методов. Все элементарные задачи для массивов решаются вызовом нужного метода.

[1, 0, 740, 14, 25] # целочисленный массив
["a", "й", "6", 'Br', "Это массив строк, о них вы скоро узнаете"]
[[1, 2], [3, 4]] # двумерный целочисленный массив
# Матрица — это объект класса Matrix
# Двумерный массив — это не матрица целых чисел
["1-й элемент смешанного массива", "7.343", [4, "вепрь"],
[3, 67, 4326, 12, 3781357, 84221, "строка делает этот подмассив смешанным, но это не беда"]]
array = ["Этот массив пойдёт в переменную array", "Як-цуп-цоп, парви каридулла"]
Массив лучше всего вообразить как гусеницу или поезд с лапками-запятыми вместо колёс. Ползёт он всегда влево, на левом же конце его локомотив — первый элемент. Первый потому, что элементы упорядочены. Если знаете порядковый номер элемента, то легко получить его значение:
array[1] #=> "Як-цуп-цоп, парви каридулла"
В мире поездов-гусениц счёт вагонов начинается с локомотива, а не со следующего за ним вагона. Таким образом локомотив — это как бы нулевой вагон.
array[0] #=> "Этот массив пойдёт в переменную array"
Массивы кажутся странными с кавычками, но частенько бывают полезны при написании компьютерных программ. Возможно, вы даже поймёте, почему он ползёт всегда влево.
Строки[править]
Стро́ки — это ряды букв и других символов. В Ruby стро́ки используют наработки языка Perl. Вот небольшой список их возможностей:
- Нет ограничений. Длина строки́ может достигать поистине фантастических размеров.
- Динамичность. Стро́ки можно расширять или уменьшать (для этого есть методы
+и[]). - Любой объект преобразуется в строку (методы
.inspectи.to_sесть у любого объекта). - Строка обладает обширной библиотекой методов, которые работают с правилами (это методы
.gsub,.match,.scan,.split).
Правила — это новое название регулярных выражений. |
- Можно вставлять произвольныe переменные заключив их между
#{и}. Действует для строк начинающихся и заканчивающихся". После выполнения код заместится результатом.
Стро́ки начинаются и заканчиваются " (программистскими кавычками) или ' (машинописным апострофом). Пример:
"мама мыла раму" # строка в кавычках 'рама сопротивлялась' # строка в апострофах
Стро́ки подобны массивам символов, поэтому их часто преобразуют к массивам, чтобы использовать богатый набор методов, а потом результат делают строкой.
Ассоциативные массивы[править]
Ассоциативные массивы подобны массивам упорядоченных пар. Работают они подобно словарям: фигурная скобка символизирует боковой вид на открытую книгу, а стрелка => покажет читателю связь каждой сущности с какой-то другой. Вторая фигурная скобка говорит, что пора закрывать книгу. В Ruby такие массивы именуются Hash
Вторая фигурная скобка говорит, что пора закрывать книгу. В Ruby такие массивы именуются Hash
hash = {"мама"=>"мыла раму", 807=>"Это число улыбается!"}
Но можно и без фигурных скобок, одной стрелкой:
"Превед"=>"Медвед"
Например:
puts hash["мама"] #=> мыла раму puts hash["807"] #=> nil puts hash[807] #=> Это число улыбается! puts hash[1] #=> nil puts hash["Превед"] #=> Медвед
Ассоциативные массивы оставляют возможность хранения данных разного типа только в ассоциативном виде.
Диапазоны значений[править]
Чтобы было удобней получать подмассив или подстроку, был введён простенький тип данных — диапазон (класс Range). Диапазон формируется тремя элементами: начало, конец и тип протяжённости (символ .. или ...). Начало и конец должны быть одного типа данных (одного класса) и быть перечисляемыми, что значит, иметь метод .succ. Пример диапазонов:
"a".."z" "a"..."z" # то же, что и "a".."y" 1..100 1...100 # то же, что и 1..99
Диапазон-мотоцикл (..) проезжает от первого указанного объекта к его .succ (succedent — «последующему»), и до последнего включительно. Три точки — то же, но мотоцикл остановился прямо перед последним элементом. Ещё раз:
1..99 ≣ 1...100
Объекты, имеющие .succ называют последовательными: этим методом можно по текущему элементу достоверно определить следующий.
Классы и объекты[править]
Самодельные и неабстрактные составные типы данных называются классами. Если для вас это новость, то почитайте викиучебник об объектно-ориентированном программировании или статью в Википедии. Вообще, в Ruby всё в конечном счёте принадлежит классу Object.
str = "Я - строка" str.class #=> String str.class.superclass #=> Object
Классы можно определять и создавать по ним объекты. Стоит отметить интересную особенность языка — описание класса здесь это не просто некая описательная конструкция, не имеющая типа (как, например, в C++), а это объект (!) класса Class, дополненный пользовательскими методами и полями. Внутри класса может быть много всего интересного, и у него может быть фамильное дерево, то есть классы Ruby поддерживают наследование. Однако заметим, что множественное наследование в Ruby не разрешается. И ещё много всего интересного можно сделать с классами и объектами. Но об этом позже.
Внутри класса может быть много всего интересного, и у него может быть фамильное дерево, то есть классы Ruby поддерживают наследование. Однако заметим, что множественное наследование в Ruby не разрешается. И ещё много всего интересного можно сделать с классами и объектами. Но об этом позже.
Nemeth Tutorial — Урок 8.2
Знак плюс или минус
Брайлевский символ для знака плюс или минус, точки три четыре шесть точек три шесть, состоит из знака плюс, за которым следует знак минус. Эквивалент этого символа при печати — знак плюса над знаком минус в вертикальном расположении. Хотя они редко используются, знак минуса или плюса, точки три шесть точек три четыре шесть, имеет то же значение, что и знак плюс или минус. Студенты должны помнить, что использование знака плюс или минус указывает на то, что на самом деле есть два ответа.
Иногда два символа плюса и минуса соединяются горизонтально при печати. На шрифте Брайля между двумя знаками работы находится многоцелевой индикатор — точка пять. Это указывает на то, что два символа печатаются горизонтально, а не вертикально. Ниже приведены возможные комбинации этих знаков:
Это указывает на то, что два символа печатаются горизонтально, а не вертикально. Ниже приведены возможные комбинации этих знаков:
плюс, за которым следует минус, точки три четыре шесть точек пять точек три шесть
минус, за которым следует плюс, точки три шесть точек пять точек три четыре шесть
плюс, за которым следует плюс, точки три четыре шесть точек пять точек три четыре шесть
минус, за которым следует минус, точки три шесть точек пять точек три шесть
Варианты знака равенства
Знаки сравнения можно использовать вместе, и иногда они отображаются в печати как объединенные двумя различными способами.Один из способов — наложить один символ поверх другого с чрезмерным выделением. Второй способ — соединить их по вертикали, поместив один символ над другим. В шрифте Брайля комбинация отображается горизонтально. Когда знаки сравнения сочетаются с другими знаками сравнения, не ставьте между ними пробел.
Знаки сравнения также можно отрицать, представляя понятие «не». В печати отрицание представлено вертикальной линией или левой или правой косой чертой по диагонали напротив знака сравнения.В шрифте Брайля знак сравнения аннулируется, если перед символом ставятся точки три четыре. Знак отрицания должен быть первым символом, следующим за пробелом, который предшествует знаку сравнения, и не должен находиться на расстоянии от своего сопутствующего знака. Поскольку перед знаком сравнения и после него требуется пробел, косая черта не может быть ошибочно принята за знак операции.
В печати отрицание представлено вертикальной линией или левой или правой косой чертой по диагонали напротив знака сравнения.В шрифте Брайля знак сравнения аннулируется, если перед символом ставятся точки три четыре. Знак отрицания должен быть первым символом, следующим за пробелом, который предшествует знаку сравнения, и не должен находиться на расстоянии от своего сопутствующего знака. Поскольку перед знаком сравнения и после него требуется пробел, косая черта не может быть ошибочно принята за знак операции.
Знак отличия
Знак «не равно», точки три четыре точки четыре шесть точек одна три, используется аналогично знаку равенства.Его смысл, однако, просто в том, что суммы по обе стороны от него не идентичны. Знак не равно соответствует правилам для знаков сравнения.
Вопросительный знак над равно
В печати иногда ставится вопросительный знак над равным. Его смысл состоит в том, чтобы спросить, действительно ли суммы по обе стороны от равного идентичны. Знак вопроса над равным — точка пять точек четыре шесть точек одна три точки одна две шесть точек четыре пять шесть точек два три шесть точек один два четыре пять шесть.Таким образом, это многоцелевой индикатор, точка пять, за которым следует знак равенства, поднятый выше символ, индикатор пунктуации, вопросительный знак и, наконец, индикатор завершения.
Знак вопроса над равным — точка пять точек четыре шесть точек одна три точки одна две шесть точек четыре пять шесть точек два три шесть точек один два четыре пять шесть.Таким образом, это многоцелевой индикатор, точка пять, за которым следует знак равенства, поднятый выше символ, индикатор пунктуации, вопросительный знак и, наконец, индикатор завершения.
Пример 1
и PlusMinus; 31
⠬⠤⠒⠂
Пример 2
7 и PlusMinus; 3
⠼⠶⠬⠤⠒
Пример 3
6 & mp; 4
⠼⠖⠤⠬⠲
Пример 4
-5 + -2
⠤⠼⠢⠬⠐⠤⠆
Пример 5
7–3
⠼⠶⠤⠐⠤⠒
Пример 6
3 + 5 15
Пример 7
3 + 5 & equest; 15
⠼⠒⠬⠢⠀⠐⠨⠅⠣⠸⠦⠻⠀⠼⠂⠢
предыдущая — следующая (упражнения)
Примечание: доступность веб-сайтов APH
История символов равенства в математике
Представьте себе попытку написать математическое уравнение словами.Для задач вычислений более низкого уровня это было бы достаточно сложно, но для более длинных задач алгебры и исчисления написание уравнения словами могло занять несколько страниц. Использование математических символов требует меньше времени и места. Кроме того, математические символы имеют международный характер, позволяя людям обмениваться информацией с помощью символов, которые они не могут передать словами.
Использование математических символов требует меньше времени и места. Кроме того, математические символы имеют международный характер, позволяя людям обмениваться информацией с помощью символов, которые они не могут передать словами.
Знак равенства
До того, как знак равенства стал широко использоваться, равенство выражалось словами. По словам Ланкхэма, Нахтергэле и Шиллинга из Калифорнийского университета в Дэвисе, первое использование знака равенства (=) произошло в 1557 году.Роберт Рекорд, живший примерно в 1510–1558 годах, был первым, кто использовал этот символ в своей работе «Точильный камень Витте». Рекорд, валлийский врач и математик, использовал две параллельные линии для обозначения равенства, потому что считал, что это самые равные вещи из всех существующих.
Неравенства
Знаки «больше» (>) и «меньше» (<) были введены в 1631 году в «Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas». Книга была работой британского математика Томаса Харриота и была опубликована через 10 лет после его смерти в 1621 году.Символы на самом деле были придуманы редактором книги. Харриот изначально использовал треугольные символы, которые редактор изменил, чтобы они напоминали современные символы «меньше / больше». Интересно, что Харриот также использовал параллельные линии для обозначения равенства. Однако знак равенства Харриота был вертикальным (II), а не горизонтальным (=).
Книга была работой британского математика Томаса Харриота и была опубликована через 10 лет после его смерти в 1621 году.Символы на самом деле были придуманы редактором книги. Харриот изначально использовал треугольные символы, которые редактор изменил, чтобы они напоминали современные символы «меньше / больше». Интересно, что Харриот также использовал параллельные линии для обозначения равенства. Однако знак равенства Харриота был вертикальным (II), а не горизонтальным (=).
Меньше / больше или равно
Символы «меньше / больше или равно» (<и>) с одной линией знака равенства под ними были впервые использованы в 1734 году французским математиком Пьером Бугером.Джон Уоллис, британский логик и математик, использовал похожие символы в 1670 году. Уоллис использовал символы «больше / меньше» с одной горизонтальной линией над ними.
Равно по определению
В алгебре используется несколько символов для обозначения «равных по определению». Современные символы: (: =), (?) И (≡). Равные по определению впервые появились в книге «Logica Matematica» Чезаре Бурали-Форти, итальянского математика, жившего в 1861–1931 годах. Бурали-Форти фактически использовал символ (= Def).
Современные символы: (: =), (?) И (≡). Равные по определению впервые появились в книге «Logica Matematica» Чезаре Бурали-Форти, итальянского математика, жившего в 1861–1931 годах. Бурали-Форти фактически использовал символ (= Def).
Не равно
Современный знак «не равно» — это знак равенства с косой чертой. Этот символ приписывается Леонарду Эйлеру, швейцарскому математику, жившему с 1707 по 1783 год.
Опубликовано K12 Handhelds, Inc.
Портал, Аризона
www.k12handhelds.com
Авторские права © 2008, K12 Handhelds, Inc. Лицензия CC-by,
Эта работа находится под лицензией Creative Commons Attribution 3.0 United States License.
Разработано совместно со школьной системой Wayne Township.
Неравенство — это математическое утверждение, которое говорит о двух выражениях, которые не равны. Неравенства могут показать выражение, которое больше или меньше чем-то.
Эти символы используются в неравенствах:
Больше
(Вы можете запомнить это, потому что сначала идет больший открытый конец. )
)
Менее
(Вы можете запомнить это, потому что меньший закрытый конец идет первым.)
Больше или равно
(Линия под символом означает равно.)
Меньше или равно
Когда мы читаем неравенство, мы читаем его слева направо.
Вот несколько примеров.
10 7
Десять больше 7.
х 9
x меньше 9.
п. 5
p меньше или равно 5.
л 4
y больше или равно 4.
Попробуйте прочитать это самостоятельно:
х 9
10 2
т 3
к 2
9 6
м 2
Часто проще всего поместить переменную, например x, в левую часть уравнения.
Неравенство можно переписать в обратном направлении; просто убедитесь, что вы перевернули знак неравенства.
Например,
3 х
можно переписать как
x 3.
Самый простой способ запомнить это — убедиться, что маленький конец символа указывает на то же число. В этом случае маленький конец символа <указывает на x в обоих случаях.
В этом случае маленький конец символа <указывает на x в обоих случаях.
Чтобы перевести слова в неравенство, сначала решите, какой символ использовать.Являются ли описываемые вещи больше, меньше, больше или равны, меньше или равны чему-либо?
Затем выясните, какое выражение больше, и поместите его на больший (открытый) конец символа. Поместите другое выражение на другую сторону. Помните, что неизвестное может быть представлено с помощью x или другой буквенной переменной.
Например, давайте запишем выражение «x меньше трех» как неравенство. Слова «меньше» говорят нам использовать знак <.x меньше чем, поэтому он идет на закрытый конец символа. Неравенство:
x 3
Как насчет неравенства «Покупка 10 галлонов газа будет стоить более 30 долларов»?
«More» говорит нам использовать>. Цена за галлон неизвестна, поэтому мы будем использовать для этого x. Цена 10 галлонов (10x) будет больше 30 долларов, так что у нас:
10x 30
Как бы вы написали «Все три кошки вместе весят менее 10 фунтов» в качестве неравенства? Подсказка: мы не знаем веса ни одной из кошек (и они не обязательно весят одинаковое количество). ) Вот неравенство:
) Вот неравенство:
а + б + в 10
(Вы можете использовать любые три буквы для переменных, если они отличаются друг от друга.)
Давай сделаем еще один. Запишите это неравенством: «Цена автомобиля не более 3000 долларов».
Ответ:
п. 3,000
Нам нужно использовать символ «меньше или равно», потому что в предложении сказано «3000 долларов или меньше».
Давайте теперь попрактикуемся в некоторых из них.
Практика
1. Какой символ означает меньше чем?
А)
Б)
В)
Г)
2. Какой символ означает больше или равно?
А)
Б)
В)
Г)
3. Какой символ означает меньше или равно?
А)
Б)
В)
Г)
4.Какой символ означает больше?
А)
Б)
В)
Г)
5.![]() Как бы вы написали «три больше нуля»?
Как бы вы написали «три больше нуля»?
А) 3 0
Б) 3 0
В) 3 0
Г) 3 0
6. Как бы вы написали «x меньше или равно 9»?
А) x 9
Б) х 9
В) х 9
D) x 9
7.Как бы вы написали «m плюс четыре меньше 6»?
А) м + 4 6
Б) м + 4 6
В) м + 4 6
Г) м + 4 6
Выберите эквивалентное неравенство.
Построить графическое изображение простых неравенств просто. В простом неравенстве слева переменная (x или другая буква), а справа число.
Для начала поставьте точку в числовой строке данного числа. Если символ неравенства — или, используйте обычную сплошную точку.Если символ неравенства — <или>, используйте пустую точку.
| Для или используйте. Для <или> используйте. |
Сначала поставьте точку на числовой прямой в точке числа справа от неравенства. Затем нарисуйте линию со стрелкой до упора вправо, если символ> или. Нарисуйте линию со стрелкой до упора влево, если символ <или.
Затем нарисуйте линию со стрелкой до упора вправо, если символ> или. Нарисуйте линию со стрелкой до упора влево, если символ <или.
Вы можете запомнить их, просто подумав, что означают символы.
означает больше числа (но не равно, поэтому точка пуста, поскольку само число не является частью ответа).
означает меньше числа (но не равно, поэтому точка пуста).
означает больше или равно числу (поэтому точка сплошная).
означает меньше или равно числу (поэтому точка сплошная).
Давайте рассмотрим несколько примеров, основанных на этих правилах.
График x> 3.
График x <-2.
График x 0.
График x -1.
Теперь вы попробуете.
Практика
Выберите правильный график для каждого неравенства.
12. х> -4
А)
Б)
В)
Г)
13. х 1
А)
Б)
В)
Г)
14. х <3
х <3
А)
Б)
В)
Г)
15.х> -1
А)
Б)
В)
Г)
16. х 6
А)
Б)
В)
Г)
17. Какое неравенство для этого графика правильное?
А) х -4
Б) х -4
В) х -4
Г) х -4
18. Какое неравенство для этого графика правильное?
А) x 3
Б) х 3
В) х 3
D) x 3
19.Какое неравенство правильное для этого графика?
А) x 6
Б) х 6
В) х 6
D) x 6
В неравенстве переменная (x или другая буква) является неизвестной. Чтобы решить неравенство, нам нужно найти значение переменной. Для этого мы получаем переменную, стоящую на одной стороне неравенства.
Мы должны сохранять баланс в уравнении, поэтому что бы мы ни делали с одной стороны уравнения, мы должны делать и с другой стороной .
Чтобы получить x сам по себе, мы используем обратные операции , чтобы избавиться от всего, что есть с x. Это означает, что мы поступаем наоборот. Если в уравнении к x добавлено , нам нужно вычесть , чтобы от него избавиться. Если что-то вычтено из x , нам нужно добавить , чтобы избавиться от этого. Помните, что все, что мы делаем с одной стороной, мы делаем и с другой стороной.
Вот пример. Решить x + 5> 9.
Мы можем изобразить это решение следующим образом:
Для каждого решаемого вами неравенства вы можете проверить свою работу, подставив свой ответ обратно в задачу, чтобы убедиться, что он правильный.В этом случае мы выберем для x значение> 4. Мы используем 5 и подставим это в исходное уравнение:
Мы видим, что 10 больше 9, и наш чек работает.
Давай сделаем еще один. Решите m — 3 0. Помните, что вам нужно использовать обратные операции, чтобы получить переменную отдельно.
Решите m — 3 0. Помните, что вам нужно использовать обратные операции, чтобы получить переменную отдельно.
График этого решения:
Давайте проверим наше решение, подставив число, которое больше или равно 3. Мы будем использовать 3.
Приведем еще один пример.Решите p + 6 <8.
Вот график решения:
Мы можем проверить наше решение, подставив значение меньше 2. Мы будем использовать 1.
Давайте посмотрим на неравенства, которые включают умножение и деление.
Опять же, нам нужно получить переменную на одной стороне неравенства отдельно. Чтобы сбалансировать уравнение, что бы мы ни делали с одной стороной уравнения, мы должны делать и с другой стороной.
Чтобы получить x сам по себе, мы используем обратные операции, чтобы избавиться от всего, что есть с x.Это означает, что мы поступаем наоборот. Если в уравнении что-то умножается на x, нам нужно разделить на это , чтобы избавиться от этого. Если x — это , деленное на что-то , нам нужно умножить на него , чтобы избавиться от него.
Единственным новым шагом является то, что , если мы умножаем или делим на отрицательное число, нам нужно перевернуть знак неравенства .
Приведем пример. Решить 6x> 12.
Вот график решения:
Давайте проверим нашу работу.Нам нужно подставить вместо x число больше 2. Мы будем использовать 3.
18 больше 12, поэтому наш чек хорош.
Поскольку эта задача не связана с умножением или делением на отрицательное число, нам не нужно менять знак неравенства.
Давай сделаем еще один. Здесь отрицательное число, поэтому нам нужно не забыть перевернуть знак неравенства. Решить –2t 10.
Вот график решения:
Давайте проверим нашу работу.Нам нужно заменить t на число, которое больше или равно -5. Давайте использовать -4.
Давайте сделаем еще один, в котором есть разделение.
Для этой задачи нам нужно будет умножить на –2, чтобы получить x само по себе, поэтому нам нужно поменять местами знак неравенства.
Вот график решения:
Давайте проверим нашу работу. Нам нужно подставить число вместо x, которое меньше -2. Давайте использовать -4.
А теперь давайте объединим все, что мы узнали.
Для решения некоторых неравенств требуется более одного шага. Например:
3x + 6 <27
Если у вас есть и умножение или деление, и сложение или вычитание, сначала отмените сложение или вычитание.
Давайте посмотрим на этот пример.
Здесь мы проверяем нашу работу, подставляя число вместо x, которое меньше 7. Мы будем использовать 6.
Давай сделаем еще один.
Помните, что всякий раз, когда мы делим или умножаем на отрицательное число, нам нужно перевернуть знак неравенства.
Здесь мы проверяем нашу работу, подставляя вместо x число меньше -18. Мы будем использовать -21.
Вот еще один пример.
Здесь мы проверяем нашу работу, подставляя вместо x число больше 1. Мы будем использовать 2.
Мы будем использовать 2.
Как набирать [клавиатура, Excel, Mac]
Как я могу ввести и использовать знак «не равно»?
1. Как сделать так, чтобы на клавиатуре знак «Не равно»?
Скопируйте знак неравенства из карты символов Windows
- Windows включает карту символов, из которой вы можете выбирать и копировать различные символы.Чтобы найти карту символов, нажмите сочетание клавиш Windows + S.
- Затем введите Таблица символов в поле «Введите здесь для поиска».
- Щелкните Таблица символов, чтобы открыть окно, показанное непосредственно ниже.
- Выберите Расширенный вид , чтобы открыть дополнительные параметры.
- Введите не равно в поле «Искать».
- Нажмите кнопку Выберите .
- Нажмите кнопку Копировать .
- Откройте документ, в который нужно добавить знак «не равно».

- Затем нажмите горячую клавишу Ctrl + V, чтобы вставить в документ знак «Не равно».
Google это
- Вы также можете погуглить знак «не равно». Откройте Google в браузере.
- Введите ключевое слово не равно в поле поиска Google.
- Вы увидите знак «не равно» в верхней части результатов поиска, как на изображении ниже.
- Удерживая левую кнопку мыши, перетащите курсор на знак «не равно», чтобы выбрать его.
- Нажмите горячую клавишу Ctrl + C .
- Чтобы удалить форматирование со знака, сначала вставьте его в Блокнот. Введите Notepad в поле поиска Windows 10.
- Щелкните Блокнот, чтобы открыть его.
- Нажмите горячую клавишу Ctrl + V , чтобы вставить туда знак. Затем скопируйте знак «не равно» в Блокнот с помощью Ctrl + C .
- Наконец, вставьте в документ знак «Не равно» с помощью сочетания клавиш Ctrl + V .

2. Как ввести знак «Не равно» на Mac?
Пользователи Mac могут вводить знак «Не равно» в документы, не копируя его. На клавиатуре Apple есть клавиша Option, которую пользователи могут нажимать в сочетании с другими для ввода символов и символов в документах. Нажмите сочетание клавиш Option + = Mac, чтобы ввести в документы символ «не равно».
4. Выберите в Word
символ «не равно».- Пользователи MS Word могут выбирать символы для добавления в документы.Чтобы добавить символ «не равно», щелкните вкладку «Вставка» в Word.
- Щелкните Символ , чтобы открыть набор символов.
- Выберите «» не соответствует значку « л».
3. Где в Excel находится оператор «Не равно»?
Пользователи Excel могут вводить знак «не равно» в ячейки электронной таблицы любым из вышеперечисленных методов. Однако ввод знаков неравенства для функций Microsoft Excel — это не одно и то же. Для этого пользователям необходимо ввести оператор <> для не равно на панели функций.
Для этого пользователям необходимо ввести оператор <> для не равно на панели функций.
В качестве примера выберите ячейку электронной таблицы Excel, чтобы включить функцию «Не равно». Затем щелкните на панели функций, введите = 7 <> 9 в строке и нажмите Return. В ячейке функции отобразится ИСТИНА, как показано ниже.
Однако в ячейке функции «Не равно» будет отображаться ЛОЖЬ, если ее значения совпадают. Вместо этого введите = 9 <> 9 на панели функций и нажмите клавишу возврата.Тогда вывод ячейки функции будет ЛОЖНЫМ, как на снимке экрана ниже.
Как видите, есть несколько различных способов ввести знак «не равно» в текстовый редактор или электронные таблицы.
Общие математические символы и терминология
Математические символы и терминология могут сбивать с толку и препятствовать изучению и пониманию основ математики.
Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.
Мы что-то упускаем? Дайте нам знать.
Общие математические символы
+ сложение, плюс, положительное
Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.
Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2. На нашей странице о положительных и отрицательных числах объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.
Подробнее см. На нашей странице Дополнение .
— вычитание, минус, отрицание
Этот символ имеет два основных применения в математике:
- — используется, когда нужно вычесть одно или несколько чисел, например, 2 — 2.
- Символ — также обычно используется для обозначения отрицательного или отрицательного числа, например −2.

Подробнее см. Нашу страницу о Вычитание .
× или * или. Умножение
Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.
Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.
Реже умножение также может быть обозначено точкой.или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) совпадает с 2 × (3 + 2).
См. Дополнительную информацию на нашей странице Умножение .
÷ или / Подразделение
Оба эти символа используются для обозначения деления в математике. ÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
/ используется в электронных таблицах и других компьютерных приложениях.
Подробнее см. На нашей странице в Division .
= равно
Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычисления, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.
Вы также можете встретить другие похожие символы, хотя они встречаются реже:
- ≠ означает не равно.Например, 2 + 2 ≠ 5 — 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
- ≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.

- ≈ означает примерно равно или почти равно. Две стороны отношения, обозначенные этим символом, будут , а не достаточно точными для математических манипуляций.
<Меньше и> Больше
Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.
Этот символ > означает больше, например, 4> 2.
≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и> =.
≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.
± плюс или минус
Этот символ ± означает «плюс или минус». Он используется для обозначения, например, доверительных интервалов вокруг числа.
Считается, что ответ — это «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.
Например, 5 ± 2 на практике может быть любым числом от 3 до 7.
∑ Сумма
Символ ∑ означает сумму.
∑ — заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — кнопка Автосумма имеет сигму в качестве значка.
° Степень
Градусы ° используются по-разному.
- В качестве меры поворота — угол между сторонами фигуры или поворот круга. Круг равен 360 °, а прямой угол — 90 °. См. Наш раздел о Geometry для получения дополнительной информации.
- Мера температуры. градусов Цельсия или Цельсия используются в большинстве стран мира (за исключением США).Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется Фаренгейт. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F.
 Смотрите нашу страницу: Системы измерения для получения дополнительной информации.
Смотрите нашу страницу: Системы измерения для получения дополнительной информации.
∠ Угол
Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.
Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Аналогичным образом, ∠BAC может использоваться для описания угла точки A (между точками B и C).Подробнее об углах и других геометрических терминах см. На наших страницах Geometry .
√ Квадратный корень
√ — символ квадратного корня. Квадратный корень — это число, которое при умножении на себя дает исходное число.
Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.
См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.
n Мощность
Целое число с верхним индексом (любое целое число n ) — это символ, используемый для обозначения степени числа.
Например, 3 2 означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).
4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.
См. Наши страницы Расчетная площадь и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .
Степени также используются как сокращенный способ записи больших и малых чисел.
Большие числа
10 6 — 1 000 000 (один миллион).
10 9 — 1 000 000 000 (один миллиард).
10 12 — 1 000 000 000 000 (один триллион).
10 100 , написанное длинной рукой, будет равно 1 с 100 нулями (один гугол).
Маленькие числа
10 -3 — 0,001 (одна тысячная)
10 -6 равно 0.6 = 10 6 = 1000000 (один миллион).
. Десятичная точка
. — символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.
, Разделитель тысяч
Запятую можно использовать для разделения больших чисел и облегчения их чтения.
Тысячу можно записать как 1000, так и 1000, а миллион — как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.
В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.
В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и, действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя.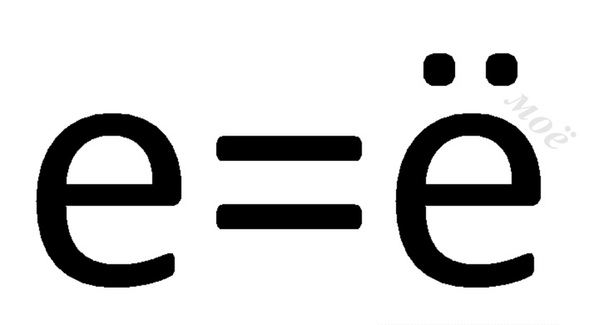 Это объясняется более подробно на нашей странице Introduction to Numbers .
Это объясняется более подробно на нашей странице Introduction to Numbers .
[], () Скобки, круглые скобки
Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.
Сначала вычисляются части расчета, заключенные в скобки, например
.- 5 + 3 × 2 = 11
- (5 + 3) × 2 = 16
% В процентах
Символ% означает процент или число из 100.
Узнайте все о процентах на нашей странице: Введение в проценты
π Pi
π или пи — греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи — это длина окружности, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.
∞ Бесконечность
Символ ∞ означает бесконечность — понятие, согласно которому числа существуют вечно.
Каким бы большим у вас ни было число, вы всегда можете выбрать номер побольше, потому что вы всегда можете добавить к нему единицу.
Бесконечность — это не число, а идея чисел , существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, к любви или ненависти.
\ (\ bar x \) (x-bar) Среднее значение
\ (\ bar x \) — это среднее значение всех возможных значений x.
Чаще всего этот символ встречается в статистике.
Дополнительную информацию см. На нашей странице Среднее значение .
! Факториал
! это символ факториала.
н! — произведение (умножение) всех чисел от n до 1 включительно, то есть n × (n − 1) × (n − 2) ×… × 2 × 1.
Например:
5! = 5 × 4 × 3 × 2 × 1 = 120
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800
| Труба
Труба ‘|’ также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.
Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) — это абсолютное значение или модуль \ (x \) .
Математически это определяется как
$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$
Проще говоря, \ (\ vert x \ vert \) — неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.
Он также используется в вероятности, где P (Z | Y) обозначает вероятность X при условии Y.
∝ Пропорциональный
∝ означает «пропорционально » и используется, чтобы показать что-то, что меняется по отношению к другому.
Например, если x = 2y, то x ∝ y.
∴ Следовательно
∴ — это удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.
∵ Потому что
∵ — удобная сокращенная форма слова «потому что», не путать с «поэтому».
Математическая терминология (A-Z)
Амплитуда
Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда — это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.
Апофема
Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.
Площадь
Геометрическая площадь — это пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах ( м 2 ).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .
Площадь измеряется в квадратных единицах, например в квадратных метрах ( м 2 ).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .
Асимптота
Асимптота — это прямая линия или ось, которая конкретно связана с кривой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Это происходит в геометрии и тригонометрии .
ось
Опорная линия, относительно которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.
Коэффициент
Коэффициент — это число или величина, умножающая другую величину. Обычно он помещается перед переменной . В выражении 6 x , 6 — коэффициент, а x — переменная.
Окружность
Окружность — это длина расстояния по краю круга. Это тип периметра , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу о изогнутых форм .
Данные
Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум — это одно значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.
Диаметр
Диаметр — это термин, используемый в геометрии для определения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза превышает радиус .
Экстраполировать
Экстраполяция — это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.
Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.
Фактор
Коэффициент — это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное количество факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя — себя и 1. Простой множитель — множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 — простые числа).
Среднее значение, медиана и мода
Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, среднее значение составляет . Режим — это число, которое встречается чаще всего.
Режим — это число, которое встречается чаще всего.
Операция
Математическая операция — это шаг или этап в вычислении или математическое «действие». Основные арифметические операции — это сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .
Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.
Периметр
Периметр 2-мерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница на Perimeter объясняет это более подробно.
Пропорции
Пропорция — это относительное отношение. Соотношения сравнивают одну часть с другой частью, а пропорции сравнивают одну часть с целым.![]() Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к фракциям .
Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к фракциям .
Пифагор
Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .
Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».
Количественный и качественный
Количественные данные представляют собой числовые переменные или значения, которые могут быть выражены численно, т.е. сколько, сколько, как часто, и получаются путем подсчета или измерения.
Качественные данные — это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.
Подробнее см. Нашу страницу о типах данных .
Радиан
Радиан — это единица измерения угла в системе СИ. Один радиан эквивалентен углу, образуемому в центре окружности дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.
Радиус
Термин радиус используется в контексте кругов и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до ее внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Для получения дополнительной информации см. Нашу страницу о изогнутых форм .
Диапазон
В статистике диапазон данного набора данных — это разница между наибольшим и наименьшим значениями.
Коэффициент
Коэффициент — это математический термин, используемый для сравнения размеров одной детали с другой. Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.
Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.
Стандартное отклонение
Стандартное отклонение набора данных показывает, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные распределены в более широком диапазоне
Срок
Термин — это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).
переменная
Переменная — это коэффициент , коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, который может изменяться. В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , а x — переменная.
В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , а x — переменная.
Разница
Дисперсия — это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе от среднего и, следовательно, от каждого другого члена в наборе.
Вектор
Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например изучение движения, где скорость, ускорение, сила, перемещение и импульс являются векторными величинами.
Объем
Объем — это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическим измерением пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м 3 .
Уравнения и неравенства — Неравенства
Решение неравенство очень похоже на решение уравнения.Вы следуете тем же шагам, кроме одного очень важного отличия. Когда вы умножаете или делите каждый сторону неравенства на отрицательное число, необходимо обратить неравенство символ! Давайте попробуем пример:
-4x > 24
С этого момента неравенство предполагает умножение, мы должны использовать обратное или деление, чтобы решить это. Мы разделим обе части на –4, чтобы оставить x в покое. с левой стороны.
Когда мы упрощаем, поскольку мы делим на отрицательное число, мы должны не забыть перевернуть символ. Это дает «x меньше –6», а не «x равно больше –6. «
х <-6
Почему мы
перевернуть символ? Посмотрим, что будет, если мы этого не сделаем. Подумайте о
простое неравенство –3 <9. Это, очевидно, верное утверждение.
Подумайте о
простое неравенство –3 <9. Это, очевидно, верное утверждение.
-3 <9
Для демонстрации что происходит, когда мы делим на отрицательное число, давайте разделим обе стороны на –3.Если мы оставим символ неравенства прежним, наш ответ, очевидно, будет неверно, так как 1 не меньше –3.
Мы должны перевернуть символ, чтобы найти правильный ответ: «1 больше –3».
Вернемся назад к исходной задаче и изобразить решение x <–6 на число линия. Чтобы построить график решения неравенства, вы начинаете с определения точка в неравенстве.Здесь –6. Затем вы наносите на график все точки которые находятся в решении.
Красная стрелка показывает, что все значения в числовой строке меньше –6 находятся в решение. Белый кружок на –6 показывает нам, что –6 не входит в число решение. Если бы решение было «x меньше или равно –6», круг будет темным или закрашенным.
Как мы можем проверить наш ответ? Мы не можем использовать –6 для замены в неравенстве, потому что он лежит за пределами нашего решения.Для проверки мы можем выбрать любое значение это кроется в решении. Давайте использовать –7.
-4x
> 24
-4 (-7)> 24
28> 24 Правильно!
Наша замена дал верный результат, значит, решение верное.
назад наверх
Как использовать символ «Google Таблицы не равно»?
Google Таблицы не равно — это символ <>, который является логическим оператором, используемым для сравнения двух значений.С логическими операторами вы, вероятно, уже хорошо знакомы (возможно, вы просто этого не знаете). Обсуждая логические операторы вне программирования, мы обычно имеем в виду меньше «<», больше «>» и равняются «=». Напоминаем, что все логические операторы дают логическое значение ИСТИНА или ЛОЖЬ
Пример. На 5 яблок меньше «<» 10 яблок. Все мы знаем, что это ИСТИНА , поскольку 5 меньше 10.
В языках программирования у нас также есть логические операторы, но есть несколько более сложных, к которым нужно немного привыкнуть.Тот, который мы рассматриваем сегодня, известен как , «не равно» .
Логическая концепция «не равно»
«Не равно» по своей сути является просто противоположной оценкой равного. Концептуально это означает следующее:
Если два значения оцениваются с использованием EQUALS и возвращают TRUE , то те же два значения, вычисленные с помощью NOT EQUALS , вернут FALSE . Обратный оператор работает таким же образом с NOT EQUALS, что дает значение OPPOSITE.
- Если вычисление A «равно» A , возвращается к ИСТИНА
- При вычислении A «не равно» A возвращает FALSE
Если два значения оцениваются с использованием EQUALS и вернет FALSE , тогда те же два значения, вычисленные с помощью NOT EQUALS , вернут TRUE .
- Если оценка A «равно» B , возвращается к FALSE
- Оценка A «не равно» B , возвращает TRUE
Опять же, чтобы сделать это как можно проще, если равно оценивает ИСТИНА не равно будет оценивать ЛОЖЬ, всегда наоборот.Именно по этой причине в большинстве других языков «не равно» на самом деле является составным символом! =, Где «!» означает НЕ или ПРОТИВОПОЛОЖЕНИЕ, а «=» означает равно. Как вы можете себе представить, этот составной символ! = Означает противоположность равных.
Примеры того, когда использовать «Не равно»
По моему опыту, наиболее распространенный вариант использования «Не равно» — это когда вы имеете дело с фильтрацией списков вещей или сравнением со списком элементов. Не равно хорошо работает и со списками, которые меняются со временем.Представьте себе следующий сценарий:
Google Таблицы не равны — Пример студенческого округаДопустим, у вас есть список учащихся и округов, в которых они находятся. Энни и Боб находятся в округе 1, Чарли и Дэйв — в округе 2, а Эван и Фиона — в округе 3. Теперь вы. хотите узнать, кто НЕ входит в округ 3.
Если бы у нас не было логического оператора «не равно» , нам пришлось бы записать это как округ = 1 ИЛИ округ = 2 чтобы получить ответ. Давайте перенесемся в будущее, и мы хотим добавить еще 97 районов из 100 районов? Нам нужно будет добавить операторы ИЛИ для каждого нового добавленного округа: округ = 1, ИЛИ округ = 2, ИЛИ….. District = 100, чтобы получить всех, кто НЕ в округе 3. Конечно, это ужасное использование времени и пространства, верно?
К счастью, мы используем оператор «не равно» вместо того, чтобы писать все эти ИЛИ. При использовании округа «не равно» 3 не имеет значения, сколько еще округов есть, ИЛИ, если позже будет добавлено больше округов, ваша формула все еще работает.
Google Sheets Not Equal
В Google Sheets символ «Не равно» — это <>, например, A <> B = TRUE.



 Затем полученное число округляется до ближайшего возможного значения типа
Затем полученное число округляется до ближайшего возможного значения типа 
 Может использоваться со строками (сравнение основывается на алфавитном порядке) и для числовых вычислений, а также дат.
Может использоваться со строками (сравнение основывается на алфавитном порядке) и для числовых вычислений, а также дат. Если перед NULL стоит NOT, выбирает запись, где в определенном поле есть какое-то значение.
Если перед NULL стоит NOT, выбирает запись, где в определенном поле есть какое-то значение.
 Аргумент extract_source является выражением даты–времени. Аргументом extract_field может быть одно из следующих ключевых слов: YEAR, MONTH, DAY, HOUR, MINUTE или SECOND.
Аргумент extract_source является выражением даты–времени. Аргументом extract_field может быть одно из следующих ключевых слов: YEAR, MONTH, DAY, HOUR, MINUTE или SECOND.





 В текущей версии Ruby они называются регулярными выражениями, но давайте смотреть в будущее. Perl 6 уже не имеет понятия «регулярное выражение», заменив его «правилами» и «грамматиками».
В текущей версии Ruby они называются регулярными выражениями, но давайте смотреть в будущее. Perl 6 уже не имеет понятия «регулярное выражение», заменив его «правилами» и «грамматиками». ."z"
"a"..."z" # то же, что и "a".."y"
1..100
1...100 # то же, что и 1..99
."z"
"a"..."z" # то же, что и "a".."y"
1..100
1...100 # то же, что и 1..99