Цифры и символы: Таблица символов Юникода (Unicode) для сайта: цифры, смайлики, спец символы

Таблица символов Юникода (Unicode) для сайта: цифры, смайлики, спец символы

На выдаче в сниппете и Title могут отображаться специализированные символы, знаки, буквы и цифры. Использовать их можно для оригинального оформления SEO-блоков. Только следует учитывать, что применение символов и необычных знаков должно быть продуманным и обоснованным. Иначе сниппет или тайтл может выглядеть нелепо, совершенно не справляясь с поставленными задачами. Поисковые системы по-разному реагируют на использование символов, смайликов, стрелочек, необычных знаков. Рекомендуем протестировать их, чтобы убедиться в правильности отображения в выдаче.

Как использовать Unicode символы

• Найти нужный значок;
• Скопировать его;
• Вставить в нужное место в тексте.

Наиболее популярные символы

Чаще всего для выдачи применяют символы рубля и валют, серп и молот, а также инь и янь.

® ✉ § © ☯ ☭ ? $ £ ¢

Российский рубль: U+20BD (в Юникоде) и ₽ (в HTML-коде)

Нумерация, буквы, числа в Юникод

Используемые варианты:

• ⓿ ❶ ❷ ❸ ❹ ❺ ❻ ❼ ❽ ❾ ❿ ⓫ ⓬ ⓭ ⓮ ⓯ ⓰ ⓱ ⓲ ⓳ ⓴
• ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽ ⑾ ⑿ ⒀ ⒁ ⒂ ⒃ ⒄ ⒅ ⒆ ⒇
• ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ⑪ ⑫ ⑬ ⑭ ⑮ ⑯ ⑰ ⑱ ⑲ ⑳
• Ⓐ Ⓑ Ⓒ Ⓓ Ⓔ Ⓕ Ⓖ Ⓗ Ⓘ Ⓙ Ⓚ Ⓛ Ⓜ Ⓝ Ⓞ Ⓟ Ⓠ Ⓡ Ⓢ Ⓣ Ⓤ Ⓥ Ⓦ Ⓧ Ⓨ Ⓩ
• ⒈ ⒉ ⒊ ⒋ ⒌ ⒍ ⒎ ⒏ ⒐ ⒑ ⒒ ⒓ ⒔ ⒕ ⒖ ⒗ ⒘ ⒙ ⒚ ⒛
• ⓐ ⓑ ⓒ ⓓ ⓔ ⓕ ⓖ ⓗ ⓘ ⓙ ⓚ ⓛ ⓜ ⓝ ⓞ ⓟ ⓠ ⓡ ⓢ ⓣ ⓤ ⓥ ⓦ ⓧ ⓨ ⓩ ⓪
• ⒜ ⒝ ⒞ ⒟ ⒠ ⒡ ⒢ ⒣ ⒤ ⒥ ⒦ ⒧ ⒨ ⒩ ⒪ ⒫ ⒬ ⒭ ⒮ ⒯ ⒰ ⒱ ⒲ ⒳ ⒴ ⒵

Колбочки, стрелочки, квадратики

Основные варианты:

• ◜ ◝ ◞ ◟ ◠ ◡
• ◰ ◱ ◲ ◳ ◴ ◵ ◶ ◷
• ▖ ▗ ▘ ▙ ▚ ▛ ▜ ▝ ▞ ▟ ■
• ◸ ◹ ◺ ◻ ◼ ◽ ◾ ◿
• ► ▻ ▼ ▽ ▾ ▿ ◀ ◁ ◂ ▻
• □ ▢ ▣ ▪ ▫ ▬ ▭ ▮ ▯ ▰ ▱ ▤ ▥ ▦ ▧ ▨ ▩
• ▲ △ ▴ ▵ ▶ ▷ ▸ ▹ ► ▻
• ◢ ◣ ◤ ◥
• ◆ ◇ ◈ ◉ ◊ ○ ◌ ◍ ◎
• ● ◐ ◑ ◒ ◓ ◔ ◕
• ◧ ◨ ◩ ◪ ◫
• ◖ ◗ ◘ ◙ ◚ ◛
• ◦ ◬ ◭ ◮ ◯

Крестики, черточки, палочки в UNICODE

Используемые символы:

• ▁ ▂ ▃ ▄ ▅ ▆ ▇ █
• ▌ ▍ ▎ ▏ ▐
• ▀ ▉ ▊ ▋
• ─ ━ │ ┃
• └ ┕ ┖ ┗ ┘ ┙ ┚ ┛
• ┄ ┅ ┆ ┇ ┈ ┉ ┊ ┋
• ░ ▒ ▓ ▔ ▕
• ┌ ┍ ┎ ┏ ┐ ┑ ┒ ┓
• ╭ ╮ ╯ ╰ ╱ ╲ ╳
• ├ ┝ ┞ ┟ ┠ ┡ ┢ ┣ ┤ ┥ ┦ ┧ ┨ ┩ ┪ ┫
• ╴ ╵ ╶ ╷ ╸ ╹ ╺ ╻ ╼ ╽ ╾ ╿
• ┴ ┵ ┶ ┷ ┸ ┹ ┺ ┻
• ┬ ┭ ┮ ┯ ┰ ┱ ┲ ┳
• ┼ ┽ ┾ ┿ ╀ ╁ ╂ ╃ ╄ ╅ ╆ ╇ ╈ ╉ ╊ ╋
• ╤ ╥ ╦ ╧ ╨ ╩ ╪ ╫ ╬
• ╘ ╙ ╚ ╛ ╜ ╝
• ╌ ╍ ╎ ╏ ═
• ║ ╞ ╟ ╠ ╡ ╢ ╣
• ╒ ╓ ╔ ╕ ╖ ╗

Фигурные символы

Используются специальные символы:

• ⟨ ⟩ ⟪ ⟫ ⟰ ⟱
• ❍ ❏ ❐ ❑ ❒
• ✔ ✕ ✖ ✗ ✘
• ☀ ☁ ☂ ☃ 🤘 ☄ ★ 💪
• ☢ ☣ ☯ ☮ ☣ ☬ ☪
• ☆ ☇ ☈ ☉ ☊ ☋ ☌ ☍
• ☡ ☢ ☣ ☤ ☥ ☧ ☨ ☩ ☪
• ☎ ☏ ☐ ☑ ☒
• ⟦ ⟧ ⟲ ⟳ ⟴ ⟵
• ➘ ➙ ➚ ➛ ➜ ➝ ➞ ➟ ➠ ➡
• ☓ ☔ ☕ ☖ ☗ ☘ ☙
 
• ☚ ☛ ☜ ☝ ☞ ☟ ☠ ☫ ☬
• ✆ ✇ ✈ ✉ ✌ ✍ ✎ ✏ ✐ ✑
• ➲ ➳ ➴ ➵ ➶ ➷ ➸
• ☰ ☱ ☲ ☳ ☴ ☵ ☶ ☷
• ☭ ☮ ☯  ♮ ♯ ♰ ♱
• ➱ ➢ ➣ ➤ ➥ ➦ ➧ ➨ ➩ ➪ ➫ ➬ ➭ ➮ ➯ ➔
• ❁ ❂ ❃ ❄ ❅ ❆ ❇ ❈ ❉ ❊ ❋
• ✁ ✂ ✃ ✄ ✒ ✓ ☦
• ✫ ✬ ✭ ✮ ✯ ✰
• ✝ ✞ ✟ ✠ ✡✢ ✣ ✤ ✥
• ✡ 〄 ♨ ☸ ⌘
• ✱ ✲ ✳ ✴ ✵ ✶ ✷ ✸ ✹ ✺ ✻ ✼ ✽ ❀
• ✙ ✚ ✛ ✾ ✿ ✜ ✦ ✧ ✩ ✪
• ➹ ➺ ➻ ➼ ➽ ➾
• ❖ ❡ ❢ ❣ ❤ ❥ ❦ ❧ ❘ ❙ ❚ ❛ ❜ ❝ ❞ 👌 ➿ ⟠ ⟡
 

Римские числа

ⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ ⅺ ⅻ ⅼ Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ Ⅼ

Шахматные фигуры и ноты

Используются следующие символы:

• ♕ ♖ ♗ ♘ ♙ ♚ ♛ ♜ ♝ ♞ ♟ ♠
• ♩ ♪ ♫ ♬ ♭ ♮ ♯
• ♡ ♢ ♣ ♤ ♥ ♦ ♧

Математические  символы  и  обозначения  в  физике  по  UNICODE

ℂ ℃ ℄ ℅ ℆ ℇ ℈ ℉ ℊ ℋ ℌ ℍ ℎ ℏ ℐ ℑ ℒ ℓ ℔ ℕ ℗ ℘ ℙ ℚ ℛ ℜ ℝ ℞ ℟ ℠ ℡ ™ ℣ ℤ ℥ Ω ℧ ℨ ℩ K Å № ℬ ℭ ℮ ℯ ℰ ℱ Ⅎ ℳ ℴ ⅓ ⅔ ⅕ ⅖ ⅗ ⅘ ⅙ ⅚ ⅛ ⅜ ⅝ ⅞ ⅟ ℵ ℶ ℷ ℸ ℹ ℺ ℻ ℽ ℾ ℿ ⅀ ⅁ ⅂ ⅃ ⅄ ⅅ ⅆ ⅇ ⅈ ⅉ ⅊ ⅋ ⅍ ⅎ Ⅽ Ⅾ Ⅿ∀ ∁ ∂ ∃ ∄ ∅ ∆ ∇ ∈ ∉ ∊ ∋ ∌ ∍ ∎ ∏ ∐ ∑ − ∓ ∔ ∕ ∖ ∗ ∘ ∙ √ ∛ ∜ ∝ ∞ ∟ ∠ ∡ ∢ ∣ ∤ ∥ ∦ ∧ ∨ ∩ ∪ ∫ ∬ ∭ ∮ ∯ ∰ ∱ ∲ ∳ ∴ ∵ ∶ ∷ ∸ ∹ ∺ ∻ ∼ ∽ ∾ ∿ ≀ ≁ ≂ ≃ ≄ ≅ ≆ ≇ ≈ ≉ ≊ ≋ ≌ ≍ ≎ ≏ ≐ ≑ ≒ ≓ ≔ ≕ ≖ ≗ ≘ ≙ ≚ ≛ ≜ ≝ ≞ ≟ ≠ ≡ ≢ ≣ ≤ ≥ ≦ ≧ ≨ ≩ ≪ ≫ ≬ ≭ ≮ ≯ ≰ ≱ ≲ ≳ ≴ ≵ ≶ ≷ ≸ ≹ ≺ ≻ ≼ ≽ ≾ ≿ ⊀ ⊁ ⊂ ⊃ ⊄ ⊅ ⊆ ⊇ ⊈ ⊉ ⊊ ⊋ ⊌ ⊍ ⊎ ⋐ ⋑ ⋒ ⋓ ⋔ ⋕ ⋖ ⋗ ⋘ ⋙ ⋚ ⋛ ⋜ ⋝ ⋞ ⋟ ⋠ ⋡ ⋢ ⋣ ⋤ ⋥ ⋦ ⋧ ⋨ ⋩ ⋪ ⋫ ⋬ ⋭ ⋮ ⋯ ⋰ ⋱ ⋲ ⋳ ⋴ ⋵ ⋶ ⋷ ⋸ ⋹ ⋺ ⋻ ⋼ ⋽ ⋾ ⋿ ⌀

Греческие буквы и другие алфавиты

ᴀ ᴁ ᴂ ᴃ ᴄ ᴅ ᴆ ᴇ ᴈ ᴉ ᴊ ᴋ ᴌ ᴍ ᴎ ᴏ ᴐ ᴑ ᴒ ᴓ ᴔ ᴕ ᴖ ᴗ ᴘ ᴙ ᴚ ᴛ ᴜ ᴝ ᴞ ᴟ ᴠ ᴡ ᴢ ᴣ ᴤ ᴥ ᴦ ᴧ ᴨ ᴩ ᴪ ᴫ ᴬ ᴭ ᴮ ᴯ ᴰ ᴱ ᴲ ᴳ ᴴ ᴵ ᴶ ᴷ ᴸ ᴹ ᴺ ᴻ ᴼ ᴽ ᴾ ᴿ ᵀ ᵁ ᵂ ᵃ ᵄ ᵅ ᵆ ᵇ ᵈ ᵉ ᵊ ᵋ ᵌ ᵍ ᵎ ᵏ ᵐ ᵑ ᵒ ᵓ ᵔ ᵕ ᵖ ᵗ ᵘ ᵙ ᵚ ᵛ ᵜ ᵝ ᵞ ᵟ ᵠ ᵡ ᵢ ᵣ ᵤ ᵥ ᵦ ᵧ ᵨ ᵩ ᵪ ᵫ ᵬ ᵭ ᵮ ᵯ ᵰ ᵱ ᵲ ᵳ ᵴ ᵵ ᵶ ᵷ ᵸ ᵹ ᵺ ᵻ ᵼ ᵽ ᵾ ᵿ ᶀ ᶁ ᶂ ᶃ ᶄ ᶅ ᶆ ᶇ ᶈ ᶉ ᶊ ᶋ ᶌ ᶍ ᶎ ᶏ ᶐ ᶑ ᶒ ᶓ ᶔ ᶕ ᶖ ᶗ ᶘ ᶙ ᶚ ᶛ ᶜ ᶝ ᶞ ᶟ ᶠ ᶡ ᶢ ᶣ ᶤ ᶥ ᶦ ᶧ ᶨ ᶩ ᶪ ᶫ ᶬ ᶭ ᶮ ᶯ ᶰ ᶱ ᶲ ᶳ ᶴ ᶵ ᶶ ᶷ ᶸ ᶹ ᶺ ᶻ ᶼ ᶽ ᶾ ᶿ ῲ ῳ ῴ ῶ ῷ Ὸ Ό Ὼ Ώ ῼ ⍳ ⍴ ⍵ ⍶ ⍷ ⍸ ⍹ ⍺

Нестандартная символика

← ↑ → ↓ ↔ ↕ ↖ ↗ ↘ ↙ ↚ ↛ ↜ ↝ ↞ ↟ ↠ ↡ ↢ ↣ ↤ ↥ ↦ ↧ ↨ ↩ ↪ ↫ ↬ ↭ ↮ ↯ ↰ ↱ ↲ ↳ ↴ ↵ ↶ ↷ ↸ ↹ ↺ ↻ ↼ ↽ ↾ ↿ ⇀ ⇁ ⇂ ⇃ ⇄ ⇅ ⇆ ⇇ ⇈ ⇉ ⇊ ⇋ ⇌ ⇍ ⇎ ⇏ ⇐ ⇑ ⇒ ⇓ ⇔ ⇕ ⇖ ⇗ ⇘ ⇙ ⇚ ⇛ ⇜ ⇝ ⇞ ⇟ ⇠ ⇡ ⇢ ⇣ ⇤ ⇥ ⇦ ⇧ ⇨ ⇩ ⇪ ⇫ ⇬ ⇭ ⇮ ⇯ ⇰ ⇱ ⇲ ⇳ ⇴ ⇵ ⇶ ⇷ ⇸ ⇹ ⇺ ⇻ ⇼ ⇽ ⇾ ⇿ ⊲ ⊳ ⊴ ⊵ ⊶ ⊷ ⊸ ⊹ ⊺ ⊻ ⊼ ⊽ ⊾ ⊿ ⋀ ⋁ ⋂ ⋃ ⋄ ⋅ ⋆ ⋇ ⋈ ⋉ ⋊ ⋋ ⋌ ⋍ ⋎ ⋏ ⌁ ⌂ ⌃ ⌄ ⌅ ⌆ ⌇ ⌈ ⌉ ⌊ ⌋ ⌌ ⌍ ⌎ ⌏ ⌐ ⌑ ⌒ ⌓ ⌔ ⌕ ⌖ ⌗ ⌘ ⌙ ⌚ ⌛ ⌜ ⌝ ⌞ ⌟ ⌠ ⌡ ⌢ ⌣ ⌤ ⌥ ⌦ ⌧ ⏎ ⏏ ⟶ ⟷ ⟸ ⟹ ⟺ ⟻ ⟼ ⟽ ⟾ ⟿ ⤀ ⤁ ⤂ ⤃ ⤄ ⤅ ⤆ ⤇ ⤈ ⤉ ⤊ ⤋ ⤌ ⤍ ⤎ ⤏ ⤐ ⤑ ⤒ ⤓ ⤔ ⤕ ⤖ ⤗ ⤘ ⤙ ⤚ ⤛ ⤜ ⤝ ⤞ ⤟ ⤠ ⤡

Цветные иконки и смайлики

😀 😃 😄 😁 😆 😅 🤣 😂 🙂 🙃 😉 😊 😇 🥰 😍 🤩 😘 😗 ☺ 😚 😙 😋 😛 😜 🤪 😝 🤑 🤗 🤭 🤫 🤔 🤐 🤨 😐 😑 😶 😏 😒 🙄 😬 🤥 😌 😔 😪 🤤 😴 😷 🤒 🤕 🤢 🤮 🤧 🥵 🥶 🥴 😵 🤯 🤠 🥳 😎 🤓 🧐 😕 😟 🙁 ☹ 😮 😯 😲 😳 🥺 😦 😧 😨 😰 😥 😢 😭 😱 😖 😣 😞 😓 😩 😫 😤 😡 😠 🤬 😈 👿 💀 ☠ 💩 🤡 👹 👺 👻 👽 👾 🤖 😺 😸 😹 😻 😼 😽 🙀 😿 😾 🙈 🙉 🙊 👋 🤚 🖐 ✋ 🖖 👌 ✌ 🤞 🤟 🤘 🤙 👈 👉 👆 🖕 👇 ☝ 👍 👎 ✊ 👊 🤛 🤜 👏 🙌 👐 🤲 🤝 🙏 ✍ 💅 🤳 💪 🦵 🦶 👂 👃 🧠 🦷 🦴 👀 👁 👅 👄 👶 🧒 👦 👧 🧑 👱 👨 🧔 👩 🧓 👴 👵 🙍 🙎 🙅 🙆 💁 🙋 🙇 🤦 🤷 👮 🕵 💂 👷 🤴 👸 👳 👲 🧕 🤵 👰 🤰 🤱 👼 🎅 🤶 🧙 🧚 🧛 🧜 🧝 🧞 🧟 💆 💇 🚶 🏃 💃 🕺 🕴 👯 🧖 🧗 🤺 🏇 ⛷ 🏂 🏌 🏄 🚣 🏊 ⛹ 🏋 🚴 🚵 🤸 🤼 🤽 🤾 🤹 🧘 🛀 🛌 👭 👫 👬 💏 💑 👪 🗣 👤 👥 👣 👓 🕶 🥽 🥼 👔 👕 👖 🧣 🧤 🧥 🧦 👗 👘 👙 👚 👛 👜 👝 🛍 🎒 👞 👟 🥾 🥿 👠 👡 👢 👑 👒 🎩 🎓 🧢 ⛑ 📿 💄 💍 💎 🔇 🔈 🔉 🔊 📢 📣 📯 🔔 🔕 🥁 📱 📲 ☎ 📞 📟 📠 🔋 🔌 💻 🖥 🖨 ⌨ 🖱 🖲 💽 💾 💿 📀 🧮 🎬 📷 📸 🔍 🔎 🕯 💡 🔦 🏮 📔 📕 📖 📗 📘 📙 📚 📓 📒 📃 📜 📄 📰 🗞 📑 🔖 🏷 🧾 💹 ✉ 📧 📨 📩 📤 📥 📦 📫 📪 📬 📭 📮 🗳 ✏ ✒ 🖋 🖊 🖌 🖍 📝 💼 📁 📂 🗂 📅 📆 🗒 🗓 📇 📈 📉 📊 📋 📌 📍 📎 🖇 📏 📐 ✂ 🗃 🗄 🗑 🔒 🔓 🔏 🔐 🔑 🗝 🔨 ⛏ ⚒ 🛠 🗡 ⚔ 🔫 🏹 🛡 🔧 🔩 ⚙ 🗜 ⚖ 🔗 ⛓ 🧰 🧲 ⚗ 🧪 🧫 🧬 🔬 🔭 📡 💉 💊 🚪 🛏 🛋 🚽 🚿 🛁 🧴 🧷 🧹 🧺 🧻 🧼 🧽 🧯 🛒 🚬 ⚰ ⚱ 🗿 ⌛ ⏳ ⌚ ⏰ ⏱ ⏲ 🕰 🕛 🕧 🕐 🕜 🕑 🕝 🕒 🕞 🕓 🕟 🕔 🕠 🕕 🕡 🕖 🕢 🕗 🕣 🕘 🕤 🕙 🕥 🕚 🕦 ° 🌑 🌒 🌓 🌔 🌕 🌖 🌗 🌘 🌙 🌚 🌛 🌜 🌡 ☀ 🌝 🌞 ⭐ 🌟 🌠 ☁ ⛅ ⛈ 🌤 🌥 🌦 🌧 🌨 🌩 🌪 🌫 🌬 🌀 🌈 🌂 ☂ ☔ ⛱ ⚡ ❄ ☃ ⛄ ☄ 🔥 💧 🌊

Арабские цифры ① ❶ ⓵ ¼ 𝟙 𝟏 в разном начертании

Римские

Ⅰ – 1 ; ⅩⅠ — 11

Ⅱ – 2 ; ⅩⅡ — 12

Ⅲ – 3 ; ⅩⅢ — 13

Ⅳ – 4 ; ⅩⅣ — 14

Ⅴ – 5 ; ⅩⅤ — 15

Ⅵ – 6 ; ⅩⅥ — 16

Ⅶ – 7 ; ⅩⅦ — 17

Ⅷ – 8 ; ⅩⅧ — 18

Ⅸ – 9 ; ⅩⅨ — 19

Ⅹ – 10 ; ⅩⅩ — 20

Ⅽ – 50 ; ⅩⅩⅠ — 21

Ⅾ — 100

Ⅿ — 500

ↁ — 1000

ↂ – 10000

Соответствие арабских цифр

Арабские (арбская письменность) = Индийские (в письменности деванагари) = Арабские (понятные нам)

٠ = ० = 0

١ = १ = 1

٢ = २ = 2

٣ = ३ = 3

٤ = ४ = 4

٥ = ५ = 5

٦ = ६ = 6

٧ = ७ = 7

٨ = ८ = 8

٩ = ९ = 9

Данная страница содержит красивые арабские цифры, которые не напечатать с клавиатуры. Их можно скопировать и вставить туда, где нельзя изменить шрифт (в соц. сетях). Кроме цифр, которыми пользуются европейцы, тут есть и настоящие — те что применяют сами арабы. А для комплекта, пусть тут же полежат и римские цифры и индийские. Есть же не попросят, я надеюсь. Все они из Юникода, узнать про них подробнее вы сможете, забив их в поиск на сайте.

Немного истории. Считается, что арабская система счисления зародилась в Индии, примерно, в V веке. Хотя, возможно, что ещё раньше и в Вавилоне. Арабскими цифры называются потому, что в Европу пришли от арабов. Сначала, в мусульманскую часть Испании, а в X веке уже и папа римский Сильвестр II призывал забросить громоздкую латинскую запись. Серьёзным толчком к распространению арабских цифр стал перевод на латинский язык книги Аль-Хорезми «Об индийском счёте».

Индо-арабская система записи чисел является десятичной. Любое число составляется из 10 знаков. Юникод, кстати, использует шестнадцатеричные числа. Удобнее римской она потому, что позиционная. В таких системах, величина которую обозначает цифра зависит от её положения в числе. В числе 90 цифра 9 значит девяносто, а в числе 951 – девятьсот. В непозиционных системах расположение символа не играет такой роли. Римская Х означает десять и в числе XII и в числе MXC. Подобным непозиционным образом записывали числа многие народы. У греков и у славян некоторые буквы алфавита имели и цифровое значение.

Если для кого-то эти символы слишком большие, то маленькие цифры лежат рядом. Маленькие буквы тоже в наличии.

Таблица символов цифр: арабские, римские, греческие, иврит

В таблице ниже представлены числа от 1 до 100, записанные цифрами разных систем счислений: арабской, римской, греческой, индо-арабской и еврейской.

Название числа	Арабские цифры	Римские цифры	Греческие цифры	Индо-арабские цифры	Цифры на иврите
ноль	0			٠
один	1	I	α	١	א
два	2	II	β	٢	ב
три	3	III	γ	٣	ג
четыре	4	IV	δ	٤	ד
пять	5	V	ε	٥	ה
шесть	6	VI	ϝ или ϛ	٦	ו
семь	7	VII	ζ	٧	ז
восемь	8	VIII	η	٨	ח
девять	9	IX	θ	٩	ט
десять	10	X	ι	١٠	י
одиннадцать	11	XI	ια	١١	יא
двенадцать	12	XII	ιβ	١٢	יב
тринадцать	13	XIII	ιγ	١٣	יג
четырнадцать	14	XIV	ιδ	١٤	יד
пятнадцать	15	XV	ιε	١٥	טו
шестнадцать	16	XVI	ιϛ	١٦	טז
семнадцать	17	XVII	ιζ	١٧	יז
восемнадцать	18	XVIII	ιη	١٨	יח
девятнадцать	19	XIX	ιθ	١٩	יט
двадцать	20	XX	κ	٢٠	כ
тридцать	30	XXX	λ	٣٠	ל
сорок	40	XL	μ	٤٠	מ
пятьдесят	50	L	ν	٥٠	נ
шестьдесят	60	LX	ξ	٦٠	ס
семьдесят	70	LXX	ο	٧٠	ע
восемьдесят	80	LXXX	π	٨٠	פ
девяносто	90	XC	ϟ	٩٠	צ
сто	100	C	ρ	١٠٠	ק

microexcel. _` { | } ~ (33 символа)

Имя пользователя для входа в систему

• Пробелы, двоеточия и кавычки не допускаются.

• Оно не может состоять только из цифр, и поле нельзя оставлять незаполненным.

• Длина ограничивается 32 символами.

Пароль для входа в систему

• Максимально допустимая длина пароля для администраторов и супервайзера составляет 32 символа, тогда как для пользователей длина ограничивается 128 символами.

• В отношении типов символов, которые могут использоваться для задания пароля, никаких ограничений не установлено. В целях безопасности рекомендуется создавать пароли, содержащие буквы верхнего и нижнего регистров, цифры и другие символы. Чем большее число символов используется в пароле, тем более трудной является задача его подбора для посторонних лиц.

• В подразделе [Политика паролей] раздела [Расширенная безопасность] вы можете установить требование в отношении обязательного включения в пароль букв верхнего и нижнего регистров, цифр и других символов, а также минимально необходимое количество символов в пароле. _` { | } ~ (33 символа)

Имя пользователя для входа в систему

• Пробелы, двоеточия и кавычки не допускаются.

• Это поле не может оставаться пустым.

• Длина ограничивается 32 символами.

• В регистрационном имени администратора длиной до 8 символов должны содержаться нецифровые символы (т.е. символы, не являющиеся числами). Если же оно состоит только из цифр, то его длина должна составлять не менее 9 символов.

Пароль для входа в систему

• Максимально допустимая длина пароля для администраторов и супервайзера составляет 32 символа, тогда как для пользователей длина ограничивается 128 символами.

• В отношении типов символов, которые могут использоваться для задания пароля, никаких ограничений не установлено. В целях безопасности рекомендуется создавать пароли, содержащие буквы верхнего и нижнего регистров, цифры и другие символы. Чем большее число символов используется в пароле, тем более трудной является задача его подбора для посторонних лиц.

• В подразделе [Политика паролей] раздела [Расширенная безопасность] вы можете установить требование в отношении обязательного включения в пароль букв верхнего и нижнего регистров, цифр и других символов, а также минимально необходимое количество символов в пароле. Для получения сведений о формировании политики паролей см. Настройка функций расширенной безопасности.

Как написать символами и знаками на клавиатуре?

 

 

 

 

Иногда возникает желание или необходимость написать символами или написать знаками на компьютерной клавиатуре.

 

Например, захотелось написать имя символами, что бы быть немного оригинальным и не похожим на других. Написать текст символами можно с помощью боковой клавиатуры NumLock.

Так как же написать знаками с помощью клавиатуры?

Написать знаками с помощью боковой клавиатуры легко для этого нужно:

1.    Включить боковую цифровую клавиатуру. Для включения боковой цифровой клавиатуры нажимаем клавишу NumLock включаем боковую клавиатуру для набора обычных цифр.

2.     Ставим курсор в нужное место, туда, где будем писать символы, знаки, цифры и буквы.

3.   Зажимаем кнопку Alt на клавиатуре, набираем цифру или цифры на боковой клавиатуре, отпускаем Alt

4.    Готова, должен появиться определенный знак или символ.    

Написать символами можно имя на свой вкус, например, в контакте.

Написать символами можно знак евро € (Alt+0136)

Написать на клавиатуре параграф: § (Alt+0167)

Написать символами можно знак бесконечности: ∞ (Alt+8734)

Написать знак торговая марка: ™ (Alt+0153)

Написать знак градуса «°» (Alt+0176)

Написать знак копирайта: © (Alt+0169)

Знак плюс минус: ± (Alt+0177)

Знак название, которого я не знаю: ® (Alt+0174)

Также можно написать на клавиатуре легкие символы и знаки:
☺символ (Alt+1)
☻ символ (Alt+2)
♥ символ (Alt+3)

И конечно многое другое как описанным способом, так и копируя символы и знаки по адресу: Пуск — Программы — Стандартные — Служебные — Таблица символов.

Ну а как написать символ собака @ на клавиатуре знают все, ☺ зажимаем одновременно shift и цифру 2. (При этом должна быть английская раскладка клавиатуры)

Обозначения чисел

 Каждое число занимает очень важное место в жизни и что-обозначает. Так, например сейчас  вычислительная система используется во всех сферах жизнедеятельности. Её широко используют в составлении гороскопов, в которые верят многие люди, а в древнем мире люди верили в магическую силу чисел и относились к ним очень осторожно, мы считаем, что осторожность нужно проявлять и в наше время, ведь кто знает, что будет, может на числах держится весь мир. Давайте посмотрим чтоже всё таки обозначают они на самом деле.

ОБОЗНАЧЕНИЯ ЧИСЕЛ

 

 

Древний Египет. Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. (См. сводную таблицу обозначений чисел.) Чтобы записанные таким образом числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона. Так, например, с помощью коллективных символов и повторений уже введенных символов число 6789 в иероглифических обозначениях можно было бы записать как.

Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком, например, девять записывалось как вместо , а семьсот как вместо . В этой записи число 6789 имело вид , причем знаки более высокого порядка располагались справа, а не слева. Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.

Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителямМесопотамии.                                                                                                                                                                                                      .

Вавилон. Письменность шумеров является, по-видимому, столь же древней, как и письменность египтян. Развитие способов представления чисел в Месопотамской долине вначале шло так же, как и в долине Нила, но затем жители Междуречья ввели совершенно новый принцип. Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались на солнце или в печи. Эти записи оказались исключительно долговечными, а потому, в отличие от египетских папирусов, дошедших до нас в весьма малом числе экземпляров, в музеях мира хранятся десятки тысяч клинописных табличек. Однако жесткость материала, на котором жители Месопотамии делали записи, оказала глубокое влияние на развитие числовых обозначений. Через некоторое время после того, как Аккад завоевал шумеров, система счисления в Месопотамии стала шестидесятиричной, хотя сохранилось также и основание 10. Казавшееся правдоподобным предположение относительно того, почему выбор пал на число 60 как на основу вавилонской системы счисления, и утверждавшее, будто это связано с тем, что продолжительность земного года считалась равной 360 дням, не получило подтверждения. Ныне принято считать, что шестидесятиричная система была выбрана из метрологических соображений: число 60 имеет много делителей.

Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта (в раннешумерских табличках – небольшой полукруг) означала единицу; повторенный нужное число раз, этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый коллективный символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку, (в раннешумерских текстах – небольшой кружок).

Повторенный соответствующее число раз, этот знак служил для обозначения чисел 20, 30, 40 и 50. Принцип повторного использования знаков позволял, например, записать число 59 в виде , т.е. 5?10 + 9.

Но для записи чисел больше 59 древние вавилоняне впервые использовали новый принцип – одно из самых выдающихся достижений в развитии систем обозначений чисел – принцип позиционности, т. е. зависимости значения символа от его местоположения в записи числа. Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять уже ранее использованные символы, если они будут занимать в записи числа новое положение левее предыдущих символов. Так, один клиновидный знак мог использоваться для обозначения и 1, и 60, и 602, и 603, в зависимости от занимаемого им в записи числа положения, подобно тому, как единица в наших обозначениях используется в записях и 10, и 102, и 103, и в числе 1111. При обозначении чисел больше 60 знаки, выступающие в новом качестве, отличались от старых тем, что символы разбивались на «места», или «позиции», и единицы более высокого порядка располагались слева. При таком способе записи для обозначения сколь угодно больших чисел уже не нужно было других символов, кроме уже известных. Например, число 6789 можно было записать так: , т.е. 1?(60)2 + 53?(60) + 9. В Древнем Вавилоне, ок. 1650 до н.э., система счисления оставалась псевдопозиционной или лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной запятой, равно как и символа для обозначения отсутствующей позиции. Обозначал ли символ число 1?(60)2 + 1 или 1?(60)2 + 1?(60), приходилось догадываться из контекста. Однако в период правления селевкидов, ок. 300 до н.э., эта неоднозначность была устранена введением специального символа в виде двух небольших клиньев, помещаемого на пустующее место, т.е. обозначающего пустую позицию в записи числа. Таким образом, из системы счисления была устранена отмеченная выше неоднозначность. Например, символ означал число 3601, т.е. 1?(60)2 + 0?(60) + 1. В то же время не было найдено ни одной таблички с записью, в которой символ нуля находился бы в конце числа. Именно поэтому вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60. Тем не менее изобретение вавилонянами позиционной системы счисления с нулем представляло собой огромное достижение, по своему революционному значению для математики сопоставимое разве лишь с более поздней гипотезой Коперника в астрономии.

Символы для обозначения чисел на вавилонских глиняных табличках не столь точны, как символы для обозначения чисел на древнеегипетских папирусах, несмотря на то, что вавилоняне использовали позиционный принцип. В исключительных случаях вавилоняне применяли сокращенные формы записи, иногда – с новыми символами для обозначения чисел 100 и 1000, или использовали принципы умножения или вычитания. Однако превосходство разработанной в Месопотамии системы счисления отчетливо видно в обозначении дробей. Здесь не требовалось вводить новые символы. Как и в нашей собственной десятичной позиционной системе, в древневавилонской системе подразумевалось, что на первом месте справа от единиц стоят величины, кратные 1/60, на втором месте – величины кратные 1/602 и т.д. Привычное нам деление часа и углового или дугового градуса на 60 минут, а одной минуты – на 60 секунд берет начало от вавилонской системы счисления.

Древняя Греция. В Древней Греции имели хождение две основных системы счисления – аттическая (или геродианова) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова «пента» (пять) (буква Г употреблялась для обозначения звука «п», а не «г»). Дойдя до десяти, они ввели еще один новый символ D, первую букву слова «дека» (десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ H означал 100 (гекатон), X – 1000 (хилиои), символ M – 10000 (мириои или мириада). Используя число 5 как промежуточное подоснование системы счисления, греки на основе принципа умножения комбинировали пятерку с символами степеней числа 10. Так, число 50 они обозначали символом , 500 – символом , 5000 – символом , 50000 – символом . Еще большие числа обычно описывались словами. Число 6789 в аттической системе записывалось в виде .

Вторая принятая в Древней Греции ионическая система счисления – алфавитная – получила широкое распространение в начале Александрийской эпохи, хотя возникнуть она могла несколькими столетиями раньше, по всей видимости, уже у пифагорейцев. Эта более тонкая система счисления была чисто десятичной, и числа в ней обозначались примерно так же, как в древнеегипетской иератической системе. Используя двадцать четыре буквы греческого алфавита и, кроме того, еще три архаических знака, ионическая система сопоставила девять букв первым девяти числам; другие девять букв – первым девяти целым кратным числа десять; и последние девять символов – первым девяти целым кратным числа 100. Для обозначения первых девяти целых кратных числа 1000 греки частично воспользовались древневавилонским принципом позиционности, снова использовав первые девять букв греческого алфавита, снабдив их штрихами слева. Например, число 6789 в ионической системе записывалось как FYPQ. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. Первоначально числа обозначались прописными буквами, но позднее сменились на строчные.

Ионическая система первоначально не сильно потеснила уже установившуюся аттическую или акрофоническую (по начальным буквам слов, означавших числительные) системы исчисления. По-видимому, официально она была принята в Александрии во времена правления Птолемея Филадельфийского и в последующие годы распространилась оттуда по всему греческому миру, включая Аттику. Переход к ионической системе счисления произошел в золотой век древнегреческой математики и, в частности, при жизни двух величайших математиков античности. Есть нечто большее, чем просто совпадение, в том, что именно тогда Архимед и Аполлоний работали над усовершенствованием системы обозначения больших чисел. Архимед, придумавший схему октад (эквивалентную современному использованию показателей степени числа 10), гордо заявлял в своем сочинении «Псаммит» («Исчисление песчинок»), что может численно выразить количество песчинок, необходимых для того, чтобы заполнить всю известную тогда Вселенную. Изобретенная им система обозначения чисел включала число, которое ныне можно было бы записать в виде единицы, за которой следовало бы восемьдесят тысяч миллионов миллионов цифр.

С помощью простого введения диакритических знаков наподобие тех, которые греки применяли для обозначения тысяч, алфавитное обозначение целых чисел можно было бы легко приспособить для обозначения десятичных дробей, но этой возможностью они не воспользовались.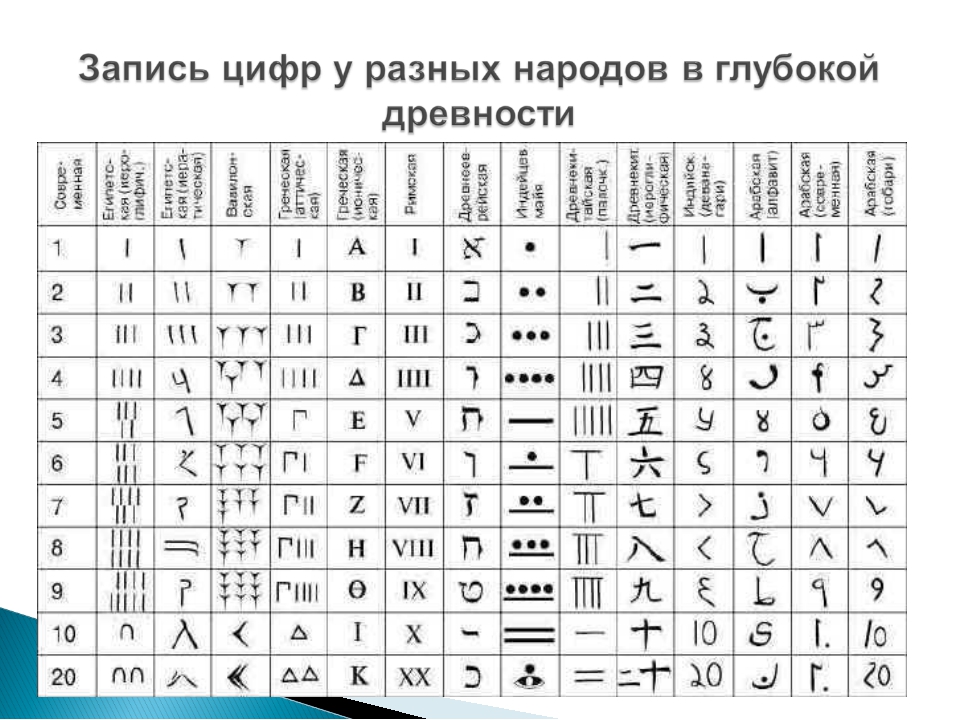 Вместо этого для обозначения дробей греки использовали приемы древних египтян и вавилонян. Египетское влияние в Греции было достаточно сильным, чтобы навязать грекам употребление лишь аликвотных дробей, однако большие вычислительные удобства системы счисления вавилонян побудили живших позднее александрийских астрономов перейти к использованию шестидесятиричных дробей. Переняв систему счисления Древнего Вавилона, греки заменили месопотамскую клинопись своими буквенными обозначениями. Например, Птолемей записал длину хорды, стягивающей дугу в 120° окружности радиусом в 60 единиц, как RGNE?KG?•, т.е. 103 + 55/60 + 23/602 единиц. В более поздний период в вавилонской шестидесятиричной системе имелся специальный символ для обозначения «пустой» позиции, и греческие астрономы ввели для этой цели букву омикрон. Неясно, был ли такой выбор подсказан тем, что с этой буквы начиналось слово оуден (ничто). Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим, чем случайное совпадение, но у нас нет точных данных, позволяющих утверждать это со всей определенностью.

Поскольку греки работали с обыкновенными дробями лишь эпизодически, они использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятиричным дробям.

Недостатки греческих обозначений дробных чисел, включая использование шестидесятиричных дробей в десятичной системе счисления, объяснялись отнюдь не пороками основополагающих принципов. Недостатки греческой системы счисления можно отнести скорее за счет их упорного стремления к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали как набор единиц, поэтому то, что мы теперь рассматриваем как единое рациональное число – дробь, – греки понимали как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике. Кроме того, десятичные представления обыкновенных дробей в большинстве случаев бесконечны. А поскольку бесконечность была исключена из строгих рассуждений, теоретическая арифметика не нуждалась в такого рода представлениях. С другой стороны, областью, в которой практические вычисления испытывали величайшую потребность в точных дробях, была астрономия, а здесь вавилонская традиция была настолько сильна, что шестидесятиричная система обозначений угловых, дуговых и временных величин сохраняется и поныне.

Рим. Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась Римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы. Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Q (или A, или A) и f (или , или ). ). Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Q и f. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX и XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.

В целом римляне не были склонны заниматься математикой, поэтому не испытывали особой потребности в больших числах. Тем не менее для обозначения 10000 они эпизодически использовали символ , а для числа 100000 – символ . Половинки этих символов иногда использовались для обозначения чисел 5000 ( ) и 50000 ( ). Таким образом, в римских обозначениях число 6789 можно было бы записать как .

Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова uncia (унция), обозначавшего одну двенадцатую основной единицы длины.

Обозначения чисел у древних евреев. Семитские народы могут претендовать на роль создателей алфавитного принципа обозначения чисел в том виде, как он использовался в ионической системе. Действительно, с небольшими модификациями этот принцип применялся евреями, сирийцами, арамейцами и арабами. И все же существует мало сомнений в том, что алфавитные обозначения чисел были заимствованы ими у древних греков, по-видимому из Милета, которые изобрели эти обозначения еще в 8 в. до н.э. У евреев использование алфавитных обозначений чисел окончательно вошло в обиход к 2 в. до н.э. Девять букв алфавита использовались для обозначения первых девяти целых чисел; еще девять букв означали первые девять кратных числа 10; остальные буквы использовались для обозначения сотен. Так как букв в алфавите для обозначения всех кратных числа 100 не хватало, в Талмуде числа, превосходящие 400, записывались путем комбинации: например, число 500 обозначалось символами, соответствующими числам 400 и 100, а 900 записывалось как 400 и 400 и 100. Позднее для обозначения чисел, кратных 100 и превосходящих 400, использовались окончательные варианты формы букв или других символов, в результате чего все девять кратных числа 100 получили свои индивидуальные обозначения в виде буквы или специального знака. (См. таблицу обозначений чисел.) Как и в ионической системе счисления, символы для обозначения первых девяти кратных числа 1000 были такими же, как символы, обозначающие первые девять чисел в разряде единиц. Число 6789 евреи записывали как . Так как запись числа 15 в обычном виде как 10 и 5 совпадает с первыми двумя буквами имени Бога Яхве, древние евреи записывали число 15 как 9 и 6. Высказывалось предположение, что по аналогичным причинам древние римляне избегали записывать число IV вместо IIII, т.к. символ IV совпадает с первыми двумя буквами старолатинского написания имени Юпитер.

Америка. Исследователи, путешествовавшие в 16 в. по Центральной Америке, обнаружили цивилизации с высокоразвитыми системами счисления, отличными от тех, которые были известны в Европе. Самыми важными элементами в системе счисления майя были использование позиционного принципа и символа нуля. Если отвлечься от того, что принятая у индейцев майя система счисления была не шестидесятиричной, а двадцатиричной и вместо 10 использовала вспомогательное основание 5, то в остальном принципы были аналогичны тем, которые ранее были в ходу у жителей Древнего Вавилона. В схеме майя точка означала единицу, а повторяющиеся точки – числа до четырех; пятерку обозначала горизонтальная черта, а две и три горизонтальные черты обозначали, соответственно, числа десять и пятнадцать. Для обозначения числа двадцать майя воспользовались позиционным принципом, используя точку, помещенную над символом нуля. (Последний имел вид .)

Числа в системе счисления древних майя записывались в столбец, причем верхние символы были старшими. Самая нижняя позиция соответствовала разряду единиц; «этажом выше» располагалось число двадцаток. Еще выше единица соответствовала не кратным числа 400, как можно было бы ожидать, а кратным числа 360. За исключением этого разряда, связанного, насколько можно судить, с календарными соображениями и продолжительностью года, все остальные более высокие позиции соответствовали степеням числа 20. Число 6789 в системе счисления, принятой у майя, записывалось как

Система счисления у ацтеков в Мексике была более последовательно двадцатиричной, чем у майя, но в остальном менее тонкой, так как не использовала ни позиционный принцип, ни специальный символ для нуля. Точка означала у ацтеков единицу, а для обозначения степеней числа 20 были введены новые знаки: флаг для 20, дерево для 400 и кошелек для 8000. При необходимости другие числа представлялись с помощью повторения этих символов, а от их чрезмерного повторения они избавлялись, вводя специальные промежуточные коллективные знаки: ромбовидный знак для 10 и фрагменты дерева для 100, 200 или 300.

До появления в Северной Америке европейцев индейцы не имели письменности. Исследования древних систем счисления показывают, что используемые названия чисел были в основном прилагательными и лишь в отдельных случаях достигали уровня абстракции, когда они становились существительными. Тем не менее с помощью рисунков или устно индейцы могли выразить число вплоть до миллиона. Системы составления чисел были самыми различными, но примерно половина из них по существу была десятичной.

Китай. Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять. (См. таблицу обозначений чисел.) Первые пять кратных числа 10 обозначались одной, двумя, ?, пятью горизонтальными палочками, а одна, две, три и четыре горизонтальные палочки, к которым сверху приставлялась вертикальная палочка, означали числа 60, 70, 80 и 90. Для обозначения чисел больше 99 использовался позиционный принцип. Число 6789 китайцы записали бы так: . Обозначения чисел с помощью палочек тесно связано со счетом на пальцах и счетной доске, но применялось оно также и в письменных вычислениях.

Во второй китайской системе счисления для обозначения первых девяти целых чисел или символов (см. таблицу обозначений чисел) используют девять различных знаков и одиннадцать дополнительных символов для обозначения первых одиннадцати степеней числа 10. В сочетании с умножением и вычитанием это позволяло записывать любое число меньше триллиона. Если один из символов, обозначающих первые девять целых чисел, стоит перед (при чтении слева направо) символом, означающим степень числа 10, то первое нужно умножить на второе, если же символ одного из девяти первых целых чисел стоит на последнем месте, то это число надлежит прибавить к обозначенному предыдущими символами. В такой системе счисления число 6789 выглядело бы так: , т.е. 6?1000 + 7?100 + 8?10 + 9.

Индия. Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счисления вытеснила аттическую. Вполне возможно, что переход от кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно хоть как-то проследить или восстановить этот переход от древних индийских форм к системе, от которой произошли наши системы счисления. Надписи, найденные в Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками тех, которые получили теперь название индо-арабской системы. Первоначально в этой системе не было ни позиционного принципа, ни символа нуля. Оба эти элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари (см. таблицу обозначений чисел). В индийской системе число 6789 записывалось бы как . Здесь мы впервые встречаемся с элементами современной системы счисления: индийская система была десятичной, цифровой и позиционной. При желании можно даже усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.

Напомним, что позиционная система счисления с нулем возникла не в Индии, поскольку за много веков до этого она использовалась в Древнем Вавилоне в связи с шестидесятиричной системой. Поскольку индийские астрономы использовали шестидесятиричные дроби, вполне возможно, что это навело их на мысль перенести позиционный принцип с шестидесятиричных дробей на целые числа, записанные в десятичной системе. В итоге произошел сдвиг, приведший к современной системе счисления. Не исключена также возможность, что такой переход, по крайней мере отчасти, произошел в Греции, скорее всего в Александрии, и оттуда распространился в Индию. В пользу последнего предположения свидетельствует сходство кружка, обозначающего нуль, с начертанием греческой буквы омикрон. Однако происхождение индийского символа для нуля окутано тайной, так как первое достоверное свидетельство его появления в Индии датируется лишь концом 9 в. Как ни странно, ни греки, ни индийцы не включили в свои системы счисления десятичные дроби, но именно индийцам мы обязаны современной системой записи обыкновенных дробей с числителем, расположенным над знаменателем (но без горизонтальной черты, отделяющей числитель от знаменателя).

Аравия. Современную систему обозначения чисел часто называют арабской, хотя ясно, что она берет начало не из Аравии. До хиджры арабы записывали числа словами, но затем, как это делали ранее греки, они стали обозначать числа буквами своего алфавита. В 772 индийский трактат «Сидданта» был привезен в Багдад и переведен на арабский, после чего стали использоваться две системы записи чисел: (1) в астрономии по-прежнему употребляли алфавитную систему, (2) в торговых расчетах купцы стали применять систему, заимствованную из Индии. Но даже среди тех, кто пользовался индийской системой, начертания цифр, как и в Индии, сильно варьировали. Эти две системы счисления были широко распространены и после распада арабского халифата. В его восточной части пользовались системой, аналогичной той, которая и сейчас встречается в арабском мире. Число 6789 в этой системе записывается как . Однако обозначения чисел в Испании 10 в. настолько сильно отличались по своим начертаниям от приведенных выше, что казались никак с ними не связанными. В испанских обозначениях, получивших название «гобар» или «песчаных», число 6789 выглядело бы так: . Свое название эти обозначения получили потому, что ими пользовались при вычислениях на «песчаном абаке». Как свидетельствует Бируни, индийцы часто производили вычисления на песке, что, возможно, и послужило поводом для такого названия. Тем не менее само происхождение этих цифр, от которых в свою очередь произошли наши современные цифры, остается неизвестным.

Западная Европа. Первым европейским ученым, о котором достоверно известно, что он ввел в употребление в Европе арабские цифры, был Герберт, работавший в Испании и позднее (в 999-м) ставший папой Сильвестром II. В 12 в. Хуан из Севильи перевел на латынь трактат De numero indorum (Об индийских числах) арабского математика Аль-Хорезми. Когда в следующем веке индийские обозначения стали широко известными, новая система получила название алгоритм – от искаженного Аль-Хорезми. Через пару столетий европейские алгоритмики одержали верх и над абацистами, и над теми, кто пользовался римскими цифрами в вычислениях с целыми числами, но лишь с 1585 индо-арабская система обозначений, систематически расширяясь, стала использоваться и применительно к дробям. В том же году Симон Стевин опубликовал свой небольшой трактат De Thiende (Десятина), в котором он предложил записывать в виде или число, которое мы записали бы как 6789. В 17 в. вошла в употребление десятичная запятая (или точка), которой стали отделять целую часть числа от дробной, после чего европейцы отказались от предложенной Стевином индексации разрядов. После этих изменений развитие современной системы счисления завершилось. (Это отнюдь не означает, будто была достигнута полная стандартизация в названиях или обозначениях чисел. В Америке и Франции биллион означает тысячу миллионов, а в Англии и Германии – миллион миллионов; в континентальной Европе часто используется десятичная запятая, а в англосаксонских странах предпочитают ставить десятичную точку; англосаксы используют запятые, чтобы отделять степени тысячи, в некоторых странах для этой цели служит точка.).

 

 

 

Цифры, цифры и цифры

jkWMJVBmYL0

Номер

Число — это счетчик или измерение, которое на самом деле является идеей в нашем сознании.

Мы пишем или говорим о числах, используя цифр , например, «4» или «четыре».

Но мы также можем поднять 4 пальца или 4 раза постучать по земле.

Это разные способы обозначения одного и того же номера.

Существуют также специальные числа (например, π (Пи)), которые нельзя записать точно, но они по-прежнему являются числами, потому что мы знаем, что за ними стоит идея .

Число

Цифра — это символ или имя , обозначающее число.

Примеры: 3 , 49 и двенадцать — все числа.

Итак, число — это идея, цифра — это то, как мы его записываем.

цифра

Цифра — это единичный символ , используемый для составления цифр.

0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — это десять цифр, которые мы используем в повседневных числах.

Пример: цифра 153 состоит из 3 цифр («1», «5» и «3»).

Пример: цифра 46 состоит из 2 цифр («4» и «6»).

Пример: цифра 9 состоит из 1 цифры («9»). Таким образом, одна цифра также может быть цифрой

.

Мы можем использовать и другие символы, например, в шестнадцатеричном формате также используются некоторые буквы!

Цифры -> Цифры -> Цифры

Таким образом, цифры составляют цифры, а цифры соответствуют идее числа.

Также как буквы составляют слова, а слова обозначают идею предмета.

Номер вместо цифры

Но часто люди (в том числе и я) говорят «Число», хотя им действительно следует сказать «Числовое» … неважно, если вы это сделаете, потому что другие люди вас понимают.

Но попробуйте использовать «цифру» только когда говорите об отдельных символах, составляющих цифры, хорошо?

Цифры и цифры других типов

Мы все привыкли использовать такие числа, как «237» и «99», но римляне использовали римские цифры, и на протяжении всей истории использовалось много других цифр и цифр.

10181, 10182, 10183, 10184, 10185, 10186, 10187, 10188, 10189, 10190

основных математических символов | Словарь

математика (BrE) | математика (AmE) — это сокращенная форма математики

На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.

+
плюс / дополнительный знак

Знак плюс означает:

а.понятие

положительное

Любое число больше нуля является положительным числом и может быть написано со знаком плюс перед ним или без него.

Таким образом, +5 (плюс пять) и 5 ​​(пять) — это одно и то же число.

г. операция сложения

3 + 5 = 8
три плюс пять равняется восьми
пять добавленных к трем составляют восемь
три добавленных к пяти дают восемь
если вы добавите пять к трем, вы получите восемь

Сложение дает нам сумму .В 3 + 5 = 8 получается восемь.

—

знак минус / знак вычитания

Знак минус представляет:

а. понятие отрицательного

Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.

-3
минус три

г. операция вычитания

8-5 = 3
восемь минус пять равняется трем
пять вычитаем из восьми равны трем
если вы вычитаете пять из восьми, вы получаете три
, если вы берете пять из восьми, вы получаете три

Вычитание дает нам разницу в . В 8-5 = 3 разница в три.

×

раз знак / знак умножения

Знак раз представляет:

умножение

5 x 6 = 30
пять умножить на шесть равно тридцать
пять умножить на шесть равно тридцать
пять шестерок равно тридцать
если умножить 5 на 6, получится тридцать

Умножение дает нам произведение . В 5 х 6 = 30 получается тридцать.

÷ OR /

разделительный знак

Знак деления означает:

отдел

15 ÷ 3 = 5
15/3 = 5
пятнадцать делить на три равно пять
пять делятся на пятнадцать трижды
если пятнадцать разделить на три, получится пять
если три разделить на пятнадцать, получится пять

Деление

дает нам отношение к .При 15 ÷ 3 = 5 частное равно пяти.

Давайте резюмируем вышеупомянутые четыре операции как:

эксплуатация			счет
дополнение	плюс	2 + 2 = 4	сумма
вычитание	«минус»	5–3 = 2	разница
умножение	«раз»	3 х 5 = 15	товар
отделение	«разделить на»	21/7 = 3	частное

=

знак равенства

Знак равенства представляет равенство :

3 + 4 = 7
три плюс четыре равно семь

Обратите внимание, что мы обычно говорим, что равно НЕ равно:

• два плюс два равно четыре
• два плюс два равны четыре

<
менее

3 <4
три меньше четырех

>

больше

4> 3
четыре больше трех

≠

НЕ равно

x ≠ z
x не равно z

≥

больше или равно

x ≥ z
x больше или равно z

≤

меньше или равно

z ≤ x
z меньше или равно x

¾

дробь

см. Дроби

.

десятичный разделитель | точка

Десятичный разделитель отделяет целое число от дробной части справа:

1,23

В английском языке десятичным разделителем обычно является точка (.). Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,).

см. Десятичные дроби

,

разделитель тысяч

В английском языке разделитель тысяч разделяет целые числа на группы по три справа.

10 987 654 321

В английском языке разделителем тысяч обычно является запятая (,).Обратите внимание, что в некоторых языках разделителем тысяч является точка (.) Или иногда пробел ().

см. Тыс.

%

знак процента

Знак процента указывает число или соотношение в виде доли от 100 ( процентов ).

40%
сорок процентов
За нее проголосовало всего сорок процентов людей.
Какой процент проголосовал за нее? Сорок процентов.

√

корень квадратный

√16 = 4
квадратный корень шестнадцати равен четырем
квадратный корень шестнадцати равен четырем

цифр, символов и знаков препинания на английском языке

Следуйте списку;

Список кардинальных, порядковых и римских цифр;

Порядковые номера

Кардинальные числа		римские цифры
1 — один	1-я — первая	1 — Я
2 — два	2-я — вторая	2 — II
3 — три	3-й — 3-й	3 — III
4 — четыре	4-я — 4-я	4 — IV
5 — пять	5–5	5 — В
6 — шесть	6-6	6 — VI
7-7	7-7	7 — VII
8-8	8-8	8 — VIII
9 — девять	9-9	9 — IX
10 — десять	10–10	10 — Х
11 — одиннадцать	11-11-е	11 — XI
12 — двенадцать	12–12	12 — XII
13 — тринадцать	13–13	13 — XIII
14 — четырнадцать	14–14	14 — XIV
15-15	15-15	15 — XV
16 — шестнадцать	16–16	16 — XVI
17 — семнадцать	17 — семнадцатая	17 — XVII
18–18 лет	18–18	18 — XVIII
19 — девятнадцать	девятнадцатая — девятнадцатая	19 — XIX
20 — двадцать	20-20-е	20 — ХХ
21 — двадцать один	21 — двадцать первая	21 — XXI
30–30 лет	30–30	30 — ХХХ
40 — четверть	40-40	40 — XL
50 — пятьдесят	50-50	50 — L
60 — шестьдесят	60-60	60 — LX
70 — семьдесят	70 — семидесятые	70 — LXX
80 — восемьдесят	80-80	80 — LXXX
90 — девяносто	90 — девяностые	90 — ХС
100 — сто	сотые — сотые	100 — С
500 — пятьсот	500-5 сотых	500 — Д
1000 — одна тысяча	1000-я — одна тысячная	1000 — M

Список символов и знаков препинания;

Обозначение	Значение	Обозначение	Значение
+	плюс	–	минус
x	умножить на	÷	делить на
=	равно	>	больше
<	менее	%	процентов
и	и	@	при
°	градусов	√	квадратный корень
π	пи	$	доллар
©	авторское право	.	полная остановка
,	запятая	;	точка с запятой
:	толстая кишка	?	вопросительный знак
!	восклицательный знак	–	тире
*	звездочка	()	скобки
«»	кавычки	‘	апостроф

Синхронность, символизм и значение чисел ⋆ LonerWolf

Числа древние, значимые и могущественные.

Именно пифагорейцы в VI веке до нашей эры были одной из первых групп, популяризировавших идею о том, что числа — это не просто математические символы, но на самом деле они имеют духовное значение . Как однажды цитировали Пифагора, «Число — властитель форм и идей и причина богов и демонов».

Благодаря Пифагору у нас появилась нумерологическая система, которая приписывает числам разные значения. Но нумерология — это только одна сторона медали: числам придавалось особое значение на протяжении всей истории, религии и культурной мифологии.От Дальнего Востока до нашего собственного западного наследия числа несли значение на протяжении тысячелетий.

Числа и синхронность

Сколько раз вы видели повторяющиеся числа, такие как 11:11, 777, 1010, 4444, 999 и т. Д.?

Наблюдение за повторяющимися числами — это форма синхронности — феномен, описанный психиатром Карлом Юнгом как «значимое совпадение двух или более событий, в котором присутствует нечто иное, чем вероятность случайности».”

Другими словами, синхронность — это гораздо больше, чем интуитивная интуиция, предполагающая удачу и случайность. Синхронистичность рождается из области бессознательного и эфирного царства. Когда мы переживаем синхронность, нам посылают знаки и сообщения из нашего бессознательного разума и Высшего Я.

Например, Юнг описал ситуацию синхронности, когда он обратил внимание на символ получеловека, наполовину рыбы. Затем ему подали рыбу на обед. Кто-то пошутил о том, чтобы сделать из другого «апрельскую рыбку».Днем один из его пациентов показал ему фотографию рыбы. Вечером другой человек показал ему вышивку с морскими чудовищами и рыбками. На следующее утро его следующая пациентка поделилась с ним сном о рыбе.

Синхронность на самом деле может сильно нервировать, особенно когда определенные символы — и в данном случае числа — продолжают появляться.

Если вы видите одно и то же число снова и снова, важно, чтобы вы попытались изучить символику, которую это число содержит для вас.Повторяющиеся числа, символы и слова, которые вы постоянно слышите, имеют огромное значение в вашей жизни, и вам следует уделять им пристальное внимание.

Числа и символика

На протяжении всей истории числа стали означать разные вещи для разных культур. Однако в целом числа получили аналогичные значения.

Возьмем, к примеру, число четыре. Коренные американцы верят, что существует четыре ветра и четыре направления. Аналогичным образом древние греки считали, что существует четыре элемента.В христианстве четыре — это число творения (то есть в четвертый день недели Бог завершил создание материальной вселенной). Как мы видим, четыре имеет очень похожее значение в трех совершенно разных периодах времени и культурах.

Только примечание. Я хочу подчеркнуть, что, хотя выяснять общее значение чисел полезно, совершенно необходимо, чтобы вы узнали свое личное значение . Синхронность, символизм и значение чисел — все это очень личное.

Может возникнуть соблазн не прилагать никаких усилий и просто придерживаться традиционного значения числа. Пожалуйста, не делай этого. Гораздо лучше немного поработать и изучить, что значение чисел означает в первую очередь для ВАС.

Вот несколько способов узнать, что каждое число означает для вас и вашего контекста:

• Запишите каждое слово, связанное с этим числом. Например, если вы продолжаете видеть число 2, вы можете написать: «мужчина и женщина, отношения, инь и янь, двойственность, свет и тьма, верх и низ, материальное и духовное…»
• Что приходит вам на ум? После того, как вы увидите серию повторяющихся чисел, у вас может сразу возникнуть мысль или предположение о том, что это число означает.Не игнорируйте эту немедленную интерпретацию! Запишите это или запишите. Часто значения, которые мы сначала приписываем числам, которые мы видим, наиболее верны, потому что для этого требуется небольшое умственное усилие. Чем больше умственных усилий, тем больше мы начинаем выдумывать значения.
• Какое толкование вызывает у вас сильные чувства? Многие люди спрашивают меня, как узнать, верна ли их интерпретация числа. Мой ответ — обратить внимание на то, как запускается интерпретация. Например, вызывает ли ваш анализ чувство возбуждения, трепета, страха, ликования или даже просто вызывает покалывание по позвоночнику? Это хороший признак того, что вы нашли правильное объяснение, потому что ваше тело реагирует очень сильно. Однако, если интерпретация кажется вам холодной, плоской или отстраненной, вероятно, она не подходит.

Значение чисел

Ниже я поделюсь с вами общим мнением мифологии, религии, мистицизма и эзотерики относительно каждого числа. Как я уже упоминал, важно, чтобы вы нашли свое собственное значение, но это действительно помогает узнать, что означает каждое число. Иногда мы действительно настраиваемся на традиционную энергию, магию и значение каждого числа:

Номер 0

Ноль представляет собой изначальную пустоту, матку, царство потенциала.Ноль — это круг, который символизирует тотальность: то, что предшествует жизни, вечной силе. Это ничто и все, начало и конец. Ноль часто является символом Духа или Бога и, следовательно, единства и целостности.

Номер 1

Один символизирует лидерство, силу и уверенность. Номер один похож на прямую стрелу, которая отражает силу воли и точность. Один также отражает индивидуальность, самопознание и расширение возможностей. В отличие от ноля, который женственен и восприимчив, у человека есть мужская и волевая энергия.

Номер 2

Два — это число двойственности; раскол, который мы воспринимаем в жизни, между светом и тьмой, внутренним и внешним, инь и янь, мужским и женским, добром и злом, жизнью и смертью, разумом и сердцем и так далее. С одной стороны, двое символизируют партнерство, а с другой — конфликт и противостояние. В сбалансированном состоянии два — это число гармонии, но в несбалансированном состоянии число два может быть разрушительным.

Номер 3

Три обычно считается особенно удачным и сильным числом.Три представляет собой божественный принцип, лежащий в основе жизни, такой как разум, тело и дух; рождение, жизнь и смерть; начало, середина и конец; прошлое, настоящее и будущее и так далее. Духовные традиции, такие как Викка и христианство, символизируют духовную силу как триединую, например, Отец, Сын и Святой Дух, а также Деву, Мать и Старуху. Три символизируют успех, интуицию и удачу.

Номер 4

Четыре — это обоснованное и стабильное число, вызывающее чувство спокойствия и солидности.Четверка во многом укоренена в физическом мире и означает присутствие и «сейчас». Например, есть четыре сезона, четыре элемента и четыре угла земли. Четыре — это создание прочного фундамента и развитие приземленной перспективы.

Номер 5

Пятерка — это число приключений и свободы. Пять — это тоже очень чувственное число (пять чувств, пять пальцев рук и ног), и оно говорит о том, чтобы наслаждаться жизнью, пробовать новые впечатления и искать удовольствия.Это число также связано с переменами в жизни (например, замужеством, разводом, новой работой) и принятием важных решений.

Номер 6

Шесть представляет собой баланс между земным и духовным царствами. Шесть также связаны с интуицией, ясновидением и другими экстрасенсорными способностями (отсюда «шестое» чувство). В нумерологии шесть — это число смотрителя; человек, который заботится о других и милосердно служит им.

Номер 7

Семь — магическое число, связанное с синхронностью, удачей и совершенством (семь чакр, семь цветов радуги, семь дней в неделе и т. Д.). Семь также рассматривается как мистическое число, связанное с духовным пробуждением, самоанализом и развитием мудрости. Это число связано со стремлением к Истине и стремлением к более глубокому пониманию жизни.

Номер 8

Восьмерка связана с изобилием, процветанием и финансовым благополучием. Находчивость, трудолюбие, решительность и внутренняя сила — качества восьми. В духовном плане восьмерка рассматривается как уравнитель или балансир (отсюда и его форма), который объединяет сознательное с бессознательным, а земное — с духовным.Другими словами, восьмерка отражена в пословице: «Что посеешь, то и пожнешь».

Номер 9

Девять — это число исполнения. Мудрость, самоанализ, просветление и высшее сознание — все это качества, связанные с числом девять. Девять также связаны с высшей целью и высшей жизненной миссией; это число побуждает нас взглянуть на нашу жизнь с высоты птичьего полета.

Номер 10

Десять представляет завершение: окончание цикла и достижение целостности.Десять — это одновременно мужское и женское начало, и оно отражает единство, которое становится возможным, если мы объединяем фрагментированные части нашего внутреннего «я».

---

Электронная книга «Процесс духовного пробуждения»:

Откройте для себя глубокие идеи и практики, которые помогут вам достичь глубоких уровней любви и свободы. Исследуйте возвращение души, работу с тенью и многое другое. Начните свое путешествие по духовному пробуждению прямо сейчас!

---

Номер 11

Одиннадцать — мощное число, которое часто называют «духовным посланником».«Это число несет в себе как положительные, так и отрицательные ассоциации. С одной стороны, одиннадцать может означать необходимость срочных изменений (отсюда и поговорка «одиннадцатый час»), но с другой стороны, одиннадцать связаны с судьбой. Другими словами, одиннадцать человек могут многое рассказать о вашем жизненном пути и о том, какими путями вы должны или не должны идти. Луна более подробно рассказала о номере одиннадцать в этой статье 11 11.

Номер 12

Двенадцать — это число космического порядка.Например, в году двенадцать месяцев, двенадцать астрологических знаков, двенадцать часов в день, двенадцать архетипов личности и т. Д. Согласно нумерологии, двенадцать — это число творческого и индивидуального самовыражения.

***

Понимание значения чисел дает вам дополнительный уровень понимания, когда дело доходит до самопознания и реализации. Хотя личное значение, которое вы приписываете числам, может не всегда соответствовать приведенным выше описаниям, я надеюсь, что эти объяснения помогут пролить некоторое понимание.

Лично я заметил повторяющиеся числа и исследовал их значение, что помогло мне кристаллизовать многих важных идей. Многие из этих открытий помогли изменить ход моей жизни. Так что обращать внимание на значение чисел и синхронность — непростая задача! Иногда вы будете видеть повторяющееся число, например 1010 или 555, которое помогает подтвердить решение, которое вы давно хотели принять. Обратите внимание, ведь ваша Душа и Вселенная часто посылают вам такие знаки.

математических символов — список символов, решенные примеры

Math — это все о числах, символах и формулах. Математические символы используются для разных целей в разных математических областях. Использование символов для представления математической информации упрощает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте посмотрим на общие, которые мы используем в разных областях математики.

Если мы напишем слова «прибавление 4 к 2 дает 6» несколько раз, это может усложнить ситуацию.Эти слова также занимают больше места и требуют времени для написания. Вместо этого мы можем сэкономить время и место, используя символы. Язык и словарь математики содержат большое количество символов, и этот список бесконечен — некоторые из них более технические, чем другие. У нас есть как минимум 10 000+ символов, и некоторые из них мы используем редко. Наиболее распространенные символы перечислены в следующей таблице:

Символы	Значение	Примеры математических символов
+	Добавить	5 + 4 = 9
–	Вычесть	5–4 = 1
=	равно	1 + 1 = 2
\ (\ эквив \)	Идентично	(a + b) 2 \ (\ Equiv \) a 2 + 2ab + b 2
\ (\ приблизительно \)	Примерно	\ (\ пи \ около 3.14 \)
\ (\ neq \)	Не равно	5 + 4 \ (\ neq \) 1
\ (\ раз \)	Умножить	5 \ (\ раз \) 4 = 20
\ (\ div \)	Разделить	10 \ (\ div \) 2 = 5
\ (<\)	Менее	10 \ (<\) 20
\ (> \)	Больше	20 \ (> \) 10
\ (\ leq \)	Меньше или равно	х + у \ (\ leq \) z
\ (\ geq \)	Больше или равно	х + у \ (\ geq \) г
\ (\% \)	В процентах	50% = \ (\ begin {align} \ frac {50} {100} \ end {align} \)
\ (.\)	Десятичная точка или период	\ (\ begin {align} \ frac {1} {2} = 0,5 \ end {align} \)
\ (- \)	Винкулум Она разделяет числитель и знаменатель	\ (\ begin {align} \ frac {2} {3} \ end {align} \)
\ (\ sqrt {} \)	Квадратный корень	\ (\ sqrt {4} = 2 \)
\ (\ sqrt [3] {x} \)	Кубический корень x	\ (\ sqrt [3] {27} = 3 \)
\ (\ sqrt [n] {x} \)	n th корень \ (x \)	\ (\ sqrt [4] {16} = 2 \)
\ (() \)	Круглые скобки	\ (2+ (5-3) = 2 +2 = 4 \)
\ ([\: \:] \)	Квадратные скобки	\ (\ begin {align} & 3 \ times [2 + (5 -2)] +1 \\ & 3 \ times [2 + 3] +1 \\ & 3 \ times5 + 1 \ & 16 \ end {align} \)
\ (\ {\} \)	Держатель для цветов	\ (\ begin {align} & 16 \ div \ {3 \ times [2 + (5 -2)] +1 \} \\ & 16 \ div \ {3 \ times [2 + 3] +1 \} \\ & 16 \ div \ {3 \ times5 + 1 \} \\ & 16 \ div \ {16 \} \\ & 1 \ end {align} \)
\ (\ дюйм \)	Принадлежит к	0 \ (\ in \) Целое число
\ (\ not \ in \)	Не относится к	\ (\ frac {1} {2} \ not \ in \) Натуральные числа
\ (\ следовательно \)	Следовательно	\ (x + 1 = 2 \, следовательно, x = 1 \)
\ (\ потому что \)	Потому что	\ (\ begin {align} \ frac {1} {2} \! \ Div \! 0.5 \! = \! 1 (\ потому что \! \ Frac {1} {2} \! = \! 0.5) \ end {align} \)
\ (\ infty \)	бесконечность	Бесконечность бесчисленна, \ (\ begin {align} \ frac {1} {3} \ end {align} \) при записи в десятичной форме, бесконечен \ (0,333 ….. \)
\ (! \)	Факториал	\ (5! \ \! \! = \! 5 \! \ Раз \! 4 \! \ Раз \! 3 \! \ Раз \! 2 \! \ Раз \! 1 \)

Константы, используемые как математические символы

Мы используем константы в математике для обозначения неизменяющихся объектов.Эти константы могут включать ключевые математические наборы, ключевые числа, ключевые математические бесконечности и другие ключевые математические объекты (такие как единичная матрица). Эти математические константы чаще всего имеют форму буквы алфавита или производной от нее. В следующей таблице перечислены некоторые из наиболее часто используемых констант, а также их имя, значение и использование.

Символ Название	Пояснение
0 (ноль)	Аддитивное тождество общих чисел
1 (один)	Мультипликативное тождество общих чисел
√2 (квадратный корень из 2)	Положительное число, квадрат которого равен 2.Примерно равно 1,41421.
e (постоянная Эйлера)	Основание натурального логарифма. Предел последовательности (1 + (1 / n) n ). Примерно равно 2,71828
\ (\ pi \) (Пи, постоянная Архимеда)	Отношение длины окружности к ее диаметру. Половина окружности единичной окружности. Примерно равно 3,14159
\ (\ phi \) (Фи, золотое сечение)	Соотношение между большим числом и p меньшим числом q, когда (p + q) / p = p / q.Положительное решение уравнения y 2 -y-1 = 0.
i (Мнимая единица)	Главный корень -1. Основополагающий компонент комплексного числа.

Математические символы, используемые в логике

В следующей таблице показаны математические символы, используемые в логике.

Символы	Значение	Примеры математических символов
\ (\ существует \)	Существует как минимум один	∃ x: P (x) ∃ x: F (x) Существует хотя бы один элемент из p (x), \ (x \), такой, что F (x) истинно.2> 1 \)
\ (\ neg \)	Логическое НЕ	Утверждение A истинно, только если \ (\ neg \) ложно \ (х \ neq y \ iff \ neg (x = y) \)
\ (\ lor \)	Логическое ИЛИ	Утверждение A \ (\ lor \) B верно , если A или B истинно; , если оба ложны, заявление ложное.
\ (\ земля \)	логический и	Утверждение A \ (\ land \) B верно , если оба A и B истинны; иначе это ложь.
\ (\ подразумевает \)	Подразумевает	х = 2 \ (\ подразумевает \) x 2 = 4
\ (\ iff \)	Если и только если	х +1 знак равно у +1 \ (\ iff \) х = у
\ (\ text {|} \) или \ (\ text {:} \)	Такое, что	{\ (x \) | \ (x \)> 0} = {1,2,3, …}

Диаграмма Венна и символы теории множеств

В следующей таблице показаны математические символы, используемые в диаграммах Венна и теории множеств.

.

Символы	Значение	Примеры математических символов
\ (\ cap \)	Перекресток	A = {2,3,4} B = {4,5,6} A \ (\ cap \) B = {4}
\ (\ чашка \)	Союз	A = {2,3,4} B = {4,5,6} A \ (\ cup \) B = {2,3,4,5,6}
\ (\ varnothing \)	Пустой набор	Комплект без элементов \ (\ varnothing \) = {}
\ (\ дюйм \)	является участником	2 \ (\ in \) \ (\ mathbb {N} \)
\ (\ notin \)	не является участником	0 \ (\ notin \) \ (\ mathbb {N} \)
\ (\ подмножество \)	Подмножество	\ (\ mathbb {N} \ subset \ mathbb {I} \)
\ (\ supset \)	— это надмножество	\ (\ mathbb {R} \ supset \ mathbb {W} \)
\ (\ text {P (A)} \)	Силовой агрегат А	P ({1,2}) = {{}, {1}, {2}, {1,2}}
\ (А = В \)	Равенство (те же элементы в наборе A и наборе B)	A = {1,2}; B = {1,2} \ (\ подразумевает \) A = B
\ (А \ раз В \)	Декартово произведение Комплект заказанных пар от А и Б	A = {5,6}; B = {7,8} \ (\ подразумевает \) \ (A \ times B \) = {(5,7), (5,8), (6,7), (6,8)}
\ (\ text {| A |} \)	Мощность — это количество элементов в наборе A	| {1,2,3,4} | = 4

Цифровые символы

Цифровые символы с их примерами и соответствующими индо-арабскими цифрами перечислены здесь в таблице.

Символы	Значение	Примеры математических символов
Римская цифра I	значение = 1	I = 1, II = 2, III = 3
Римская цифра V	значение = 5	IV = 4 (5-1) VI = 6 (5 + 1) VII = 7 (5 + 2) VIII = 8 (5 + 3)
Римская цифра X	значение = 10	IX = 9 (10-1) XI = 11 (10 + 1) XII = 12 (10 + 2) XIII = 13 (10 + 3)
Римская цифра L	Значение = 50	XLIX = 49 (50-1) LI = 51 (50 + 1) LIX = 59 (50 + 9) LXI = 61 (50 + 11)
Римская цифра C	Значение = 100 (Век)	CC = 200 (100 + 100) CCLIX = 259 (100 + 100 + 50 + 9)
Римская цифра D	Значение = 500	DCLI = 651 (500 + 100 + 50 + 1) DCCIV = 704 (500 + 100 + 100 + 4)
Римская цифра M	значение = 1000	ММ = 2000 (1000 + 1000) MMCCLV = 2255 (1000 + 1000 + 100 + 100 + 50 + 5)
R или \ (\ mathbb {R} \)	Реальные числа	\ (\ frac {1} {2}, \ frac {1} {4}, 0.5 \) \ (\ sqrt {2}, \ sqrt {3} \)
Z или \ (\ mathbb {Z} \)	Целое число	-100, -20,5,10, ….
N или \ (\ mathbb {N} \)	Натуральные числа	1,2,3, … 500, …
Q или \ (\ mathbb {Q} \)	Рациональные числа	\ (- \ frac {1} {2}, \ frac {1} {4}, 0,5 \)
P или \ (\ mathbb {P} \)	Иррациональные числа	\ (\ sqrt {2}, \ sqrt {3} \)
C или \ (\ mathbb {C} \)	Комплексные числа	5 + 2i

Символы геометрии и алгебры

В приведенной ниже таблице показаны наиболее часто используемые геометрические символы.Математические символы с названиями и примерами также перечислены в таблице.

Символы	Значение	Примеры математических символов
\ (\ угол \)	Упомяните угол	\ (\ угол ABC \)
\ (\ Дельта \)	Треугольник	\ (\ Delta \ text {PQR} \)
\ (\ конг \)	Соответствует	\ (\ Delta \ text {PQR} \ cong \ Delta \ text {ABC} \)
\ (\ sim \)	Похож на	\ (\ Delta \ text {PQR} \ sim \ Delta \ text {ABC} \)
\ (\ перп \)	Перпендикулярно	AB \ (\ perp \) PQ
\ (\ параллельно \)	Параллельно	AB \ (\ параллельно \) CD
\ (^ \ circ \)	степень	\ (60 ^ \ circ \)
\ (\ overline {\ rm AB} \)	Отрезок AB	Линия A от точки A до точки B
\ (\ overrightarrow {\ rm AB} \)	Ray AB	Линия, начинающаяся из точки A и продолжающаяся через точку B
\ (\ overleftrightarrow {\ rm AB} \)	Линия AB	Бесконечная прямая, проходящая через точки A и B
\ (\ нахмуриться \ поверх AB \)	Дуга от A до B	\ (\ frown \ на вершине AB = 60 ^ \ circ \)
\ (^ c \)	символ радианов	\ (360 ^ \ circ = 2 \ pi \: ^ c \)

Алгебраные символы

В следующей таблице показаны наиболее часто используемые алгебраические символы.Математические символы с названиями и примерами также перечислены в таблице.

Символы	Значение	Примеры математических символов
\ (х, у \)	Переменные	\ (х = 5 \), \ (у = 2 \)
\ (+ \)	Добавить	\ (2х + 3х = 5х \)
\ (- \)	Вычесть	\ (3х-х = 2х \)
\ (. \)	Товар	\ (2x.2 \)
\ (\ neq \)	Не равно	\ (a + 5 = b + 1 \ влечет a \ neq b \)
\ (= \)	равно	\ (а = 5 \)
\ (\ propto \)	Пропорционально	\ (x \ propto y \ подразумевает x = ky \)
\ (f (x) \)	Функция отображает значения \ (\) x в \ (f (x) \)	\ (е (х) = х +3 \)

Греческие алфавиты и символы комбинаторики

В таблице ниже показаны греческие алфавиты, которые используются в качестве математических символов.Их названия, использование и примеры также перечислены в таблице.

Символы	Значение	Примеры математических символов
\ (\ alpha \)	Альфа	Используется для обозначения углов, коэффициентов
\ (\ beta \)	Бета	Используется для обозначения углов, коэффициентов
\ (\ гамма \)	Гамма	Используется для обозначения углов, коэффициентов
\ (\ Дельта \)	Дельта	Дискриминантный символ
\ (\ varepsilon \)	Эпсилон	Используется для обозначения универсального набора
\ (\ iota \)	Йота	представляет собой мнимое число
\ (\ лямбда \)	Лямбда	Представляет константу
\ (\ pi \)	Pi	\ (\ пи \ около 3.14 \)
\ (\ Sigma \)	Sigma	Представляет собой сумму
\ (\ тета \)	Тета	Обозначает углы
\ (\ rho \)	Rho	Статистическая константа
\ (\ phi \)	Phi	Обозначение диаметра

Комбинаторические символы

В таблице ниже показаны обычно используемые символы комбинаторики.6 {P_4} & = 6 \ times 5 \ times 4 \ times 3 = 360 \ end {align}

Статьи по теме о математических символах

Просмотрите следующие страницы, посвященные математическим символам.

Важные примечания

Вот список из нескольких моментов, которые следует помнить при изучении математических символов:

• Использование символов для представления информации упрощает понимание математических выражений.
• У нас как минимум 10 000 символов, и некоторые из них мы используем редко.
• Мы используем константы в математике для обозначения неизменяющихся объектов.

Что такое U в математических символах?

Математический символ U используется для обозначения набора, полученного путем объединения элементов двух наборов. Следовательно, объединение двух наборов P и Q будет набором элементов в P и Q. Для обозначения набора используется специальный символ ∪, который выглядит как «U».

Сколько существует математических символов?

Имеется более 10000 математических символов. Некоторые из основных: =, +, -, ≠, ±, * и так далее.Есть сложные символы, такие как \ (\ alpha \), \ (\ varepsilon \) и так далее.

Какой математический символ используется для периода волны?

Математический символ, который используется для обозначения периода волны, — λ. Это также известно как длина волны, которая измеряется в единицах расстояния.

Каково использование математического символа сложения?

Символ сложения (+) обычно используется при добавлении двух или более чисел, например, 5 + 5. Помимо этого, символ (+) также может использоваться для обозначения положительного числа, например +7.

Список некоторых общих арифметических математических символов.

Некоторые из общих арифметических математических символов: знак плюс (+), используемый для сложения, знак минуса (-), используемый для вычитания, знак звездочки (*) или знак времени (×), используемый для умножения, и знак деления (÷) или знак косой черты (/) используется для разделения.

От цифр к информации о величине

значений чисел состоит из ассоциации между

числовой информацией и кодами двигателя, относящимися к величине —

предположение, которое соответствует идее, что величина представляет

представлений для чисел и действий имеют общие когнитивные коды

в рамках общей системы размеров и количества (Walsh

2003).

Поскольку понятие воплощенного познания является одной из самых спорных

спорных гипотез недавних психолингвистических

двухкодовых моделей концептуальной обработки, принцип моторного резонанса

также следует рассматривать в контексте обработки чисел

. модели. В заключение мы полагаем, что идея

о семантике чисел, основанных на действии, может дать новое понимание природы представлений числовой величины,

,

и тем самым может внести плодотворный вклад в будущие теоретические разработки

в исследованиях математического познания.

Инактивация и адаптация числа

нейронов

doi: 10.1017 / S0140525X099

Дж. Патрик Мэйо

Отделение нейробиологии, Центр нейронных основ познания, Центр

gh, Университет Пиронауки Pittsburgh,

Pittsburgh, PA 15260.

[email protected]

Резюме: Запись одного нейрона может помочь решить проблему представления абстрактных чисел

в теменных долях.Две манипуляции, в частности, в

— обратимая инактивация и адаптация кажущейся численности

— могут дать важную информацию о причинном влиянии

активности «нумеронов». Взятые вместе, эти тесты могут значительно продвинуть наше понимание обработки чисел в мозге.

Коэн Кадош и Уолш (CK&W) представили исчерпывающий аргумент против абстрактного представления чисел в плоских долях par-

.Их обсуждение сосредоточено на поведенческих исследованиях и исследованиях нейровизуализации

, которые составляют основную часть многочисленной литературы. Но, как указывает CK&W, эти методы

не обеспечивают разрешение выборки, необходимое для окончательного ответа

на вопрос об абстрактном представлении чисел. Напротив, электрофизиология одиночных нейронов

обеспечивает высокое пространственное и временное разрешение

, позволяя исследователям отслеживать активность

отдельных нейронов в реальном времени.Таким образом, этот метод

является наиболее многообещающим средством решения проблемы представления абстрактных чисел

. В этом комментарии я представляю две экспериментальные манипуляции с одним нейроном

, которые, насколько мне известно, не использовались в исследованиях чувствительных к числам нейронов

. Эти манипуляции могут помочь продвинуть исследования одиночных клеток

за пределы простой корреляции к более каузальному пониманию нейронной основы обработки чисел.

Во-первых, временная фармацевтическая инактивация (Li et al. 1999;

Wardak et al. 2002) числовых участков теменной коры

может быть использована для проверки полезности представленных числовых представлений

. Хотя было бы сложно продемонстрировать

, что все нейроны в теменной доле были инактивированы, большая часть

нейронов может быть надежно «выключена» и повторно активирована с течением времени. Соответственно, животные должны демонстрировать серьезное снижение производительности при выполнении задач, связанных с числами, во время инактивации

, если нумероны действительно поддерживают их способность точно обрабатывать числовые значения

.Следуя задачам, рассмотренным в

целевой статье, производительность задач, связанных с числами, должна быть оценена в

в различных числовых форматах. Наличие

представлений абстрактных чисел предсказывает сравнимое

снижение производительности независимо от числового формата при

по сравнению с измерениями до инактивации. Таким образом, временное отключение

— это один из способов, с помощью которого наше понимание представлений чисел

может выйти за рамки корреляционных свидетельств

.

Если абстрактные числовые нейроны существуют, то, предположительно,

лежат в основе нашей способности воспринимать и обрабатывать различные числа.

Таким образом, чтобы выявить влияние числовых нейронов на восприятие, было бы полезно иметь ситуацию, в которой воспринимаемой численностью

можно управлять независимо от отображаемой численности

. К счастью, такой психофизический «трюк» был недавно обнаружен

(Burr & Ross 2008; см. Также Durgin

2008).

Вторая манипуляция включает парадигму «кажущейся численности

адаптации» (Burr & Ross 2008). В этом задании испытуемые

фиксируют центральную цель, в то время как представлены две области, состоящие из множества стационарных стимулов

, одна слева и одна — справа от фиксации

. Сразу после продолжительного периода адаптации тестовые участки затем представляются в тех же двух местах

, и испытуемых просят вынести численное суждение, обычно в

в форме двухальтернативного задания с принудительным выбором (e .g., «Какой патч

содержит больше элементов, слева или справа?»). Берр и Росс

(2008) показали, что адаптация к большому количеству стимулов

снижает последующие суждения о численности, в то время как адаптация к

небольшому количеству стимулов порождает искусственно увеличенные суждения о численности

. Таким образом, числовое восприятие субъектов может управляться управляемым образом на основе

стимулов в адаптирующейся области.

Для записи одиночных нейронов эта задача может быть пассивно передана животным субъектам. Еще лучше, животных можно обучить тому, чтобы

выносили суждения «больше» или «меньше», когда два тестовых участка

представлены после адаптации. Затем мы можем спросить, как число

нейронов в теменной коре отвечает с течением времени в задаче адаптации

(то есть во время и после адаптации). Например, если нейрон

с предпочтительной численностью 20 (Nieder & Merten

2007) изолирован и животное адаптировано с участком из 100 стимулов

, последующее тестовое предъявление 20 стимулов

вызовет нейрон максимально активен в соответствии с достоверным представленным числом

? Или, альтернативно, ответ нейрона

сместится в сторону адаптированной численности в соответствии с восприятием субъекта

? Опять же, различные форматы числовых стимулов также могут быть использованы для адаптации и тестирования (Diester & Nieder, в печати).В соответствии с гипотезой кодирования маркированных строк (Nieder & Merten

2007), избирательность числовых элементов должна предсказуемо изменяться

путем адаптации с низкой и высокой численностью в разных форматах. Серия

условий систематической адаптации и тестирования одного и того же нейрона

поможет выяснить функциональную роль нейронов

и пролить свет на проблемы автоматизма и интенциональности, поднятые CK&W.

Комбинация двух манипуляций может оказаться наиболее плодотворной для

.Изменения в производительности задачи во время инактивации —

как в стандартной задаче отложенного сопоставления с образцом (обычно

, используемой Нидером и его коллегами), так и в задаче адаптации, предложенной выше

, — можно использовать для оценки функции числовых нейронов. в судебных решениях

о численности. Это исследование может быть расширено до

предполагаемых численно-чувствительных нейронов в префронтальной коре (ПФК).

Это расширение поможет устранить неоднозначность роли теменных нейронов и

префронтальных числовых нейронов, а также позволит проверить гипотезу

CK&W о том, что PFC играет «пост-репрезентативную» роль

в отношении обработки чисел в теменной доли.

Эти две манипуляции, конечно же, не полные эксперименты. Но они основаны на устоявшихся методах в области

, которые находятся в пределах наших текущих возможностей. Бремя проведения

этих экспериментов лежит на сторонниках представления абстрактных чисел

, потому что, как подчеркивает CK&W, в настоящее время существует слишком много проблем интерпретации

, чтобы сделать вывод в пользу абстрактности.

Независимо от того, для обеих сторон проблемы, простая манипуляция с ответами отдельных нейронов кажется наиболее определяющим методом для раскрытия абстрактности репрезентаций чисел в теменных долях.

БЛАГОДАРНОСТИ

Это исследование было поддержано фондом Альфреда П. Слоана и Национальным институтом здравоохранения

R01-EY017592 доктору Марку А. Соммеру и стипендиатом Меллона из

Университета Питтсбурга Дж. Патрику Мэйо.

Комментарий / Коэн Кадош и Уолш: Числовое представление в теменных долях

342 НАУКИ О ПОВЕДЕНИИ И МОЗГЕ (2009) 32: 3/4

Как сравнивать числа с математическими символами — Видео и стенограмма урока

Больше

Первый символ, который мы обсудим, — это символ больше .Этот символ выглядит так:>. Большее число идет с левой стороны. Если вы посмотрите на символ, вы увидите, что одна сторона больше, чем другая. Если большая сторона обращена влево, значит, вы смотрите на символ «больше». Чтобы использовать его для сравнения двух чисел, мы пишем наше большее число слева, например: 10> 8.

Меньше

Нашим следующим символом является символ меньше . Этот символ выглядит так: <. Меньшее число идет с левой стороны.Посмотрев на этот символ, вы увидите, что теперь большая сторона обращена вправо, а меньшая сторона обращена влево. Чтобы использовать этот символ, мы пишем меньшее число слева, например: 8 <10.

Equal To

Третий и последний символ, который мы обсуждаем в этом уроке, — это , равный . Этот символ сообщает вам, когда два числа равны друг другу. Выглядит это так: =. Вы будете использовать этот символ, когда числа на обеих сторонах одинаковы, например: 10 = 10.

Примеры

Я использовал всего пару чисел, чтобы показать вам, как работают символы. Эти символы можно использовать с любыми двумя числами, и вы встретите их в тестах по математике. У вас может возникнуть проблема с просьбой записать правильный символ, чтобы показать взаимосвязь между двумя числами. Например, вы можете столкнуться с такой проблемой, когда вас попросят ввести правильный символ в поле между двумя числами:

Вы смотрите на два числа и должны решить, больше ли число слева, меньше или равно числу справа.Глядя на эти два числа, вы видите, что число слева меньше числа справа, поэтому правильным символом для вставки в поле является символ меньше <.

Что с этой проблемой?

Какой символ помещен в эту рамку?

Глядя на свои числа, вы видите, что число слева, 76, больше, чем число справа, 67. Итак, правильный символ, который стоит в рамке, — это символ больше>.

Итоги урока

Давайте рассмотрим то, что мы узнали.