| Символ (TeX) | Символ (Unicode) | Назва | Значення | Приклад |
|---|---|---|---|---|
| Вимова | ||||
| Розділ математики | ||||
| ⇒{\displaystyle \Rightarrow \,} | ⇒ | Імплікація, слідування | A⇒B{\displaystyle A\Rightarrow B\,} означає «коли A{\displaystyle A} істинне, то B{\displaystyle B} також істинне». Іноді використовують →{\displaystyle \rightarrow \,}. | x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4\,} істинне, але x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2\,} хибно (тому що x=−2{\displaystyle x=-2} також є розв’язком). |
| «з… випливає» або «якщо…, то…» | ||||
| скрізь | ||||
| ⇔{\displaystyle \Leftrightarrow } | ⇔, ↔ | Рівносильність | A⇔B{\displaystyle A\Leftrightarrow B} означає «A{\displaystyle A} істинне тоді і тільки тоді, коли B{\displaystyle B} істинне». | x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y\,} |
| «тоді і тільки тоді» або «рівносильно» | ||||
| скрізь | ||||
| ∧{\displaystyle \wedge } | ∧ | Кон’юнкція | A∧B{\displaystyle A\wedge B} істинне тоді і тільки тоді, коли A{\displaystyle A} і B{\displaystyle B} обидва істині. | (n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, якщо n{\displaystyle n} — натуральне число. |
| «і» | ||||
| Математична логіка | ||||
| ∨{\displaystyle \vee } | ∨ | Диз’юнкція | A∨B{\displaystyle A\vee B} істинне, коли хоча б одна з умов A{\displaystyle A} або B{\displaystyle B} є істинною. | (n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, якщо n{\displaystyle n} — натуральне число. |
| «або» | ||||
| Математична логіка | ||||
| ¬{\displaystyle \neg } | ¬ | Заперечення | ¬A{\displaystyle \neg A} істинне тоді і тільки тоді, коли хибно A{\displaystyle A}. | ¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)} |
| «не» | ||||
| Математична логіка | ||||
| ∀{\displaystyle \forall } | ∀ | Квантор загальності | ∀x,P(x){\displaystyle \forall x,P(x)} означає «P(x){\displaystyle P(x)} істинне для всіх x{\displaystyle x}». | ∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n} |
| «Для будь-яких», «Для всіх» | ||||
| Математична логіка | ||||
| ∃{\displaystyle \exists } | ∃ | Квантор існування | ∃x,P(x){\displaystyle \exists x,\;P(x)} означає «існує хоча б одне x{\displaystyle x} таке, що P(x){\displaystyle P(x)} істинне» | ∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (підходить число 5) |
| «існує» | ||||
| Математична логіка | ||||
| ={\displaystyle =\,} | = | Рівність | x=y{\displaystyle x=y} означає «x{\displaystyle x} і y{\displaystyle y} означають один і той же об’єкт». | 1 + 2 = 6 − 3 |
| «дорівнює» | ||||
| скрізь | ||||
| :={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } =def{\displaystyle {\stackrel {\rm {def}}{=}}} | := :⇔ | Визначення | x:=y{\displaystyle x:=y} означає «x{\displaystyle x} за визначенням дорівнює y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означає «P{\displaystyle P} за визначенням рівносильно Q{\displaystyle Q}» | ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}(x):={1 \over 2}\left(e^{x}+e^{-x}\right)} (Гіперболічний косинус) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (Виключаюче або) |
| «дорівнює/рівносильно за визначенням» | ||||
| скрізь | ||||
| {,}{\displaystyle \{,\}} | { , } | Множина елементів | {a,b,c}{\displaystyle \{a,\;b,\;c\}} означає множина, елементами якої є a{\displaystyle a}, b{\displaystyle b} та c{\displaystyle c}. | N={0,1,2,…}{\displaystyle \mathbb {N} =\{0,\;1,\;2,\;\ldots \}} (множина натуральних чисел) |
| «Множина…» | ||||
| Теорія множин | ||||
| {|}{\displaystyle \{|\}} {:}{\displaystyle \{:\}} | { | } { : } | Множина елементів, що задовольняють умові | {x|P(x)}{\displaystyle \{x\,|\,P(x)\}} означає множину усіх x{\displaystyle x} таких, що істинне P(x){\displaystyle P(x)}. | {n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}} |
| «Множина всіх… таких, що істинне…» | ||||
| Теорія множин | ||||
| ∅{\displaystyle \varnothing } {}{\displaystyle \{\}} | ∅ {} | Порожня множина | {}{\displaystyle \{\}} і ∅{\displaystyle \varnothing } означає множину, що не містить жодного елементу. | {n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing } |
| «Порожня множина» | ||||
| Теорія множин | ||||
| ∈{\displaystyle \in } ∉{\displaystyle \notin } | ∈ ∉ | приналежність/неприналежність до множини | a∈S{\displaystyle a\in S} означає «a{\displaystyle a} є елементом множини S{\displaystyle S}» a∉S{\displaystyle a\notin S} означає «a{\displaystyle a} не є елементом S{\displaystyle S}» | 2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} } |
| «належить», «з» «не належить» | ||||
| Теорія множин | ||||
| ⊆{\displaystyle \subseteq } ⊂{\displaystyle \subset } | ⊆ ⊂ | Підмножина | A⊆B{\displaystyle A\subseteq B} означає «кожний елемент з A{\displaystyle A} також є елементом з B{\displaystyle B}». A⊂B{\displaystyle A\subset B} як правило означає те ж, що і A⊆B{\displaystyle A\subseteq B}. Однак деякі автори використовують ⊂{\displaystyle \subset }, щоб показати строге включення (а саме ⊊{\displaystyle \subsetneq }). | (A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} } |
| «є підмножиною», «включено в» | ||||
| Теорія множин | ||||
| ⊊{\displaystyle \subsetneq } | ⫋ | Власна підмножина | A⊊B{\displaystyle A\subsetneq B} означає A⊆B{\displaystyle A\subseteq B} і A≠B{\displaystyle A\neq B}. | N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} } |
| «є власною підмножиною», «строго включається в» | ||||
| Теорія множин | ||||
| ∪{\displaystyle \cup } | ∪ | Об’єднання | A∪B{\displaystyle A\cup B} означає множину елементів, що належать A{\displaystyle A} або B{\displaystyle B} (або обом одразу). | A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B} |
| «Об’єднання … і …», «…, об’єднане з …» | ||||
| Теорія множин | ||||
| ∩{\displaystyle \cap } | ⋂ | Перетин | A∩B{\displaystyle A\cap B} означає множину елементів, що належать і A{\displaystyle A}, і B{\displaystyle B}. | {x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}} |
| «Перетин … і … », «…, перетнуте з …» | ||||
| Теорія множин | ||||
| ∖{\displaystyle \setminus } | \ | Різниця множин | A∖B{\displaystyle A\setminus B} означає множину елементів, що належать A{\displaystyle A}, але не належать B{\displaystyle B}. | {1,2,3,4}∖{3,4,5,6}={1,2}{\displaystyle \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\}=\{1,\;2\}} |
| «різниця … і … », «мінус», «… без …» | ||||
| Теорія множин | ||||
| →{\displaystyle \to } | → | Функція | f:X→Y{\displaystyle f\!\!:X\to Y} означає функцію f{\displaystyle f}, що відображає множину (область визначення) X{\displaystyle X} у множину Y{\displaystyle Y}. | Функція f:Z→Z{\displaystyle f\!\!:\mathbb {Z} \to \mathbb {Z} }, що визначення як f(x)=x2{\displaystyle f(x)=x^{2}} |
| «з … в», | ||||
| скрізь | ||||
| ↦{\displaystyle \mapsto } | ↦ | Відображення | x↦f(x){\displaystyle x\mapsto f(x)} означає, що образом x{\displaystyle x} після застосування функції f{\displaystyle f} буде f(x){\displaystyle f(x)}. | Функцію, що визначення як f(x)=x2{\displaystyle f(x)=x^{2}}, можна записати так: f:x↦x2{\displaystyle f\colon x\mapsto x^{2}} |
| «відображується в» | ||||
| скрізь | ||||
| N{\displaystyle \mathbb {N} } | N або ℕ | Натуральні числа | N{\displaystyle \mathbb {N} } означає множину {1,2,3,…}{\displaystyle \{1,\;2,\;3,\;\ldots \}} або |
uk.wikipedia.org
Математический знаки и символы
«Символы не являются только записью мыслей,
средством её изображения и закрепления, –
нет, они воздействуют на самую мысль,
они… направляют её, и бывает достаточно
переместить их на бумаге… для того, чтобы
безошибочно достигнуть новых истин».
Л.Карно
Математические знаки служат в первую очередь для точной (однозначно определённой) записи математических понятий и предложений. Их совокупность в реальных условиях их применения математиками составляет то, что называется, математическим языком.
Математические знаки позволяют записывать в компактной форме предложения, громоздко выраженные на обычном языке. Это облегчает их запоминание.
Прежде чем использовать в рассуждениях те или иные знаки, математик старается сказать, что каждый из них обозначает. Иначе его могут не понять.
Но математики не всегда могут сказать сразу, что отражает тот или иной символ, введённый ими для какой-либо математической теории. Например, сотни лет математики оперировали отрицательными и комплексными числами, однако объективный смысл этих чисел и действие с ними удалось раскрыть лишь в конце XVIII и в начале XIX века.
1. Символизм математических кванторов
Подобно обычному языку, язык математических знаков позволяет обмениваться установленными математическими истинами, но являясь лишь вспомогательным средством, присоединяемым к обычному языку и без него существовать, не может.
Математическое определение:
На обычном языке:
Пределом функции F (x) в некоторой точке X0 называется постоянное число А, такое что для произвольного числа Е>0 существует такое положительное d(E), что из условия |X – X0|<d вытекает неравенство |F(x)–A|<E
Запись в кванторах (на математическом языке)
|
2. Символизм математических знаков и геометрических фигур.
1) Бесконечность — концепция, используемая в математике, философии и естественных науках. Бесконечность какого-то понятия или атрибута некоторого объекта означает невозможность указать для него границы или количественную меру. Термин бесконечность соответствует нескольким различным понятиям, в зависимости от области применения, будь то математика, физика, философия, теология или повседневная жизнь. В математике не существует одного понятия бесконечности, она наделяется особыми свойствами в каждом разделе. Более того, эти различные «бесконечности» не взаимозаменяемы. К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Скажем, количество целых чисел бесконечно большое (оно называется счётным). Чтобы обобщить понятие количества элементов для бесконечных множеств, в математике вводится понятие мощности множества. При этом не существует одной «бесконечной» мощности. Например, мощность множества действительных чисел больше мощности целых чисел, потому что между этими множествами нельзя построить взаимно-однозначное соответствие, а целые числа включены в действительные. Таким образом, в этом случае одно кардинальное число (равно мощности множества) «бесконечнее» другого. Основоположником этих понятий был немецкий математик Георг Кантор. В математическом анализе ко множеству действительных чисел добавляются два символа, плюс и минус бесконечность, применяющиеся для определения граничных значений и сходимости. Нужно отметить, что в этом случае речь об «осязаемой» бесконечности не идёт, так как любое утверждение, содержащее этот символ, можно записать, используя только конечные числа и кванторы. Эти символы (как и многие другие) были введены для сокращения записи более длинных выражений. Бесконечность также неразрывно связана с обозначением бесконечно малого, к примеру, ещё Аристотель сказал:
- время,
- разделение величин,
- неиссякаемость творящей природы,
- само понятие границы, толкающее за её пределы,
- мышление, которое неостановимо.
Бесконечность в большинстве культур появилась как абстрактное количественное обозначение чего-то непостижимо большого, в применении к сущностям без пространственных или временных границ.
Далее бесконечность получила развитие в философии и теологии наравне с точными науками. К примеру, в теологии бесконечность Бога не столько даёт количественное определение, сколько означает неограниченность и непостижимость. В философии это атрибут пространства и времени.
Современная физика вплотную подходит к отрицаемой Аристотелем актуальности бесконечности — то есть доступности в реальном мире, а не только в абстрактном. Например, есть понятие сингулярности, тесно связанное с чёрными дырами и теорией большого взрыва: это точка в пространстве—времени, в которой масса в бесконечно малом объёме сосредоточена с бесконечной плотностью. Уже есть солидные косвенные доказательства существования чёрных дыр, хотя теория большого взрыва находится ещё в стадии разработки.
2) Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку. Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
3) Квадрат (ромб) – является символом комбинации и упорядочивания четырёх различных элементов, например четыре основных стихий или четырёх времён года. Символ числа 4, равенства, простоты, прямоты, истины, справедливости, мудрости, чести. Симметрия является той идеей посредством которой человек пытается постичь гармонию и с давних времён считалась символом прекрасного. Симметрией обладают так называемые “фигурные” стихи, текст которых имеет очертание ромба.
Стихотворение – ромб.
Мы –
Среди тьмы.
Глаз отдыхает.
Сумрак ночи живой.
Сердце жадно вздыхает,
Шепот звёзд долетает порой.
И лазурные чувства теснятся толпой.
Всё забылось в блеске росистом.
Поцелуем душистым!
Поскорее блесни!
Снова шепни,
Как тогда:
«Да!»(Э.Мартов, 1894г)
4) Прямоугольник. Из всех геометрических форм это наиболее рациональная, наиболее надёжная и правильная фигура; эмпирически это объясняется тем фактом, что всегда и везде прямоугольник был излюбленной формой. С помощью него человек приспосабливал пространство или какой-либо предмет для непосредственного использования в своём быту, например: дом, комната, стол, кровать и т.п.
5) Пентагон – правильный пятиугольник в виде звезды символ вечности, совершенства, вселенной. Пентагон – амулет здоровья, знак на дверях для того, чтобы отогнать ведьм, эмблема Тота, Меркурия, кельтского Гавайна и др., символ пяти ран Иисуса Христа, благополучия, удачи у евреев, легендарный ключ Соломона; знак высокого положения в обществе у Японцев.
6) Правильный шестиугольник, гексагон – символ изобилия, красоты, гармонии, свободы, брака, символ числа 6, образ человека (две руки, две ноги, голова и туловище).
7) Крест – символ высших сакральных ценностей. Крест моделирует духовный аспект, восхождение духа, устремление к богу, к вечности. Крест – универсальный символ единства жизни и смерти.
Однако никто не будет отрицать, что любое изображение вызывает у человека ассоциации. Но проблема в том, что одни предметы, сюжеты или графические элементы вызывают у всех людей (вернее, у многих) одинаковые ассоциации, а другие – совершенно различные.
8) Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Свойства треугольника как фигуры: прочность, неизменяемость.
Аксиома А1 стереометрии гласит: «Через 3 точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна!»
Треугольник обычно относят к острой, «наступательной» фигуре, связанной с мужским началом. Равносторонний треугольник – мужской и солнечный знак, представляющий божество, огонь, жизнь, сердце, гору и восхождение, благополучие, гармонию и королевскую власть. Перевёрнутый треугольник – женский и лунный символ, олицетворяет воду, плодовитость, дождь, божественную милость.
9) Шестиконечная Звезда (Звезда Давида) – состоит из двух наложенных один на другой равносторонних треугольников. Одна из версий происхождения знака связывает его форму с формой цветка Белой лилии, имеющего шесть лепестков. Цветок традиционно располагался под храмовым светильником, таким образом, что священник зажигал огонь, как бы, в центре Маген Давида. В каббале два треугольника символизируют свойственную человеку дуальность: добро против зла, духовное против физического и так далее. Треугольник, направленный остриём вверх, символизирует наши добрые дела, которые поднимаются на небеса и вызывают поток благодати, нисходящий обратно в этот мир (что символизирует треугольник, направленный вниз). Иногда Звезду Давида называют Звездой Творца и связывают каждый из её шести концов с одним из дней недели, а центр – с субботой.
Государственные символы США также содержат Шестиконечную Звезду в разных видах, в частности есть она на Большой печати США и на денежных знаках. Звезда Давида изображена на гербах немецких городов Шер и Гербштедт, а так же украинских Тернополя и Конотопа. Три шестиконечные звезды изображены на флаге Бурунди и олицетворяют национальный девиз: «Единство. Работа. Прогресс».
В христианстве шестиконечная звезда – символ Христа, а именно соединения во Христе божественной и человеческой природы. Именно поэтому этот знак вписан в Православный Крест.
10) Пятиконечная Звезда – Основной отличительной эмблемой большевиков является красная пятиконечная звезда, официально установленная весной 1918 года. Первоначально большевистская пропаганда назвала её “ Марсовой звездой” ( якобы принадлежащей античному богу войны – марсу), а затем стала заявлять, что “ Пять лучей звезды, означает союз трудящихся всех пяти континентов в борьбе против капитализма”. В действительности же пятиконечная звезда не имеет никакого отношения ни к воинствующему божеству Марсу, ни к международному пролетариату, это – древний оккультный знак (очевидно ближневосточного происхождения), называющийся “пентаграммой” или &
urok.1sept.ru
Основные математические знаки и символы :: SYL.ru
Как известно, математика любит точность и краткость – недаром одна-единственная формула может в словесной форме занимать абзац, а порой и целую страницу текста. Таким образом, графические элементы, используемые во всем мире в науке, призваны увеличить скорость написания и компактность представления данных. Кроме того, стандартизованные графические изображения может распознать носитель любого языка, имеющий базовые знания в соответствующей сфере.
История математических знаков и символов насчитывает много столетий – некоторые из них были придуманы случайным образом и предназначались для обозначения иных явлений; другие же стали продуктом деятельности ученых, целенаправленно формирующих искусственный язык и руководствующихся исключительно практическими соображениями.
Плюс и минус
История происхождения символов, обозначающих простейшие арифметические операции, доподлинно неизвестна. Однако существует достаточно вероятная гипотеза происхождения знака «плюс», имеющего вид перекрещенных горизонтальной и вертикальной черт. В соответствии с ней символ сложения берет начало в латинском союзе et, который переводится на русский язык как «и». Постепенно, с целью ускорения процесса записи, слово было сокращено до вертикально ориентированного креста, напоминающего букву t. Самый ранний достоверный пример подобного сокращения датируется XIV веком.
Общепринятый знак «минус» появился, по всей видимости, позже. В XIV и даже XV веке в научной литературе использовался целый ряд символов, обозначающих операцию вычитания, и лишь к XVI веку «плюс» и «минус» в их современном виде стали встречаться в математических трудах вместе.Умножение и деление
Как ни странно, математические знаки и символы для этих двух арифметических действий не полностью стандартизованы и сегодня. Популярным обозначением умножения является предложенный математиком Отредом в XVII веке диагональный крестик, который можно увидеть, например, на калькуляторах. На уроках математики в школе ту же операцию обычно представляют в виде точки – данный способ предложил в том же веке Лейбниц. Ещё один способ представления – звёздочка, которая наиболее часто используется при компьютерном представлении различных расчётов. Использовать её предложил всё в том же XVII веке Иоганн Ран.
Для операции деления предусмотрены знак наклонной черты (предложен Отредом) и горизонтальная линия с точками сверху и снизу (символ ввел Иоганн Ран). Первый вариант обозначения является более популярным, однако второй также достаточно распространен.
Математические знаки и символы и их значения порой изменяются во времени. Однако все три способа графического представления умножения, а также оба способа для деления являются в той или иной степени состоятельными и актуальными на сегодняшний день.
Равенство, тождество, эквивалентность
Как и в случае многих других математических знаков и символов, обозначение равенства изначально было словесным. Достаточно продолжительное время общепринятым обозначением служило сокращение ae от латинского aequalis («равны»). Однако в XVI веке математик из Уэльса по имени Роберт Рекорд предложил в качестве символа две горизонтальные прямые, расположенные друг под другом. Как утверждал ученый, нельзя придумать ничего более равного между собой, чем два параллельных отрезка.
Несмотря на то что аналогичный знак использовался для обозначения параллельности прямых, новый символ равенства постепенно получил распространение. К слову, такие знаки как «больше» и «меньше», изображающие развернутые в разные стороны галочки, появились лишь в XVII-XVIII веке. Сегодня же они кажутся интуитивно понятными любому школьнику.Несколько более сложные знаки эквивалентности (две волнистые линии) и тождества (три горизонтальные параллельные прямые) вошли в обиход лишь во второй половине XIX века.
Знак неизвестного – «Икс»
История возникновения математических знаков и символов знает и весьма интересные случаи переосмысления графики по мере развития науки. Знак обозначения неизвестного, именуемый сегодня «иксом», берет своё начало на Ближнем Востоке на заре прошлого тысячелетия.
Ещё в X веке в арабском мире, славящемся в тот исторический период своими учеными, понятие неизвестного обозначалось словом, буквально переводящимся как «нечто» и начинающимся со звука «Ш». С целью экономии материалов и времени слово в трактатах стало сокращаться до первой буквы.
Спустя многие десятилетия письменные труды арабских ученых оказались в городах Пиренейского полуострова, на территории современной Испании. Научные трактаты стали переводиться на национальный язык, но возникла трудность — в испанском отсутствует фонема «Ш». Заимствованные арабские слова, начинающиеся с неё, записывались по особому правилу и предварялись буквой X. Научным языком того времени была латынь, в которой соответствующий знак имеет название «Икс».Таким образом, знак, на первый взгляд являющийся лишь случайно выбранным символом, имеет глубокую историю и изначально является сокращением арабского слова «нечто».
Обозначение других неизвестных
В отличие от «Икса», знакомые нам со школьной скамьи Y и Z, а также a, b, c имеют гораздо более прозаичную историю происхождения.
В XVII веке была издана книга Декарта под названием «Геометрия». В этой книге автор предлагал стандартизировать символы в уравнениях: в соответствии с его идеей, последние три буквы латинского алфавита (начиная от «Икса») стали обозначать неизвестные, а три первые – известные значения.
Тригонометрические термины
По-настоящему необычна история такого слова, как «синус».
Первоначально соответствующие тригонометрические функции получили название в Индии. Слово, соответствующее понятию синуса, буквально означало «тетива». В эпоху расцвета арабской науки индийские трактаты были переведены, а понятие, аналога которому не оказалось в арабском языке, транскрибировано. По стечению обстоятельств, то, что получилось на письме, напоминало реально существующее слово «впадина», семантика которого не имела никакого отношения к исходному термину. В результате, когда в 12 веке арабские тексты были переведены на латынь, возникло слово «синус», означающее «впадина» и закрепившееся в качестве нового математического понятия.
А вот математические знаки и символы для тангенса и котангенса до сих пор не стандартизованы – в одних странах их принято писать как tg, а в других – как tan.Некоторые другие знаки
Как видно из примеров, описанных выше, возникновение математических знаков и символов в значительной мере пришлось на XVI-XVII века. На этот же период пришлось возникновение привычных сегодня форм записи таких понятий, как процент, квадратный корень, степень.
Процент, т. е. сотая доля, долгое время обозначался как cto (сокращение от лат. cento). Считается, что общепринятый на сегодняшний день знак появился в результате опечатки около четырехсот лет назад. Получившееся изображение было воспринято как удачный способ сокращения и прижилось.
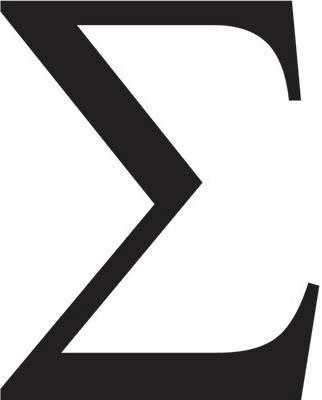Знак корня изначально представлял собой стилизованную букву R (сокращение от латинского слова radix — «корень»). Верхняя черта, под которую сегодня записывается выражение, выполняла функцию скобок и являлась отдельным символом, обособленным от корня. Круглые скобки были придуманы позже — в повсеместное обращение они вошли благодаря деятельности Лейбница (1646-1716). Благодаря его же трудам был введен в науку и символ интеграла, выглядящий как вытянутая буква S — сокращение от слова «сумма».Наконец, знак операции возведения в степень был придуман Декартом и доработан Ньютоном во второй половине XVII века.
Более поздние обозначения
Учитывая, что знакомые нам графические изображения «плюса» и «минуса» были введены в обращение всего несколько столетий назад, не кажется удивительным, что математические знаки и символы, обозначающие сложные явления, стали использоваться лишь в позапрошлом веке.
Так, факториал, имеющий вид восклицательного знака после числа или переменной, появился лишь в начале XIX века. Приблизительно тогда же появились заглавная «П» для обозначения произведения и символ предела.
Несколько странно, что знаки для числа Пи и алгебраической суммы появились лишь в XVIII веке – позже, чем, например, символ интеграла, хотя интуитивно кажется, что они являются более употребительными. Графическое изображение отношения длины окружности к диаметру происходит от первой буквы греческих слов, означающих «окружность» и «периметр». А знак «сигма» для алгебраической суммы был предложен Эйлером в последней четверти XVIII столетия.Названия символов на разных языках
Как известно, языком науки в Европе на протяжении многих веков была латынь. Физические, медицинские и многие другие термины часто заимствовались в виде транскрипций, значительно реже – в виде кальки. Таким образом, многие математические знаки и символы на английском называются почти так же, как на русском, французском или немецком. Чем сложнее суть явления, тем выше вероятность, что в разных языках оно будет иметь одинаковое название.
Компьютерная запись математических знаков
Простейшие математические знаки и символы в «Ворде» обозначаются обычной комбинацией клавиш Shift+цифра от 0 до 9 в русской или английской раскладке. Отдельные клавиши отведены под некоторые широкоупотребительные знаки: плюс, минус, равенство, наклонная черта.
Если же требуется использовать графические изображения интеграла, алгебраической суммы или произведения, числа Пи и т. д., требуется открыть в «Ворде» вкладку «Вставка» и найти одну из двух кнопок: «Формула» или «Символ». В первом случае откроется конструктор, позволяющий выстроить целую формулу в рамках одного поля, а во втором – таблица символов, где можно найти любые математические знаки.Как запомнить математические символы
В отличие от химии и физики, где количество символов для запоминания может превосходить сотню единиц, математика оперирует относительно небольшим числом знаков. Простейшие из них мы усваиваем ещё в глубоком детстве, учась складывать и вычитать, и только в университете на определенных специальностях знакомимся с немногочисленными сложными математическими знаками и символами. Картинки для детей помогают за считанные недели достичь мгновенного узнавания графического изображения требуемой операции, гораздо больше времени может понадобиться для овладения навыком самого осуществления этих операций и понимания их сущности.
Таким образом, процесс запоминания знаков происходит автоматически и не требует особых усилий.
В заключение
Ценность математических знаков и символов заключается в том, что их без труда понимают люди, говорящие на разных языках и являющиеся носителями различных культур. По этой причине крайне полезно понимать и уметь воспроизводить графические изображения различных явлений и операций.
Высокий уровень стандартизации этих знаков обуславливает их использование в самых различных сферах: в области финансов, информационных технологий, инженерном деле и др. Для каждого, кто хочет заниматься делом, связанным с числами и расчетами, знание математических знаков и символов и их значений становится жизненной необходимостью.
www.syl.ru
Символы Коды математические HTML | ||
Символы html | Код html | Описание спецсимволов html |
| − | − | Минус |
| ± | ± | Плюс-минус |
| × | × | Умножить |
| ÷ | ÷ | Разделить |
| < | < | Меньше |
| > | > | Больше |
| ≤ | ≤ | Меньше или равно |
| ≥ | ≥ | Больше или равно |
| π | π | Пи |
| √ | √ | Корень квадратный |
| ⁄ | ⁄ | Слэш, дробная черта |
| ¬ | ¬ | Отрицание |
| ∠ | ∠ | Угол |
| ° | ° | Градус |
| ∼ | ∼ | Оператор тильда |
| ≅ | ≅ | Геометрическая эквивалентность |
| ≈ | ≈ | Приблизительное равенство |
| ≠ | ≠ | Не равно |
| ≡ | ≡ | Тождественное равенство |
| | ||
| Дробь символы коды HTML | ||
| % | % | Простая дробь «ноль на ноль» |
| ¼ | ¼ | Дробь одна четвертая |
| ½ | ½ | Дробь одна вторая |
| ¾ | ¾ | Дробь три четвертых |
| ⅓ | ⅓ | Дробь одна третья |
| ⅔ | ⅔ | Дробь две третих |
| ⅕ | ⅕ | Дробь одна пятая |
| ⅖ | ⅖ | Дробь две пятых |
| ⅗ | ⅗ | Дробь три пятых |
| ⅘ | ⅘ | Дробь четыре пятых |
| ⅙ | ⅙ | Дробь одна шестая |
| ⅚ | ⅚ | Дробь пять шестых |
| ⅛ | ⅛ | Дробь одна восьмая |
| ⅜ | ⅜ | Дробь три восьмых |
| ⅝ | ⅝ | Дробь пять восьмых |
| ⅞ | ⅞ | Дробь семь восьмых |
| Другие символы коды HTML | ||
| ¹ | ¹ | Верхний индекс «1» |
| ² | ² | Верхний индекс «2» |
| ³ | ³ | Верхний индекс «3» |
| ∞ | ∞ | Бесконечность |
| ∝ | ∝ | Пропорционально |
| ⊥ | ⊥ | Ортогонально, перпендикуляр |
| ∴ | ∴ | Следовательно |
| ƒ | ƒ | Функция |
| ∫ | ∫ | Интеграл |
| ∂ | ∂ | Частный дифференциал |
| ∇ | ∇ | Оператор набла |
| ∀ | ∀ | Для всех |
| ∃ | ∃ | Существует |
| ∏ | ∏ | Знак произведения |
| ∑ | ∑ | Сумма последовательности |
| ∧ | ∧ | Логическое И (конъюнкция) |
| ∨ | ∨ | Логическое ИЛИ (дизъюнкция) |
| ∅ | ∅ | Пустой набор = диаметр |
| ∈ | ∈ | Принадлежит |
| ∉ | ∉ | Не принадлежит |
| ∋ | ∋ | Содержит |
| ∩ | ∩ | Пересечение |
| ∪ | ∪ | Объединение |
| ⊂ | ⊂ | Является подмножеством |
| ⊃ | ⊃ | Является надмножеством |
| ⊄ | ⊄ | Не является подмножеством |
| ⊆ | ⊆ | Является подмножеством либо эквивалентно |
| ⊇ | ⊇ | Является надмножеством либо эквивалентно |
www.rabotayvinter.net
Из истории математических символов | Социальная сеть работников образования
li{counter-increment:lst-ctn-kix_list_2-6}#doc4217080 .lst-kix_list_1-1>li:before{content:»\0025cb «}#doc4217080 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc4217080 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc4217080 .lst-kix_list_3-2>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_3-7>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «. «}#doc4217080 .lst-kix_list_1-2>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_6-6>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_8-6>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc4217080 .lst-kix_list_1-5>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc4217080 .lst-kix_list_6-3>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_6-7>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-0>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-3>li:before{content:»» counter(lst-ctn-kix_list_2-3,decimal) «. «}#doc4217080 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc4217080 .lst-kix_list_3-5>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_1-4>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_6-2>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_4-2>li:before{content:»\0025cf «}#doc4217080 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc4217080 .lst-kix_list_8-0>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_4-6>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_5-7>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_8-5>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_5-3>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc4217080 .lst-kix_list_4-1>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_4-5>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc4217080 .lst-kix_list_3-0>li:before{content:»\0025cf «}#doc4217080 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc4217080 .lst-kix_list_1-0>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc4217080 .lst-kix_list_7-6>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_4-3>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc4217080 .lst-kix_list_5-8>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc4217080 .lst-kix_list_1-8>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_5-4>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc4217080 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc4217080 .lst-kix_list_4-4>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_3-4>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_1-3>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_8-3>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_3-3>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-4>li:before{content:»\0025cf «}#doc4217080 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc4217080 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc4217080 .lst-kix_list_3-6>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_8-1>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_5-0>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_5-2>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc4217080 .lst-kix_list_6-4>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_6-0>li:before{content:»\0025cf «}#doc4217080 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc4217080 .lst-kix_list_6-1>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-5>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_6-8>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_3-8>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-2>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_4-0>li:before{content:»\0025cf «}#doc4217080 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc4217080 .lst-kix_list_4-7>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_8-4>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_1-6>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc4217080 .lst-kix_list_6-5>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-8>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_5-6>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_3-1>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_8-7>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc4217080 .lst-kix_list_8-2>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_1-7>li:before{content:»\0025a0 «}#doc4217080 .lst-kix_list_8-8>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc4217080 .lst-kix_list_7-7>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc4217080 .lst-kix_list_5-1>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-1>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_4-8>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_5-5>li:before{content:»\0025cf «}#doc4217080 .lst-kix_list_7-3>li:before{content:»\0025cf «}#doc4217080 ol{margin:0;padding:0}#doc4217080 .c13{vertical-align:top;width:366.8pt;border-style:solid;border-color:#000000;border-width:0.5pt;padding:0pt 5.4pt 0pt 5.4pt}#doc4217080 .c12{vertical-align:top;width:94pt;border-style:solid;border-color:#000000;border-width:0.5pt;padding:0pt 5.4pt 0pt 5.4pt}#doc4217080 .c7{line-height:1.5;text-indent:35.4pt;text-align:justify;direction:ltr}#doc4217080 .c9{line-height:1.5;text-align:justify;direction:ltr}#doc4217080 .c4{line-height:1.0;text-align:justify;direction:ltr}#doc4217080 .c22{list-style-type:none;margin:0;padding:0}#doc4217080 .c6{line-height:1.0;text-align:center;direction:ltr}#doc4217080 .c14{max-width:466.6pt;background-color:#ffffff;padding:45pt 56.6pt 56.7pt 72pt}#doc4217080 .c3{color:inherit;text-decoration:inherit}#doc4217080 .c8{line-height:1.0;direction:ltr}#doc4217080 .c29{padding-left:0pt;margin-left:36pt}#doc4217080 .c28{font-size:20pt;font-family:»Times New Roman»}#doc4217080 .c0{font-size:12pt;font-family:»Times New Roman»}#doc4217080 .c1{font-size:14pt;font-family:»Times New Roman»}#doc4217080 .c10{font-size:18pt;font-family:»Times New Roman»}#doc4217080 .c18{line-height:1.5;direction:ltr}#doc4217080 .c26{color:#111111}#doc4217080 .c16{height:43pt}#doc4217080 .c11{height:0pt}#doc4217080 .c5{height:11pt}#doc4217080 .c21{margin-right:18pt}#doc4217080 .c27{height:34pt}#doc4217080 .c30{margin-left:18pt}#doc4217080 .c19{height:35pt}#doc4217080 .c15{font-style:italic}#doc4217080 .c23{border-collapse:collapse}#doc4217080 .c25{font-size:8pt}#doc4217080 .c20{text-align:right}#doc4217080 .c2{font-weight:bold}#doc4217080 .c31{text-indent:35.4pt}#doc4217080 .c17{vertical-align:super}#doc4217080 .c24{font-size:18pt}#doc4217080 .title{padding-top:24pt;line-height:1.15;text-align:left;color:#000000;font-size:36pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt}#doc4217080 .subtitle{padding-top:18pt;line-height:1.15;text-align:left;color:#666666;font-style:italic;font-size:24pt;font-family:»Georgia»;padding-bottom:4pt}#doc4217080 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc4217080 p{color:#000000;font-size:11pt;margin:0;font-family:»Arial»}#doc4217080 h2{padding-top:24pt;line-height:1.15;text-align:left;color:#000000;font-size:24pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt}#doc4217080 h3{padding-top:18pt;line-height:1.15;text-align:left;color:#000000;font-size:18pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt}#doc4217080 h4{padding-top:14pt;line-height:1.15;text-align:left;color:#000000;font-size:14pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt}#doc4217080 h5{padding-top:12pt;line-height:1.15;text-align:left;color:#000000;font-size:12pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt}#doc4217080 h5{padding-top:11pt;line-height:1.15;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt}#doc4217080 h6{padding-top:10pt;line-height:1.15;text-align:left;color:#000000;font-size:10pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt}#doc4217080 ]]>МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
Работу выполнил
ученик 7-а класса
ГБОУ СОШ № 574
Балагин Виктор
2012-2013 уч.год
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
- Введение
Слово математика пришло к нам из древнегреческого, где μάθημα означало «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю. М.В.Ломоносов говорил: «Математика ум в порядок приводит». Одним словом, математика учит нас учиться приобретать знания.
Математика – это первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число 35 в виде нарисованных в ряд 35 палочек. Можно сказать, что 1 палочка – это первый математический символ.
Математическая «письменность», которую мы сейчас используем — от обозначений неизвестных буквами x, y, z до знака интеграла — складывалась постепенно. Развитие символики упрощало работу с математическими операциями и способствовало развитию самой математики.
С древнегреческого «символ» (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию.
С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.
2. Знаки сложения, вычитания
История математических обозначений начинается с палеолита. Этим временем датируются камни и кости с насечками, использовавшимися для счета. Наиболее известный пример — кость Ишанго. Знаменитая кость из Ишанго (Конго) датируемая примерно 20 тысяч лет до новой эры, доказывает, что уже в то время человек выполнял достаточно сложные математические операции. Насечки на кости использовались для сложения и наносились группами, символизируя сложения чисел.
В Древнем Египте была уже намного более продвинутая система обозначений. Например, в папирусе Ахмеса в качестве символа сложения используется изображение двух ног, идущих вперед по тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полуэллиптическую кривую для вычитания.
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. Происхождение этих символов неясно. Одна из версий — они ранее использовались в торговом деле как признаки прибыли и убытка.
Считается, так же, что наш знак происходит от одной из форм слова “et’’, которое по-латыни значит “и’’. Выражение a + b писалось на латыни так: a et b. Постепенно, из-за частого использования, от знака «et» осталось только » t » , которое, со временем превратилось в » + «. Первым человеком, который, возможно, использовал знак как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.
Обозначения вычитания были более запутанными, так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
Первое использование современного алгебраического знака “” относится к немецкой рукописи по алгебре 1481 г., которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: « » и « — » . Систематическое использование знаков « » и « — » для сложения и вычитания встречается у Иоганна Видмана. Немецкий математик Иоганн Видманн (1462-1498) первым использовал оба знака для пометок присутствия и отсутствия студентов на своих лекциях. Правда, есть сведения, что он «позаимствовал» эти знаки у малоизвестного профессора Лейпцигского университета. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и , в труде «Быстрый и приятный счёт для всех торговцев» (ок. 1490)
Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ. Видман сам ввел его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест « † », иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид « ».
3.Знак равенства
Знак равенства в математике и других точных науках пишут между двумя идентичными по своему размеру выражениями. Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный). В античной и средневековой математике равенство обозначалось словесно, например, est egale, или использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые буквы слова “равный’’, но это не было общепринятым. Знак равенства «=» ввел в 1557 году уэльский врач и математик Роберт Рекорд (Recorde R., 1510-1558). Математическим символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя одинаковыми горизонтальными параллельными отрезками, гораздо более длинными, чем те, что используются сегодня. Английский математик Роберт Рекорд был первым, кто начал использовать символ «равенство», аргументируя словами: «никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». Но ещё в XVII веке Рене Декарт использовал аббревиатуру “ae’’. Франсуа Виет знаком равенства обозначал вычитание. Некоторое время распространению символа Рекорда мешало то обстоятельство, что такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным. Распространение знак получил только после работ Лейбница на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда. На его могильной плите нет слов – просто вырезан знак «равно».
Родственные символы для обозначения приблизительного равенства «≈» и тождества «≡» являются совсем молодыми — первый введен в 1885 году Гюнтером, второй — в 1857 году Риманом
4. Знаки умножения и деления
Знак умножения в виде крестика («х») ввел англиканский священник-математик Уильям Отред в 1631 году. До него для знака умножения использовали букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон, 1634), звёздочка (Иоганн Ран, 1659).
Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Для обозначения действия деления Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. Деление в виде обелюс («÷») ввел швейцарский математик Иоганн Ран (ок. 1660)
5. Знак процента.
Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта (1685). В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
6.Знак бесконечности
Нынешний символ бесконечности «∞» ввел в употребление Джон Уоллис в 1655 году. Джон Уоллис издал большой трактат «Арифметика бесконечного» (лат. Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque Difficiliora Matheseos Problemata), где ввёл придуманный им символ бесконечности. До сих пор так и не известно, почему он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных гипотез связывает происхождение этого символа с латинской буквой «М», которую римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента) математиком Бернулли приблизительно сорок лет спустя.
Другая версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия «бесконечность»: движение без конца. По линиям числа 8 можно совершать, как по велотреку, бесконечное движение. Для того, чтобы не путать введенный знак с числом 8, математики решили располагать его горизонтально. Получилось . Такое обозначение cтало стандартным для всей математики, не только алгебры. Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не поворачивай — она не изменится. Поэтому выбор и пал именно на 8.
Другой вариант — змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца.
Многие считают, что лист Мёбиуса является прародителем символа бесконечности, т.к символ бесконечности был запатентован после изобретения устройства «лента Мебиуса» (названный в честь математика девятнадцатого столетия Мебиуса). Лента Мебиуса — полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Однако по имеющимся историческим сведениям символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса
7. Знаки угла и перпендикулярности
Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон. Символ перпендикулярности у него был перевёрнут, напоминая букву T. Символ угла напоминал значок , современную форму ему придал Уильям Отред (1657).
8. Знак параллельности
Символ «параллельности» известен с античных времён, его использовали Герон и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально (Отред (1677), Керси (John Kersey) и др. математики XVII века).
9. Число пи
Общепринятое обозначение числа, равного отношению длины окружности к ее диаметру (3,1415926535…), впервые образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια —окружность и περίμετρος — периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.
10. Синус и косинус
Интересно появление синуса и косинуса.
Sinus с латинского — пазуха, впадина. Но история у такого названия долгая. Далеко в тригонометрии продвинулись индийские математики в районе 5 века. Самого слова «тригонометрия» не было, оно было введено Георгом Клюгелем в 1770 году.) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для краткости называли просто — джия (тетива). Когда арабы переводили работы индусов с санскрита, они не стали переводить «тетиву» на арабский, а просто транскрибировали слово арабскими буквами. Получилась джиба. Но так как в слоговой арабской письменности краткие гласные не обозначаются, то реально остается дж-б, что похоже на другое арабское слово — джайб (впадина, пазуха). Когда Герард Кремонский в 12 веке переводил арабов на латынь, он перевел это слово как sinus, что по-латыни также означает пазуху, углубление.
Косинус появился автоматически, т.к. индусы называли его коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука на санскрите. Современные краткие обозначения и введены Уильямом Отредом и закреплены в трудах Эйлера.
Обозначения тангенса/котангенса имеют намного более позднее происхождение (английское слово tangent происходит от латинского tangere — касаться). И даже до сих пор нет унифицированного обозначения — в одних странах чаще используется обозначение tan, в других — tg
11. Сокращение «Что и требовалось доказать» (ч.т.д.)
«Quod erat demonstrandum» (квол эрат лэмонстранлум).
Греческая фраза имеет значение «что требовалось доказывать», а латинская — «что нужно было показать». Этой формулой заканчивается каждое математическое рассуждение великого греческого математика Древней Греции Эвклида (III в. до н. э.). В переводе с латинского — что и требовалось доказать. В средневековых научных трактатах эту формулу писали часто в сокращенном виде: QED.
12. Математические обозначения.
Символы | История символов |
+ — | Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии. |
× ∙ | Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621). |
/ : ÷ | Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века. |
= | Знак равенства предложил Роберт Рекорд (1510—1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем. |
Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше. | |
% | Символ процента появляется в середине XVII века сразу в нескольких источниках, его происхождение неясно. Есть гипотеза, что он возник от ошибки наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более вероятно, что это скорописный коммерческий значок, возникший лет на 100 раньше. |
√ | Знак корня впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы слова radix (корень). Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня. |
an | Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676). |
( ) | Скобки появились у Тартальи (1556) для подкоренного выражения, но большинство математиков предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц. |
Σ | Знак суммы ввёл Эйлер в 1755 году |
П | Знак произведения ввёл Гаусс в 1812 году |
i | Букву i как код мнимой единицы: предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый). |
π | Общепринятое обозначение числа 3.14159… образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр, то есть длина окружности. |
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). | |
y’ | Краткое обозначение производной штрихом восходит к Лагранжу. |
Символ предела появился в 1787 году у Симона Люилье (1750—1840). | |
Символ бесконечности придумал Валлис, опубликован в 1655 году. |
13. Заключение
Математическая наука необходима для цивилизованного общества. Математика содержится во всех науках. Математический язык смешивается с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые создают новые технологии. Сохранившиеся открытия дают возможность решать сложные математически задачи. И древний математический язык нам понятен, а открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли физические законы. Мы изучаем их в школе. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение математики необходимо для новых открытий.
Литература.
1.Что? Зачем? Почему? Большая книга вопросов и ответов. Пер.Мишиной К., А Зыковой -М: Издательство ЭКСМО, 2007
2. Глейзер Г.И. История математики в школе VII-VIII кл. Пособие для учителей. М: Просвещение, 1982
3. Рыбников К.А. История математики. Издательство Московского Университета, 1974
4. Интернет. www математические символы.
nsportal.ru
Математические знаки и символы: список, таблица, история возникновения
Когда люди долгое время взаимодействуют в рамках определенной сферы деятельности, они начинают искать способ оптимизировать процесс коммуникации. Система математических знаков и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл.
Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.
В соответствии с запросами общества графические символы для более простых математических операций (например, обозначение сложения и вычитания) были выработаны раньше, чем для сложных понятий наподобие интеграла или дифференциала. Чем сложнее понятие, тем более сложным знаком оно обычно обозначается.
Модели образования графических обозначений
На ранних этапах развития цивилизации люди связывали простейшие математические операции с привычными для них понятиями на основе ассоциаций. Например, в Древнем Египте сложение и вычитание обозначались рисунком идущих ног: направленные по направлению чтения строки они обозначали «плюс», а в обратную сторону – «минус».
Цифры, пожалуй, во всех культурах изначально обозначались соответствующим количеством черточек. Позже для записи стали использоваться условные обозначения — это экономило время, а также место на материальных носителях. Часто в качестве символов использовались буквы: такая стратегия получила распространение в греческом, латинском и многих других языках мира.
История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.Преобразование словесного представления
Изначально любое математическое понятие выражается некоторым словом или словосочетанием и не имеет собственного графического представления (помимо лексического). Однако выполнение расчетов и написание формул словами – процедура длительная и занимающая неоправданно много места на материальном носителе.
Распространенный способ создания математических символов – трансформация лексического представления понятия в графический элемент. Иначе говоря, слово, обозначающее понятие, с течением времени сокращается или преобразуется каким-либо другим способом.
Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.Другой пример – знак «икс», обозначающий неизвестное, который изначально представлял собой сокращение от арабского слова «нечто». Сходным образом произошли знаки для обозначения квадратного корня, процента, интеграла, логарифма и др. В таблице математических символов и знаков можно встретить более десятка графических элементов, появившихся таким образом.
Назначение произвольного символа
Второй распространенный вариант образования математических знаков и символов – назначение символа произвольным образом. В этом случае слово и графическое обозначение между собой не связаны — знак обычно утверждается в результате рекомендации одного из членов научного сообщества.
Например, знаки умножения, деления, равенства были предложены математиками Уильямом Отредом, Иоганном Раном и Робертом Рекордом. В некоторых случаях несколько математических знаков могли быть введены в науку одним ученым. В частности, Готфрид Вильгельм Лейбниц предложил целый ряд символов, в том числе интеграла, дифференциала, производной.
Простейшие операции
Такие знаки, как «плюс» и «минус», а также символы, обозначающие умножение и деление, знает каждый школьник, несмотря на то, что для последних двух упомянутых операций существует несколько возможных графических знаков.
Можно с уверенностью говорить, что складывать и вычитать люди умели ещё за много тысячелетий до нашей эры, а вот стандартизованные математические знаки и символы, обозначающие данные действия и известные нам сегодня, появились лишь к XIV-XV столетию.
Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).Латинские буквы
На протяжении многих столетий научное сообщество использовало для обмена информацией исключительно латынь, и многие математические термины и знаки обнаруживают свои истоки именно в этом языке. В некоторых случаях графические элементы стали результатом сокращения слов, реже – их намеренного или случайного преобразования (например, вследствие описки).
Обозначение процента («%»), вероятнее всего, происходит от ошибочного написания сокращения cto (cento, т. е. «сотая доля»). Сходным образом произошёл знак «плюс», история которого описана выше.
Гораздо большее количество символов было образовано путём намеренного сокращения слова, хотя это не всегда очевидно. Далеко не каждый человек узнает в знаке квадратного корня букву R, т. е. первый знак в слове Radix («корень»). Символ интеграла также представляет собой первую букву слова Summa, однако интуитивно она похожа на прописную f без горизонтальной черты. К слову, в первой публикации издатели совершили именно такую ошибку, напечатав f вместо данного символа.
Греческие буквы
В качестве графических обозначений для различных понятий используются не только латинские, но и греческие буквы. В таблице математических символов можно найти целый ряд примеров такого наименования.
Число Пи, представляющее собой отношение длины окружности к её диаметру, произошло от первой буквы греческого слова, обозначающего окружность. Существует ещё несколько менее известных иррациональных чисел, обозначаемых буквами греческого алфавита.
Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.Более того, практически все греческие буквы так или иначе используются в математике. Однако данные математические знаки и символы и их значение знают только люди, занимающиеся наукой профессионально. В быту и повседневной жизни эти знания человеку не требуются.
Знаки логики
Как ни странно, многие интуитивно понятные символы были придуманы совсем недавно.
В частности, горизонтальная стрелка, заменяющая слово «следовательно», была предложена лишь в 1922 года Давидом Гильбертом. Кванторы существования и всеобщности, т. е. знаки, читающиеся как: «существует…» и «для любого…», были введены в 1897 и 1935 году соответственно.
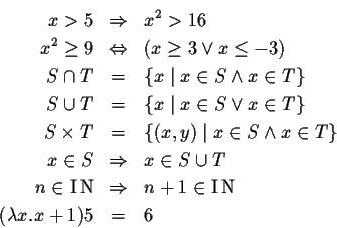Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.Таким образом, знаки для столь непростых понятий, как интеграл или логарифм, были придуманы на столетия раньше, чем некоторые интуитивно понятные символы, легко воспринимаемые и усваиваемые даже без предварительной подготовки.
Математические символы на английском
Ввиду того, что значительная часть понятий была описана в научных трудах на латыни, ряд названий математических знаков и символов на английском и русском языке одинаковы. Например: Plus («плюс»), Integral («интеграл»), Delta function («дельта-функция»), Perpendicular («перпендикулярный»), Parallel («параллельный»), Null («нуль»).
Часть понятий в двух языках называются различным образом: так, деление – это Division, умножение – Multiplication. В редких случаях английское название для математического знака получает некоторое распространение в русском языке: например, косая черта в последние годы нередко именуется «слешем» (англ. Slash).
Таблица символов
Самый простой и удобный способ ознакомиться с перечнем математических знаков – посмотреть специальную таблицу, в которой содержатся знаки операций, символы математической логики, теории множеств, геометрии, комбинаторики, математического анализа, линейной алгебры. В данной таблице представлены основные математические знаки на английском языке.
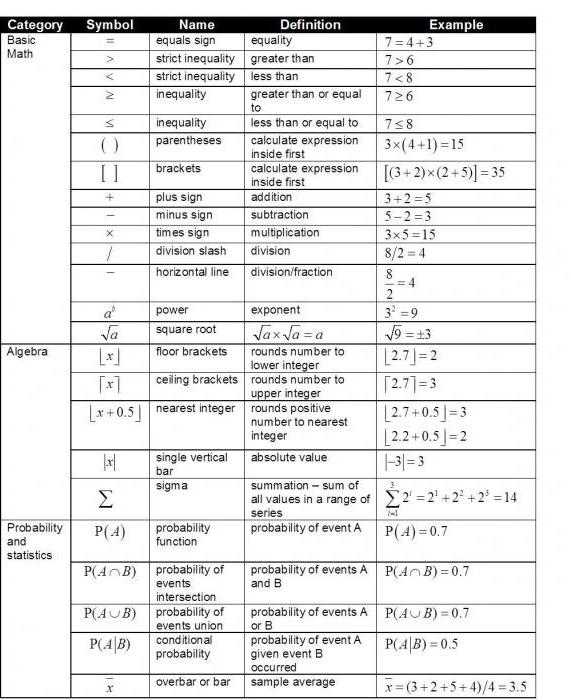
Математические знаки в текстовом редакторе
При выполнении различного рода работ зачастую требуется использовать формулы, где употребляются знаки, отсутствующие на клавиатуре компьютера.
Как и графические элементы из практически любой области знаний, математические знаки и символы в «Ворде» можно найти во вкладке «Вставка». В версиях программы 2003 или 2007 года существует опция «Вставка символа»: при нажатии на кнопку в правой части панели пользователь увидит таблицу, в которой представлены все необходимые математические знаки, греческие строчные и прописные буквы, различные виды скобок и многое другое.
В версиях программы, вышедших после 2010 года, разработана более удобная опция. При нажатии на кнопку «Формула» происходит переход в конструктор формул, где предусмотрено использование дробей, занесения данных под корень, смена регистра (для обозначения степеней или порядковых номеров переменных). Здесь же могут быть найдены все знаки из таблицы, представленной выше.
Стоит ли учить математические символы
Система математических обозначений представляет собой искусственный язык, который лишь упрощает процесс записи, но не может принести понимание предмета стороннему наблюдателю. Таким образом, запоминание знаков без изучения терминов, правил, логических связей между понятиями не приведет к овладению данной областью знаний.
Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.В заключение
Поскольку любой язык, в том числе искусственный, является открытым к изменениям и дополнениям, число математических знаков и символов непременно будет расти с течением времени. Не исключено, что какие-то элементы будут заменены или скорректированы, а другие – стандартизованы в единственно возможном виде, что актуально, например, для знаков умножения или деления.
Умение пользоваться математическими символами на уровне полного школьного курса является в современном мире практически необходимым. В условиях бурного развития информационных технологий и науки, повсеместной алгоритмизации и автоматизации владение математическим аппаратом следует воспринимать как данность, а освоение математических символов – как неотъемлемую его часть.
Поскольку расчеты используются и в гуманитарной сфере, и в экономике, и в естественных науках, и, разумеется, в области техники и высоких технологий, понимание математических понятий и знание символов станет полезным для любого специалиста.
fb.ru
| Символ (Символ (Unicode) | Название | Значение | Пример | |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ | Импликация, следование | означает «если A верно, то B также верно». Иногда вместо него используют . | верно, но неверно (так как x = − 2 также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает «A верно тогда и только тогда, когда B верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда A и B оба истинны. | , если n — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий A и B истинно. | , если n — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно A. | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает «P(x) верно для всех x». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один x такой, что верно P(x)» | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | x = y обозначает «x и y обозначают один и тот же объект». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| : = | := :⇔ | Определение | x: = y означает «x по определению равен y». означает «P по определению равносильно Q» | (Гиперболический косинус) (Исключающее или) |
| «равно/равносильно по определению» | ||||
| везде | ||||
| {,} | { , } | Множество элементов | означает множество, элементами которого являются a, b и c. | (множество натуральных чисел) |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } {:} | { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех x таких, что верно P(x). | |
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
{} | ∅ {} | Пустое множество | {} и означают множество, не содержащее ни одного элемента. | |
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает «a является элементом множества S» означает «a не является элементом множества S» | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из A также являестя элементом из B». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⫋ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих A или B (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и A, и B. | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих A, но не принадлежащих B. | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию f с областью определения X и областью прибытия Y. | Функция , определённая как f(x) = x2 | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом x после применения функции f будет f(x). | Функцию, определённую как f(x) = x2, можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | (i — комплексное число: i2 = − 1) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | x < y обозначает, что x строго меньше y. x > y означает, что x строго больше y. | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что x меньше или равен y. означает, что x больше или равен y. | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до 10 − 3 означает, что 2,718 отличается от e не больше чем на 10 − 3. | с точностью до 10 − 7. | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает положительное действительное число, которое в квадрате даёт x. | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину x. | A | обозначает мощность множества A и равняется, если A конечно, числу элементов A. | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма ak, где k принимает значения от 1 до n», то есть . означает сумму ряда, состоящего из ak. | = 12 + 22 + 32 + 42 = 30 | |
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение ak для всех k от 1 до n», то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ∫ | Интеграл | означает «интеграл от a до b функции f от x по переменной x». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
f‘(x) | df/dx f'(x) | Производная | или f‘(x) означает «(первая) производная функции f от x по переменной x». | |
| «Производная … по …» | ||||
| Математический анализ | ||||
f(n)(x) | dnf / dxn f(n)(x) | Производная n-го порядка | или f(n)(x) (во втором случае если n — фиксированное число, то оно пишется римскими цифрами) означает «n-я производная функции f от x по переменной x». | |
| «n-я производная … по …» | ||||
| Математический анализ |
biograf.academic.ru