Знаки больше меньше в какую сторону пишутся?
Доброго времени суток, уважаемые родители и маленькие школьники! Сегодня спешу поделиться с вами своим открытием. Недавно нашла в интернете, уже не помню точно где, решение проблемы, которая частенько подстерегает дошколят и учеников 1-х классов, которые только начинают свое знакомство с математикой.
Статья адресована всем тем, кого одолевает вопрос: «Знаки больше меньше в какую сторону пишутся?» Больше это как? Уголочком налево? Или направо? А может быть, это не больше, а меньше? Вспомните родители, у вас в школе были проблемы с этими коварными значками? И как вам объяснял эту тему учитель?
Если честно, я не помню, как объясняли мне, но точно не так, как я вам собираюсь показать. Все гениальное просто!
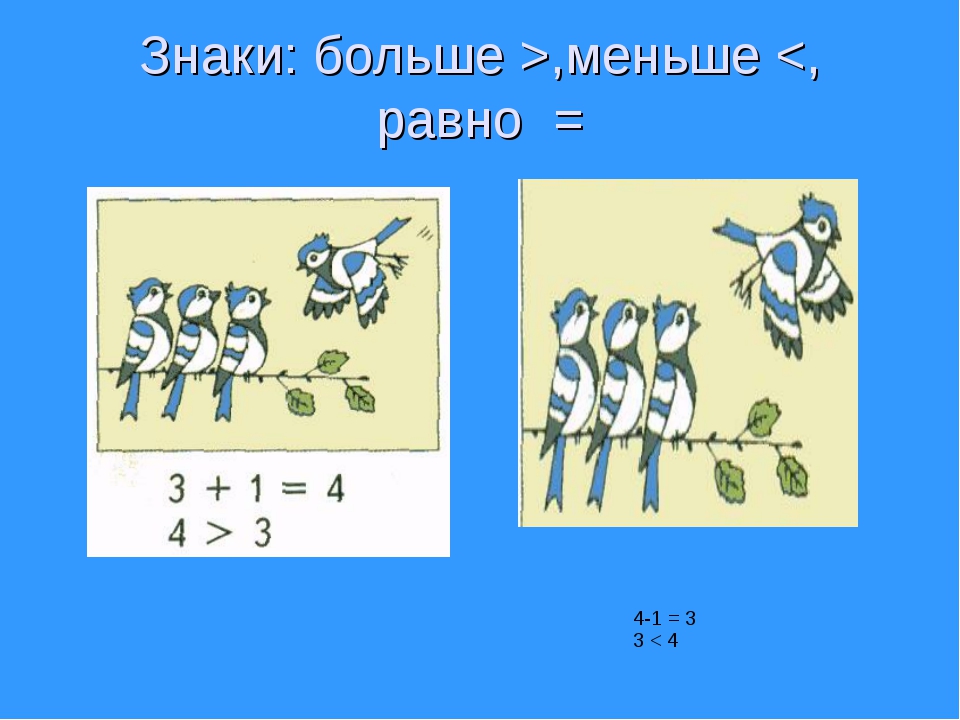
Давайте для начала посмотрим на исследуемые в статье знаки. Это «больше». Вот он, в примере на картинке.
Он ставится, когда первое число в неравенстве больше второго. Острие галочки направлено вправо.
А это его товарищ – «меньше».
Ставим его тогда, когда первое число неравенства (то, что левее) меньше, чем второе. Уголочек галочки направлен влево.
Вроде, все понятно, но в светлых головах наших маленьких школьников возникает путаница. Давайте на пример посмотрим. Вот какой знак сюда нужно поставить?
Дети наши — не глупые ребята. Они прекрасно знают, что тройка меньше шестерки. И значит, знак нужно ставить «меньше». Вот только, как он выглядит? Уголочек куда направлен: влево, вправо? Вот в этом месте и случается основной ступор. Ну как же запомнить-то?
И вот мы переходим к главному секрету! Нам поможет метод точек!!! Только посмотрите, как все просто. Внимание на картинку.
У нас два числа, которые необходимо сравнить. Мы понимаем, что, к примеру, число 8 меньше, чем 9. Около меньшего числа (восьмерочки) ставим одну точечку, так, как на картинке, а около большего (девяточки) — две. А потом просто соединяем эти точки, получаем нужный знак! И дело в шляпе!
Еще раз попробуем.
Согласитесь, очень просто! И понятно! И намного легче, нежели рассказы про раскрытые клювики голодных птичек или острие стрелы направленное на меньшее число.
Надеюсь, вам пригодится этот способ запоминания, и детишки никогда не будут снова ошибаться!
А может, вы тоже какой-нибудь секретик знаете? Напишите о нем в комментариях. Давайте делиться полезностями!
Кстати, мы уже говорили о том, как запоминать падежи.
Научились умножать на 9 с помощью пальчиков.
И узнали высокоскоростной способ деления на 5.
Посмотрите, это очень интересно! И наверняка пригодится в учебе.
Пожалуйста, не забудьте подписаться на новости блога, чтобы всегда быть в курсе наших событий. И вступайте в нашу группу «ВКонтакте», будем вам очень рады!
Успехов вам!
Ваша «ШколаЛа»
Математика для блондинок: Знак больше и меньше
Здесь мы рассмотрим элемент математического неравенства, при помощи которого в математике обычно выражается несправедливость. Если знак равенства можно считать отражением справедливости, то знаки «больше» и «меньше» отражают отсутствие таковой. Справедливость — это понятие относительное. То, что я считаю справедливым по отношению к вам, вы можете считать не справедливым по отношению к себе. И наоборот. То, что считаете справедливым вы, другие могут называть вопиющей несправедливостью. Каждый смотрит со своей колокольни. В математике всё это можно выразить при помощи знаков «больше» и «меньше».
Если знак равенства можно считать отражением справедливости, то знаки «больше» и «меньше» отражают отсутствие таковой. Справедливость — это понятие относительное. То, что я считаю справедливым по отношению к вам, вы можете считать не справедливым по отношению к себе. И наоборот. То, что считаете справедливым вы, другие могут называть вопиющей несправедливостью. Каждый смотрит со своей колокольни. В математике всё это можно выразить при помощи знаков «больше» и «меньше».Наблюдая за процессом сравнения со стороны, мы будем получать разные результаты в зависимости от того, в каком порядке мы выполняем сравнение. Небоскреб БОЛЬШЕ хибарки. Хибарка МЕНЬШЕ небоскреба. Как видите, результат сравнения зависит от того, что мы ставим на первое место при сравнении.
В математике неравенство возникает из-за того, что при записи математических выражений принят определенный порядок выписывания символов на бумаге. При этом один из символов обязательно будет на первом месте, второй символ — на втором.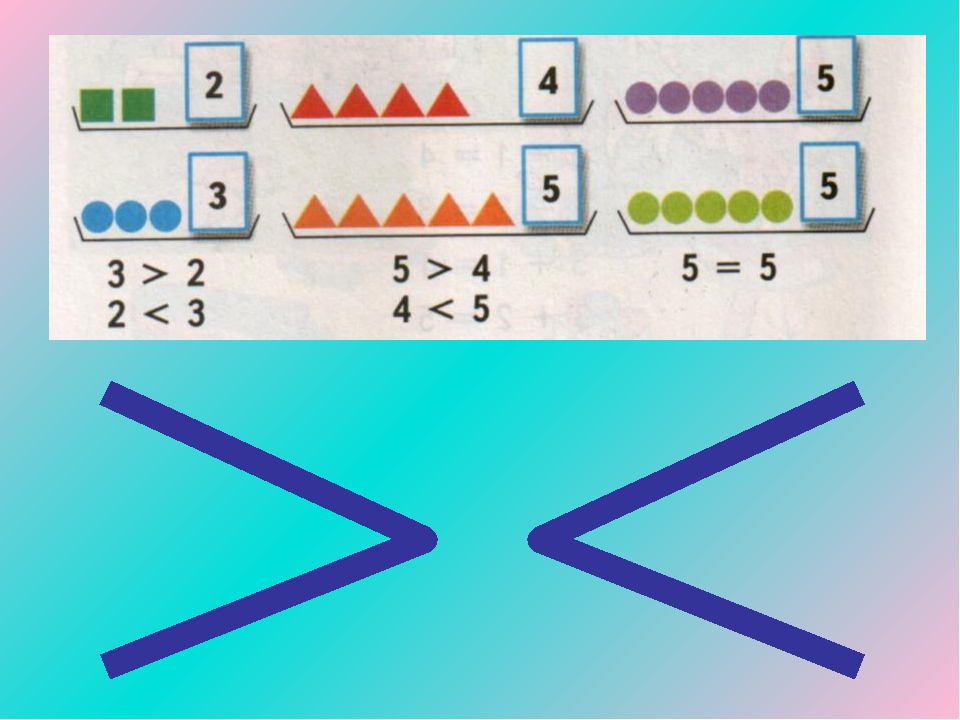 Это приводит к определенному результату при сравнении того, что эти символы обозначают. Если мы изменим порядок записи символов, то есть второй символ запишем на первом месте, а первый — после него, тогда у нас изменится результат сравнения. Математики очень удачно подобрали графические символы для обозначения понятий «больше» и «меньше». Вот смотрите.
Это приводит к определенному результату при сравнении того, что эти символы обозначают. Если мы изменим порядок записи символов, то есть второй символ запишем на первом месте, а первый — после него, тогда у нас изменится результат сравнения. Математики очень удачно подобрали графические символы для обозначения понятий «больше» и «меньше». Вот смотрите.
Что такое неравенство? Это почти то же самое, что и уравнение. Решаются они практически одинаково. Единственное, о чем нужно помнить при решении неравенств, что знаки «больше» и «меньше» могут выворачиваться на изнанку, а знак равенства — нет. Собственно, знак равенства тоже можно вывернуть, но никаких отличий вы не увидите. Другое дело со знаками «больше» и «меньше». Если такой знак вывернуть на изнанку, тогда его нос будет смотреть в другую сторону.
Никакой шаманской магии в этом нет. Обыкновенная относительность или, как её ещё называют в математике, зеркальная симметрия.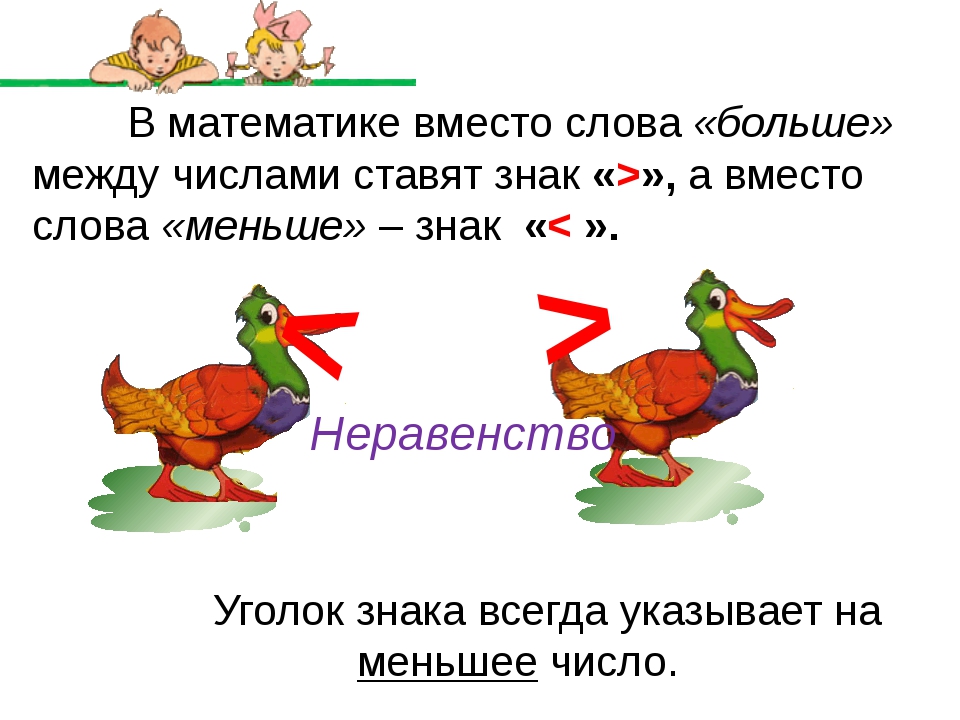
Нижняя половина рисунка является зеркальным отражением верхней половины. Или наоборот. Теперь возьмите зеркало. Приставьте его перпендикулярно к экрану монитора так, чтобы одновременно видеть картинку на экране монитора и её отражение в зеркале. В зеркале нижняя и верхняя половины картинки поменяются местами. Если бы не надпись на картинке «математика для блондинок», то вообще нельзя было бы точно сказать, где сама картинка, а где её отражение. Кстати, применение на уроках математики прозрачной стеклянной доски, вращающейся вокруг вертикальной оси, поможет понять очень многие вещи в математике.
Нужно помнить, что если мы переносим всего один элемент из одной части неравенства в другую и при этом МЕНЯЕМ ЗНАК «плюс» или «минус», то знак неравенства «больше» или «меньше» остается неизменным. Всё, как в уравнении. Если при переносе математического элемента через знак сравнения мы изменяем знак, результат сравнения не изменяется: равенство сохраняется, знак «больше» остается знаком «больше», знак «меньше» остается знаком «меньше».
Учим с дошкольниками знаки «больше», «меньше» или «равно».
Ваш ребенок уже хорошо сравнивает предметы по количеству? Он может соотнести не только множества предметов, но и цифры до 10? Пришло время его знакомить с символами «больше», «меньше», «равно». Приведем несколько идей, как облегчить сравнение «больше», «меньше» и «равно», поскольку дошкольники их часто путают.
Начните заниматься математикой онлайн прямо сейчас
- Пасть голодного крокодила.
 Нарисуйте два круга – две тарелки. Внутри каждой — множества предметов, которые надо сравнить. Рядом напишите знаки «больше» и «меньше». Попросите ребенка представить, что каждый из знаков – рот крокодила, указывающий в определённую сторону. Голодный крокодил наверняка выберет тарелку с большим количеством пищи, поэтому его пасть будет широко открыта возле этой тарелки. Это и есть знак «больше». Можно сравнивать и с клювом птички, если ребенку по душе такое сравнение.
Нарисуйте два круга – две тарелки. Внутри каждой — множества предметов, которые надо сравнить. Рядом напишите знаки «больше» и «меньше». Попросите ребенка представить, что каждый из знаков – рот крокодила, указывающий в определённую сторону. Голодный крокодил наверняка выберет тарелку с большим количеством пищи, поэтому его пасть будет широко открыта возле этой тарелки. Это и есть знак «больше». Можно сравнивать и с клювом птички, если ребенку по душе такое сравнение.
- Графический способ. Если написать знаки > и <, то мы увидим, что у одного расстояние слева между линиями больше, значит этот символ и есть «больше», у второго – меньше, значит это «меньше».
- Правая рука, левая рука. Сложите большой и указательный пальцы правой руки в форме уголка, получится знак «больше». Точно также пальцы левой руки образуют знак «меньше». Осталось запомнить: правая рука– больше, левая рука – меньше.
Знак «равно» обычно не предоставляет сложности для запоминания.
Можно практиковаться в сравнении предметов «больше», «меньше» либо «равно» на улице. В таком случае в качестве символов используйте палочки от мороженого или веточки. Уверены, что перечисленные способы запоминания облегчат изучение обозначений «больше» и «меньше», и не смотря на то, что они пишутся практически одинаково, ваш ребенок не будет их путать.
Хотите больше онлайн заданий? Начните заниматься прямо сейчас
Знаки больше и меньше в математике — сравнение чисел с примерами
Знаки больше и меньше в математике становятся известны детям еще до поступления в первый класс. Часто детки путают, что означает конкретный символ. Родители могут помочь своим чадам в этом вопросе, что положительно повлияет на успеваемость детей. Эти знания пригодятся малышам и в будущем – при изучении геометрии, на уроках алгебры, в примерах, где используется квадратная, а также другая степень чисел. Советы из дан статьи помогут родителям научить малышей важной математической премудрости.
Математические знаки в картинках для дошкольников
Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.
Знак «больше» – в какую сторону
Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».
Знак «меньше» – как правильно писать
Знак «меньше» выглядит так «<». Если сказать просто, то стрелка должна смотреть влево. И снова для определения важна левая часть стрелки. Если точка, из которой выходят две линии, расположена слева, то это символ «<».
Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «<» и одной линии.
Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.
Примеры на сравнение чисел для 1 класса
В первом блоке примеров (Таблица 1) нужно поставить правильный символ. Справа и слева стоят только однозначные числа.
Второй блок примеров (Таблица 2) содержит примеры, в которых нужно сопоставить суммы чисел. В случае равенства необходимо вписать знак «равно».
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «<» примерно напоминают подобие раскрытого рта крокодила.
Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.
На обе «тарелки» необходимо выложить определенное количество «котлет».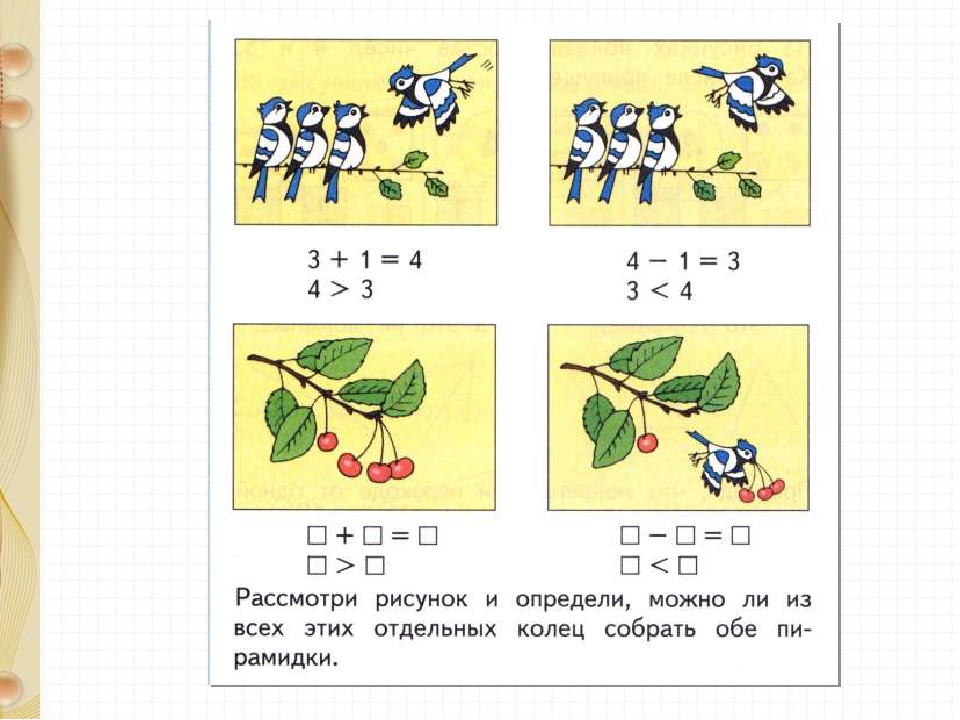
Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «<», а комбинация большого и указательного пальцев правой руки представляет собой символ «>». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Заключение
Итак, в математике обозначения «>» и «<» используются довольно часто. Малыши способны освоить принцип их применения довольно рано. Воспользовавшись советами из этой статьи, родители помогут своим детям сделать это быстро и в увлекательной форме.
Урок математики. (1-й класс): «Знаки «меньше», «больше», «равно»
Цели урока:
- Образовательная: познакомить со знаками меньше «<», больше « >», равно «=» и записями вида 2<3, 3>2, 4=4, повторить геометрический материал, состав чисел;
- Развивающая: развитие коммуникативных качеств личности (умение работать в паре, вести учебный диалог, проводить самооценку)
- Воспитательная: воспитание чувства сопереживания, взаимопомощи.
1. Орг. момент
Внимание, проверь дружок,
Готов ли ты начать урок?
Всёли на месте, всёли в порядке
Книга, ручка и тетрадки?
И цветные карандаши
Ты на парту положи,
И линейку не забудь
В математику держим путь!А сейчас, ребята, поудобнее садитесь,
Не шумите, не вертитесь,
И внимательно считайте
А спрошу вас – отвечайте.
Вам условие понятно?
– Да!
Это слышать мне приятно
Путешествие зовёт
Первоклашек на урок!
2. Основная часть:
Учитель: А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?
Ученики: Решаем, считаем, пишем, думаем…
Учитель: А как вы думаете, что мы будем делать сегодня?
Ученики: Считать, решать, отвечать, думать, чертить…
Учитель: Чтобы полёт прошёл удачно, необходимо быть:
- Внимательными
- Точно и правильно выполнять задания
- Не допускать ошибок, иначе ракета может потерпеть аварию.
В расчётное время, стартуя с Земли,
К загадочным звёздам
Летят корабли
Представим: чуть-чуть помечтали –
И все космонавтами стали.
Учитель: Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)
- Счёт цепочкой до 10.
- Начинает учитель, дети продолжают.
- Отсчёт в обратном направлении.
- Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!
Учитель: Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?
Ученики: геометрические фигуры.
Учитель: Что это за фигуры, назовите.
Ученики: отрезок, прямая, точки, ломаная, кривая.
Учитель: Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.
Рисуй глазами треугольник,
Теперь его переверни
Вершиной вниз
И вновь глазами
Ты по периметру веди.
Рисуй восьмёрку вертикально
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води
И на бочок её клади.
Теперь следи горизонтально.
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец
Зарядка окончилась.
Ты молодец!
Учитель: Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.
1*34**7*910
- Какое число идёт при счёте за числом 3, 6, 9?
- Какое число стоит перед числом 2, 5, 8, 10?
- Назовите соседей числа 2, 7?
Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)
| 2 3=5 | 4 =2 | |
| 5 1=4 | 1+ =4 | |
| 3+ =5 | 5- =4 |
Молодцы! Пульт исправен.
Учитель: Пока наша ракета поднимается ввысь, поиграем в игру «Сложи фигуру».
Нужно из палочек сложить фигуру, состоящую из четырёх квадратов.
Посчитай сколько здесь квадратов? (фигура состоит из 4 квадратов)
Переложи 2 палочки так, чтобы получилось 5 одинаковых квадратов.
Наша ракета всё дальше и дальше удаляется от Земли, как приятно вспомнить всё, что связано с землёй. Представьте, что мы на большой лесной полянке.
Физминутка: (негромко звучит весёлая музыка)
На зарядку солнышко поднимает нас,
Поднимаем руки мы по команде раз,
А над нами весело шелестит листва,
Опускаем руки мы по команде два.
Соберём в корзину ягоды, грибы –
Дружно наклоняемся по команде три.
На четыре и на пять
Будем дружно мы скакать.
Ну, а по команде шесть
Всем за парты тихо сесть!
Учитель: А сейчас приготовьте свои квадраты.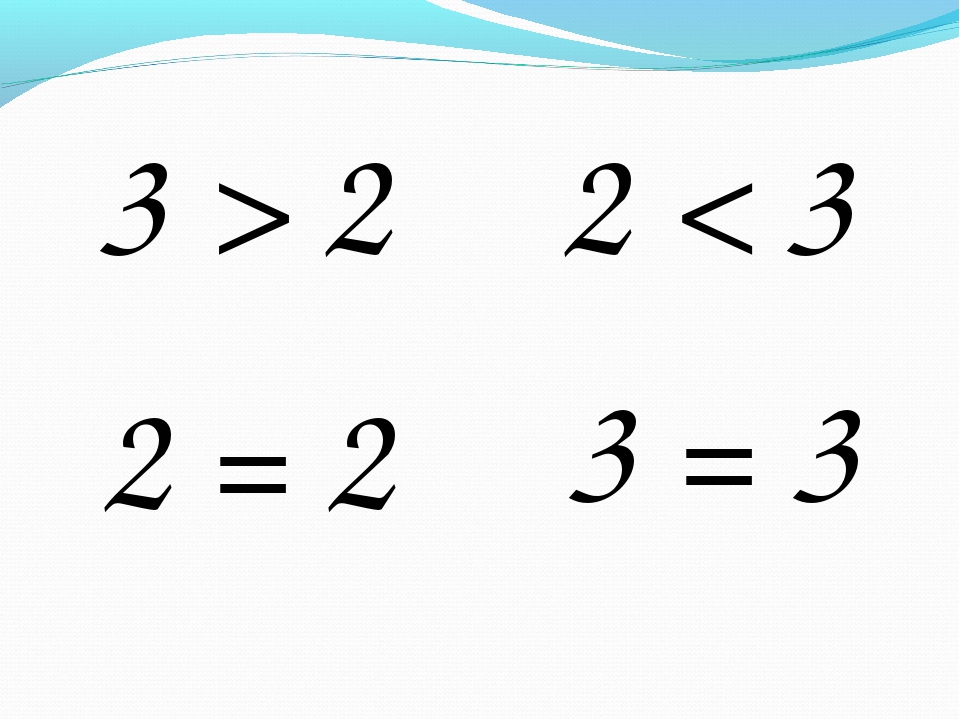 Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.
Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.
Каких квадратов меньше?
Какое число меньше 2 или 3?
В математике есть специальная запись. Это записывают так: 2<3
< – знак меньше
Каких квадратов больше? (синих)
Какое число больше? (3)
Кто догадался, как это записать? 3>2
> – знак больше
Знак ставится так, чтобы к большему числу «клювик» был открыт.
Давайте отдохнём и посмотрим телевизор, что у нас сегодня показывают (работа с учебником, выполнение задания).
- Сколько было птичек на первой картинке
- Сколько прилетело
- Сколько стало
- Их стало больше или меньше
- Как это записали, прочитайте
- Сколько ягод на кисточке
- Что произошло с ягодами
- Как это записать
- Какое число больше, меньше?
Учитель: Наша ракета стремительно несётся ввысь. Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.
Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.
У кого можно попросить помощи, если очень трудно? (соседа по парте)
| 2+2 | 1+2 | 4-2 | ||
| 3+2 | 3-1 | 5-3 |
– Мы победили, корабль удаляется. Заполним ботржурналы. Проверьте рабочее место, сядьте поудобнее, чтобы бортжурналы лежали правильно, записи были чёткими и аккуратными.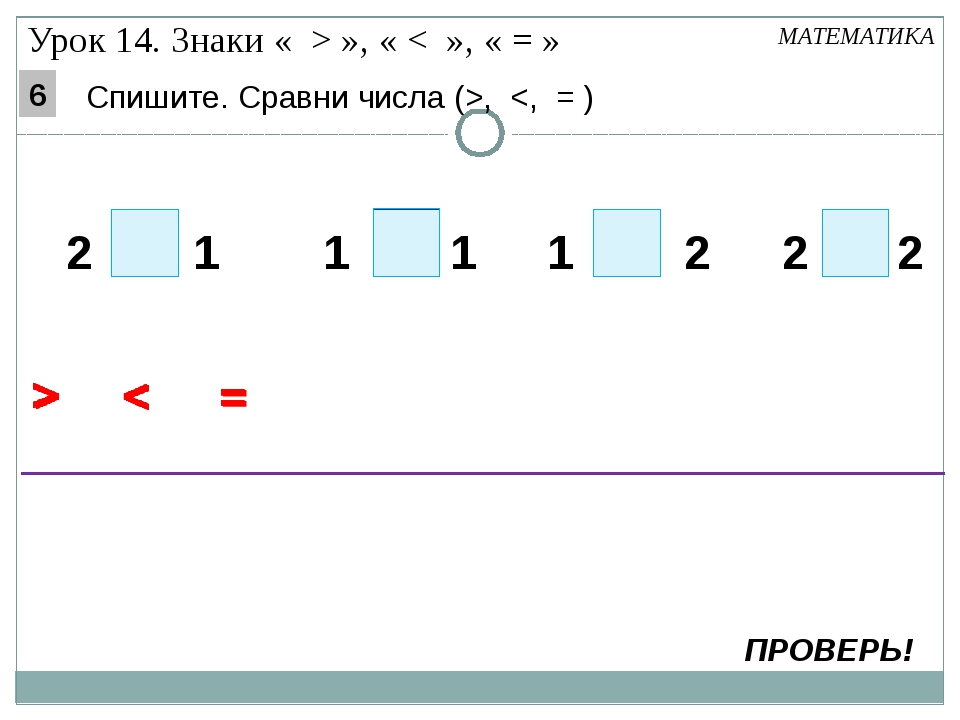 Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)
Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)
– Перед вами знаки. Как называется первый знак? (больше)
Как называется второй знак? (меньше)
Напишите знак по точкам, допишите до конца строки.
Учитель: Перед стартом ракеты я предлагаю вам поработать в паре. У вас на столах карточки, нужно вставить недостающие знаки «больше» или «меньше».
Карточка.
| 2*3 | 5*7 | 8*5 | ||
| 5*3 | 10*7 | 6*2 | ||
| 3*9 | 7*1 | 6*9 |
3.
 Рефлексия:
Рефлексия:Благодаря дружной работе наша ракета совершила мягкую посадку. Во время полёта мы провели большую работу.
– Скажите, что вы для себя узнали нового?
– Чем мы сегодня занимались?
– Что вам помогло хорошо работать на уроке?
У вас на столах лежат мордочки, нарисуйте на них выражения лица весёлое или грустное, кому на уроке было хорошо поднимите весёлую мордочку. А у кого что-то не получилось и было грустно? (таких может не быть)
Полёт завершён, всем спасибо!
ЗНАКИ СРАВНЕНИЯ «БОЛЬШЕ», «МЕНЬШЕ», «РАВНО» | План-конспект урока по математике (1 класс) на тему:
ЗНАКИ СРАВНЕНИЯ «БОЛЬШЕ», «МЕНЬШЕ», «РАВНО»
Педагогические цели: создать условия для ознакомления со знаками сравнения «больше», «меньше», «равно»; развития навыков счёта; закрепления знаний состава изученных чисел; учить писать знаки сравнения «больше», «меньше»; прививать аккуратность.
Планируемые результаты (предметные): знать названия и последовательность чисел от 1 до 5; использовать при сравнении чисел знаки сравнения «больше», «меньше», «равно».
Универсальные учебные действия (метапредметные):
Познавательные: стремиться к расширению своей познавательной сферы, стараться производить логические мыслительные операции (анализ, сравнение) для решения познавательной задачи.
Регулятивные: уметь оценивать результат своей работы на уроке.
Коммуникативные: уметь участвовать в диалоге на уроке и в жизненных ситуациях; отвечать на вопросы учителя, товарищей по классу; соблюдать простейшие нормы речевого этикета: здороваться, прощаться, благодарить; слушать и понимать речь других; осуществлять работу в паре.
Личностные: совместно договариваются о правилах общения и поведения в школе и следуют им; проявляют интерес к новому материалу, касающемуся конкретных фактов, но не теории (учебно-познавательный интерес на уровне реакции на новизну).
Ход урока
I. Устный счёт.
– Назовите соседа.
3 2 4
– Назовите число, которое:
следует за числом 1; на 1 больше числа 3;
предшествует числу 5; на 1 меньше числа 2.
Целесообразнее, чтобы на данном этапе урока ученики пользовались карточками с цифрами.
II. Закрепление состава изученных чисел.
Для проведения этой работы учитель может использовать задание 1 (с. 46 учебника), а также воспользоваться счётным материалом и наборным полотном.
Выполняя задание учебника и пользуясь рисунками и данными равенствами, ученики рассказывают, как можно получить число 5.
Затем, пользуясь различными фигурками счётного материала и наборным полотном, дети составляют разными способами числа 4, 3.
III. Изучение нового материала.
1. Знакомство со знаками сравнения.
– Используя наборное полотно, сравните группы различных предметов.
Например: 5 зайчиков и 4 лисички;
2 розы и 3 ромашки и т. д.
– Можно ли то, что вы сказали, записать?
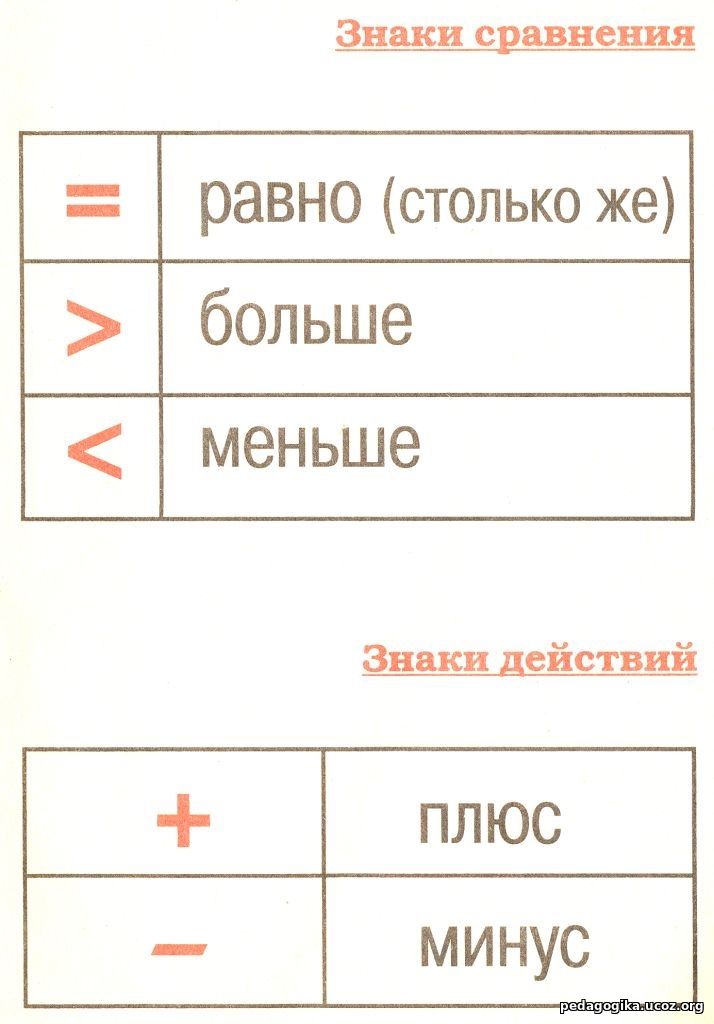
– В математике существуют специальные знаки. Для того чтобы показать, что одно число больше другого, используют знак «больше» (>), а для того чтобы показать, что одно число меньше другого, используют знак «меньше» ().
2. Пропись знаков сравнения.
Учитель показывает учащимся, как правильно писать знаки сравнения «больше», «меньше», и ученики прописывают их в тетрадях (задание 2, с. 18).
Далее на наборное полотно выставляется равное количество каких-либо предметов, например: 3 груши и 3 яблока.
– Сравните количество груш и яблок.
– Как бы вы записали, что количество груш и яблок одинаково?
Учащиеся могут сами предложить использовать знак «равно» (=) в данной записи.
IV. Составление и чтение равенств и неравенств.
Учащиеся, используя рисунки заданий 1, 2 учебника (с. 46), под руководством учителя составляют и читают неравенства и равенства (хором).
Например:
«На ветке сидело 3 птички, к ним прилетела ещё одна. Стало 4 птички. К 3 прибавить 1 получится 4.Четыре больше трёх.
На ветке сидело 4 птички, одна улетела, осталось 3 птички. Из 4 вычесть 1 получится 3. Три меньше четырёх». И т. д.
V. Работа над составом числа 5.
В заключение урока учитель может предложить задание на развитие логического мышления. Например, задание, данное на полях учебника (с. 47).
Например, задание, данное на полях учебника (с. 47).
VI. Итог урока.
Вопросы: Что нового узнали на уроке? Какое задание особенно понравилось?
Знаки больше и меньше в математике — сравнение чисел с примерами
Знаки больше и меньше в математике становятся известны детям еще до поступления в первый класс. Часто детки путают, что означает конкретный символ. Родители могут помочь своим чадам в этом вопросе, что положительно повлияет на успеваемость детей. Эти знания пригодятся малышам и в будущем – при изучении геометрии, на уроках алгебры, в примерах, где используется квадратная, а также другая степень чисел. Советы из дан статьи помогут родителям научить малышей важной математической премудрости.
Математические знаки в картинках для дошкольников
Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.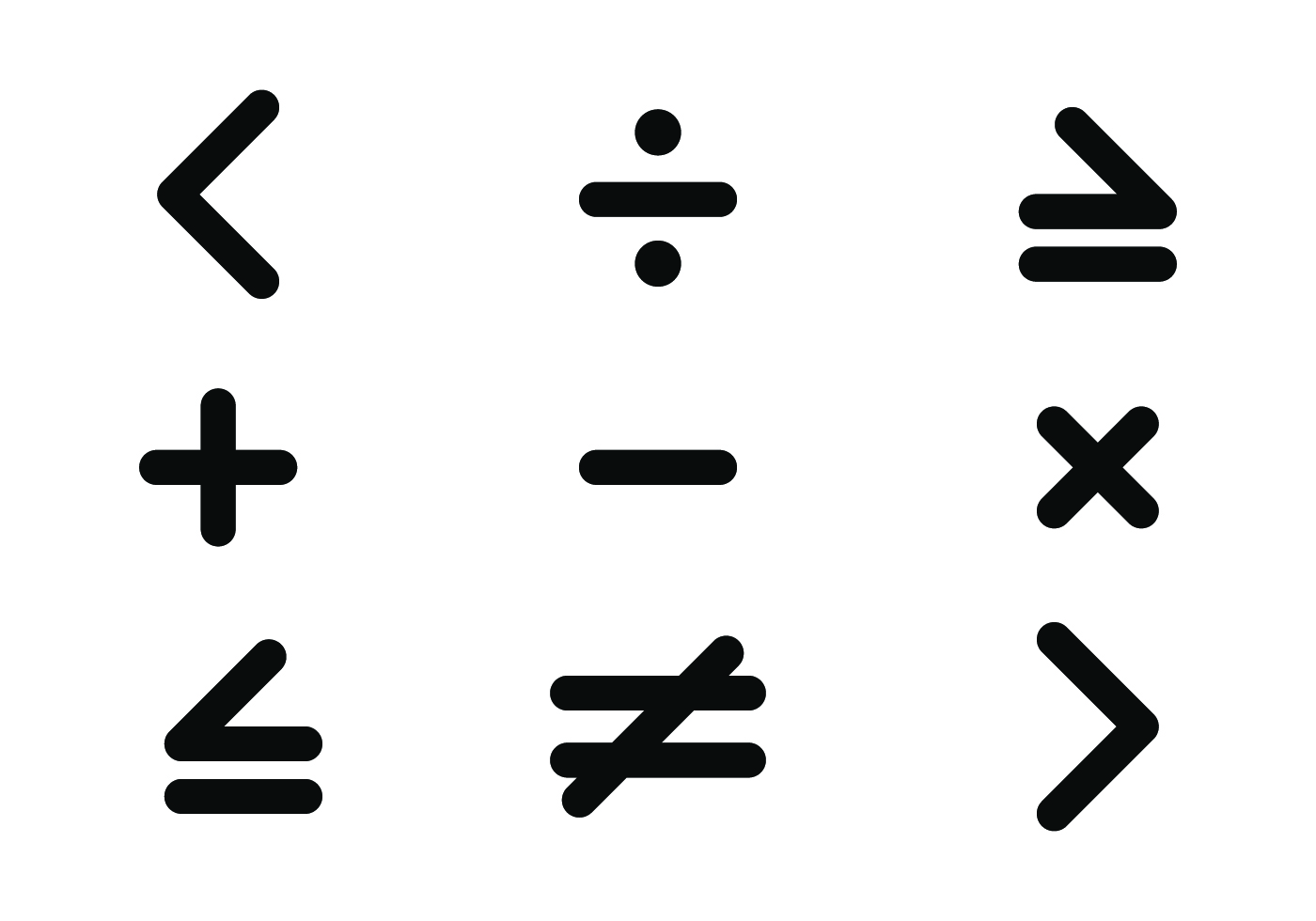
Знак «больше» – в какую сторону
Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».
Знак «меньше» – как правильно писать
Знак «меньше» выглядит так «<». Если сказать просто, то стрелка должна смотреть влево. И снова для определения важна левая часть стрелки. Если точка, из которой выходят две линии, расположена слева, то это символ «<».
Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «<» и одной линии.
Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.
Примеры на сравнение чисел для 1 класса
В первом блоке примеров (Таблица 1) нужно поставить правильный символ. Справа и слева стоят только однозначные числа.
Второй блок примеров (Таблица 2) содержит примеры, в которых нужно сопоставить суммы чисел. В случае равенства необходимо вписать знак «равно».
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «<» примерно напоминают подобие раскрытого рта крокодила.
Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.
На обе «тарелки» необходимо выложить определенное количество «котлет». Затем пусть ребенок положит карточку так, чтобы «рот крокодила» был обращен в сторону «тарелки» на которой больше «котлет».
Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «<», а комбинация большого и указательного пальцев правой руки представляет собой символ «>». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Заключение
Итак, в математике обозначения «>» и «<» используются довольно часто. Малыши способны освоить принцип их применения довольно рано. Воспользовавшись советами из этой статьи, родители помогут своим детям сделать это быстро и в увлекательной форме.
Предыдущая
МатематикаМетод симплекса для чайников — описание с примером подробного решения
СледующаяМатематикаСтаринные меры длины — таблицы и примеры использования в современной системе
Равно, меньше и больше символов
lo1kvxu-Dc8
Помимо знакомого знака равенства (=), он также очень полезен, чтобы показать, не равно ли что-то (≠) больше чем (>) или менее (<)
Это важные знаки, которые необходимо знать :
| = | Когда два значения равны | пример: 2 + 2 = 4 |
| ≠ | Когда два значения определенно равны , а не , равны | пример: 2 + 2 ≠ 9 |
| < | Когда одно значение меньше другого | пример: 3 <5 |
| > | Когда одно значение больше другого | пример: 9> 6 |
Меньше и больше
Знаки «меньше» и «больше» выглядят как буква «V» на своей стороне, не так ли?
Чтобы запомнить, в какую сторону идут знаки «<» и «>», просто запомните:
«Маленький» конец всегда указывает на меньшее число, например:Символ больше, чем: БОЛЬШОЙ> маленький
Пример:
10> 5
«10 больше 5″
Или наоборот:
5 <10
«5 — меньше 10″
Вы видите, как символ «указывает» на меньшее значение?
.
 .. Или равно …
.. Или равно …Иногда мы знаем, что значение меньше, но также может быть равно !
Например, кувшин вмещает до 4 чашек воды.
Так сколько в нем воды?
Это может быть 4 чашки или меньше 4 чашек: Итак, пока мы не измерим, все, что мы можем сказать, «меньше или равно » 4 чашки.
Чтобы показать это, мы добавляем дополнительную строку внизу символа «меньше чем» или «больше чем», например:
Знак «меньше или равно »: | ≤ | |
Знак «больше или равно «: | ≥ |
Все символы
Вот краткое изложение всех символов:
Символ | слов | Пример использования |
|---|---|---|
= | равно | 1 + 1 = 2 |
≠ | не равно | 1 + 1 ≠ 1 |
| | | |
> | больше | 5> 2 |
< | менее | 7 <9 |
| | | |
≥ | больше или равно | мрамора ≥ 1 |
≤ | меньше или равно | собаки ≤ 3 |
Зачем они нужны?
Потому что есть вещи, которые мы не знаем точно. ..
..
… но все же может сказать что-то о .
Итак, у нас есть способы сказать то, что мы знаем (что может быть полезно!)
Пример: у Джона было 10 шариков, но он потерял несколько. Сколько у него сейчас?
Ответ: У него должно быть меньше 10:
Шарики < 10
Если у Джона все еще есть шарики, мы также можем сказать, что у него больше нуля шариков:
Мрамора > 0
Но если бы мы думали, что Джон мог иметь потерять всех своих шариков, мы бы сказали
Мрамора ≥ 0
Другими словами, количество шариков больше или равно нулю.
Объединение
Иногда мы можем сказать две (или более) вещи в одной строке:
Пример: Бекки начинает с 10 долларов, что-то покупает и говорит: «У меня тоже есть сдача». Сколько она потратила?
Ответ: Что-то больше, чем 0 долларов США, но меньше 10 долларов США (но НЕ 0 или 10 долларов США):
«На что тратит Бекки»> 0 долларов
«На что тратит Бекки» <10
Это можно записать одной строкой:
$ 0 <"Сколько тратит Бекки" <10 $
Это говорит о том, что 0 долларов меньше, чем «То, что Бекки тратит» (другими словами, «То, что Бекки тратит» больше, чем 0 долларов), а то, что Бекки тратит, также меньше 10 долларов.
Обратите внимание на то, что «>» перевернулось на «<", когда мы поставили перед , что тратит Бекки. Всегда проверяйте малый конец указывает на малое значение .
Смена сторон
В предыдущем примере мы видели, что когда мы меняем стороны, мы также переворачиваем символ.
| Это: | Бекки тратит> $ 0 | (Бекки тратит более $ 0) | ||
| то же самое, что это: | $ 0 <Бекки тратит | (0 долларов меньше, чем тратит Бекки) |
Просто убедитесь, что маленький конец указывает на маленькое значение!
Вот еще один пример использования «≥» и «≤»:
Пример: у Бекки 10 долларов, и она идет за покупками.
 Сколько она потратит (без использования кредита)?
Сколько она потратит (без использования кредита)?Ответ: Что-то большее или возможное равное 0 долларов США и меньшее или, возможно, равное 10 долларам США:
Бекки тратит ≥ 0 долларов
Бекки тратит ≤ 10 долларов
Это можно записать одной строкой:
0 долл. США ≤ Бекки тратит ≤ 10 долл. США 900 10
Длинный пример: перерезание каната
Вот интересный пример, о котором я подумал:
Пример: Сэм разрезает 10-метровую веревку на две части.Какова длина более длинного куска? Какова длина более короткого отрезка?
Ответ: Назовем длиннее длины веревки « L », а меньшей длины « S »
.L должно быть больше 0 м (иначе это не кусок веревки), а также меньше 10 м:
L> 0
L <10
Итак:
0
Это говорит о том, что L (большая длина веревки) находится между 0 и 10 (но не 0 или 10)
То же самое можно сказать и о более короткой длине « S »:
0
Но я сказал, что есть «короче» и «длиннее», поэтому мы также знаем:
S
(Вы видите, насколько изящна математика? Вместо того, чтобы говорить «меньшая длина меньше, чем большая длина», мы можем просто написать « S
Мы можем объединить все это так:
0
Это говорит о многом:
0 меньше короткой длины, короткой длины меньше длинной, длинной меньше 10.
Если читать «задом наперед», то можно увидеть:
10 больше длинной длины, длинная длина больше короткой длины, короткая длина больше 0.
Это также позволяет нам увидеть, что «S» меньше 10 («перепрыгивая» через «L»), и даже что 0 <10 (что мы все равно знаем), все в одном операторе.
ТЕПЕРЬ у меня есть еще одна хитрость. Если бы Сэм очень постарался, он мог бы разрезать веревку ТОЧНО пополам, так что каждая половина составляет 5 м, но мы знаем, что он этого не сделал, потому что мы сказали, что есть «короче» и «длиннее» длина, поэтому мы также знаем:
S <5
и
L> 5
Мы можем вставить это в нашу очень аккуратную формулировку здесь:
0
И ЕСЛИ мы думали, что две длины МОГУТ быть ровно 5, мы могли бы изменить это на
0 Пример использования алгебры
Хорошо, этот пример может быть сложным, если вы не знаете алгебру, но я подумал, что вы все равно можете его увидеть:
Пример: что такое x + 3, если мы знаем, что x больше 11?
Если x> 11, , то x + 3> 14
(Представьте, что «x» — это количество людей на вашей вечеринке. Если на вашей вечеринке более 11 человек, а прибывают еще 3, значит, сейчас на вашей вечеринке должно быть более 14 человек.)
Если на вашей вечеринке более 11 человек, а прибывают еще 3, значит, сейчас на вашей вечеринке должно быть более 14 человек.)
5250, 5251, 5252, 5253, 5254, 5255, 5256, 5257, 5258, 5259
Запоминание знаков «больше, чем» и знаков «меньше»
Вы помните, как в школе изучали маленькие боковые указатели, похожие на маленькие наконечники стрел:
<>
Многие из нас знают, что эти знаки означают «больше чем» и «меньше чем», но, похоже, не могут вспомнить, какой знак какой.
Но сначала, что означают эти знаки?
Эти знаки используются, когда математические задачи не имеют однозначного ответа, что также называется неравенством. Неравенства сравнивают две вещи, показывая взаимосвязь между ними. Слово «неравенство» означает, что две вещи не равны.
Два знака <и> — это знаки, которые используются, когда вы сравниваете две вещи в математике. В математике вам обычно приходится решать задачу, но при использовании знаков «больше» и «меньше» вы показываете, является ли число больше или меньше другого числа, а не решаете проблему.
Какой знак какой?
Символ> означает «больше». Он показывает, что одно число или значение больше другого числа. Например: 5> 2
Если вы видите символ <, это означает, что одно число меньше другого. Для экзамена: 2 <6
Символы выглядят одинаково, и их легко спутать, выбрав какой символ.
Открытые концы
Самый простой способ запомнить, что за символ — это запомнить, что открытый конец символа всегда обращен к большему числу, а стрелка указывает на маленькое число.
Метод аллигатора
Еще один способ запомнить знаки «больше» и «меньше» — это то, что вы, возможно, помните еще в начальной школе: метод аллигатора.
Представьте себе символы в виде пасти аллигатора с цифрами на каждой стороне, изображающими рыбку. Аллигатор всегда захочет съесть большее количество рыбы. Какое бы число ни было больше, пасть аллигатора открывается навстречу этому числу.
Если бы вам дали 5 и 8 и попросили показать, какое число больше или меньше, аллигатор откроет пасть в сторону 8.Это показывает, что 5 меньше 8.
То же самое могло бы работать, если бы вам дали 10 и 4. Рот аллигатора открылся бы к 10, показывая, что 10 больше, чем 4.
L Метод
Знак «Меньше» начинается с буквы L. Знак «Меньше» также выглядит как L, а знак «больше»> — нет. Так как знак «больше» не похож на букву L, он никогда не может быть «меньше».
Дополнительные советы и видео по основам математики
2 уловки для запоминания знаков «больше» и «меньше»
Что означают эти маленькие символы в каратах, расположенные сбоку? Это неравенство! С неравенством трудно справиться, особенно потому, что знаки «больше чем» и «меньше чем» выглядят очень похожими.Но эти символы очень полезны, потому что они помогают нам показать взаимосвязь между числами или уравнениями таким образом, чтобы не просто сказать, что они равны.
Незнание того, что означают знаки, может сделать домашнее задание по математике примерно таким.
Для чего знаки больше и меньше?
Неравенства — это математические задачи, которые нельзя решить с помощью однозначного «равного» ответа. Вместо этого они сравнивают две вещи, демонстрируя взаимосвязь между ними, а не показывая, что один равен другому .Отсюда и название; «Неравенство» означает, что две вещи не равны.
Все мы знакомы со знаком «=» в математике на этом этапе. Но «>» и «<» встречаются не так часто, не говоря уже о «≥» и «≤».
Вот таблица, охватывающая все символы неравенства :
Символ | Значение |
< | Меньше чем — число слева на меньше, чем справа; 2 <3 |
> | Больше чем — число слева на больше, чем число справа; 3> 2 |
≤ | Меньше или равно — число слева на меньше или равно числа справа; 2 или 3 ≤ 3 |
≥ | Больше или равно — число слева на больше или равно числа справа; 2 или 3 ≥ 2 |
≠ | Не равно — число слева не равно числу справа; 2 ≠ 3 |
Теперь мы наконец поговорим о том, почему на всех этих фотографиях изображены крокодилы.
Как запоминать знаки «больше» и «меньше»
Хотя знаки «больше» и «меньше» имеют четкое значение, их бывает трудно запомнить. Все они похожи, за исключением знака «не равно». Так как же их запомнить?
Метод аллигатора
Один из лучших способов запомнить знаки «больше» и «меньше» — это представить их в виде маленьких аллигаторов (или крокодилов) с числами на каждой стороне, представляющими количество рыб. Аллигатор всегда хочет съесть большее количество рыбы, поэтому , какое бы число ни открывалось, это большее число .
Пасть аллигатора открыта в сторону цифры 4, поэтому даже если бы мы не были уверены, что 4 больше, чем 3, знак> сказал бы нам. Все знаки неравенства показывают соотношение между первым числом и вторым, начиная с первого числа, поэтому 4> 3 переводится как «4 — это больше, чем 3.”
Это работает и наоборот. Если вы видите 5 <8, представьте знак <как маленькую пасть аллигатора, которая собирается жевать какую-то рыбу.
Если вы видите 5 <8, представьте знак <как маленькую пасть аллигатора, которая собирается жевать какую-то рыбу.
Рот направлен на 8, что означает, что 8 больше 5. Знак всегда говорит нам о соотношении между первым числом и вторым, поэтому 5 <8 можно перевести как «5 на меньше . 8. ”
Когда вы работаете с неравенством, вы можете даже нарисовать маленькие глазки на символах, чтобы запомнить, что означает что.Их может быть сложно запомнить, поэтому не бойтесь проявить немного творчества, пока вы действительно не запомните их!
Немного поверните знак «меньше», и вы получите L для «меньше!».
L Метод
Этот метод довольно прост — «меньше» начинается с буквы L, поэтому символ, который больше всего похож на L, означает «меньше чем».
<больше похож на L, чем на>, поэтому <означает «меньше чем. Поскольку> не выглядит как L, он не может быть «меньше чем».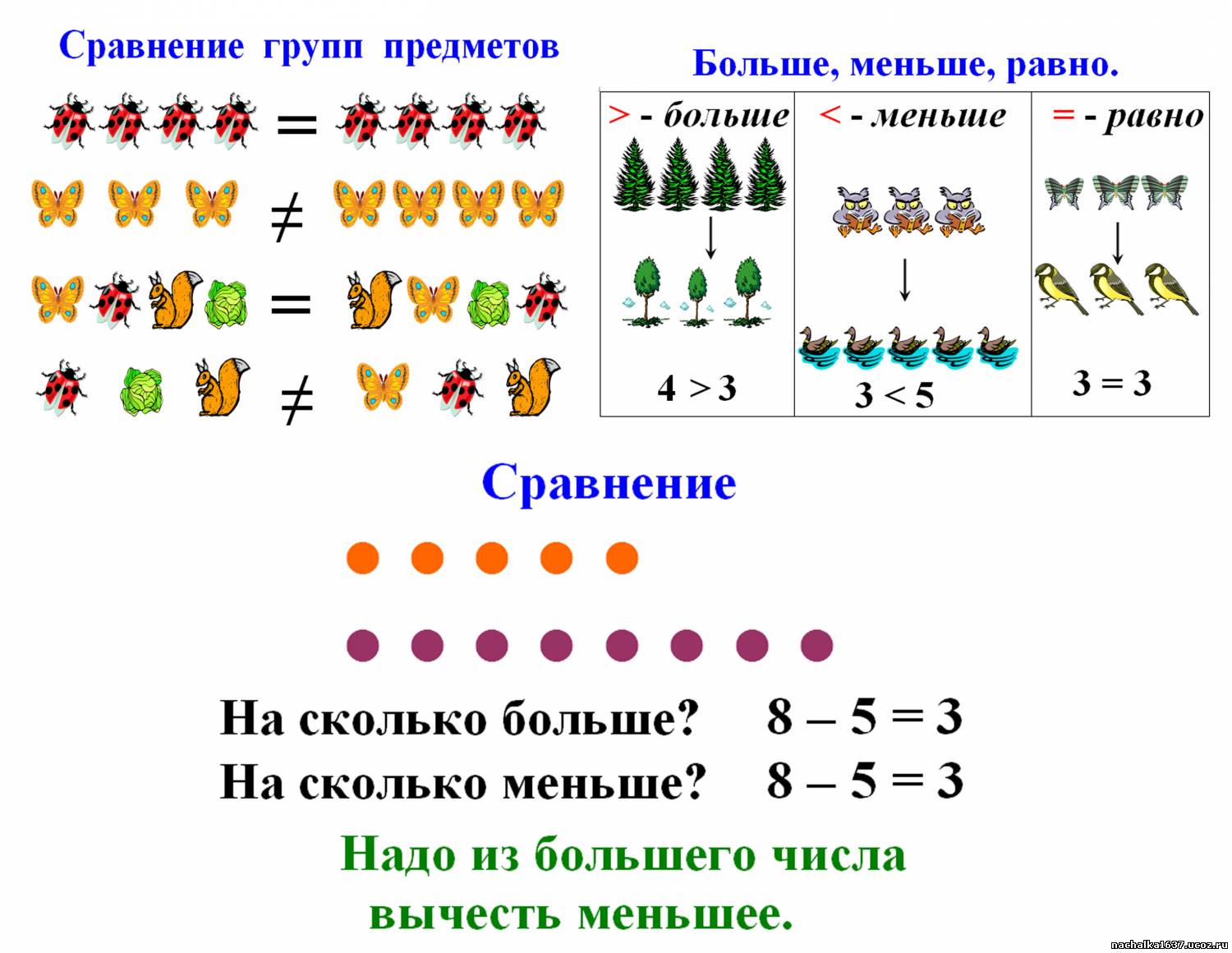
Метод знака равенства
Как только вы освоите метод Аллигатора или L, другие символы станут легкими! «Больше или равно» и «меньше или равно» — это просто применимый символ с половиной знака равенства под ним. Например, 4 или 3 ≥ 1 показывает нам больший знак над половиной знака равенства, что означает, что 4 или 3 на больше или равны 1.
Работает и наоборот.1 ≤ 2 или 3 показывает нам знак «меньше» над половиной знака равенства, поэтому мы знаем, что это означает, что 1 на меньше или равно 2 или 3.
Знак «не равно» еще проще! Это просто зачеркнутый знак равенства. Если вы видите перечеркнутый знак равенства, это означает, что знак равенства не применяется. Таким образом, 2 ≠ 3 означает, что 2 не равно 3.
Помните об этом, и вы будете так счастливы, работая с неравенством.
Ключевые советы по работе с неравенствами
Неравенство — дело сложное — мы привыкли иметь ясный и конкретный ответ на математические задачи, но неравенство не всегда дает нам это. Когда вы работаете с неравенством, помните об этом, чтобы облегчить вам процесс.
Когда вы работаете с неравенством, помните об этом, чтобы облегчить вам процесс.
Неравенство — это все о взаимоотношениях
Имейте в виду, когда вы работаете с неравенствами, они обычно просят вас решить для отношений или определить, какой символ подходит , вместо того, чтобы просить вас решить для одного числа.Чтобы быть правым, не обязательно, чтобы по обе стороны от знака равенства было два числа — просто ответ должен быть правдой.
Изолируйте свои переменные
Когда вы работаете с неравенствами с переменными, важно помнить, что, как правило, вы будете пытаться изолировать переменную с той или иной стороны. Сосредоточьтесь на сжатии чисел и исключении вещей, когда это возможно, всегда с целью получить одну переменную по обе стороны от уравнения.
Отрицательные числа изменяют знак «больше» или «меньше»
Не забывайте, что выполнение определенных действий меняет знак. Когда вы умножаете или делите на отрицательное число, вам нужно перевернуть знак «больше» или «меньше» вместе с ним.
Когда вы умножаете или делите на отрицательное число, вам нужно перевернуть знак «больше» или «меньше» вместе с ним.
Не умножайте и не делите на переменную — в большинстве случаев
Если вы точно не знаете, что переменная всегда будет положительной или всегда отрицательной, не умножает и не делит неравенство на переменную .
Что дальше?
Неравенства — не единственная сложная часть математики — рациональные числа также могут сбивать с толку! Это руководство поможет вам понять, что такое рациональные числа и как они выглядят.
Вы когда-нибудь задумывались, сколько нулей в больших числах? Сколько нулей в миллиард? Как насчет триллиона?
Нужно попрактиковаться? Эти математические игры для 5-х классов помогут тебе отточить свои навыки!
Знаки больше и меньше
В этом уроке мы сравниваем числа и пишем символы сравнения между числами, чтобы показать, какое число больше.
Символ «больше чем» — «>».
Символ «меньше чем» — » Чтобы запомнить, какой знак использовать, этот символ будет указывать на меньшее число, как стрелка.
Другой способ запомнить знаки больше или меньше — это то, что открытый конец символа будет обращен к большему числу. Мы можем представить себе такой символ, как открытый рот крокодила, а затем вспомнить, что крокодил захочет съесть как можно больше, чтобы съесть побольше.
В этом уроке мы напишем символы сравнения «больше чем» и «меньше чем» для сравнения двух чисел.
Мы начнем с нашего первого символа сравнения, равно знаку .
Знак равенства означает «то же значение, что и».
Например:
3 + 1 = 4
4 = 4
Это говорит нам о том, что 3 + 1 имеет то же значение, что и четыре.
Знак «больше» означает «больше» или «больше».
Например:
5> 4
Мы читаем это как «пять — это больше, чем четыре».
Знак «меньше» означает «меньше».
Например:
4 Это читается как «четыре — это меньше, чем пять».
Мы будем использовать несколько примеров знаков «больше или меньше», чтобы посмотреть, как запомнить направление, в котором нарисованы знаки «больше» и «меньше» при сравнении двух чисел.
Чтобы определить, является ли число больше или меньше другого числа, мы можем посмотреть на числовую строку.
Чем дальше мы продвинемся вправо по нашей числовой строке, тем больше будет наше число.
Число больше, чем другого числа, если оно находится правее него в числовой строке.
Больше, чем Пример:
В приведенном ниже примере мы видим, что 3 больше, чем 1. Итак, мы говорим, что тройка на больше, чем единица.
Один из способов запомнить, какой знак ставить между числами, — это думать о знаке сравнения как о стрелке. Эта стрелка указывает на меньшее число.
Итак, он указывает на 1.
Еще один способ запомнить, какой символ больше знака, — представить символ как крокодила.
Крокодил голоден и хочет съесть большее количество. Итак, его пасть открывается в сторону 3.
Меньше, чем Пример:
В приведенном ниже примере мы видим, что 6 меньше 8.
Мы знаем это, потому что 6 находится слева от 8 в числовой строке.
Итак, мы говорим, что шесть меньше восьми.
Мы можем использовать те же два метода, которые использовали ранее, чтобы запомнить, какой знак сравнения представляет «меньше чем».
Думайте о символе как о стрелке, которая всегда указывает на меньшее число. Таким образом, он указывает на 6, а не на 8.
Мы могли бы также думать о знаке «меньше» как о крокодиле, который хочет съесть большее количество. Итак, его пасть открывается в сторону 8.
При обучении знаков больше и меньше самой большой ошибкой является неправильное написание символов.
К счастью, знаки одинаковой формы, только в обратном направлении.
Лучший способ запомнить направление — это то, что знак будет указывать на наименьшее число, например стрелку.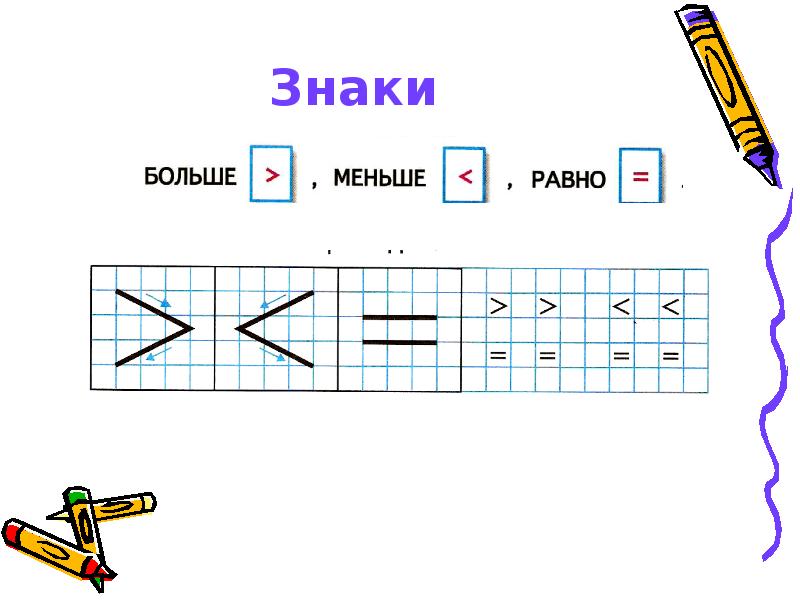
Знак больше и меньше — Math28
Содержимое
Что такое знак «больше»?Символ « больше » представлен знаком «> », это математический элемент, указывающий, что число слева от знака больше числа справа от него.
9> 5
3> 1
21> 15
Чтобы иметь возможность идентифицировать простым способом, считается, что открытие знака означает, что число больше, в этом случае это будут числа слева, а кончик или закрытие знака указывает, что оно меньше, соответствует номеру справа от знака.
Большой маленькийВажно : отверстие всегда указывает на самый большой элемент, а наконечник или закрытие — на самый маленький.
Как вы читаете знак больше?Чтение очень простое, например:
- 15> 12: пятнадцать больше двенадцати.
- 7> 3: семь больше трех.
- 2> 1: два больше единицы.
Использование символа ≥ указывает на то, что число « больше или равно », это означает, что число слева от знака больше или равно числу слева.
8 ≥ 5
6 ≥ 6
4 ≥ 3
Какой знак меньше?
Символ «меньше» представлен знаком «<», это математический элемент, указывающий, что число слева от знака меньше числа справа от него.
7 <9
10 <11
3 <4
Чтобы иметь возможность идентифицировать простым способом, считается, что кончик или закрытие знака указывает на то, что он меньше, в этом случае это будут числа, которые находятся слева от знака, а открытие знака выражает, что число больше, в данном случае это будут числа справа.
Маленькое большоеВажно : отверстие всегда указывает на самый большой элемент, а наконечник или закрытие — на самый маленький.
Как вы читаете знак «меньше»?Чтение очень простое, например:
- 5 <9 Пять меньше девяти.
- 1 <3 Один меньше трех
- 12 <13: Двенадцать меньше тринадцати
При использовании символа ≤ он указывает, что число « меньше или равно », это означает, что число слева от знака меньше или равно числу справа.
3 ≤ 5
5 ≤ 5
5 ≤ 10
Меньшее или большее число на линии
Когда мы помещаем два числа в строку, число справа больше числа слева.
-3-2-1012345Больше мелкихБольшеИз строки следует:
-1> -22> 1
0 <2
2> 1
Сравнение чисел с десятичной дробью
В этом случае важно знать значение позиции чисел, учитывая, что число слева всегда больше числа справа.
Подробнее о: « Разместите значение ». →
Могут возникнуть следующие ситуации:
- Предполагая, что вы хотите сравнить 0,56 и 0,43, сначала выполняется сравнение наибольшей цифры, которая соответствует 5 десятым в 0,56 и 4 десятых в 0,43, так как 5> 4 следует, что 0,56> 0,43.
- Предполагая, что вы хотите сравнить 13 643 и 4849, сначала выполняется сравнение наибольшей цифры, которая соответствует 1 десятке из 13 643 и 4 единицам из 4849, поскольку десятки являются большими значениями, чем единицы, можно быстро вывести, что 13 643 > 4849.
- Предполагая, что вы хотите сравнить 12 439 и 12 434, путем наблюдения мы видим, что наибольшие цифры равны (1 десять из 12 439 и 1 десять из 12435), поэтому мы переходим к следующей наибольшей цифре, поскольку они снова совпадают. (2 единицы из 12 439 и 2 единицы из 12 434) необходимо продолжать опускание позиции до тех пор, пока не будут найдены другие цифры, в этом случае они находятся в позиции тысячных долей со значением позиции 9 тысячных долей 12 439 и 5 тысячных долей 12 435, так как 9> 5 выводит, что 12,439> 12,434
Некоторые предпочитают проводить сравнение в виде дробей, поэтому необходимо переводить десятичные дроби в дроби.
Подробнее о: « Преобразование десятичных дробей в дроби ». →
Сравнение дробей
Для сравнения дробей желательно иметь все в виде дроби, поэтому для смешанных дробей необходимо выполнить соответствующую операцию по преобразованию в дробь.
Подробнее о: « Смешанные фракции ». →
Сравнение дробей с одинаковым знаменателемКогда дроби имеют одинаковый знаменатель, сравнение очень просто, нужно сравнивать только значения числителя.Например:
Сравниваемые числа — 5 и 8, так как 5 <8, то мы имеем:
Сравнение дробей с разным знаменателемКогда дроби имеют другой знаменатель, необходимо преобразовать дроби в их соответствующий эквивалент, чтобы у вас был тот же знаменатель, чтобы можно было легко провести сравнение. Например:
Необходимо преобразовать в эквивалентные дроби, мы только умножаем числитель на знаменатель противоположной дроби, а также знаменатель на знаменатель.
4 x 2 = 85 x 3 = 15
3 x 2 = 6 Теперь мы должны переставить, учитывая новый знаменатель двух дробей (3 x 2 = 6):
Следовательно, сравнивая значения числителя 8 и 15, мы имеем 8 <15:
, ≤, ≥ — легко
Смотреть
Видео
Старт
Практика
Показать
Рабочие листы
Оцените это видео
Ø 5.0/1 оценок
Вы должны войти в систему, чтобы оценить это видео.
Вау, Спасибо!
Дайте нам свою оценку в Google! Мы были бы счастливы.
Автор
Юджин Ли
Описание
Символы неравенства: <,>, ≤, ≥Символы неравенства — это сокращенное обозначение, используемое для сравнения различных величин. Есть четыре символа неравенства: «больше чем», «меньше чем», «больше или равно» и «меньше или равно».Так, например, предложение «5 больше 2» можно записать как 5> 2. Хороший способ запомнить, какое число больше, — представить каждый символ как рот; рот всегда будет есть большее из двух сравниваемых чисел. Узнайте о символах неравенства, помогая вампиру Кристоферу упаковать максимальное количество припасов, необходимых ему для поездки в Калифорнию. Ссылка на Common Core: CCSS.MATH.CONTENT.6.EE.B.8
Стенограмма
Символы неравенства: <,>, ≤, ≥Вампир Кристофер — гурман, и ему нужна свежая, новая история для его блога: Вампир-вегетарианец.Он работает над новым произведением, поэтому он хочет отправиться в место, где растет его любимый фрукт: красный апельсин. В «Вампедии» он читал, что в Калифорнии растут кровавые апельсины, и это прекрасно, потому что он всегда хотел посетить там подземные сады. Чтобы помочь ему собрать вещи, он использует свои знания символов неравенства . И все его припасы у него в постели? Накидки, проверьте. Гель для волос, проверьте. Кровавый апельсиновый сок, проверьте. Но сколько из этих вещей ему разрешено брать с собой в самолет? Взглянем на числовую линию.
Использование неравенства
Путешествие Кристофера Вампира продлится на меньше, чем 15 дней. Для неравенств с ‘меньше’ мы используем этот знак <. Кроме того, для этой поездки Крис не может взять с собой в самолет больше, чем 1000 мл сока кровавого апельсина. Для неравенств типа « меньше или равно » мы используем этот символ: ≤. Нашему гурману-вампиру также нужно упаковать более 1 бутылки геля для волос, так как он закончился во время последнего отпуска.Нарисуем это на числовой прямой. Для неравенств с «больше чем» мы используем символ « больше ». Также ему нужно упаковать не менее 16 накидок, по одной на каждый день и две на всякий случай. Для неравенств с « не менее » мы используем символ « больше или равно ».
Сводка неравенств — Представьте себе рот
Давайте еще раз посмотрим на различные символы неравенства . Хороший способ запомнить, какое число больше, — представить каждый знак как рот .Рот всегда будет съесть большее из двух сравниваемых чисел. Например, сравним 2 и 4. Так как 2 меньше 4, рот съест 4. Если рот открывается вправо, читается: «a» на меньше, чем «b». Однако, если рот открывается влево, читается: «а» на больше, чем «b». Как мы видели ранее, символы «больше» и «меньше» также можно комбинировать со знаком равенства . Когда мы говорим « столько же, сколько» или «не более », мы имеем в виду «меньше или равно», что означает, что а может быть меньше или равно b.Но когда мы говорим « по крайней мере », мы имеем в виду «больше или равно». Здесь a может быть больше b или равно b. Посмотрим, как вампир Кристофер наслаждается отпуском. О, НЕТ! Нет больше кровавых апельсинов?!? Это может усложнить его отпуск …
ПРОЧИТАЙТЕ БОЛЬШЕСимволы неравенства:
<,>, ≤, ≥ УпражнениеХотели бы вы применить на практике то, что вы только что узнали? Практические задачи для этого видео Символы неравенства: <,>, ≤, ≥ помогут вам попрактиковаться и повторить свои знания.
Объясните символы неравенства.
Подсказки
Здесь вы видите числовую строку для $> 65 $.
$ \ ge ~ $ совпадает с $ ~> ~ $, включая отношение $ ~ = ~ $.
Здесь вы видите числовую строку для $ \ le 55 $.
Обратите внимание на кружок.
Решение
Чтобы различать символы неравенства:
- $ <~ $ для отношения меньше . Вы видите соответствующую числовую строку рядом.Тот факт, что Кристофер проводит в своей поездке на меньше, чем 15 дней, представлен пустым кружком.
- $ \ le $ для отношения меньше или равно . Разница между этим символом и символом $ <$ - это знак $ = $. Это видно по закрашенному кружку.
- $> $ для отношения больше . Аналогично отношению $ <$ соответствующий кружок пуст.
- $ \ ge $ для отношения больше или равно .Он также включает знак $ = $, который может отображаться закрашенным кружком.
Найдите символ, который правильно описывает отношения.
Подсказки
Взгляните на этот пример:
$ 4 $ больше, чем $ 2 $.
Вы можете записать это как $ 4> 2 $.
Или вы можете написать это как $ 2 <4 $.
Не менее означает больше или равно.
Запомните знаки отношения:
- $ <$ меньше
- $ \ le $ меньше или равно
- $> $ больше
- $ \ ge $ больше или равно
Решение
Кристофер уже знает, что его поездка занимает менее 15 дней. Меньше указывает на символ $ <$ - или меньше чем: $ <15 $. Для изображения на числовой прямой вы используете пустой кружок, окружающий 15.
Количество красного апельсина, которое он может взять с собой, ограничено сверху на 1000 ~ мл $, включая это количество. Это указывает на символ $ \ le $ — или меньше или равно: $ \ le 1000 $. Здесь вы используете закрашенный кружок.
Кристофер знает, сколько геля для волос ему нужно. Поэтому он приходит к выводу, что нужно упаковать более одной бутылки геля для волос. Это указывает на $> $ — или больше чем-символ: $> 1 $.Снова вы используете пустой кружок.
И последнее, но по крайней мере, он собирает несколько накидок: по крайней мере, один на каждый день и один запасной, всего 16. По крайней мере указывает на $ \ ge $ — или больше или равно символ: $ \ ge 16 $. Здесь вы используете закрашенный кружок на числовой прямой.
Но что это? Прибыв в сад кроваво-оранжевого цвета, Кристофер обнаруживает табличку: Извините! Никаких кровяных апельсинов.
Определите соответствующее математическое неравенство, соответствующее числовой прямой.
Подсказки
Эта числовая прямая представляет собой неравенство $ x \ le 7 $.
- Стрелка слева указывает на $ <$ или $ \ le $.
- Закрашенный кружок означает меньше или равно.
Эта числовая строка означает $ x> -20 $.
Символ $ \ ge $ можно исключить, так как кружок пустой.
Решение
Сначала рассмотрим числовые прямые в целом.
- Стрелка слева указывает на отношение $ <$ или $ \ le $.
- Стрелка вправо указывает на отношение $> $ или $ \ ge $.
- Пустой кружок означает $ <$ или $> $ в зависимости от направления стрелки.
- Закрашенный кружок означает $ \ le $ или $ \ ge $.
- $ x \ le 8 $
- $ x <8 $
- $ x> 4 $
- $ x \ ge 4 $
Изучите неравенство по разным задачам со словами.
Подсказки
Не менее означает больше или равно.
Более обозначают символ $> $.
Различать меньше чем ($ <$) и меньше или равно ($ \ le $).
Решение
Вы можете запомнить различные ключевые слова, которые указывают на символ неравенства:
- Больше чем означает больше, чем $> $.
- Не менее означает, что $ \ ge $ больше или равно.
День рождения Вы хотите пригласить менее 10 друзей. Получаем $ x <10 $.
Наушники Более обозначают символ $> $. Это дает нам $ x> 25 $.
Решите, какой символ неравенства использовать.
Подсказки
Обратите внимание
Если вы измените знак чисел, вам также придется изменить символ неравенства.Позаботьтесь об использовании $> $ или $ \ ge $:
- $ 7 \ ge 7 $, но $ 7 \ not> 7 $
- $ 7> 4 $ а также $ 7 \ ge 4 $
Решение
Вы можете представить себе символ «больше чем» в виде рта.
Чем большее число съедает, тем большее число.
- Например, $ 4> 2 $. Вы также можете использовать знак $ \ ge $.
- Аналогично $ 2 <4 $, а также $ 2 \ le 4 $. Порядок изменен.
- $ -2> -4 $, а также $ -2 \ ge -4 $.
- И наоборот, мы можем заключить, что $ -4 <-2 $ или $ -4 \ le -2 $.
Определите соответствующее неравенство.
Подсказки
Обратите внимание на кружок:
- Пустые кружки обозначают $> $ или $ <$.
- Закрашенные кружки обозначают $ \ ge $ или $ \ le $.
Кружок указывает число, которое вы должны использовать в неравенстве.
Кружок указывает, с одной стороны, на число 65 долларов США, а с другой — на то, что 65 долларов США принадлежат неравенству.
Стрелка справа указывает $> $ или $ \ ge $.
Вместе мы можем заключить следующее неравенство для этой числовой прямой:
$ x \ ge 65 $.
Решение
Вы используете числовые линии для обозначения неравенства.
Сначала вы рисуете круг точно на месте соответствующего числа.
В зависимости от символа неравенства кружок заполнен или пуст:
- Пусто: $> $ или $ <
- Заполнено: $ \ ge $ или $ \ le $
Здесь вы видите четыре разные числовые линии, сверху вниз:
- $ x> -6 $
- $ х \ ле -2 $
- $ x <4 $
- $ х \ ge 2 $
Больше видео в Решение уравнений
Сравнение чисел (меньше, больше и равно) — по математике для 3-го класса
Научитесь сравнивать числа
🤓 Ознакомьтесь с этими заявлениями.
429 < 835
87 > 61
Вы помните, что означают эти символа ? 🤔
Очень хорошо! 😃
< — это на меньше символа.
> — это больше символа.
👉 Это символа сравнения.
В предыдущих классах вы научились сравнивать чисел.
Давайте рассмотрим это сегодня. 😎
1, 2, 3 и 4-значные номера
Номера могут состоять из 1, 2, 3 и более цифр.
👉 Однозначные числа имеют только цифру в разряде Единицы .
👉 2-значные числа имеют цифры в разрядах Десятки и Единицы .
👉 3-значные числа имеют цифры в разрядах Сотни , Десятки и Единицы разрядов.
👉 4-значные числа имеют цифры в разрядах тысяч , сотен , десятков и единиц разрядов.
Обзор сравнения чисел
Проверка того, какое число больше или меньше, называется при сравнении .
Мы используем символа сравнения (>, <и =) для сравнения чисел.
Вот что означает каждый символ сравнения:
СОВЕТ НА ЗАПОМНИТЬ!
Для больше и меньше символов широко открытая горловина символа всегда обращена на большее число.
Как сравнивать числа
🌟 Чтобы сравнить любые два числа, выполните следующие действия:
Шаг 1: Всегда начинаются с цифр в самой высокой позиции .
Шаг 2: Сравните цифры в этом месте значения в обоих числах.Число с большей цифрой больше.
Шаг 3: Если цифры равны, переместит одно разрядное значение вправо 👉 и повторите Шаг 2.
Давайте рассмотрим эти шаги на нескольких примерах! 🤗
Пример 1
Сравните 46 и 85. Что больше?
Какие цифры мы должны сравнить в первую очередь?
Верно!
✅ Начнем со сравнения цифр в наивысшем значении . Вот это место Десятки .
У какого числа большая цифра? 🤔
Очень хорошо! У 85 есть большая цифра в разряде десятков.
Итак,
46 < 85
__
Попробуем другой пример.
Пример 2Что больше: 2953 или 2953?
😎 Давайте повторим шаги еще раз.
✅ Сначала мы сравниваем цифры в наивысшем значении . Вот, это место Тысячи.
Но подождите! Эти цифры равны. 🤔
Что нам теперь делать?
Вы поняли! 👍
✅ Перемещаем на одну позицию вправо на 👉 и сравниваем цифры в разряде сотен.
Эти цифры тоже совпадают. 🤓
✅ Итак, мы снова перемещаем на одну позицию вправо на 👉 и сравниваем цифры в разряде десятков.
Что ты видишь?
Правильно! Цифры снова равны.🤗
✅ В последний раз мы снова перемещаем на одну позицию вправо на и сравниваем цифры в единичной позиции.
Что ты видишь? 🤔
Все цифры в номерах равны.
Итак,
2,953 = 2,953
Отличная работа! 👏
__
Попробуем еще один пример.
Пример 3Сравните 3,148 и 692.
Давайте еще раз повторим шаги! 🤗
✅ Мы начинаем с цифр наивысшего значения.
Какая здесь самая высокая числовая ценность? 🤓
Очень хорошо! Это числовое значение тысяч .
✅ Поскольку число 692 не имеет цифры в этом значении разряда, мы можем поместить туда ноль (0) .
А теперь сравним!
Что вы видите?
Вы правы!
3148 имеет большую цифру в разряде тысяч.
Итак,
3,148 > 692
Отличная работа! 🎉
Смотри и учись
Теперь вы знаете, как сравнивать числа! 👏 А теперь задайте несколько вопросов.
.
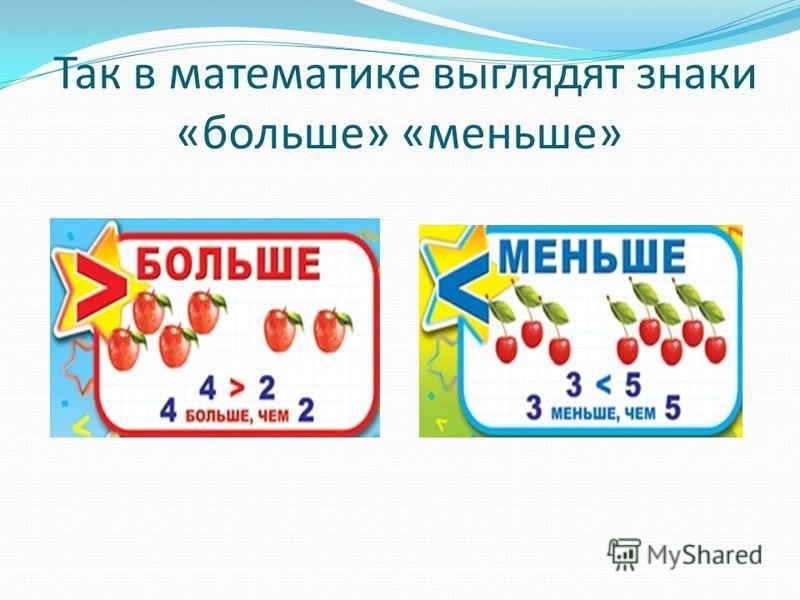 Нарисуйте два круга – две тарелки. Внутри каждой — множества предметов, которые надо сравнить. Рядом напишите знаки «больше» и «меньше». Попросите ребенка представить, что каждый из знаков – рот крокодила, указывающий в определённую сторону. Голодный крокодил наверняка выберет тарелку с большим количеством пищи, поэтому его пасть будет широко открыта возле этой тарелки. Это и есть знак «больше». Можно сравнивать и с клювом птички, если ребенку по душе такое сравнение.
Нарисуйте два круга – две тарелки. Внутри каждой — множества предметов, которые надо сравнить. Рядом напишите знаки «больше» и «меньше». Попросите ребенка представить, что каждый из знаков – рот крокодила, указывающий в определённую сторону. Голодный крокодил наверняка выберет тарелку с большим количеством пищи, поэтому его пасть будет широко открыта возле этой тарелки. Это и есть знак «больше». Можно сравнивать и с клювом птички, если ребенку по душе такое сравнение.